3.4: General Multiplication Probability

Last updated
Save as PDF

Page ID: 25654

Jupei Hsiao
Rio Hondo College

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

\( \newcommand{\Span}{\mathrm{span}}\)

\( \newcommand{\id}{\mathrm{id}}\)

\( \newcommand{\Span}{\mathrm{span}}\)

\( \newcommand{\kernel}{\mathrm{null}\,}\)

\( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\)

\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\)

\( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)

\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)

\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vectorC}[1]{\textbf{#1}} \)

\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)

It is a hot summery day. You are looking forward to an unopened pint of (cow milk based) ice cream that you have waiting for you in the freezer. When you reach for the carton and take off the lid, you see that there are only two spoonfuls left. Who is the ice cream thief in your household?

You live with your family, which consists of your grandma, both two parents, and three siblings; a total of six suspects. At this point, you have a probability of \(\dfrac{1}{6}\) of guessing correctly who is the thief.

However, you know your grandma's gums are sensitive to cold food. Also, one parent and two siblings are lactose intolerant. That leaves only two possible suspects: the other parent and one sibling. At this point, you have a probability of \(\dfrac{1}{2}\) of guessing correctly who is the thief. This is an example of conditional probability, where instead of looking at the entire sample space, we look at a smaller group to find the correct probability.

Conditional Probability

The conditional probability of \(\text{A}\) given \(\text{B}\) is written \(P(\text{A|B})\). \(P(\text{A|B})\) is the probability that event \(\text{A}\) will occur given that the event \(\text{B}\) has already occurred. A conditional reduces the sample space. We calculate the probability of \(\text{A}\) from the reduced sample space \(\text{B}\). The formula to calculate \(P(\text{A|B})\) is

\[P(\text{A|B}) = \frac{\text{P(A AND B)}}{\text{P(B)}} \nonumber\]

where \(P(\text{B})\) is greater than zero.

Although the formula can be intimidating, there are times when we can find conditional probabilities without it.

Example \(\PageIndex{1A}\)

Suppose we toss one fair, six-sided die. The sample space \(\text{S} = \{1, 2, 3, 4, 5, 6\}\). Let event A be rolling a 2 or 3, \(\text{A} =\{2,3\}\). Let event B be rolling an even number, \(\text{B} =\{2,4,6\}\).

What is the probability of getting event A, given we know event B happened? In other words, what is \(P(\text{A|B})\)? Since there three outcomes in event B. Both events A and B only share one outcome, "2". Then \(P(\text{A|B}) = \dfrac{1}{3}.\)

Example \(\PageIndex{1B}\)

Let's do the example above, but with using the formula.

Remember that \(\text{S}\) has six outcomes.

\(P(\text{A|B}) \\= \dfrac{ \text{ P(A AND B) } } {P(\text{B})} \\= \dfrac{\dfrac{\text{the number of outcomes that are 2 or 3 AND even in S}}{6}}{\dfrac{\text{the number of outcomes that are even in S}}{6}} \\= \dfrac{\frac{1}{6}}{\frac{3}{6}} = \dfrac{1}{3}\)

Notice, we get the same answer as in Example 1A.

Notation: \(\text{A|B}\) is equivalent to \(\text{A GIVEN B}\)

Example 3.4.2

A fair, six-sided die is rolled. Describe the sample space S, identify each of the following events with a subset of S and compute its probability (an outcome is the number of dots that show up).

Event \(\text{A} =\) the outcome is an even number.
Event \(\text{B} =\) the outcome is less than four.
\(\text{A GIVEN B}\)
\(\text{B GIVEN A}\)

Answer

\(A = \{2, 4, 6\}\), \(P(\text{A}) = \frac{1}{2}\)
\(\text{B} = \{1, 2, 3\}\), \(P(\text{B}) = \frac{1}{2}\)
\(\text{A|B} = \{2\}\), \(P(\text{A|B}) = \frac{1}{3}\)
\(\text{B|A} = \{2\}\), \(P(\text{B|A}) = \frac{1}{3}\)

With or Without Replacement

Sampling may be done with replacement or without replacement (Figure 3.4.1 ):

With replacement: If each member of a population is replaced after it is picked, then that member has the possibility of being chosen more than once. When sampling is done with replacement, then events are considered to be independent, meaning the result of the first pick will not change the probabilities for the second pick.
Without replacement: When sampling is done without replacement, each member of a population may be chosen only once. In this case, the probabilities for the second pick are affected by the result of the first pick. The events are considered to be dependent or not independent.

alt — Figure 3.4.1 : A visual representation of the sampling process. If the sample items are replaced after each sampling event, then this is "sampling with replacement" if not, then it is "sampling without replacement". (CC BY-SA 4.0; Dan Kernler).

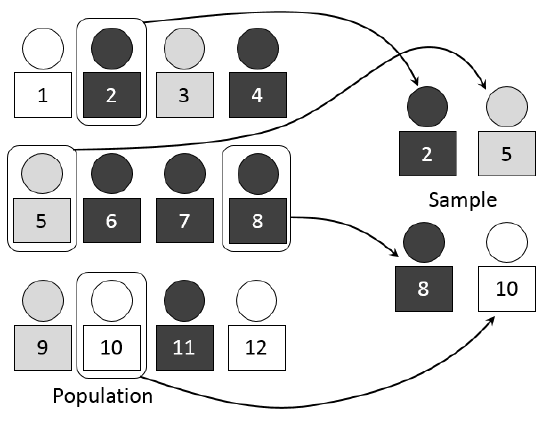
If it is not known whether \(\text{A}\) and \(\text{B}\) are independent or dependent, assume they are dependent until you can show otherwise.

Example 3.4.3

You have a fair, well-shuffled deck of 52 cards. It consists of four suits. The suits are clubs, diamonds, hearts and spades. There are 13 cards in each suit consisting of 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, \(\text{J}\) (jack), \(\text{Q}\) (queen), \(\text{K}\) (king) of that suit.

a. Sampling with replacement:

Suppose you pick three cards with replacement. The first card you pick out of the 52 cards is the \(\text{Q}\) of spades. You put this card back, reshuffle the cards and pick a second card from the 52-card deck. It is the ten of clubs. You put this card back, reshuffle the cards and pick a third card from the 52-card deck. This time, the card is the \(\text{Q}\) of spades again. Each time you drew a card and replaced it before drawing another card is sampling with replacement.

b. Sampling without replacement:

Suppose you pick three cards without replacement. The first card you pick out of the 52 cards is the \(\text{K}\) of hearts. You put this card aside and pick the second card from the 51 cards remaining in the deck. It is the three of diamonds. You put this card aside and pick the third card from the remaining 50 cards in the deck. The third card is the \(\text{J}\) of spades. Each time you drew a card and did not replace it into the deck before drawing another card is sampling without replacement.

Example 3.4.4

Suppose you know that the picked cards are \(\text{Q}\) of spades, \(\text{K}\) of hearts and \(\text{Q}\) of spades. Can you decide if the sampling was with or without replacement?
Suppose you know that the picked cards are \(\text{Q}\) of spades, \(\text{K}\) of hearts, and \(\text{J}\) of spades. Can you decide if the sampling was with or without replacement?

Answer a: With replacement
Answer b: No

Example 3.4.5

You have a fair, well-shuffled deck of 52 cards. It consists of four suits. The suits are clubs, diamonds, hearts, and spades. There are 13 cards in each suit consisting of 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, \(\text{J}\) (jack), \(\text{Q}\) (queen), and \(\text{K}\) (king) of that suit. \(\text{S} =\) spades, \(\text{H} =\) Hearts, \(\text{D} =\) Diamonds, \(\text{C} =\) Clubs.

Suppose you pick four cards, but do not put any cards back into the deck. Your cards are \(\text{QS}, 1\text{D}, 1\text{C}, \text{QD}\).
Suppose you pick four cards and put each card back before you pick the next card. Your cards are \(\text{KH}, 7\text{D}, 6\text{D}, \text{KH}\).

Which of a. or b. did you sample with replacement and which did you sample without replacement?

Answer a: Without replacement
Answer b: With replacement

General Multiplication Rule

In Section 3.3, we learned the Multiplication Rule when events A and B are independent:

\( P( \text{A AND B}) = P(\text{A}) \cdot P(\text{B}) \)

However, if events A and B are dependent, then

\( P( \text{A AND B}) = P(\text{A}) \cdot P(\text{B|A}) \)

Example 3.4.6

A gum ball machine has 5 red balls, 6 green balls, and 5 yellow balls. Suppose you Find the following probabilities.

\(P(\text{draw a red ball and then a green})\) with replacement
\(P(\text{draw a red ball and then a green}) \) without replacement
\(P(\text{draw three red balls}) \) with replacement
\(P(\text{draw three red balls}) \) without replacement
\( P(\text{draw a red ball, two green balls, and one yellow ball} ) \) with replacement
\( P(\text{draw a red ball, two green balls, and one yellow ball} ) \) without replacement

Answer a

\(P(\text{draw a red ball and then a green replacement}) = P(\text{red}) \cdot P(\text{green})= \frac{5}{16} \cdot \frac{6}{16} = 0.1172 \)

Since we are replacing this the ball after each draw, you recover the total number of gumballs each time, which was 16.

Answer b

\(P(\text{draw a red ball and then a green}) = P(\text{red})\cdot P(\text{green})= \frac{5}{16} \cdot \frac{6}{15} = 0.128\)

Since we are not replacing this the ball after each draw, the total number of gumballs each time decreases by one.

Answer c

\(P(\text{draw three red balls}) = P(\text{red})\cdot P(\text{red})\cdot P(\text{red})= \frac{5}{16} \cdot \frac{5}{16} \cdot\ frac{5}{16} = 0.3052\)

Answer d

\(P(\text{draw three red balls}) = P(\text{red}) \cdot P(\text{red}) \cdot P(\text{red})= \frac{5}{16} \cdot \frac{4}{15} \cdot \frac{3}{14} = 0.0179\)

Answer e

\(P(\text{draw a red ball, two green balls, and one yellow ball}) = P(\text{red}) \cdot P(\text{green}) \cdot P(\text{green}) \cdot P(\text{yellow})= \frac{5}{16} \cdot \frac{6}{16} \cdot \frac{6}{16} \cdot \frac{5}{16} = 0.0137\)

Answer f

Glossary

Independent Events: If one event does not affect the other, then the two events are independent.
Dependent Events: If two events are NOT independent, then we say that they are dependent.

Sampling with Replacement: If each member of a population is replaced after it is picked, then that member has the possibility of being chosen more than once.

Sampling without Replacement: When sampling is done without replacement, each member of a population may be chosen only once.

The Conditional Probability of One Event Given Another Event: P(A|B) is the probability that event A will occur given that the event B has already occurred.

Search

Text Color

Text Size

Margin Size

Font Type