2.2: Conditional Probability I
- Page ID
- 326
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Are students more likely to use marijuana when their parents used drugs? The drug use data set contains a sample of 445 cases with two variables, student and parents, and is summarized in Table \(\PageIndex{1}\) The student variable is either uses or not, where a student is labeled as uses if she has recently used marijuana. The parents variable takes the value used if at least one of the parents used drugs, including alcohol.
|
parents |
|||
|---|---|---|---|
| used | not | Total | |
| uses | 125 | 94 | 219 |
| not | 85 | 141 | 226 |
| Total | 210 | 235 | 445 |
| 23Ellis GJ and Stone LH. 1979. Marijuana Use in College: An Evaluation of a Modeling Explanation. Youth and Society 10:323-334. | |||
Example \(\PageIndex{1}\)
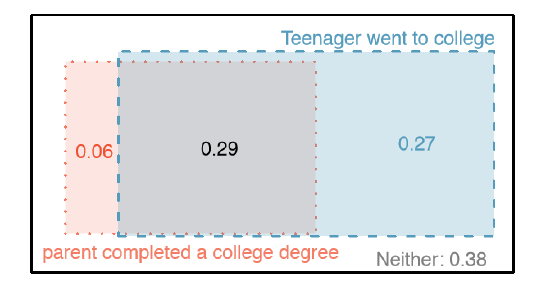
If at least one parent used drugs, what is the chance their child (student) uses?
Solution
We will estimate this probability using the data. Of the 210 cases in this data set where parents = used, 125 represent cases where student = uses:
\[ P (student = uses given parents = used) = \dfrac {125}{210} = 0.60 \]
Exercise \(\PageIndex{1}\)
A student is randomly selected from the study and she does not use drugs. What is the probability that at least one of her parents used?
Solution
If the student does not use drugs, then she is one of the 226 students in the second row. Of these 226 students, 85 had at least one parent who used drugs:
\[ P (parents = used given student = not) = \dfrac {85}{226} = 0.376 \]
Marginal and Joint Probabilities
Table \(\PageIndex{2}\) includes row and column totals for each variable separately in the drug use data set. These totals represent marginal probabilities for the sample, which are the probabilities based on a single variable without conditioning on any other variables. For instance, a probability based solely on the student variable is a marginal probability:
\[ P (student = uses) = \dfrac {219}{445} = 0.492 \]
A probability of outcomes for two or more variables or processes is called a joint probability:
\[ P(student = uses and parents = not) = \dfrac {94}{445} = 0.21 \]
It is common to substitute a comma for "and" in a joint probability, although either is acceptable.
| parents: used | parents: not | Total | |
|---|---|---|---|
| student: uses | 0.28 | 0.21 | 0.49 |
| student: not | 0.19 | 0.32 | 0.51 |
| Total | 0.47 | 0.53 | 1.00 |
| Joint outcome | Probability |
|---|---|
| parents = used, student = uses | 0.28 |
| parents = used, student = not | 0.19 |
| parents = not, student = uses | 0.21 |
| parents = not, student = not | 0.32 |
| Total | 1.00 |
Definition: Marginal and joint probabilities
If a probability is based on a single variable, it is a marginal probability. The probability of outcomes for two or more variables or processes is called a joint probability.
We use table proportions to summarize joint probabilities for the drug use sample. These proportions are computed by dividing each count in Table \(\PageIndex{1}\) by 445 to obtain the proportions in Table \(\PageIndex{1}\). The joint probability distribution of the parents and student variables is shown in Table 2.14.
Exercise \(\PageIndex{1}\)
Verify Table \(\PageIndex{3}\) represents a probability distribution: events are disjoint, all probabilities are non-negative, and the probabilities sum to 1.24
We can compute marginal probabilities using joint probabilities in simple cases. For example, the probability a random student from the study uses drugs is found by summing the outcomes from Table \(\PageIndex{3}\) where student = uses:
\[ P ( \underline {student = uses} )\]
\[= P (parents = used, \underline {student = uses} + P (parent = not, \underline {student = uses}\]
\[ = 0.28 + 0.21 = 0.49 \]
Defining Conditional Probability
There is some connection between drug use of parents and of the student: drug use of one is associated with drug use of the other (This is an observational study and no causal conclusions may be reached). In this section, we discuss how to use information about associations between two variables to improve probability estimation.
The probability that a random student from the study uses drugs is 0.49. Could we update this probability if we knew that this student's parents used drugs? Absolutely. To do so, we limit our view to only those 210 cases where parents used drugs and look at the fraction where the student uses drugs:
\[ P (student = uses given parents = used) = \dfrac {125}{210} = 0.60 \]
24Each of the four outcome combination are disjoint, all probabilities are indeed non-negative, and the sum of the probabilities is 0.28 + 0.19 + 0.21 + 0.32 = 1.00.
We call this a conditional probability because we computed the probability under a condition: parents = used. There are two parts to a conditional probability, the outcome of interest and the condition. It is useful to think of the condition as information we know to be true, and this information usually can be described as a known outcome or event.
We separate the text inside our probability notation into the outcome of interest and the condition:
\[ P (student = uses given parents = used) = P ( student = uses | parents = used ) \label {2.37}\]
\[ = \dfrac {125}{210} = 0.60\]
The vertical bar "|" is read as given.
In Equation \ref{2.37}, we computed the probability a student uses based on the condition that at least one parent used as a fraction:
\[\begin{align} P (student = uses | parents = used) &= \dfrac { \text {# times student = uses given parents = used}}{ \text {# times parents = used}} \label {2.38} \\[5pt] &= \dfrac {125}{210} \\[5pt] &= 0.60 \end{align}\]
We considered only those cases that met the condition, parents = used, and then we computed the ratio of those cases that satis ed our outcome of interest, the student uses.
Counts are not always available for data, and instead only marginal and joint probabilities may be provided. For example, disease rates are commonly listed in percentages rather than in a count format. We would like to be able to compute conditional probabilities even when no counts are available, and we use Equation (2.38) as an example demonstrating this technique.
We considered only those cases that satis ed the condition, parents = used. Of these cases, the conditional probability was the fraction who represented the outcome of interest, student = uses. Suppose we were provided only the information in Table 2.13 on the preceding page ,i. e. only probability data. Then if we took a sample of 1000 people, we would anticipate about 47% or \(0.47 X 1000 =470 \) would meet our information criterion. Similarly, we would expect about 28% or \(0.28 X 1000 = 280 \) to meet both the information criterion and represent our outcome of interest. Thus, the conditional probability could be computed:
\[ P (student = uses | parents = used) = \dfrac { \text {# times student = uses given parents = used}}{ \text {# times parents = used}} \]
\[ \dfrac {280}{470} = \dfrac {0.28}{0.47} = 0.60 \label {2.39}\]
In Equation (2.39), we examine exactly the fraction of two probabilities, 0.28 and 0.47, which we can write as
\[ P (student = uses and parents = used) and P(parents = used) \].
The fraction of these probabilities represents our general formula for conditional probability.
Definition: Conditional Probability
The conditional probability of the outcome of interest A given condition B is computed as the following:
\[ P (A|B) = \dfrac { P (A and B)}{P (B) } \label {2.40}\]
Exercise 2.41 (a)Write out the following statement in conditional probability notation: "The probability a random case has parents = not if it is known that student = not ". Notice that the condition is now based on the student, not the parent. (b) Determine the probability from part (a). Table 2.13 on page 81 may be helpful.26
Exercise 2.42 (a) Determine the probability that one of the parents had used drugs if it is known the student does not use drugs. (b) Using the answers from part (a) and Exercise 2.41(b), compute
\[ P (parents = used | student = not ) + P (parents = not | student = not )\]
(c) Provide an intuitive argument to explain why the sum in (b) is 1.27
Exercise 2.43 The data indicate that drug use of parents and children are associated. Does this mean the drug use of parents causes the drug use of the students?28
Smallpox in Boston, 1721
The smallpox data set provides a sample of 6,224 individuals from the year 1721 who were exposed to smallpox in Boston.29 Doctors at the time believed that inoculation, which involves exposing a person to the disease in a controlled form, could reduce the likelihood of death.
Each case represents one person with two variables: inoculated and result. The variable inoculated takes two levels: yes or no, indicating whether the person was inoculated or not. The variable result has outcomes lived or died. These data are summarized in Tables 2.15 and 2.16.
Exercise 2.44 Write out, in formal notation, the probability a randomly selected person who was not inoculated died from smallpox, and nd this probability.30
26(a) P(parent = notjstudent = not). (b) Equation (2.40) for conditional probability indicates we should rst nd P(parents = not and student = not) = 0:32 and P(student = not) = 0:51. Then the ratio represents the conditional probability: 0.32/0.51 = 0.63.
27(a) This probability is \(\dfrac {P(parents = used and student = not)}{P(student = not)} = \dfrac {0.19}{0.51} = 0.37\). (b) The total equals 1. (c) Under the condition the student does not use drugs, the parents must either use drugs or not. The complement still appears to work when conditioning on the same information.
28No. This was an observational study. Two potential confounding variables include income and region. Can you think of others?
29Fenner F. 1988. Smallpox and Its Eradication (History of International Public Health, No. 6). Geneva: World Health rganization. ISBN 92-4-156110-6.
30P(result = died | inoculated = no) = \(\dfrac {P(result = died and inoculated = no)}{P(inoculated = no)} = \dfrac {0.1356}{0.9608} = 0.1411\).
| inoculated | |||
|---|---|---|---|
| yes | no | Total | |
| lived | 238 | 5136 | 5374 |
| died | 6 | 844 | 850 |
| Total | 244 | 5980 | 6224 |
| inoculated | |||
|---|---|---|---|
| yes | no | Total | |
| lived | 0.0382 | 0.8252 | 0.8634 |
| died | 0.0010 | 0.1356 | 0.1366 |
| Total | 0.0392 | 0.9608 | 1.0000 |
Exercise \(\PageIndex{1}\)
Determine the probability that an inoculated person died from smallpox. How does this result compare with the result of Exercise 2.44?
Solution
P(result = died | inoculated = yes) = \(\dfrac {P(result = died and inoculated = yes)}{P(inoculated = yes)} = \dfrac {0.0010}{0.0392} = 0.0255\). The death rate for individuals who were inoculated is only about 1 in 40 while the death rate is about 1 in 7 for those who were not inoculated.
Exercise \(\PageIndex{1}\)
The people of Boston self-selected whether or not to be inoculated. (a) Is this study observational or was this an experiment? (b) Can we infer any causal connection using these data? (c) What are some potential confounding variables that might influence whether someone lived or died and also a ect whether that person was inoculated?
Solution
Brief answers: (a) Observational. (b) No, we cannot infer causation from this observational study. (c) Accessibility to the latest and best medical care. There are other valid answers for part (c).
General Multiplication Rule
Section 2.1.6 introduced the Multiplication Rule for independent processes. Here we provide the General Multiplication Rule for events that might not be independent.
General Multiplication Rule
If A and B represent two outcomes or events, then
\[ P (A and B) = P (A | B) \times P (B)\]
It is useful to think of A as the outcome of interest and B as the condition.
This General Multiplication Rule is simply a rearrangement of the definition for conditional probability in Equation (2.40) on page 83.
Example \(\PageIndex{1}\)
Consider the smallpox data set. Suppose we are given only two pieces of information: 96.08% of residents were not inoculated, and 85.88% of the residents who were not inoculated ended up surviving. How could we compute the probability that a resident was not inoculated and lived?
Solution
We will compute our answer using the General Multiplication Rule and then verify it using Table 2.16. We want to determine
\[ P (result = lived and inoculated = no )\]
and we are given that
\[ P (\text{result = lived | inoculated = no}) = 0.8588 \]
\[ P (\text{inoculated = no}) = 0.9608\]
Among the 96.08% of people who were not inoculated, 85.88% survived:
\[ P (\text{result = lived and inoculated = no}) = 0.8588 X 0.9608 = 0.8251 \]
This is equivalent to the General Multiplication Rule. We can con rm this probability in Table 2.16 at the intersection of no and lived (with a small rounding error).
Exercise \(\PageIndex{1}\)
Use P(inoculated = yes) = 0:0392 and P(result = lived | inoculated = yes) = 0:9754 to determine the probability that a person was both inoculated and lived.33
33The answer is 0.0382, which can be veri ed using Table 2.16.
Exercise \(\PageIndex{1}\)
If 97.45% of the people who were inoculated lived, what proportion of inoculated people must have died?34
34There were only two possible outcomes: lived or died. This means that 100% - 97.45% = 2.55% of the people who were inoculated died.
Sum of conditional probabilities
Let A1, ..., Ak represent all the disjoint outcomes for a variable or process. Then if B is an event, possibly for another variable or process, we have:
\[ P ( A_1 | B ) + \dots + P ( A_k | B ) = 1\]
The rule for complements also holds when an event and its complement are conditioned on the same information:
\[ P ( A | B ) = 1 - P ( A^c | B ) \]
Exercise \(\PageIndex{1}\)
Based on the probabilities computed above, does it appear that inoculation is effective at reducing the risk of death from smallpox?35
35The samples are large relative to the difference in death rates for the "inoculated" and "not inoculated" groups, so it seems there is an association between inoculated and outcome. However, as noted in the solution to Exercise 2.46, this is an observational study and we cannot be sure if there is a causal connection. (Further research has shown that inoculation is effective at reducing death rates.)
Independence Considerations in Conditional Probability
If two processes are independent, then knowing the outcome of one should provide no information about the other. We can show this is mathematically true using conditional probabilities.
Exercise 2.51 Let X and Y represent the outcomes of rolling two dice. (a) What is the probability that the rst die, X, is 1? (b) What is the probability that both X and Y are 1? (c) Use the formula for conditional probability to compute P(Y = 1 | X = 1). (d) What is P(Y = 1)? Is this different from the answer from part (c)? Explain.36
We can show in Exercise 2.51(c) that the conditioning information has no influence by using the Multiplication Rule for independence processes:
\[ P ( Y = 1 | X = 1) = \dfrac {P (Y = 1 and X = 1 )}{P ( X = 1)}\]
\[ = \dfrac { P (Y = 1) X P ( X = 1)}{P (X = 1)}\]
\[ = P (Y = 1)\]
Exercise \(\PageIndex{1}\)
Ron is watching a roulette table in a casino and notices that the last ve outcomes were black. He figures that the chances of getting black six times in a row is very small (about 1=64) and puts his paycheck on red. What is wrong with his reasoning?37
Tree diagrams
Tree diagrams are a tool to organize outcomes and probabilities around the structure of the data. They are most useful when two or more processes occur in a sequence and each process is conditioned on its predecessors.
The smallpox data t this description. We see the population as split by inoculation: yes and no. Following this split, survival rates were observed for each group. This structure is reflected in the tree diagram shown in Figure 2.17. The first branch for inoculation is said to be the primary branch while the other branches are secondary.
Tree diagrams are annotated with marginal and conditional probabilities, as shown in Figure 2.17. This tree diagram splits the smallpox data by inoculation into the yes and no groups with respective marginal probabilities 0.0392 and 0.9608. The secondary branches are conditioned on the rst, so we assign conditional probabilities to these branches. For example, the top branch in Figure 2.17 is the probability that result = lived conditioned on the information that inoculated = yes. We may (and usually do) construct joint probabilities at the end of each branch in our tree by multiplying the numbers we come
36Brief solutions: (a) 1/6. (b) 1/36. (c) \(\dfrac {P(Y = 1 and X= 1)}{P(X= 1)} = \dfrac {1/36}{1/6} = 1/6\). (d) The probability is the same as in part (c): P(Y = 1) = 1/6. The probability that Y = 1 was unchanged by knowledge about X, which makes sense as X and Y are independent.
37He has forgotten that the next roulette spin is independent of the previous spins. Casinos do employ this practice; they post the last several outcomes of many betting games to trick unsuspecting gamblers into believing the odds are in their favor. This is called the gambler's fallacy.

across as we move from left to right. These joint probabilities are computed using the General Multiplication Rule:
\[ P ( inoculated = yes and result = lives ) \]
\[ = P (inoculated = yes ) X P(rest = | inoculated = yes )\]
\[ = 0.0392 X 0.9754 = 0.0382 \]
Example 2.53 Consider the midterm and nal for a statistics class. Suppose 13% of students earned an A on the midterm. Of those students who earned an A on the midterm, 47% received an A on the nal, and 11% of the students who earned lower than an A on the midterm received an A on the nal. You randomly pick up a final exam and notice the student received an A. What is the probability that this student earned an A on the midterm?
The end-goal is to nd P(midterm = A | final = A). To calculate this conditional probability, we need the following robabilities:
\[ P ( midterm = A and final = A ) and P (final = A) \]
However, this information is not provided, and it is not obvious how to calculate these probabilities. Since we aren't sure how to proceed, it is useful to organize the information into a tree diagram, as shown in Figure 2.18. When constructing a tree diagram, variables provided with marginal probabilities are often used to create the tree's primary branches; in this case, the marginal probabilities are provided for midterm grades. The nal grades, which correspond to the conditional probabilities provided, will be shown on the secondary branches.
With the tree diagram constructed, we may compute the required probabilities:
\[ P (midterm = A and final = A ) = 0.0611 \]
\[ P \underline {(final = A)} \]
\[ = P (midterm = other and \underline {final = A}) + P (midterm = A and \underline {final = A}) \]
\[ = 0.0611 + 0.0957 = 0.1568 \]
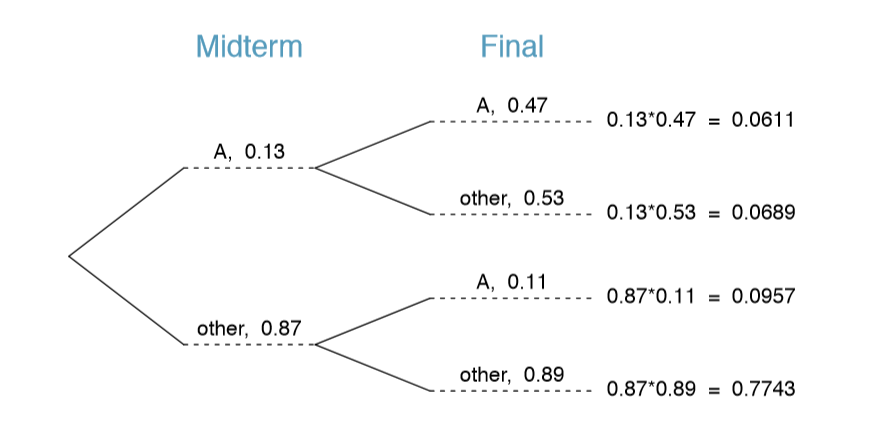
The marginal probability, P(final = A), was calculated by adding up all the joint probabilities on the right side of the tree that correspond to final = A. We may now nally take the ratio of the two probabilities:
\[ \text {P (midterm = A | final = A)} = \dfrac {P(midterm = A and final)}{P (final = A)}\]
\[ = \dfrac {0.0611}{0.1568} = 0.3897 \]
The probability the student also earned an A on the midterm is about 0.39.
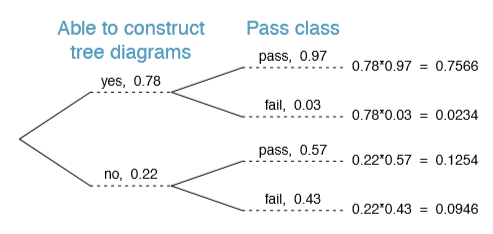
Exercise 2.54 After an introductory statistics course, 78% of students can successfully construct tree diagrams. Of those who can construct tree diagrams, 97% passed, while only 57% of those students who could not construct tree diagrams passed. (a) Organize this information into a tree diagram. (b) What is the probability that a randomly selected student passed? (c) Compute the probability a student is able to construct a tree diagram if it is known that she passed.38
Bayes' Theorem
In many instances, we are given a conditional probability of the form
\[ P(statement about variable 1 | statement about variable 2)\]
but we would really like to know the inverted conditional probability:
\[ P(statement about variable 2 | statement about variable 1)\]
Tree diagrams can be used to find the second conditional probability when given the first. However, sometimes it is not possible to draw the scenario in a tree diagram. In these cases, we can apply a very useful and general formula: Bayes' Theorem.
38(a) The tree diagram is shown below. (b) Identify which two joint probabilities represent students who passed, and add them: P(passed) = 0.7566 + 0.1254 = 0.8820. (c) P(construct tree diagram | passed) = \(\dfrac {0.7566}{0.8820} = 0.8578\).
We first take a critical look at an example of inverting conditional probabilities where we still apply a tree diagram.
Example \(\PageIndex{1}\)
n Canada, about 0.35% of women over 40 will be diagnosed with breast cancer in any given year. A common screening test for cancer is the mammogram, but this test is not perfect. In about 11% of patients with breast cancer, the test gives a false negative: it indicates a woman does not have breast cancer when she does have breast cancer. Similarly, the test gives a false positive in 7% of patients who do not have breast cancer: it indicates these patients have breast cancer when they actually do not.39 If we tested a random woman over 40 for breast cancer using a mammogram and the test came back positive { that is, the test suggested the patient has cancer { what is the probability that the patient actually has breast cancer?
Solution

39The probabilities reported here were obtained using studies reported at www.breastcancer.org and www.ncbi.nlm.nih.gov/pmc/articles/PMC1173421.
Notice that we are given sufficient information to quickly compute the probability of testing positive if a woman has breast cancer (1:00 - 0:11 = 0:89). However, we seek the inverted probability of cancer given a positive test result. Watch out for the non-intuitive medical language: a positive test result suggests the possible presence of cancer in a mammogram screening. This inverted probability may be broken into two pieces:
\[ P (has BC | mammogram^+) = \frac {P (has BC and mammogram^+)}{P (mammogram)}\]
where "has BC" is an abbreviation for the patient actually having breast cancer and \("mammogram^+"\) means the mammogram screening was positive. A tree diagram is useful for identifying each probability and is shown in Figure 2.19. The probability the patient has breast cancer and the mammogram is positive is
\[ { P(has BC and mammogram}^+\text{)} = P(mammogram^+ | has BC) P(has BC)\]
\[ = 0.89 \times 0.0035 = 0.00312 \]
The probability of a positive test result is the sum of the two corresponding scenarios:
\[ P (mammogram^+ ) = P (mammogram^+ and has BC) + P(mammogram^+and no BC)\]
\[ = P(has BC)P(mammogram^+ | has BC) + P(no BC)P(mammogram^+ | no BC)\]
\[= 0.00035 X 0.89 + 0.9965 \times 0.07 = 0.07288\]
Then if the mammogram screening is positive for a patient, the probability the patient has breast cancer is
\[P (has BC | mammogram^+) = \frac {P(has BC and mammogram^+)}{P(mammogram^+)}\]
\[= \frac {0.00312}{0.07288} \approx {0.0428}\]
That is, even if a patient has a positive mammogram screening, there is still only a 4% chance that she has breast cancer.


