2: Obtaining Useful Evidence
- Page ID
- 5320
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)A primary role of statistics is to use evidence from stochastic populations to improve our understanding of the world. Deciding what evidence will be collected is an essential part of the process. Research design is that portion of the statistical process in which planning is done so that the conclusions are drawn with confidence and can be supported under scrutiny.
There are three research designs we will explore in this chapter, observational studies, observational experiments, and manipulative experiments. The type of research that is conducted is dependent upon the objective of the research. In cases where the objective is to understand a population or compare populations, an observational studies is appropriate. In cases in which we want to determine if a causal relationship exists between two variables, we conduct an experiment. A causal relationship (cause and effect relationships) implies the existence of two variables. The variable that is the cause must happen first. The first variable is called an explanatory variable, the variable that is affected is a response variable.
In experiments, the explanatory variable is a treatment or intervention that is imposed upon people or elements of a population. Of the two experiments, observational and manipulative, the latter is better for showing a causal relationship. In manipulative experiments the researcher can randomly assign the treatment or intervention whereas for observational experiments, the treatment or intervention is imposed by someone other than the researcher.
Before clarifying each of these research designs, a few examples might be useful.
Examples of Observational Studies
- A researcher might conduct a survey of Americans to compare the proportion of Democrats who support efforts at reducing carbon emissions to the proportion of Republicans who want to reduce carbon emissions.
- Water samples could be taken in the Puget Sound to determine the level of PCB contamination.
- Students could be given an unannounced exam on a math skill they had learned earlier in the school year to see how much they retained.
Example of Observation experiments
- Since some states have legalized the recreational use of marijuana, it is possible to determine if it really a gateway drug by seeing if there is a change in the usage of harder drugs.
- When some states increase the minimum wage, it is possible to determine if raising the minimum wage has an effect on the number of people who are employed in the state by comparing them with states that don’t raise the minimum wage.
- When a natural disaster strikes an area, it is possible to determine the effect on donations to organizations such as the Red Cross.
Example of Manipulative experiments
- A coach randomly assigns some runners to a weight training program and does not allow other runners to lift weights, but otherwise all runners have the same training program, then the coach can determine the effect of weight training on running improvement.
- Loaves of homemade bread can be baked at different temperatures to determine the effect of temperature on the bread.
- A company can try different internet ads to see if there is an effect on sales of their product.
Randomness
Each research design incorporates one application of randomness. In the case of observational studies and observational experiments, a random selection is made from the population. This may be difficult for some observational experiments. For example, there are not enough states that have legalized marijuana to randomly select from. In manipulative experiments, the researcher randomly assigns participants to different groups, for example, to groups receiving a treatment and those not receiving it. The methods used for random selection and random assignment are discussed later in this chapter.
Distinguishing between research designs
It can be challenging to determine which research design is being used. The following questions can guide your decision.
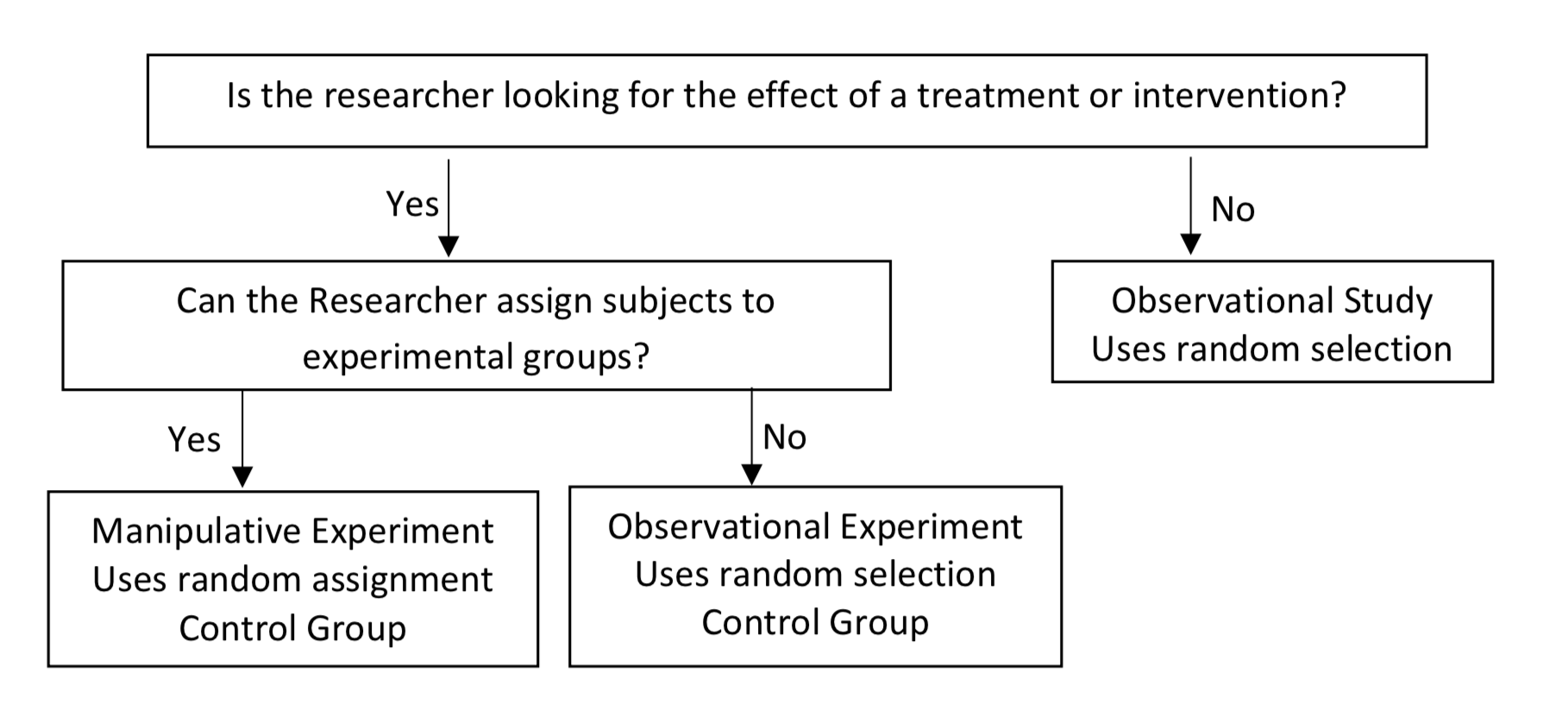
- Is the researcher looking for the effect of a treatment or intervention?
- If the answer to the first question is yes, then can the researcher randomly assign participants to different groups?
The flow chart that follows uses these questions to determine the type of research design.
Types-of-Research Flow Chart
Experiments
Policy makers, businesses managers, physicians, educators, scientists, and coaches typically have an outcome they would like to achieve, but they want to make an evidence-based decision in order to achieve the outcome. That is, they want to know what variable they can change so the change has an effect on a different variable. For example,
A policy maker may wonder what variable should be changed to reduce poverty.
A business manager may wonder what advertising strategy will lead to the greatest increase in sales.
A physician may wonder which medicine will cure a person.
An educator may wonder which teaching strategy will lead to the greatest amount of learning for the students.
For causal relationships, it has already been stated that a cause must proceed an effect, but there is another criterion of importance. In a causal relationship, a treatment produces a particular outcome while not providing the treatment means that particular outcome is not produced. Thus, simply showing that a certain response occurred when a treatment was provided does not prove the treatment caused the response. There could be another factor that caused that particular response. To prove causation, the research should be designed to show that one response occurs with the treatment and does not occur without the treatment and that there is unlikely to be another variable that is causing the response. This requires having at least two groups, one (or more) which receives the treatment and one that does not receive the treatment. The group that does not receive the treatment is called a control group.
When experiments are conducted on non-humans, it is possible to have a control group that does not receive any treatment. An example would be agriculture researchers who might fertilize some crops but not others. However, when an experiment is conducted on humans, there can be complications. In typical experiments involving the testing of new medicines on a person with an illness, it is not sufficient to simply give some people the medicine being tested and not give it to others. Humans can have psychosomatic effects – physical changes that are a result of the expectations of a certain effect of the medicine, attributed to the mind-body interactions. To address this problem, it is customary to give an inert medicine, called a placebo, to some of the participants. It is important that the subjects do not know if they are receiving the real medicine or the placebo. It is also important that the researcher examining the subjects doesn’t know either. This is achieved by doing a double blind experiment. In this type of experiment, subjects are randomly assigned to either the treatment group or the placebo group, but are not told which group they are in. The doctor is not told either.
A problem has been observed with this type of double blind experiment however. That problem is called breaking blind and is caused because subjects have to be warned about possible side effects from the medication. Consequently, those experiencing the side effects can guess they are taking the actual medicine and those that don’t experience them conclude they are taking the placebo. In some experiments, more than 80% of the doctors and subjects correctly identified if a subject was in the treatment group or placebo group. Since a correct guess about the group should occur about 50% of the time, it is likely that side effects, or possibly other clues, led to the higher value of correct identification. To help minimize this problem, some researchers use an active placebo instead of the more typical sugar pill. An active placebo produces side effects similar to the real medicine, but does not provide a cure for the medical condition.("Listening to Prozac, But Hearing Placebo." The Emperor's New Drugs: Exploding The Antidepressant Myth. Philadelphia: Basic Books, 2010. 7-20. Print.)
In medical studies, besides having a treatment group and a placebo group, it is appropriate to have a control group that receives no treatment at all. This is often accomplished because some people who apply to be in the experiment are not accepted. Because illnesses can go through cycles (good days, bad days) and people usually wait until they feel very bad to get treatment, then comparing the results of treatment to people who don’t receive any treatment can be helpful to show if something other than the normal cycle of symptoms is occurring as a result of the treatment.
Response variables, explanatory variables, levels, and confounding
Response and explanatory variables will be explained using teachers as an example. An ideal outcome for a teacher would be for the entire class of students to be successful in the class. The teacher would like to know which teaching strategies (pedagogy) will lead to the greatest success for the students. Notice in this example, there are two variables, teaching strategy and student success. Since teaching must come before assessment of student success, then teaching strategy is the explanatory variable and student success is the response variable.
The response variable is rather vague however. What does student success mean? There are many aspects of learning, such as memorization of facts, ability to calculate, skills in the laboratory, writing skills, ability to think critically, ability to think creatively, etc. A researcher needs to be clear about the response variable. For example, since this book is used for a statistics class, then one outcome of particular interest is whether students can correctly test a hypothesis. A different outcome might be whether the students can create appropriate graphs for the data.
There are many possibilities for the explanatory variable of teaching strategies. These possibilities are called levels. Examples of levels include lecturing, active learning, discovery learning, computer teaching software, etc. Levels are specific examples of the explanatory variable.
While teaching pedagogy is an explanatory variable a teacher can modify, it is not the only variable that can affect the response variable of student success. Other variables include student interest and motivation, the text, study time, distractions (lack of food or shelter, deployment of a spouse, divorce, illness, etc). These other variables, which could be used as explanatory variables in different research, are called confounding variables. Potential confounding variables should be identified during the research design stage so they can be controlled in the experiment by making sure that they are equally distributed in the different experimental groups.
To get practice identifying the different elements of research, you will be given stories that explain a research project. From the story, your object is to identify the key elements, including the research question, the variables, parameter, and type of research. These will be organized in a research design table. When completing this table, think of the potential confounding variables yourself as they are not usually included in the story.
| Research Design Table | |
| Research Question: | |
| Type of Research | Observational Study Observational Experiment Manipulative Experiment |
| What is the response variable? | |
| What is the parameter that will be calculated | Mean Proportion |
| List potential confounding variables. | |
| Grouping/Explanatory Variables 1 (if present) |
Levels: |
Some of the examples below contain underlined words, others do not. The purpose of underlining is to help you identify the key words in the story. Ultimately, you need to identify these parts without them being underlined.
Example 2.1 Is there a difference in the number of electronic items in the homes of people who were born and raised in the US compared to people who immigrated to the US and have lived in the US for at least 5 years?
To answer this question, the residency status of people will be classified as native or 5-year immigrant. A random samples of native residents and immigrants who have been in the US at least 5 years will be taken. All electronic items will be counted individually (e.g. cell phones, computers, TVs, radios). The objective is to determine if the mean number of electronic items is different for the two groups.
| Research Design Table | |
| Research Question: Is there a difference in the number of electronic items in the homes of people who were born and raised in the US compared to people who immigrated to the US and have lived in the US for at least 5 years? | |
| Type of Research | Observational Study Observational Experiment Manipulative Experiment |
| What is the response variable? | number of electronic items |
| What is the parameter that will be calculated? | Mean Proportion |
| List potential confounding variables. | Income, wealth, age, size of family |
| Grouping/explanatory Variables (if present) Residency status |
Levels: native 5-year immigrant |
Briefing 2.1 Bare Foot Running
In 2011, Vintage Books published the book “Born to Run: A hidden Tribe, Superathletes, and the Greatest Race the World Has Never Seen” by Christopher McDougall. One of the topics discussed was the concept of bare-foot running. The author argued that running bare foot (or with minimal protection between the sole of the foot and the ground) leads to a forefoot running style that leads to fewer injuries than those who run with padded shoes and use a heal strike.
A high school running coach would like to know if new runners using minimalist shoes that lead to a forefoot running style will have fewer injuries than new runners using padded shoes that lead to heal strikes. The coach uses a coin flip to randomly assign the type of shoe a new runner should wear. The coach will record this shoe choice and maintain an injury record for each athlete. Ultimately, the coach will determine if there is a difference in the proportion of runners from each group who are injured. Only new runners will be included because it would be difficult and perhaps inappropriate to change the running style of experienced runners.
| Research Design Table | |
| Research Question: Does running style make a difference in injuries? | |
| Type of Research | Observational Study bservational Experiment Manipulative Experiment |
| What is the response variable? | injury |
| What is the parameter that will be calculated? | Mean Proportion |
| List potential confounding variables. | Prior running experience, prior injuries, general fitness |
| Grouping/explanatory Variables (if present) Type of shoe |
Levels: minimalist shoes Padded shoes |
Example 2.3 Will raising the tax rate for the wealthy solve the national debt problem?
Every time a law is changed the country conducts an experiment. One would assume that lawmakers reflect carefully about the possible consequences of any change in law they approve. The country is now faced with a large national debt that has some lawmakers concerned and which occasionally attracts the interest of investors. There is also an ideological debate that persists about the benefits or consequences of raising taxes or cutting spending. A popular recommendation of some is to raise taxes on the wealthy.
Briefing 2.2 Marginal Tax Rate
Tax brackets are used to show the amount of tax paid for each dollar earned. The marginal tax rates for 2013 are shown in the table on the next page for people who are married filing jointly. (taxfoundation.org/article/us-...usted-brackets viewed 7/08/13)
A person earning $80,000 would pay 10% tax on the first $17,488, 15% tax on the money between $17,488 and $71,030, and 25% on the amount over $71,030.
The graph below shows the change in the marginal tax rate on the wealthiest Americans and the National Debt. From this graph we see that the national debt started rising a lot in the late 1970s and 1980s. We also notice this rise was preceded by big drops in the top marginal tax rates during the Reagan administration.
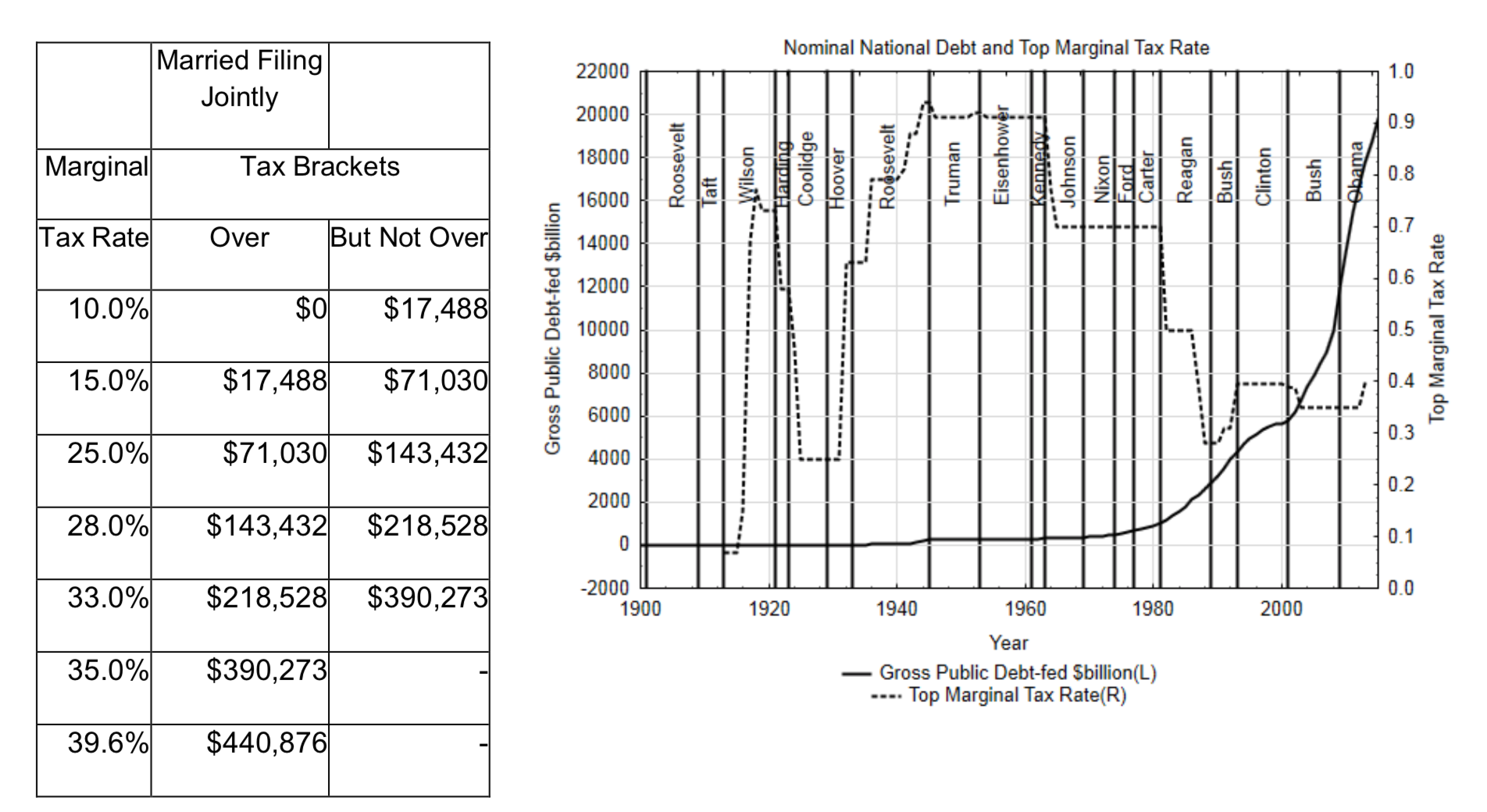
The information from this graph cannot be used to test the theory that lowering tax rates leads to increased national debt (or vice versa) because theories cannot be proved with the evidence that was used to create the theory in the first place. Therefore, if an economist wanted to test the theory about the effect of marginal tax rates on national debt, they will need to get different data. It would be unrealistic to expect that any country would agree to participate in an experiment in which a research economist would make them change their tax rates. However, countries do change tax rates on their own, so a researcher could observe what happens after each such change. The national debt before the rate change and 5 years after could be determined. If the goal is to establish a cause-and -effect relationship, it will also be necessary to identify changes in national debt for countries that do not change their tax rates. A comparison of the changes in national debt could be made for both groups. Other important aspects of national debt include the amount of spending that is done as well as the amount of concern legislators have with keeping the budget balanced.
| Research Design Table | |
| Research Question: Does lowering tax rates lead to an increase in national debt? | |
| Type of Research | Observational Study Observational Experiment Manipulative Experiment |
| What is the response variable? | Changes in national debt 5 years after rate change |
| What is the parameter that will be calculated? | Mean Proportion |
| List potential confounding variables. | State of the economy, number of people at each economic level, government budget priorities |
| Grouping/explanatory Variables (if present) Marginal tax rate change |
Levels: Control (did not change tax rates) Impact (reduced tax rates) |
Sampling
Observational studies and some observational experiments require random sampling from a population. The next step in the research design process is to determine how a sample will be taken from the population so that it is representative of the population. The objective is to avoid bias. Bias is systematic prejudice in one direction. Recall the sampling distributions that were discussed in Chapter 1. Half the statistics in the sampling distribution were less than the parameter and half were more, thus the probability of getting a statistic higher or lower than the parameter was the same. If sampling is not done correctly, it is easily possible to end up with biased results. That means that samples are more likely to be less than the parameter or they are more likely to be greater than the parameter. For example, if you want to determine which sport people think is the most exciting, pro football or pro soccer and you only sample people in a city with an NFL team, you are likely to get biased results in favor of pro football. On the other hand, if you conduct your survey in a city such as London, you are likely to get biased results in favor of soccer. Either way, you are getting biased results, which means any conclusion you draw is not valid.
Biased results are obtained when doing voluntary sampling and convenience sampling. Voluntary sampling occurs when people voluntarily agree to participate in a survey, such as an online survey or a TV survey where people can text their response. Convenience sampling occurs because of getting responses from people who are convenient. It is possible that these people share an opinion and consequently group together, resulting in biased results.
The best sampling is achieved using probability sampling methods. The four methods that will be discussed are:
- Simple Random Sampling
- Stratified Sampling
- Systematic Sampling
- Cluster Sampling
Simple Random Sampling
Simple random sampling meets two desirable criteria. First, every individual or unit in the population has an equal chance of being selected and second, every collection of selected units has an equal chance of being selected. The sampling distributions that underlie testing of hypotheses are based on simple random sampling with replacement. That means that once selected, a unit is put back into the pool and can be selected again. Consequently, information from the same unit can be used more than once.
The simplest example of a simple random sample is pulling names out of a hat. That is, everyone in a group can have their name written on a piece of paper and then put into a hat or other container. Someone mixes the pieces of paper and then pulls out a name. This is much like raffles that are done by organizations.
Putting names on a piece of paper quickly becomes unmanageable with larger populations and so a different strategy is needed. Instead, each person or unit is given a number and then numbers are selected. Data is then gathered from the person or unit with the selected number. Three different methods will be provided for doing a simple random sample. These methods make use of a table of random digits, the TI83 or TI84 calculator, and the website called Random.Org. The first two methods are known as pseudo-random meaning that while a random process is used to generate the numbers, it is a repeatable process. They will be explained below. The random numbers generated at Random.Org are truly random as they are based on atmospheric noise. Visit the website and select integer generator to try their selection process.
Table of Random Digits
A table of random digits consists of the digits 0 – 9 that have been randomly selected, with replacement. They are grouped with 5 digits together for visual convenience. Rows and columns are numbered.
To use the table, determine the size of the population from which a sample will be drawn. Assign a number to each person or unit in the population. The easiest way to do this is to assign a 1 to the first person (unit), a 2 to the second person (unit), etc. However, this is not the only strategy. People or units may already have a number (e.g. student ID number, production number), which can be used. The number of digits that will be selected at the same time corresponds to the number of digits in the largest assigned number. If the selection is to be done from a population of size 89 units, then since 89 is a 2-digit number, then assigned numbers will be 01, 02, ... 89 and all selections will be 2 digits. If the size of the population is 745, since this is a 3-digit number then the assigned numbers will be 001, 002, ... 745.
| Row | Col 1-5 | Col 6-10 | Col 11-15 | Col 16-20 | Col 21-25 | Col 26-30 | Col 31-35 | Col 36-40 |
|---|---|---|---|---|---|---|---|---|
| 1 | 05902 | 75968 | 00100 | 12330 | 92481 | 64625 | 83012 | 90763 |
| 2 | 53365 | 25560 | 86425 | 45946 | 67093 | 36638 | 71740 | 16878 |
| 3 | 69363 | 06820 | 49676 | 25363 | 96300 | 94376 | 65819 | 19636 |
| 4 | 37520 | 54955 | 31507 | 70745 | 41817 | 86606 | 97766 | 44989 |
| 5 | 10390 | 12738 | 54072 | 03238 | 08294 | 89479 | 03156 | 24217 |
| 6 | 98735 | 90798 | 96609 | 18368 | 74876 | 17403 | 33783 | 85101 |
| 7 | 79609 | 87687 | 77178 | 39784 | 76983 | 05689 | 84023 | 24804 |
| 8 | 00348 | 58777 | 90570 | 09114 | 99677 | 08126 | 76132 | 19334 |
| 9 | 98367 | 93351 | 08246 | 81492 | 57876 | 04366 | 21851 | 28620 |
| 10 | 34588 | 88493 | 61188 | 29234 | 32565 | 82010 | 07425 | 37173 |
| 11 | 74198 | 34943 | 64557 | 20118 | 25540 | 50014 | 29338 | 87231 |
| 12 | 00621 | 86824 | 81204 | 71923 | 03600 | 69080 | 31712 | 36599 |
| 13 | 44684 | 53902 | 86099 | 98640 | 86347 | 88061 | 60420 | 54118 |
| 14 | 43526 | 09310 | 21922 | 40743 | 64742 | 12780 | 88432 | 41496 |
| 15 | 37335 | 98934 | 61403 | 85336 | 76356 | 22349 | 31498 | 34136 |
| 16 | 25488 | 41567 | 32833 | 56973 | 04039 | 57733 | 88677 | 44817 |
| 17 | 45327 | 69347 | 85698 | 03248 | 60079 | 64469 | 71406 | 19478 |
| 18 | 47458 | 08093 | 94256 | 14305 | 42728 | 676159 | 35991 | 13527 |
| 19 | 91622 | 23621 | 91124 | 08233 | 54571 | 73527 | 29012 | 31534 |
| 20 | 77630 | 37356 | 85498 | 21296 | 14880 | 24981 | 70976 | 64922 |
For example, what will be the numbers of the first 3 people that would be selected from a population with 6890 people? People are assigned numbers such as 0001, 0002, ... 6890. The selection will begin in row 16, which is reproduced below. Four digits will be selected in a row. If they are less than or equal to 6890 they will be selected (shown with underlining). If they are larger than 6890, they will be ignored.
| 16 | 25488 | 41567 | 32833 | 56973 | 04039 | 57733 | 88677 | 44817 |
The first three numbers that are selected are 2548, 6732 and 0403.
The Texas Instrument TI84 calculator is able to generate random integers. A process that is analogous to picking a row in a table of random digits is to seed the calculator. The calculator is seeded and then random integers are selected. For example, if the seed number is 38, then the key strokes on the calculator would be:
38 sto math prb 1 rand enter. 38 should appear on the screen.
To generate the random number, the key strokes are:
math prb 5 randint, enter. The function randint expects the input of three numbers, the low, the high and the number of values you think will fit within the screen window. If we continue with the example of 6890 people, then since this is a 4 digit number we might expect 3 such numbers to fit on the screen, so we would enter: randint(1,6890,3). If we need more than 3 numbers, then we can just push enter again as often as is necessary.
The numbers that are selected in this example are: 2283, 3612, 3884.
Stratified Sampling
There are times when parts of the population might be expected to produce different data than other parts. For example, it might be expected that the concentration of a toxic chemical in the Puget Sound would be higher near industrial areas than in locations that are far from those industrial areas. Since random sampling may result in areas being missed, then a stratified sampling can be done. In this approach, areas are defined, with each area being a stratum. A simple random sampling process is then used within each stratum.
As a separate example, a group seeking to expand public transportation in a state may wonder how much support there would be for an initiative. They might expect the support for public transportation will be substantially different for people who use public transportation than for people who never use it. Consequently, they may do a simple random sampling from each of these groups.
It should be noticed that stratifying is based on the assumption that there will be differences between the strata although this may not be something that has been proved. This is different than actually having a hypothesis about the difference between the strata, in which case each stratum is considered to be a different population, rather than different parts of the same population.
Systematic Sampling
A sampling strategy this is particularly useful for sampling time series data is systematic sampling. This is a 1 in k sampling method in which every k\(^{\text{th}}\) unit is selected. Since the value of data in one year may be influenced by the previous year (or more), the data are not independent. For example, this year’s cost of tuition is closely related to last year’s cost. Suppose that a sample is to be taken from time series data that is serially dependent when the data are 1,2 and 3 years separated but not when they are separated by 4 years. In this case, sampling every 4t\(^{\text{th}}\) year would be appropriate. Suppose that data is available from 1961 to the present and a 1 in 4 systematic sampling method is used. What will be the first year in which data are selected? Since every year has to have a chance of being selected, then it will be necessary to randomize the initial value. This will be done by randomly selecting one number between one and k. To find successive numbers, add k to the number selected. For example, if a TI84 calculator is seeded with the number 42, then randint(1961,1964,1) will produce the number 1962. To this will be added 4 repeatedly until a sample of the desired size has been selected. The table below shows the years that will be selected.
| 1961 | 1962 | 1963 | 1964 | 1965 | 1966 | 1967 | 1968 | 1969 | 1970 |
| 1971 | 1972 | 1973 | 1974 | 1975 | 1976 | 1977 | 1978 | 1979 | 1980 |
The value of k is dependent upon the size of the population (N) and the size of the sample (n)and is found by dividing the former by the latter: \(K \thickapprox N/n\).
Cluster Sampling
Collecting data can be time consuming and expensive, neither of which is a trivial factor for any organization that needs the data. When data must be collected from different locations and there is not an assumption that the locations will cause the variation in the data, then cluster sampling can be used. For example, a community college may want to sample the student body about charging students a technology fee so that a new student computer lab can be built. Because students take many different classes and these classes are not likely to have a major impact on their preference about the fees, then different classes can be selected and all the students in those classes can be asked their preference on the fees. If a college has 450 classes, they can be numbered from 1 to 450 and a simple random sampling process can be used to select the desired number of classes. If the goal is to select 8 classes and a seed value of 16 is use, then on the TI84, the function Randint(1,450,4) will give the class numbers of 419, 313, 273, 229, 445, 162, 127, 428.
These methods are often confused. The following guidelines may help clarify the differences. Simple Random Sample – Random Sampling is done from the entire population.
Stratified Sampling – The entire population is divided into strata then simple random sampling is done from each strata. The samples from each strata are combined before being analyzed.
Systematic Sampling – One number is randomly selected from the first k numbers. The numbers of the other data are found by adding k to the last number that was selected.
Cluster Sampling – The entire population is divided into groups or clusters, which are given numbers. The groups are randomly selected and every unit within the group becomes part of the sample.
Chapter 2 Homework
Complete the design-layout tables. Use underlined words when available.
- A student would like to know which of two possible routes is faster for the daily trips to school. Route 1 is shorter but has many traffic lights. Route 2 is a little longer but doesn’t have traffic lights. Each morning, a coin flip will be used to determine the route taken to school. The time it takes for the commute will be measured with a stopwatch. After approximately 15 trials on each route, the average time for each will be compared.
Research Design Table Research Question: Type of Reserach Observational Study
Observational Experiment
Manipulative ExperimentWhat is the response variable? What is the parameter that will be calculated? Mean Proportion List potential confounding variables. Grouping/explanatory Variable (if present) Levels: - Suppose researchers wanted to know if the opinion people had about the future was influenced by the amount of news they consume (watched, listened to, or read). The researchers categorized news consumption into three categories: 5-7 days/week, 1-4 days/week, less than 1 day/week. They then asked the people their opinion of the future (if they expected the future to be better or worse than the present). They will compare the proportion of optimistic people in each group.
Research Design Table Research Question: Type of Reserach Observational Study
Observational Experiment
Manipulative ExperimentWhat is the response variable? What is the parameter that will be calculated? Mean Proportion List potential confounding variables. Grouping/explanatory Variable (if present) Levels: - Because so many species are becoming extinct, scientists would like to know how to increase biodiversity. There are two approaches to improve biodiversity in the world. The hands-off approach is one in which no one makes any deliberate changes to the environment with the intent of improving biodiversity. The deliberate approach is to deliberately introduce species that will reshape the environment, using surrogate species when necessary (e.g. use elephants instead of woolly mammoths, which are extinct). Examples of the first approach include the DMZ between North and South Korea. An example of the second includes the creation of a Pleistocene park in northeast Siberia by ecologist Sergei Zimov. Whether they occur by accident or design, there is no central planning organization that will randomly determine the approach that will be taken, so researchers can only look at the evidence after ecosystems have been engineered. A comparison will also be made with similar areas (control groups) that do not receive either the hands-off or deliberate approach. The researchers might record data on the increase in the number of species and determine if the average increase in number of species is different for the two approaches and the control groups. (Brand, Stewart. Whole Earth Discipline: An Ecopragmatist Manifesto. New York: Viking, 2009. Print.)
Research Design Table Research Question: Type of Reserach Observational Study
Observational Experiment
Manipulative ExperimentWhat is the response variable? What is the parameter that will be calculated? Mean Proportion List potential confounding variables. Grouping/explanatory Variable (if present) Levels:  a. It has been hypothesized that a lack of flexibility of the hamstring muscles can contribute to poor posture. To determine if that is the case, a group of adults was randomly selected. The group was divided into two, those with good posture and those with poor posture. The flexibility of their hamstrings was measured using a sit and reach test.(http://silbergen564s15.weebly.com/. Viewed 4/8/2017) The further a person can reach, the greater their hamstring flexibility.
a. It has been hypothesized that a lack of flexibility of the hamstring muscles can contribute to poor posture. To determine if that is the case, a group of adults was randomly selected. The group was divided into two, those with good posture and those with poor posture. The flexibility of their hamstrings was measured using a sit and reach test.(http://silbergen564s15.weebly.com/. Viewed 4/8/2017) The further a person can reach, the greater their hamstring flexibility.
Research Design Table Research Question: Type of Reserach Observational Study
Observational Experiment
Manipulative ExperimentWhat is the response variable? What is the parameter that will be calculated? Mean Proportion List potential confounding variables. Grouping/explanatory Variable (if present) Levels: b. Two types of stretching can be done to improve flexibility, static stretching and dynamic stretching. Static stretching involves stretching a muscle and holding it in a stretched position for about 30 sec. Dynamic stretching involves stretching while moving through a range of motion. To determine which type of stretching resulted in improvement, the group of people with poor hamstring flexibility were randomly assigned to one of three groups. One group did static stretching daily for one month. Once group did dynamic stretching daily for one month. The third group was the control group, which did not do any stretching. Afterwards, the subjects were retested and categorized as improving or not improving since their first test.
Research Design Table Research Question: Type of Reserach Observational Study
Observational Experiment
Manipulative ExperimentWhat is the response variable? What is the parameter that will be calculated? Mean Proportion List potential confounding variables. Grouping/explanatory Variable (if present) Levels: - Researchers want to know the proportion of acres of forest in the state that show evidence of the brown beetle infestation.
Research Design Table Research Question: Type of Reserach Observational Study
Observational Experiment
Manipulative ExperimentWhat is the response variable? What is the parameter that will be calculated? Mean Proportion List potential confounding variables. Grouping/explanatory Variable (if present) Levels: - A teacher wants to know the mean amount of time community college students spend doing homework each night.
Research Design Table Research Question: Type of Reserach Observational Study
Observational Experiment
Manipulative ExperimentWhat is the response variable? What is the parameter that will be calculated? Mean Proportion List potential confounding variables. Grouping/explanatory Variable (if present) Levels: - A fisheries biologist want to know the average weight of Coho Salmon returning to spawn.
Research Design Table Research Question: Type of Reserach Observational Study
Observational Experiment
Manipulative ExperimentWhat is the response variable? What is the parameter that will be calculated? Mean Proportion List potential confounding variables. Grouping/explanatory Variable (if present) Levels: - In Chapter 2, you were introduced to sampling distributions. Understanding these distributions proves challenging for many but since they form the bases upon which p-values are determined and therefore conclusions are drawn, knowing how the distributions are created and what they mean is helpful for your understanding of statistics. Sampling distributions are really theoretical in nature because they would be extremely difficult to make in reality, but having the experience of partially making one should give you greater insight into what one would really be like. In this problem, you are given a set of data, which is considered the entire population. Each data value has been numbered. You will then practice the various sampling methods multiple times, using different seed values. In each case, you will determine the statistic of the sample, which in this case will be a sample proportion. You will then fill in one box in the distribution that is provided. The first box you put in should be considered the one and only sample that you would have taken. Use a different color for shading the box. The remaining samples you take will represent other possible samples that you would have gotten with a different seed number.
The population consists of all the berths in a harbor. Each dock has room for 20 boats. In this problem, each cluster is a different dock. The two strata are the west side of the harbor and the east side. Yes means there is a boat at the berth, no means that it is vacant.
West Side of Harbor East Side of Harbor Cluster 1 Cluster 2 Cluster 3 Cluster 4 Cluster 5 Cluster 6 Cluster 7 1 Yes 21 No 41 Yes 61 No 81 101 121 2 Yes 22 No 42 No 62 No 82 Yes 102 122 Yes 3 No 23 No 43 No 63 No 83 103 Yes 123 4 Yes 24 No 44 Yes 64 No 84 104 Yes 124 5 No 25 No 45 No 65 No 85 Yes 105 Yes 125 Yes 6 Yes 26 Yes 46 Yes 66 No 86 Yes 106 No 126 No 7 No 27 No 47 No 67 Yes 87 No 107 No 127 Yes 8 Yes 28 No 48 No 68 No 88 No 108 Yes 128 No 9 No 29 No 49 No 69 No 89 Yes 109 No 129 Yes 10 No 30 No 50 No 70 Yes 90 No 110 No 130 No 11 No 31 No 51 Yes 71 No 91 No 111 No 131 No 12 Yes 32 No 52 Yes 72 Yes 92 Yes 112 Yes 132 Yes 13 Yes 33 No 53 Yes 73 Yes 93 No 113 No 133 No 14 Yes 34 No 54 Yes 74 Yes 94 Yes 114 No 134 Yes 15 35 Yes 55 No 75 Yes 95 No 115 No 135 No 16 36 Yes 56 No 76 Yes 96 No 116 No 136 No 17 Yes 37 Yes 57 No 77 No 97 Yes 117 Yes 137 Yes 18 Yes 38 Yes 58 No 78 Yes 98 No 118 Yes 138 No 19 No 39 No 59 Yes 79 No 99 No 119 Yes 139 Yes 20 No 40 No 60 No 80 No 100 No 120 Yes 140 Yes For each sampling method, 20 samples will be taken. Sample with replacement, which means the same number can be selected more than once. Determine the proportion of samples that are Yes. On each line, write the number selected and a Y for yes or N for no (e.g. 8Y)
- In Chapter 2, you were introduced to sampling distributions. Understanding these distributions proves challenging for many but since they form the bases upon which p-values are determined and therefore conclusions are drawn, knowing how the distributions are created and what they mean is helpful for your understanding of statistics. Sampling distributions are really theoretical in nature because they would be extremely difficult to make in reality, but having the experience of partially making one should give you greater insight into what one would really be like. In this problem, you are given a set of data, which is considered the entire population. Each data value has been numbered. You will then practice the various sampling methods multiple times, using different seed values. In each case, you will determine the statistic of the sample, which in this case will be a sample proportion. You will then fill in one box in the distribution that is provided. The first box you put in should be considered the one and only sample that you would have taken. Use a different color for shading the box. The remaining samples you take will represent other possible samples that you would have gotten with a different seed number.
- a. Use a simple random sample. The seed number for what will be considered the official sample is 5.
_______, _______, _______, _______, _______, _______, _______, _______, _______, _______,
_______, _______, _______, _______, _______, _______, _______, _______, _______, _______,Sample Proportion ______
The following are alternate sample results you could get if you had used different sampling methods and seed numbers.
b. Use a stratified sample with a seed number of 10 for the West and 11 for the East.
West ______, ______, ______, ______, ______,______, ______, ______, ______, ______,______,
East _______, _______, _______, _______, _______,_______, _______, _______, _______
Sample Proportion ______c. Use systematic sampling with a seed number of 15. Let k = 7.
_______, _______, _______, _______, _______, _______, _______, _______, _______, _______,
_______, _______, _______, _______, _______, _______, _______, _______, _______, _______,Sample Proportion ______
d. Use a cluster sampling method with a seed number of 20.
Which cluster is selected? ___________ Sample Proportion _________8e. Use a simple random sample with a seed number of 25._______, _______, _______, _______, _______, _______, _______, _______, _______, _______,
_______, _______, _______, _______, _______, _______, _______, _______, _______, _______,Sample Proportion ______
f. Use a stratified sample with a seed number of 30 for the West and 31 for the East.
West ______, ______, ______, ______, ______,______, ______, ______, ______, ______,______,
East _______, _______, _______, _______, _______,_______, _______, _______, _______Sample Proportion ______
g. Use systematic sampling with a seed number of 35. Let k = 7.
_______, _______, _______, _______, _______, _______, _______, _______, _______, _______,
_______, _______, _______, _______, _______, _______, _______, _______, _______, _______,Sample Proportion ______
h. Use a cluster sampling method with a seed number of 40.
Which cluster is selected? ___________ Sample Proportion _________
i. Use a simple random sample with a seed number of 45._______, _______, _______, _______, _______, _______, _______, _______, _______, _______,
_______, _______, _______, _______, _______, _______, _______, _______, _______, _______,Sample Proportion ______
j. Use a stratified sample with a seed number of 50 for the West and 51 for the East.
West ______, ______, ______, ______, ______,______, ______, ______, ______, ______,______,
East _______, _______, _______, _______, _______,_______, _______, _______, _______
Sample Proportion ______k. Use a cluster sampling method with a seed number of 55. Which cluster is selected? ___________ Sample Proportion _________
l. Use systematic sampling with a seed number of 60. Let k = 7.
_______, _______, _______, _______, _______, _______, _______, _______, _______, _______,
_______, _______, _______, _______, _______, _______, _______, _______, _______, _______,Sample Proportion ______
m. Fill in a square in the appropriate column, starting at the bottom row (that does not contain the numbers). The first sample proportion you get (from problem 8a) should be shaded differently than the rest of the sample proportions.0.00 0.05 0.10 0.15 0.20 0.25 0.30 0.35 0.40 0.45 0.50 0.55 0.60 0.65 0.70 0.75 0.80 0.85 0.90 0.95 1.00
n. Find the parameter by finding the proportion of all the 140 responses that are yes. Show this on the chart in 8m. How do the sample proportions compare to the population proportion? - The first graph shows the change in employment when the Federal minimum wage has been increased. This graph shows a comparison in the number of people employed 6 months after the increase, compared to six months before the increase. The numbers on the x-axis represent millions of people (e.g. 1000 x 1000) with positive numbers reflecting an increase in employment. Notice that most of the time, minimum wage went up, so did employment. However, this graph does not provide solid evidence that raising the minimum wage leads to an increase in employment. This is because there is no comparison. It could be that jobs were increasing or decreasing anyway, because of bigger economic changes, and that the minimum wage had only minor effect.
A better way to determine the effect of raising the minimum wage is to compare states that raise it with states that don’t since states have the ability to raise the minimum wage above the Federal level. The average after – before change in annual unemployment can be compared between these groups of states. For example, if the minimum wage in a state is increased in 2003, then the unemployment rate in 2002 can be subtracted from the unemployment rate in 2003. If the 2003 rate is lower than the 2002 rate, it means the unemployment rate went down and the difference would be a negative number. (Note: while the graph above was about the number of employed people, the graphs that follow are about the number of unemployed people).
a. Complete the Research Design table.Research Design Table Research Question: Type of Reserach Observational Study
Observational Experiment
Manipulative ExperimentWhat is the response variable? What is the parameter that will be calculated? Mean Proportion List potential confounding variables. Grouping/explanatory Variable (if present) Levels: Hypotheses and the level of significance are to be established before data is collected. The hypotheses for this question are that the average after-before difference in annual unemployment rates is different in the states that raise their minimum wage compared to states that don’t.
\(H_0: \mu_{\text{Raise}} = \mu_{\text{Not Raise}}\)
\(H_1: \mu_{\text{Raise}} \ne \mu_{\text{Not Raise}}\)
\(\alpha = 0.05\)From the table at http://www.dol.gov/whd/state/stateMinWageHis.htm, minimum wage data is available for consecutive years from 2000 to 2013, with an indication of rate changes beginning in the year 2001. Sampling from this set of data will be done by selecting 3 different years and using all the data from those years.
b. What is the name of the sampling method that is being used? ________________________
Which three years will be selected if your TI84 calculator is seeded with the number 42 and the years 2001 thru 2012 can be selected? These years were chosen because there is minimum wage increase data for these years and unemployment records for the year of, and the year before the unemployment rate increased, are available. Unemployment rates are found at http://www.bls.gov/lau/tables.htm.
c. Which years are selected? _______, ________, _________
The two graphs below are of the actual After-Minus-Before change in unemployment rates for the various states in the years that were randomly selected.
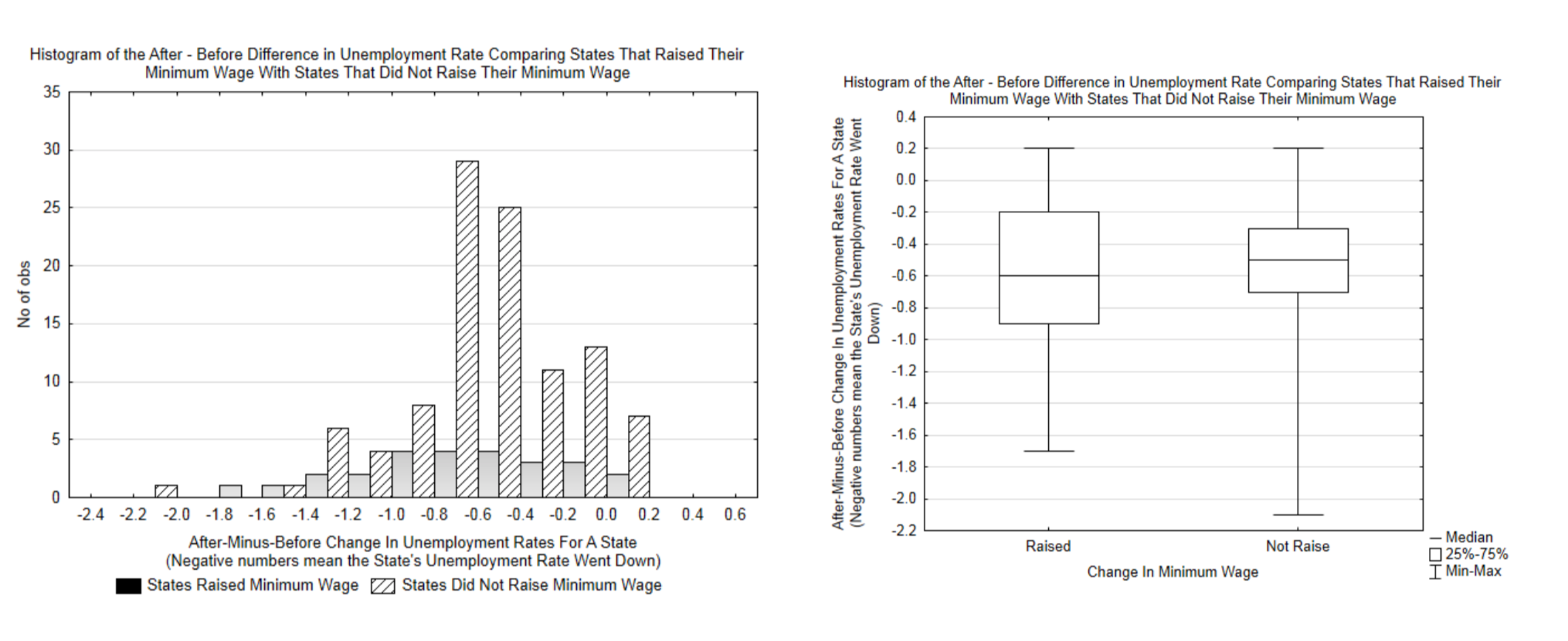
d. Do the graphs appear to support the null hypothesis or the alternate hypothesis better?
e. Both graphs are based on the same data. Which graph do you think shows the data better? Why?
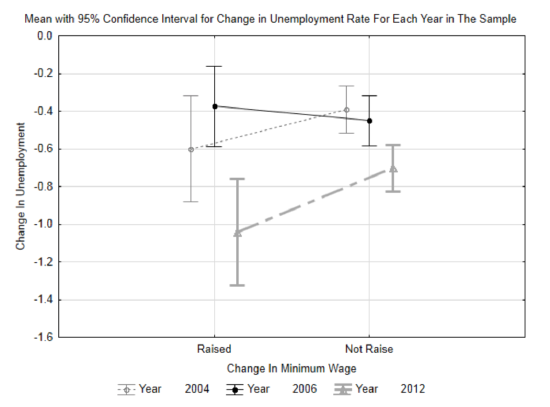 One additional graph is shown to the right. It includes concepts that will be discussed near the end of the book, but because this topic is of interest to the many people working at minimum wage, the graph is being included here. Each line is for a different year. The mean for each year is in the center of the vertical bar. The vertical bars on the left show the change in unemployment for the states that raised their minimum wage and the vertical bars on the right are for the states that did not. The bars represent the confidence interval. Since decreasing unemployment is viewed as desirable, then this graph shows that in two of the years (2004 and 2012), the states that raised their minimum wage reduced their unemployment rate more than the states that didn’t raise their rates. In 2006, the states that didn’t raise their minimum wage reduced their unemployment rate more than the states that did raise their rates.
One additional graph is shown to the right. It includes concepts that will be discussed near the end of the book, but because this topic is of interest to the many people working at minimum wage, the graph is being included here. Each line is for a different year. The mean for each year is in the center of the vertical bar. The vertical bars on the left show the change in unemployment for the states that raised their minimum wage and the vertical bars on the right are for the states that did not. The bars represent the confidence interval. Since decreasing unemployment is viewed as desirable, then this graph shows that in two of the years (2004 and 2012), the states that raised their minimum wage reduced their unemployment rate more than the states that didn’t raise their rates. In 2006, the states that didn’t raise their minimum wage reduced their unemployment rate more than the states that did raise their rates.
f. The table below shows the average change in unemployment rates for all the data combined. Which hypothesis do these statistics support?States Raised Minimum Wage States Did Not Raise Minimum Wage Mean -0.615 -0.519 n 26 105 g. The p-value for a comparison of the two means is 0.286. Write a concluding sentence in the style used in scholarly journals (like you were taught in Chapter 1).
h. Suppose you were in a class in which this topic was being discussed. What would you say to a classmate who argued that the minimum wage should not be raised because it will lead to more unemployment?
What would you say to the classmate who argued that the minimum wage should be raised because it means the poorer people will have more money to spend which means businesses will do better and have to hire more people thereby causing unemployment to drop even more?
- Why Statistical Reasoning Is Important for a Nursing Student and Professional Developed in collaboration with Becky Piper, Pierce College Puyallup Nursing Program Director This topic is discussed in NURS 112.
This problem is based on An Analysis of Falls in the Hospital: Can We Do Without Bedrails?by H.C. Hanger, M.C. Ball and L.A. Wood. the American Geriatrics Society, 47:529-531.
There was a time when women who helped the sick and injured were poorly regarded. However, in 1844, Florence Nightingale, daughter of a British banker, started visiting hospitals and learning about the care of patients. She eventually provided leadership to the British field hospitals during the Crimean War of 1853-56.(http://en.Wikipedia.org/wiki/Crimean_War) While her efforts helped improve the quality of the hospitals, it was after the war that she reflected about results she considered disappointing. She sought the assistance of William Farr who had recently invented the field of medical statistics. To help Florence understand the reasons for all the deaths in the hospital, he suggest that “We do not want impressions, we want facts.” One of her theories had been that many of the deaths were the result of inadequate food and supplies. The statistics lead to a rejection of this theory and instead pointed to lack of sanitation as a cause.(https://www.sciencenews.org/article/...e-statistician) Nightingale was also known for her use of graphs as a way of showing her analysis. Because of Florence Nightingale, the profession of Nursing is inextricably linked with statistics. In the modern context, it is called “evidence-based practices”.
Because hospital patients, particularly the elderly, have physical and possible cognitive problems that required placement in a hospital or nursing home, there is a need for nurses to keep the patients safe. One problem for these patients is falls, including falling out of bed. A standard practice for facilities has been to use bedrails so that a patient doesn’t accidently roll out of bed.
The researchers who wrote the article could find no evidence that bedrails prevented falls, so they conducted their own experiment. They instituted a policy at their hospital (in Christchurch, NZ) to discontinue the use of bedrails unless there was a justifiable reason for their use that was documented and approved. Their experiment was to compare the average number of falls per 10,000 bed days after the implementation of the policy to before its implementation. If the bedrails helped reduce falls, the number of falls should increase after they are removed.
\(H_0: \mu_{\text{after}} = \mu_{\text{before}}\)
\(H_1: \mu_{\text{after}} > \mu_{\text{before}}\)
\(\alpha = 0.05\)
a. Complete the experiment design tableResearch Design Table Research Question: Type of Reserach Observational Study
Observational Experiment
Manipulative ExperimentWhat is the response variable? What is the parameter that will be calculated? Mean Proportion List potential confounding variables. Grouping/explanatory Variable (if present) Levels: b. Before implementing the policy, the average number of falls per 10,000 bed days was 164.8 (S.D. = 20.6). After the new policy was implemented, the average number of falls per 10,000 bed days was 191.7 (S.D. = 40.7). The p-value was 0.18. Write a complete concluding sentence.
c. An additional part of the experiment was to compare the severity of the falls. Falls were classified as serious injury, minor injury or no injury. The table below shows the distribution of the injuries.Pre-policy Post-policy Serious injury 33 18 Minor injury 43 60 No injury 110 154 There is a significant difference in the injuries (p = 0.008). Explain what the difference is and give a possible reason for the difference.
d. If you were a nurse, would you suggest that bedrails be required or be removed? Why?


