3.4: Linear Functions
- Page ID
- 34411
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)A Linear Function is a function that has the form \(f(x) = mx+b\). Any line that can be expressed in the form \(y = mx + b\) is also a function.
Use function notation when an equation of a line written in Slope-Intercept form has no gaps or breaks and the line is not a vertical line. Linear functions written as \(f(x) = mx + b\) pass the vertical line test:
The Vertical Line Test is used to determine whether a graph defines the vertical output as a function of the horizontal input. If any vertical line would cross the graph more than once, then the graph does not define only one vertical output for each horizontal input.
For more information about linear equations, refer to the section on Straight Lines.
Create a table of solutions and graph the following linear functions:
\(f(x) = 2x − 3\)
Solution
\(f(x) = 2x − 3\)
To find two ordered pairs, choose small values of \(x\), then compute values of \(f(x)\).
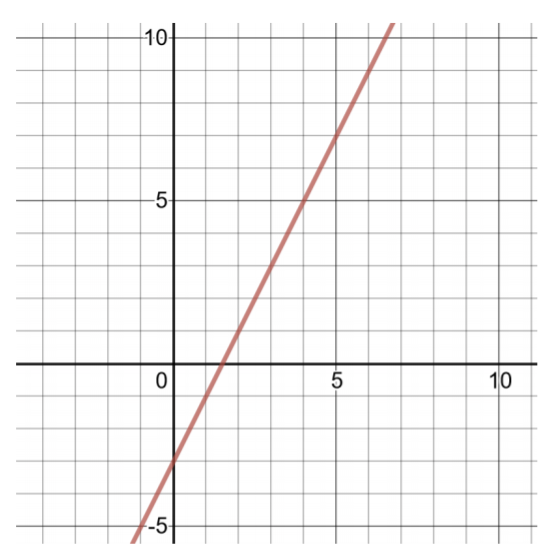Figure 4.4.1
| Table of Solutions for \(f(x) = 2x − 3\) | |
| \(x\) | \(f(x)\) |
| -1 | \(f(−1) = 2(−1) − 3 = −2 − 3 = −5\) |
| 0 | \(f(0) = 2(0) − 3 = 0 − 3 = 3\) |
Create a table of solutions and graph the following linear function:
\(g(x) = \dfrac{1}{ 3} x + 4\)
Solution
To find two ordered pairs, choose small values of x, then compute values of \(g(x)\). Because the coefficient of the term containing x is a fraction, choose multiples of the denominator for the product of \(\dfrac{1 }{3} x\) to be an integer.
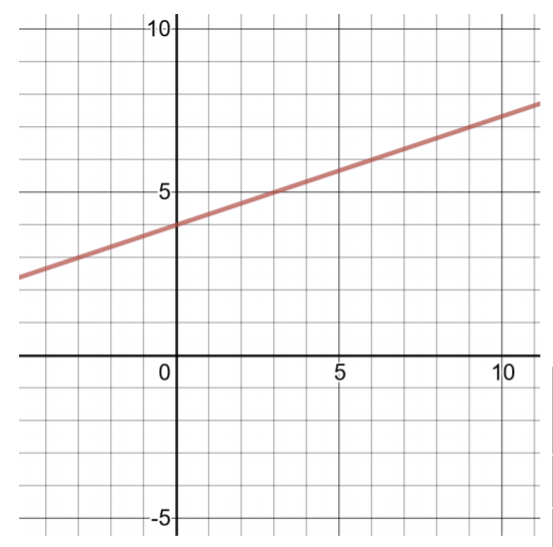Figure 4.4.2
| Table of Solutions for \(g(x) =\dfrac{ 1 }{3} x + 4\) | |
| \(x\) | \(g(x)\) |
| 0 | \(g(0) = \dfrac{1 }{3} (0) + 4 = 4\) |
| 3 | \(g(3) = \dfrac{1 }{3} (3) + 4 = 1 + 4 = 5\) |
Create a table of solutions and graph the following linear functions:
\(h(x) = −4x − 1\)
Solution
To find two ordered pairs, choose small values of \(x\), then compute values of \(h(x)\).
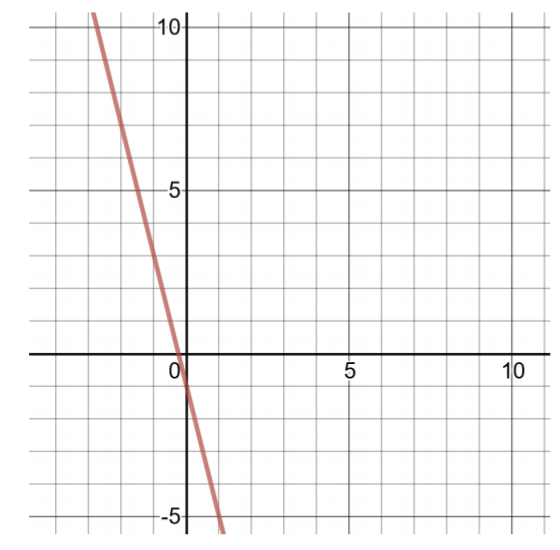Figure 4.4.3
| Table of Solutions for \(h(x) = −4x − 1\) | |
| \(x\) | \(h(x)\) |
| 0 | \(h(0) = −4(0) − 1 = −1\) |
| 1 | \(h(1) = −4(1) − 1 = −5\) |
Create a table of solutions and graph the following linear functions:
\(h(x) = − \dfrac{3 }{4} x − \dfrac{1 }{4}\)
Solution
To find two ordered pairs, choose small values of \(x\), then compute values of \(h(x)\).Because the coefficient of the term containing \(x\) is a fraction, choose multiples of the denominator for the product of \(− \dfrac{3}{4} x\) to be an integer.
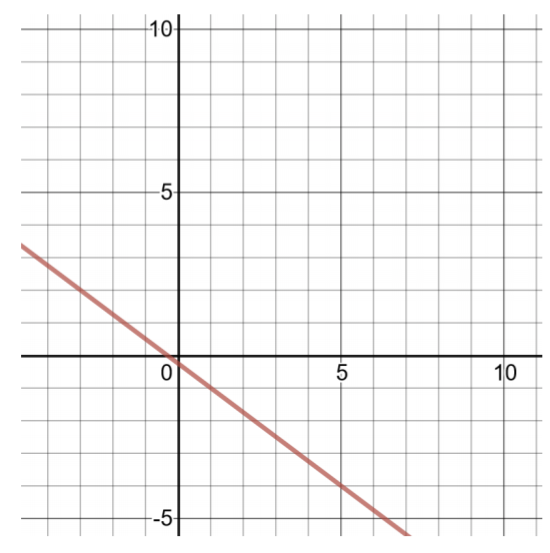Figure 4.4.4
| Table of Solutions for \(h(x) = − \dfrac{3}{4} x − \dfrac{1}{4}\) | |
| \(x\) | \(h(x)\) |
| 0 | \(h(0) = − \dfrac{3}{4} (0) − \dfrac{1}{4} = − \dfrac{1}{4}\) |
| 4 | \(h(4) = − \dfrac{3}{4} (4) − \dfrac{1}{4} = −3 − \dfrac{1}{4} = −3 \dfrac{1}{4}\) |
Create a table of solutions and graph the following linear functions:
- \(f(x) = 4x − 9\)
- \(g(x) = \dfrac{1}{ 2} x − 2\)
- \(h(x) = −3x + 5\)
- \(f(x) = − \dfrac{2}{ 3} x −\dfrac{ 1 }{3}\)