7.2: The Area of a Rectangle and Square
- Page ID
- 24854
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)The measurement of the area of geometric figures is one of the most familitax ways mathematics is used in our daily lives. The floor space of a building, the stae of a picture, the amount of paper in a roll of paper towels are all examples of Items often measured in terms of area. In this chapter we will derive formulas for the areas of the geometric objects which we have studied.
Area is measured in square inches, square feet, square centimeters, etc. The bastc unit of measurement is the unit square, the square whose sides are of length 1 (Figure \(\PageIndex{1}\)). Its area Is 1 square inch, 1 square foot, 1 square centimeter, etc., depending on which measurement of Iength is chosen. The area of any closed figure is defined to be the number of unit squares it contains.
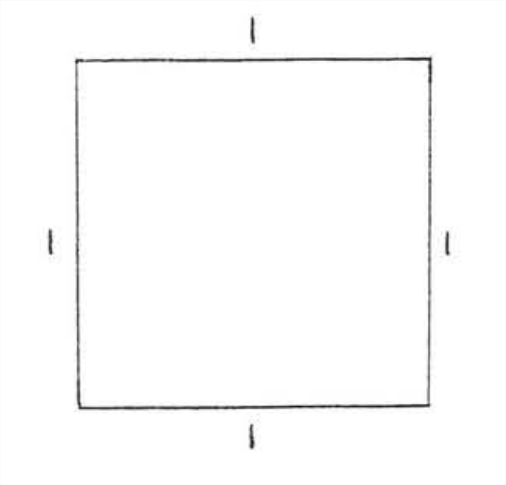 Figure \(\PageIndex{1}\): The unit square.
Figure \(\PageIndex{1}\): The unit square.
Find the area of a rectangle with length 5 and width 3.
Solution
We see from the diagram that the area is \((5)(3)=15\)
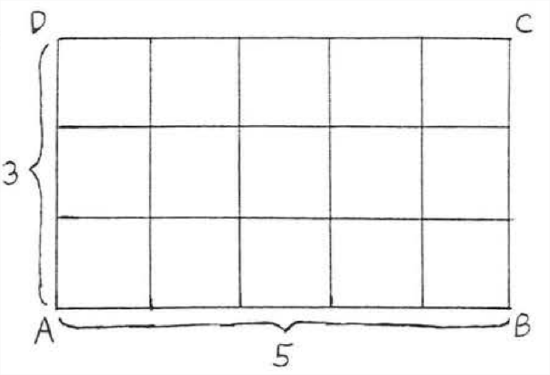
Answer: 15.
This suggests the following theorem:
The area of a rectangle is the length times its width.
\(A = lw\)
Find the area of a square with side 3.
Solution
Area = \((3)(3) = 3^2 = 9\).
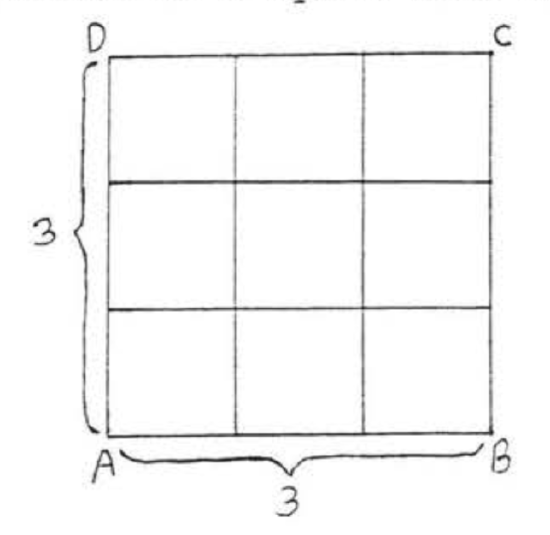
Answer: 9.
The formula for a squa:re is now self-evident:
The area of a square is the square of one of its sides.
\(A = s^2\)
The perimeter of a polygon is the su.m of the lengths of its sides. For instance the perimeter of the rectangle of Example \(\PageIndex{1}\) would be 5 + 5 + 3 + 3 = 16.
Find the area and perimeter of rectangle \(ABCD\):
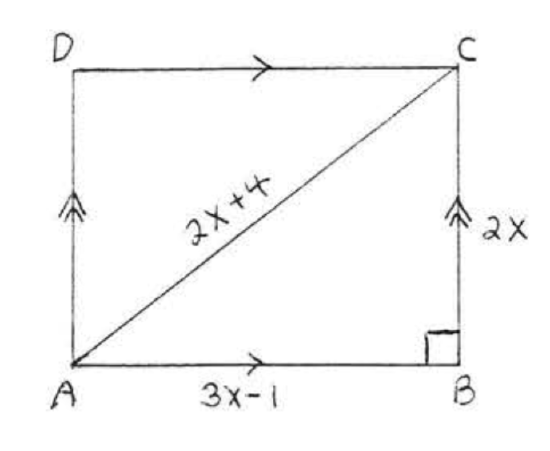
Solution
We first use the Pythagorean Theorem to find \(x\):
\(\begin{array} {rcl} {AB^2 + BC^2} & = & {AC^2} \\ {(3x - 1)^2 + (2x)^2} & = & {(2x + 4)^2} \\ {9x^2 - 6 x + 1 + 4x^2} & = & {4x^2 + 16x + 16} \\ {9x^2 - 22x - 15} & = & {0} \\ {(9x + 5)(x - 3)} & = & {0} \end{array}\)
\(\begin{array} {rcl} {9x + 5} & = & {0} \\ {x} & = & {-\dfrac{5}{9}} \end{array}\) \(\begin{array} {rcl} {x - 3} & = & {0} \\ {x} & = & {3} \end{array}\)
We reject the answer \(x = -\dfrac{5}{9}\) because \(BC = 2x = 2(-\dfrac{5}{9}) = -\dfrac{10}{9}\) would have negative length. Therefore \(x = 3\).
\(AB = 3x - 1 = 3(3) - 1 = 9 - 1 = 8\). \(BC = 2x = 2(3) = 6\).
\(AC = 2x + 4 = 2(3) + 4 = 6 + 4 = 10\).
Check:

Area = \(lw = (8)(6) = 48.\) Perimeter = 8 + 8 + 6 + 6 = 28.
Answer: Area = 48, Perimeter = 28.
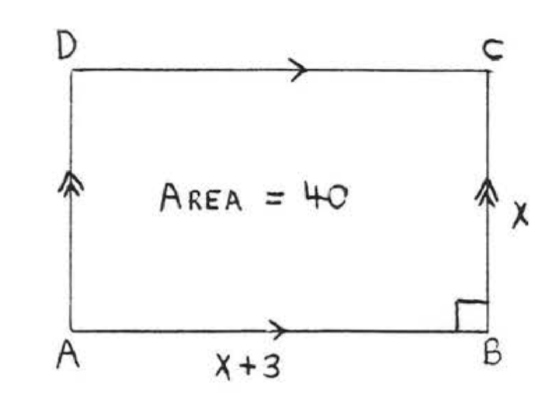
Find \(x\):
Solution
\(\begin{array} {rcl} {A} & = & {lw} \\ {40} & = & {(x + 3)(x)} \\ {40} & = & {x^2 + 3x} \\ {0} & = & {x^2 + 3x - 40} \\ {0} & = & {(x - 5)(x + 8)} \\ {x} & = & {5\ \ \ \ \ \ \ x = -8} \end{array}\)
We reject \(x = -8\) because side \(BC = x\) of the rectangle would be negative.
Check, \(x = 5\):
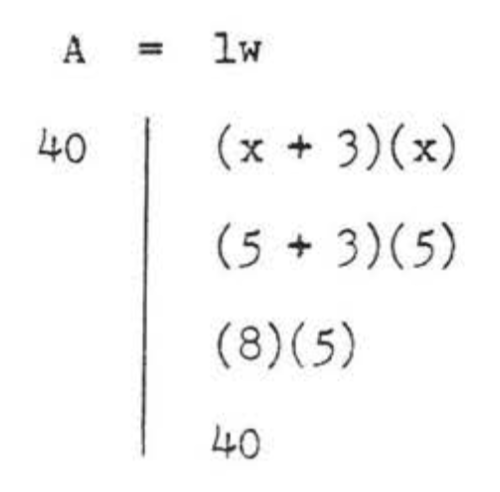
Answer: \(x = 5\).
An L-shaped room has the dimensions indicated in the diagram, How many one by one foot tiles are needed to tile the floor?
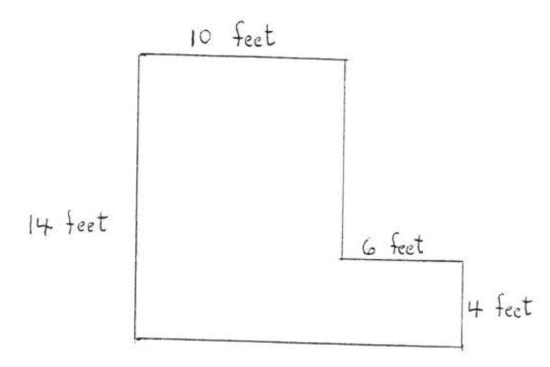
Solution
Divide the room into two rectangles as shown.
\(\begin{array} {rcl} {\text{Area of room}} & = & {\text{Area of large rectangle}} \\ {} & + & {\text{Area of small rectangle}} \\ {} & = & {(14)(10) + (6)(4)} \\ {} & = & {140 + 24} \\ {} & = & {\text{164 square feet.}} \end{array}\)
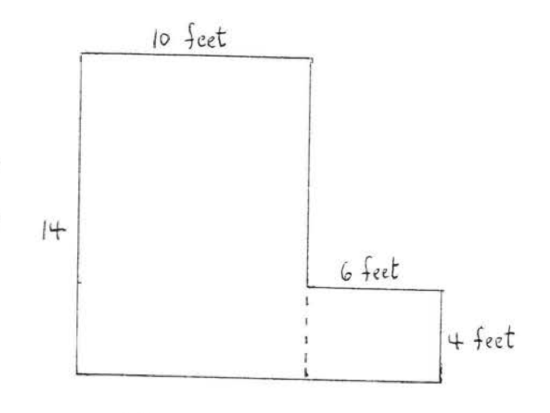
Answer: 164
The need to measu:re land areas was one of the ancient problems which led to the development of geometry. Both the early Egyptians and Babylonians had formulas for the areas of rectangles, triangles, and trapezoids, but some of their formulas were not entirely accurate. The formulas in this chapter were known to the Greeks and are found in Euclid's Elements.
Problems
1 - 14. Find the area and perimeter of \(ABCD\):
1.
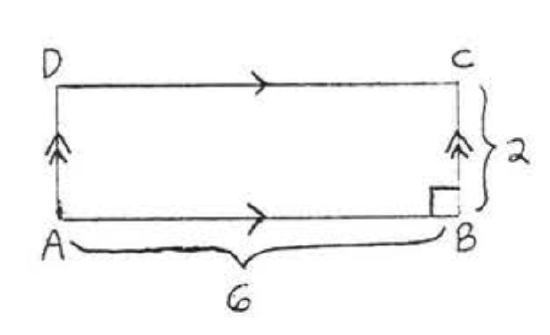
2.
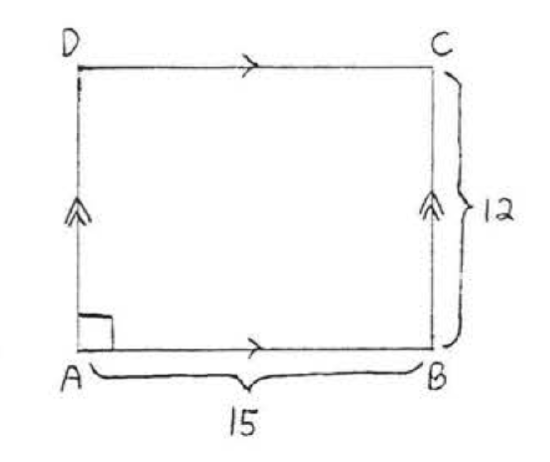
3.
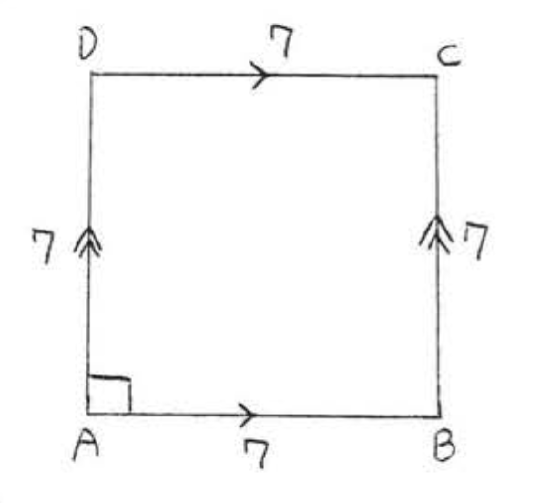
4.
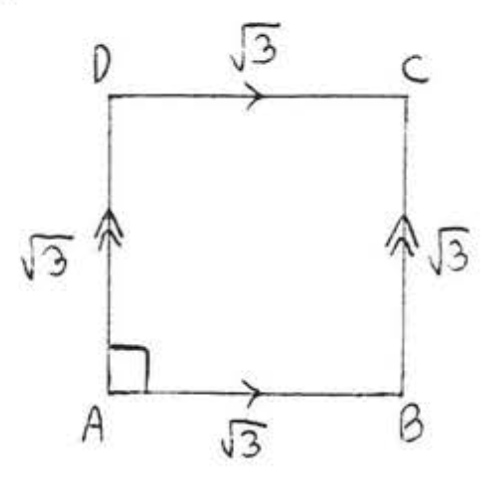
5.
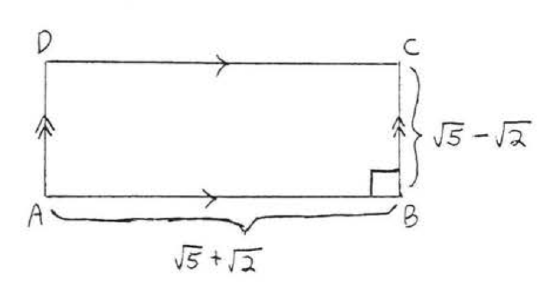
6.
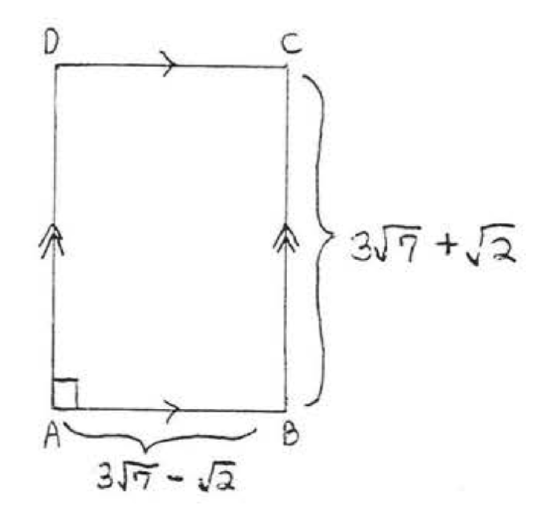
7.
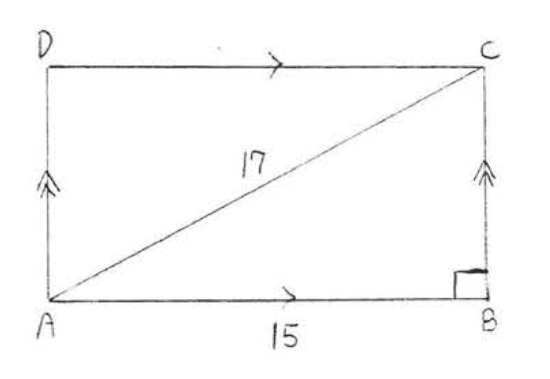
8.
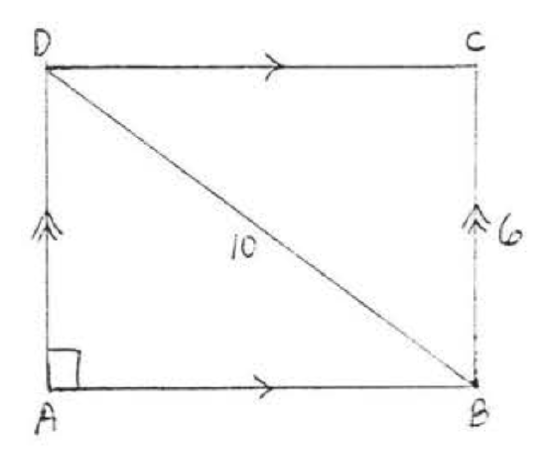
9.
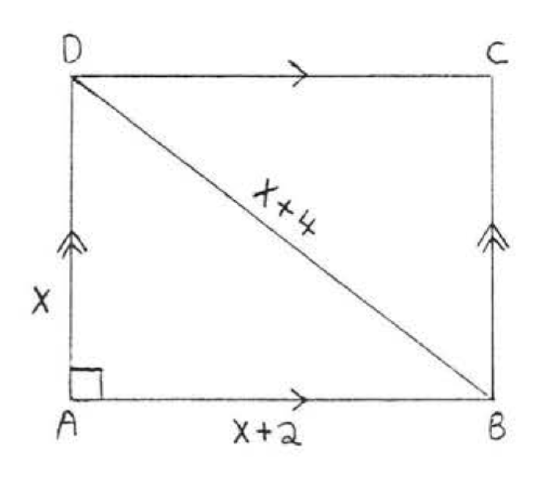
10.
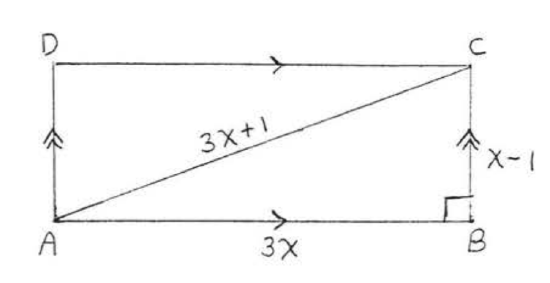
11.
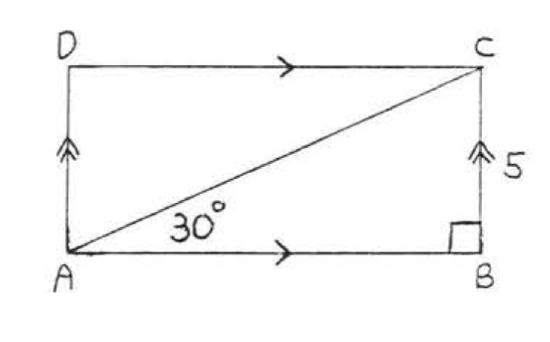
12.
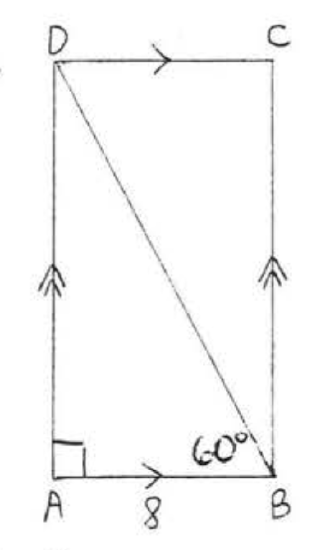
13.
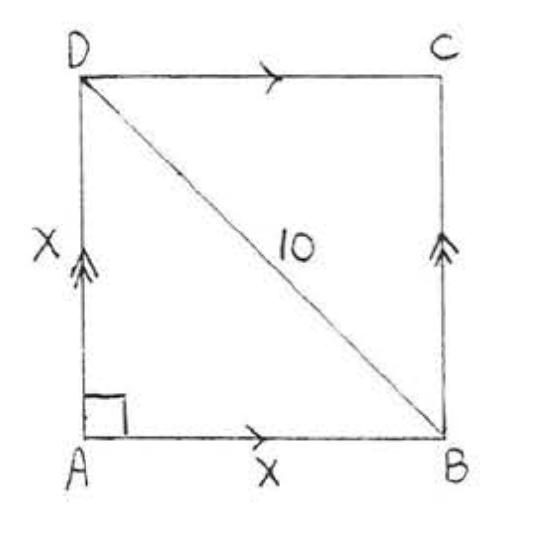
14.
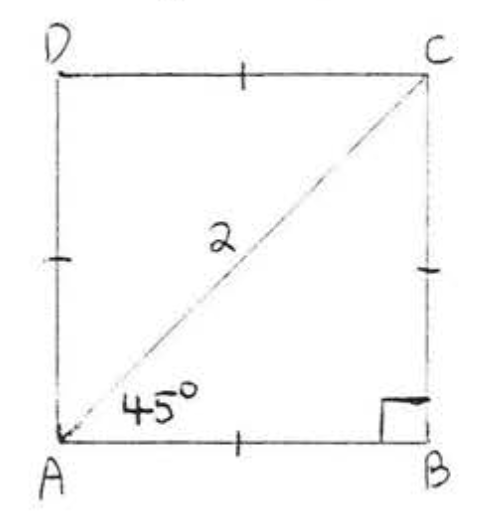
15 - 18. Find \(x\):
15.
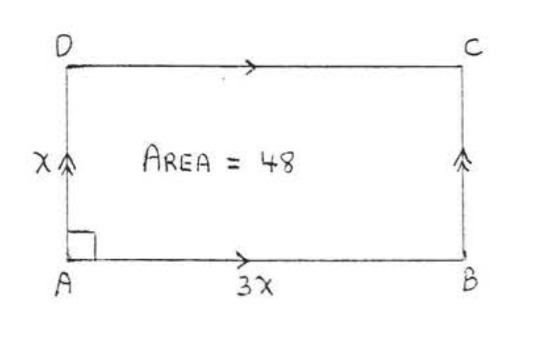
16.
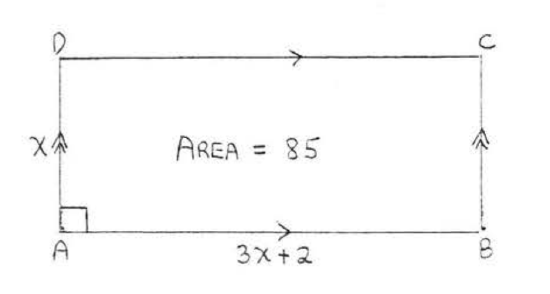
17.
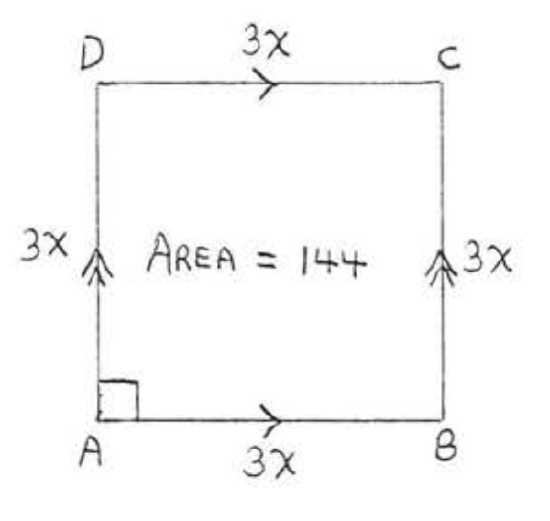
18.
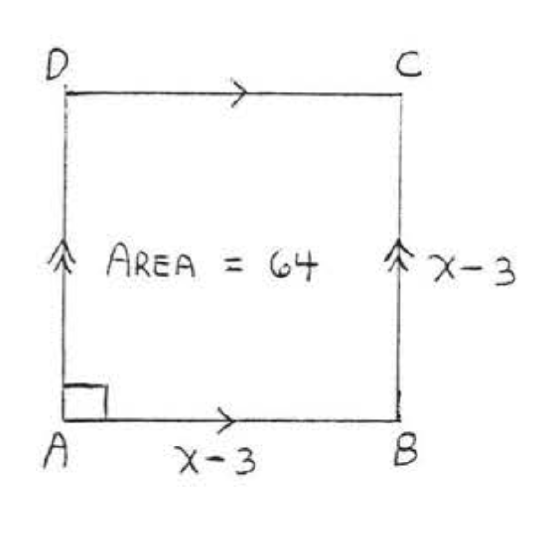
19. A football field has length 300 feet and width 160 feet. What is the area?
20. A tennis court is 78 feet long and 36 feet wide, What is the area?
21 - 24. How many one by one foot tiles are needed to tile each of the following rooms?
21.
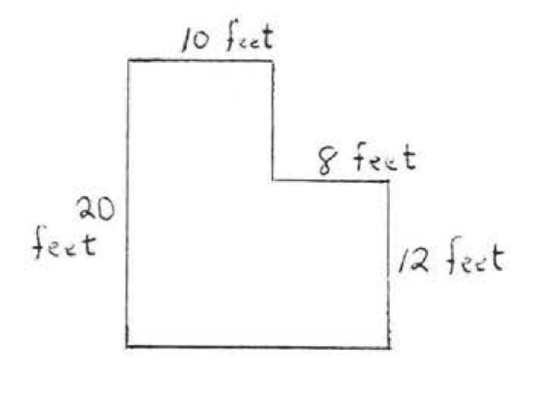
22.
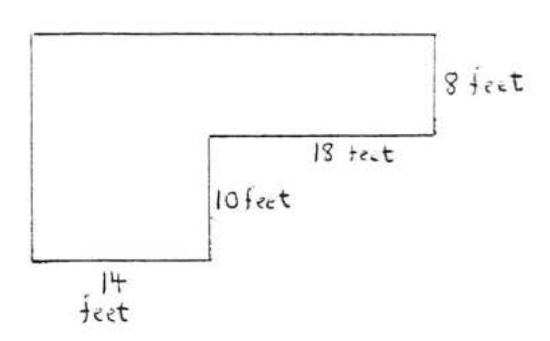
23.
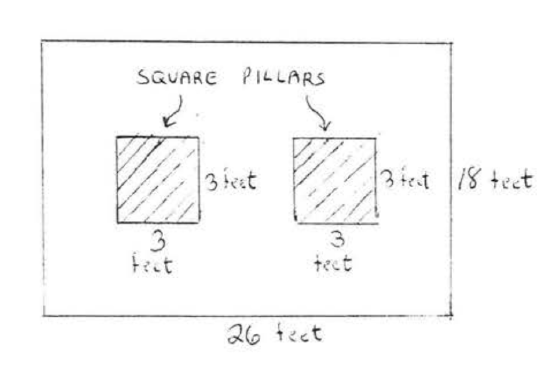
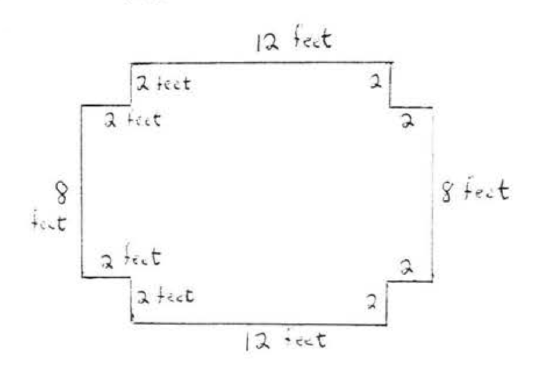
24.
25. A concrete slab weighs 60 pounds per square foot, What is the total weight of a rectangular slab 10 feet long and 3 feet wide?
26. A rectangular piece of plywood is 8 ey 10 feet, If the plywood weighs 3 pounds per square foot, what is the weight of the whole piece?


