7.3: The Area of a Triangle
- Page ID
- 24855
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)For each of the triangles in Figure \(\PageIndex{1}\), side \(AB\) is called the base and \(CD\) is called the height or altitude drawn to this base. The base can be any state of the triangle though it is usually chosen to be the side on which the triangle appears to be resting. The height is the line drawn perpendicular to the base from the opposite vertex. Note that the height may fall outside the triangle, If the triangle is obtuse, and that the height may be one of the legs, if the triangle is a right triangle.
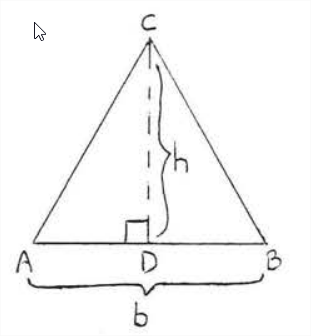
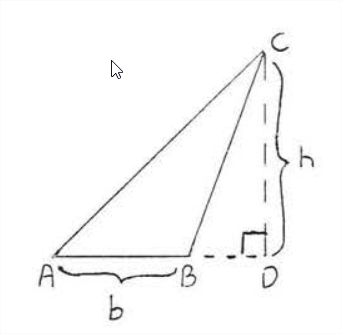
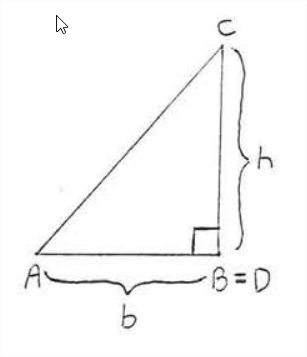
The area of a triangle is equal to one-half of its base times its height.
\[A = \dfrac{1}{2} bh\]
- Proof
-
For each of the triangles illustrated in Figure \(\PageIndex{1}\), draw \(AE\) and \(CE\) so that \(ABCE\) is a parallelogram (Figure \(PageIndex{2}\)). \(\triangle ABC \cong \triangle CEA\) so area of \(\triangle ABC = \text{ area of } \triangle CEA\). Therefore area of \(\triangle ABC = \dfrac{1}{2} \text{ area of parallelogram } ABCE = \dfrac{1}{2} bh\).
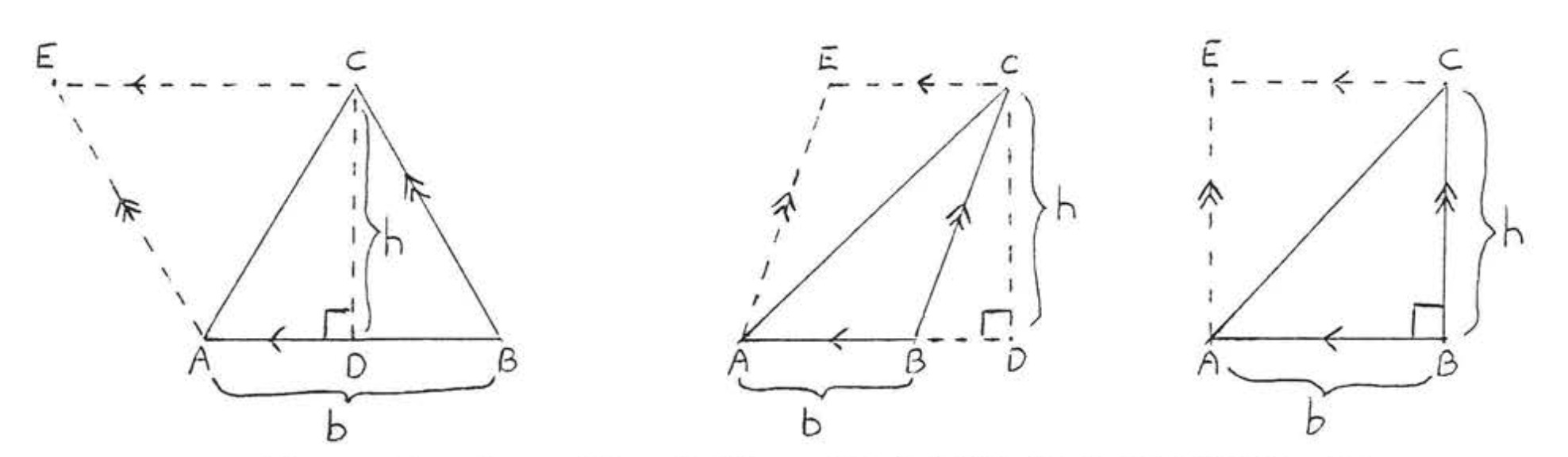 Figure \(\PageIndex{2}\): Draw \(AE\) and \(CE\) so that \(ABCE\) is a parallelogram.
Figure \(\PageIndex{2}\): Draw \(AE\) and \(CE\) so that \(ABCE\) is a parallelogram.
Find the area:
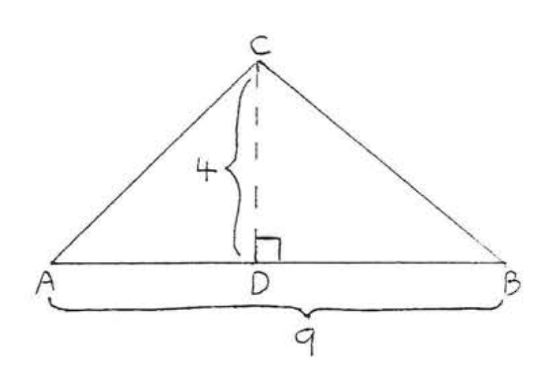
Solution
\(A = \dfrac{1}{2} bh = \dfrac{1}{2} (9) (4) = \dfrac{1}{2} (36) = 18.\)
Answer: 18.
Find the area to the nearest tenth:
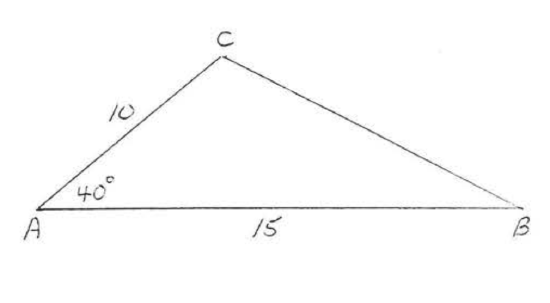
Solution
Draw the height \(h\) as shown in Figure \(\PageIndex{3}\)
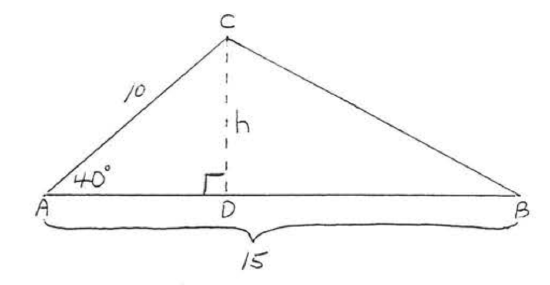 Figure \(\PageIndex{3}\): Draw height \(h\).
Figure \(\PageIndex{3}\): Draw height \(h\).
\[\begin{array} {rcl} {\sin 40^{\circ}} & = & {\dfrac{h}{10}} \\ {.6428} & = & {\dfrac{h}{10}} \\ {(10)(.6428)} & = & {\dfrac{h}{10}(10)} \\ {6.428} & = & {h} \end{array}\]
Area = \(\dfrac{1}{2} bh = \dfrac{1}{2} (15)(6.428) = \dfrac{1}{2} (96.420) = 48.21 = 48.2\)
Answer: \(A = 48.2\)
Find the area and perimeter:
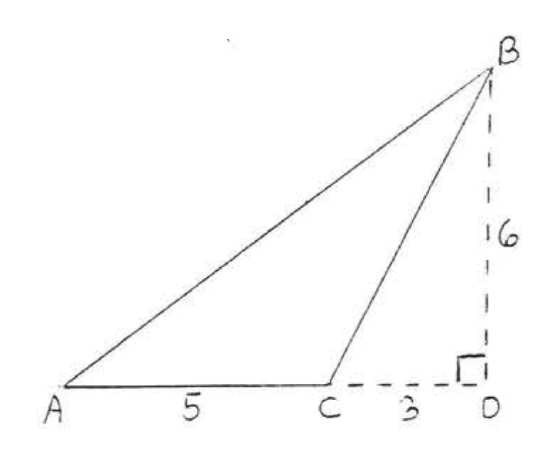
Solution
\(A = \dfrac{1}{2} bh = \dfrac{1}{2} (5)(6) = \dfrac{1}{2} (30) = 15.\)
To find \(AB\) and \(BC\) we use the Pythagorean theorem:
\(\begin{array} {rcl} {\text{AD}^2 + \text{BD}^2} & = & {\text{AB}^2} \\ {8^2 + 6^2} & = & {\text{AB}^2} \\ {64 + 36} & = & {\text{AB}^2} \\ {100} & = & {\text{AB}^2} \\ {10} & = & {\text{AB}} \end{array}\) \(\begin{array} {rcl} {\text{CD}^2 + \text{BD}^2} & = & {\text{BC}^2} \\ {3^2 + 6^2} & = & {\text{BC}^2} \\ {9 + 36} & = & {\text{BC}^2} \\ {45} & = & {\text{BC}^2} \\ {\text{BC} = \sqrt{45}} & = & {\sqrt{9} \sqrt{5} = 3\sqrt{5}} \end{array}\)
Perimeter = \(AB + AC + BC = 10 + 5 + 3\sqrt{5} = 15 + 3 \sqrt{5}\)
Answer: \(A = 15, P = 15 + 3\sqrt{5}\).
Find the area and perimeter:
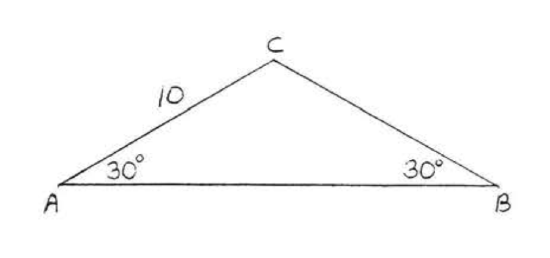
Solution
\(\angle A = \angle B = 30^{\circ}\) so \(\triangle ABC\) is isosceles with \(BC = AC = 10\). Draw height \(h\) as in Figure \(\PageIndex{4}\).
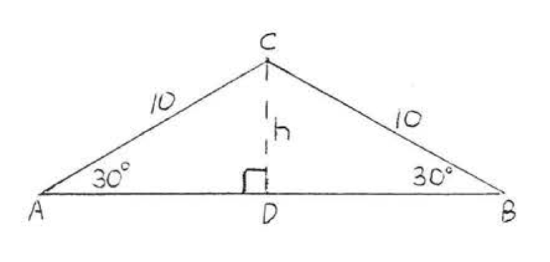 Figure \(\PageIndex{4}\): Draw height \(h\).
Figure \(\PageIndex{4}\): Draw height \(h\).
\(\triangle ACD\) is a \(30^{\circ} - 60^{\circ} -90^{\circ}\) triangle hence
\[\begin{array} {rcl} {\text{hypotenuse}} & = & {2 (\text{short leg})} \\ {10} & = & {2h} \\ {5} & = & {h} \\ {\text{long leg}} & = & {(\text{short leg}) (\sqrt{3})} \\ {AD} & = & {h\sqrt{3} = 5\sqrt{3}.} \end{array} \]
Similarly \(BD = 5\sqrt{3}\).
Area = \(\dfrac{1}{2} bh = \dfrac{1}{2} (5\sqrt{3} + 5\sqrt{3})(5) = \dfrac{1}{2} (10\sqrt{3})(5) = \dfrac{1}{2}(50\sqrt{3}) = 25\sqrt{3}\).
Perimeter = \(10 + 10 + 5\sqrt{3} + 5 \sqrt{3} = 20 + 10 \sqrt{3}\).
Answer: \(A = 25\sqrt{3}, P = 20 + 10 \sqrt{3}\).
Problems
1 - 4. Find the area of \(\triangle ABC\):
1.
2.
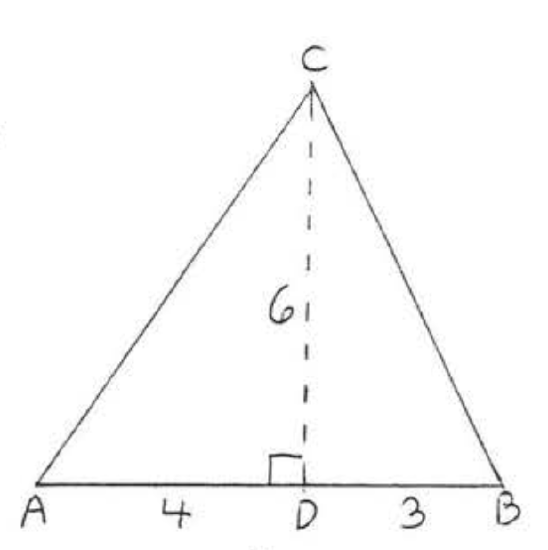
3.
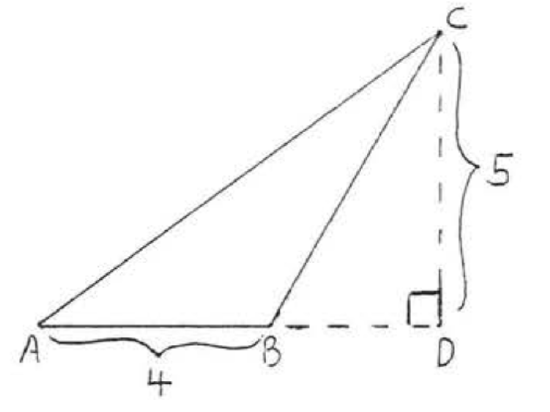
4.
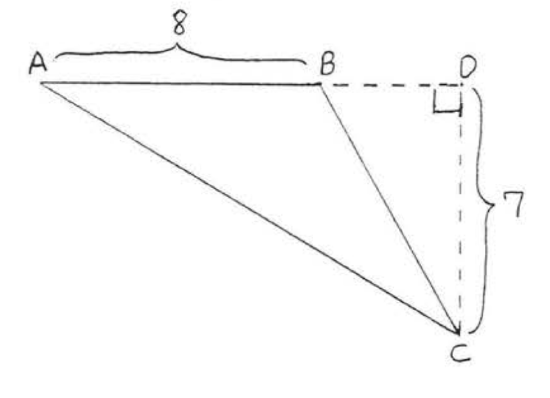
5 - 6. Find the area to the nearest tenth:
5.
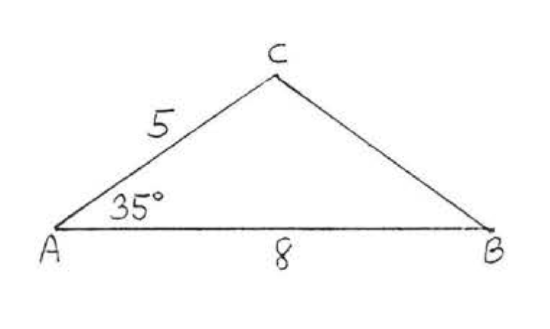
6.
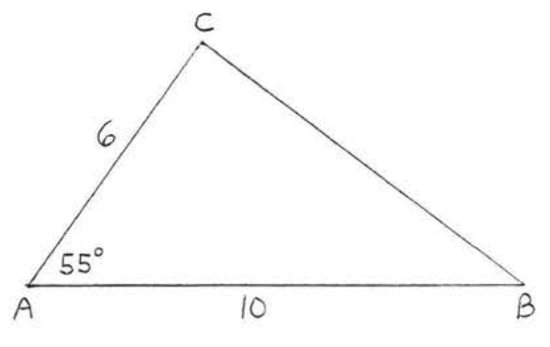
7 - 20. Find the area and perimeter of \(\triangle ABC\):
7.
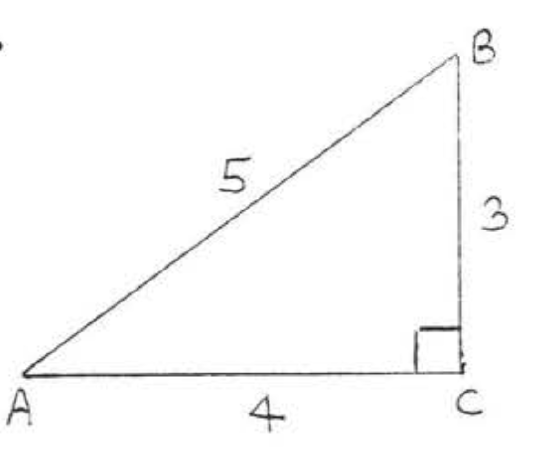
8.
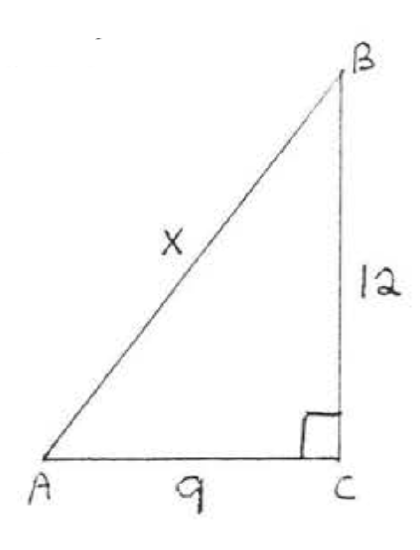
9.
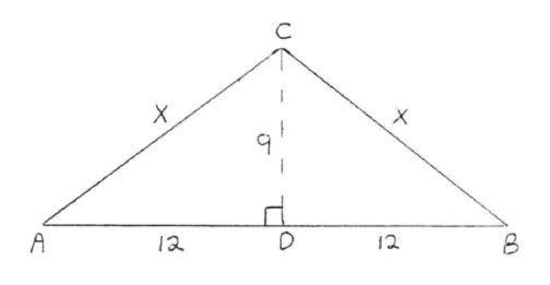
10.
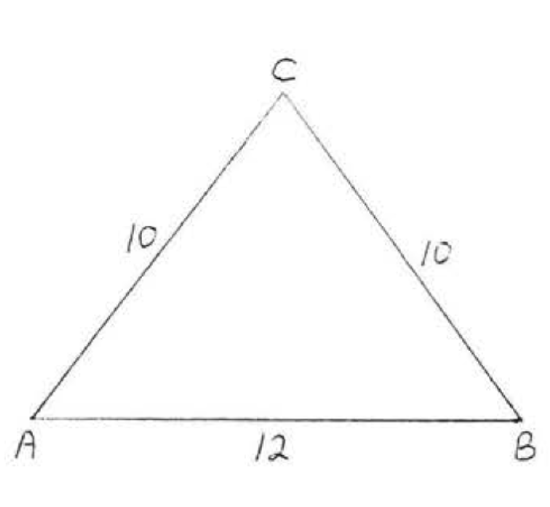
11.
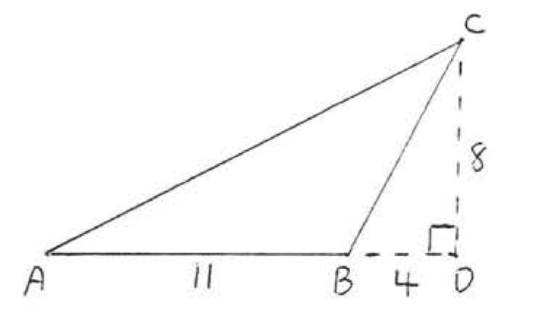
12.
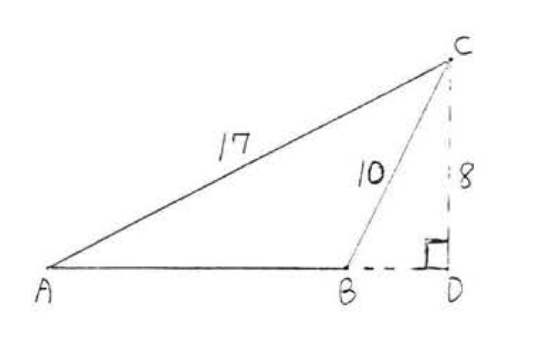
13.
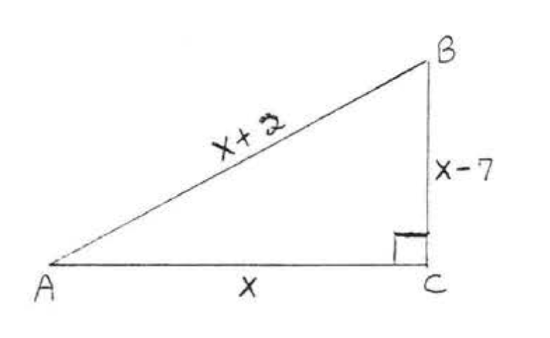
14.
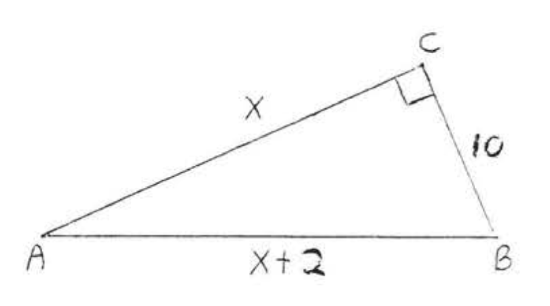
15.
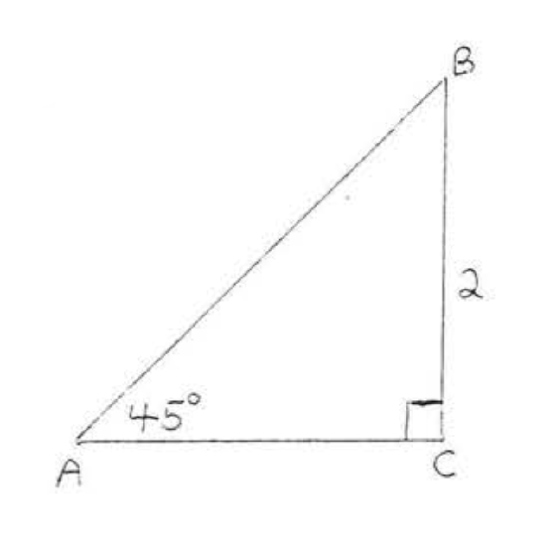
16.
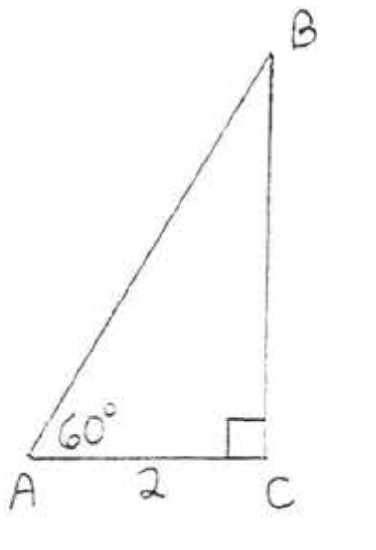
17.
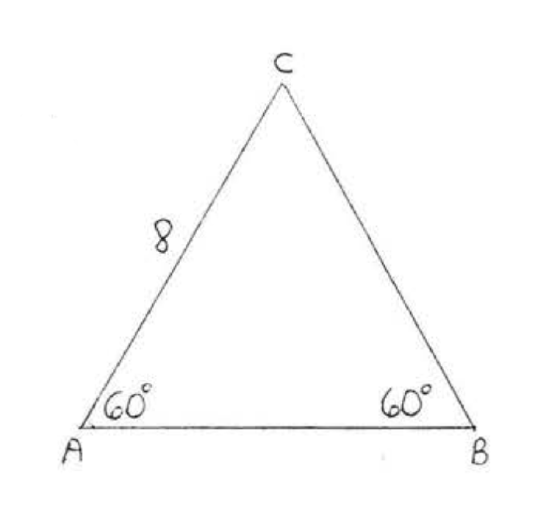
18.
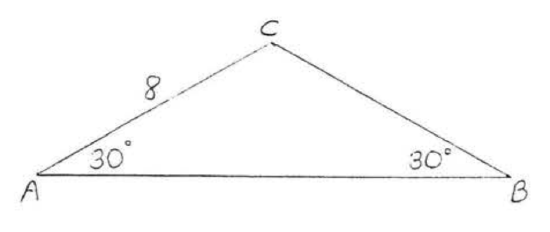
19 - 20. Find the area and perimeter to the nearest tenth:
19.
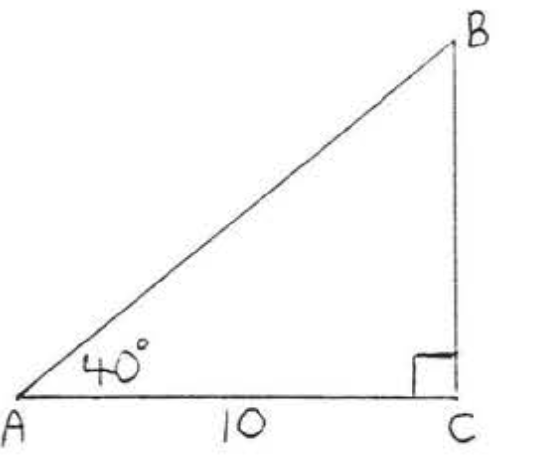
20.
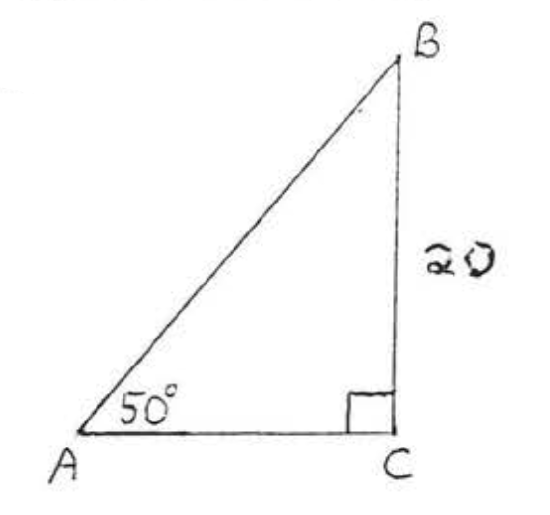
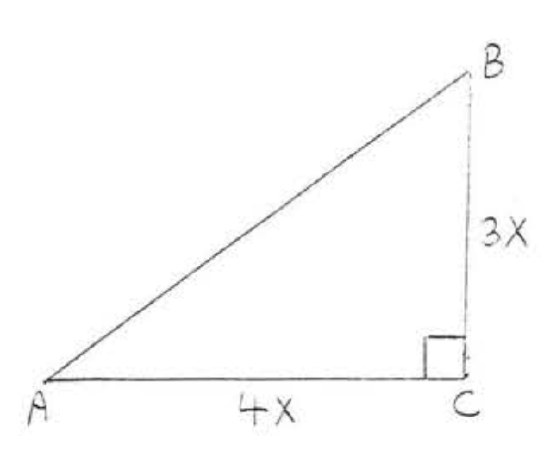
21. Find \(x\) if the area of \(\triangle ABC\) is 35:
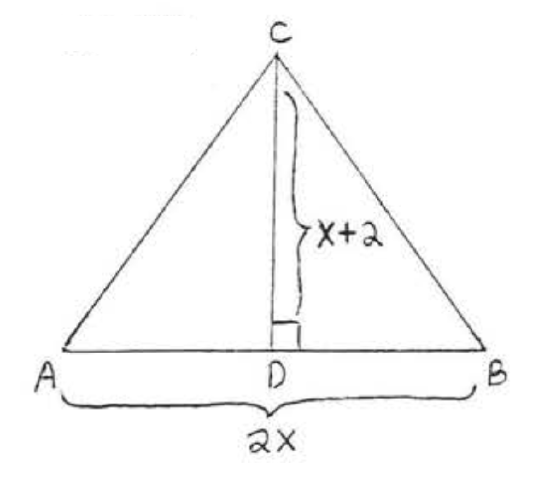
22. Find \(x\) if the area of \(\triangle ABC\) is 24.
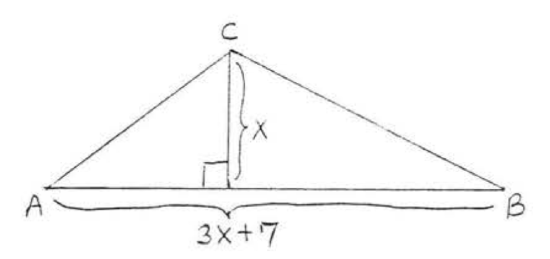
23. Find \(x\) if the area of \(\triangle ABC\) is 12:
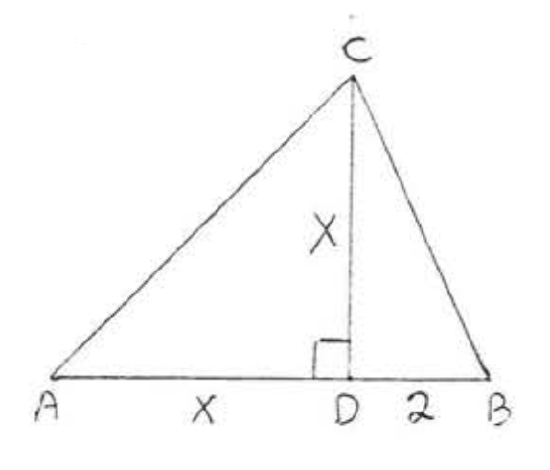
24. Find \(x\) if the area of \(\triangle ABC\) is 108: