7.1: Angles
- Page ID
- 24853
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)An angle is the figure formed by two rays with a common end point, The two rays are called the sides of the angle and the common end point is called the vertex of the angle, The symbol for angle is \(\angle\)
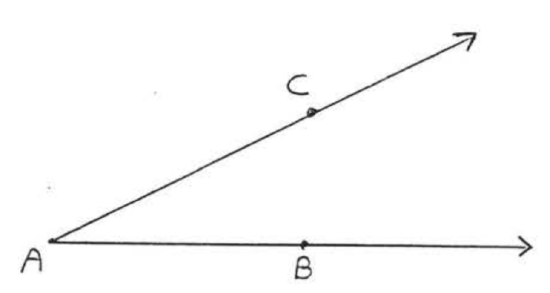 Figure \(\PageIndex{1}\): Angle \(BAC\) has vertex \(A\) and sides \(\overrightarrow{AB}\) and \(\overrightarrow{AC}\)
Figure \(\PageIndex{1}\): Angle \(BAC\) has vertex \(A\) and sides \(\overrightarrow{AB}\) and \(\overrightarrow{AC}\)
The angle in Figure \(\PageIndex{1}\) has vertex \(A\) and sides \(AB\) and \(AC\), It is denoted by \(\angle BAC\) or \(\angle CAB\) or simply \(\angle A\). When three letters are used, the middle letter is always the vertex, In Figure \(\PageIndex{2}\) we would not use the notation \(\angle A\) as an abbreviation for \(\angle BAC\) because it could also mean \(\angle CAD\) or \(\angle BAD\), We could however use the simpler name \(\angle x\) for \(\angle BAC\) if "\(x\)" is marked in as shown,
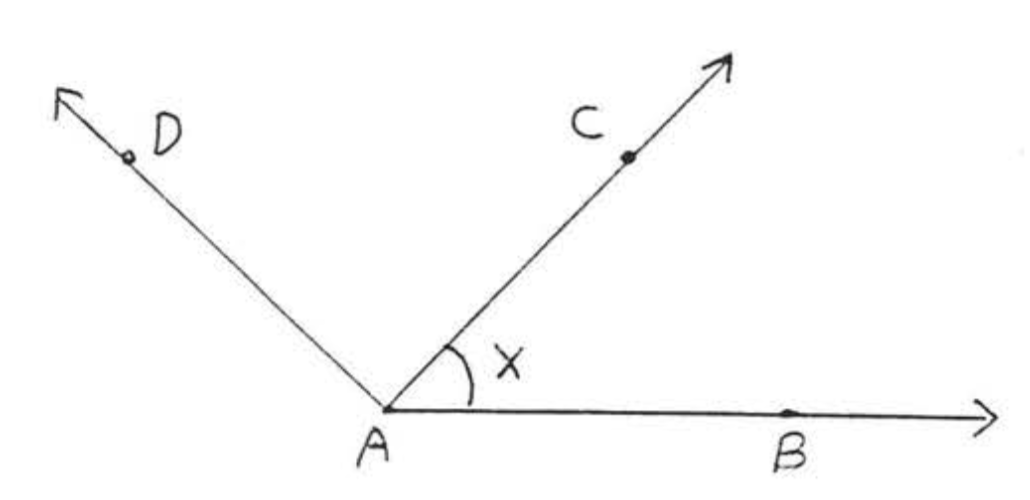 Figure \(\PageIndex{2}\): \(\angle BAC\) may also be denoted by \(\angle x\).
Figure \(\PageIndex{2}\): \(\angle BAC\) may also be denoted by \(\angle x\).
Angles can be measured with an instrument called a protractor. The unit of measurement is called a degree and the symbol for degree is \(^{\circ}\).
To measure an angle, place the center of the protractor (often marked with a cross or a small circle) on the vertex of the angle, Position the protractor so that one side of the angle cuts across 0, at the beginning of the scale, and so that the other side cuts across a point further up on the scale, We use either the upper scale or the lower scale, whichever is more convenient, For example, in Figure \(\PageIndex{3}\), one side of \(\angle BAC\) crosses 0 on the lower scale and the other side crosses 50 on the lower scale. The measure of \(\angle BAC\) is therefore \(50^{\circ}\) and we write \(\angle BAC\) = \(50^{\circ}\).
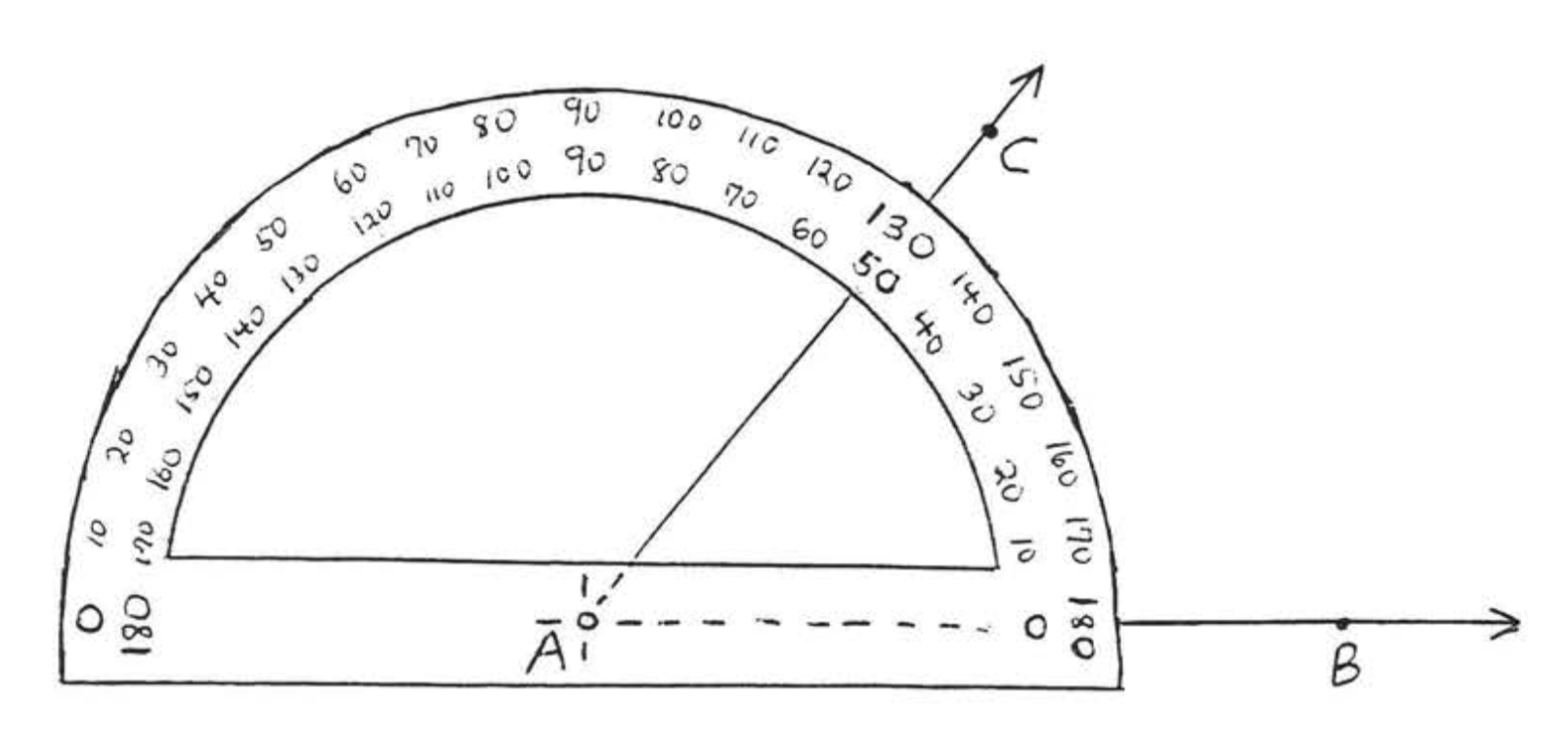 Figure \(\PageIndex{3}\): The protractor shows \(\angle BAC = 50^{\circ}\)
Figure \(\PageIndex{3}\): The protractor shows \(\angle BAC = 50^{\circ}\)
In Figure \(\PageIndex{4}\), side \(\overrightarrow AD\) of \(\angle DAC\) crosses 0 on the upper scale. Therefore we look on the upper scale for the point at which \(\overrightarrow{AC}\) crosses and conclude that \(\angle DAC = 130^{\circ}\).
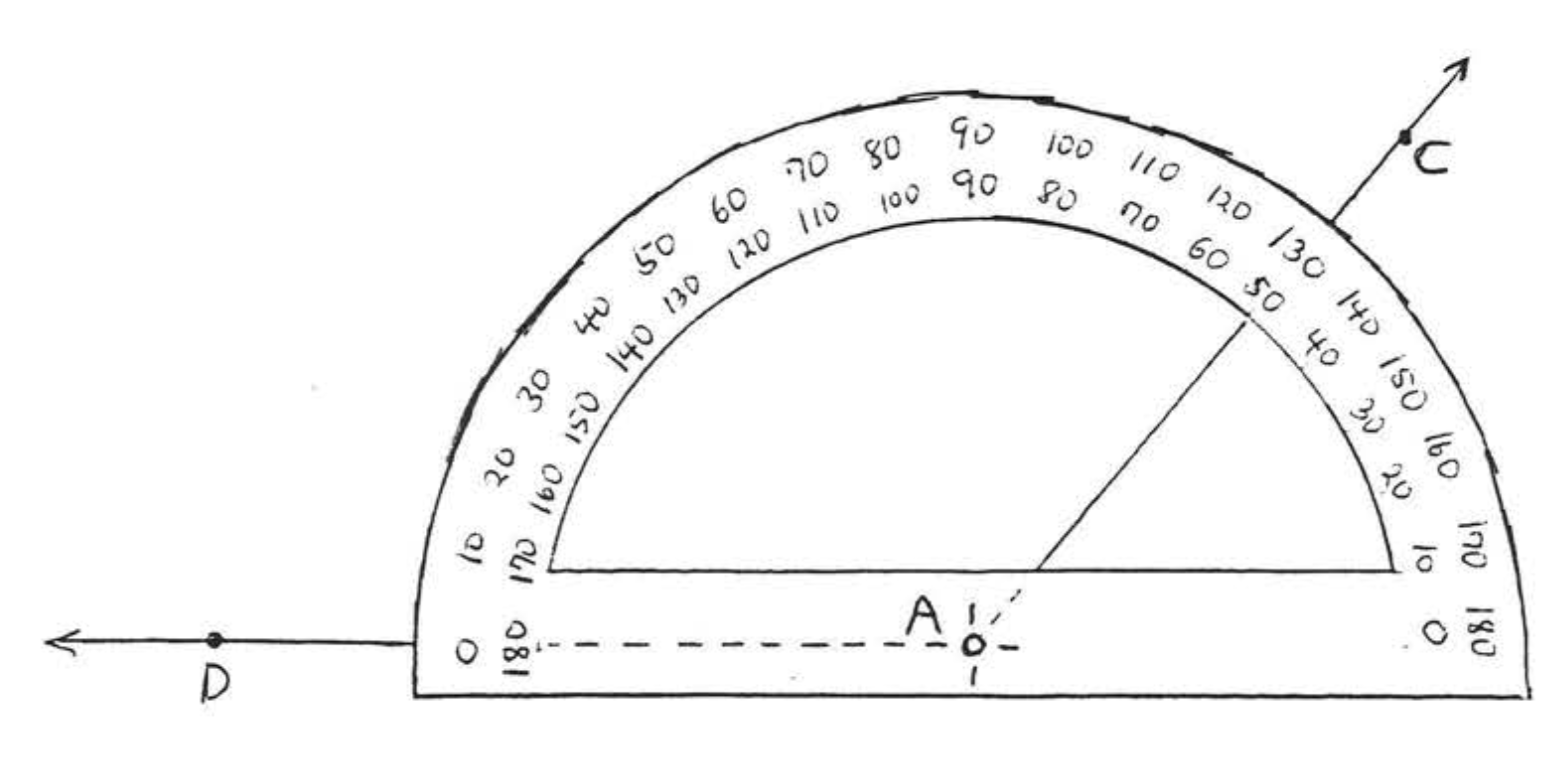 Figure \(\PageIndex{4}\): \(\angle DAC = 130^{\circ}\).
Figure \(\PageIndex{4}\): \(\angle DAC = 130^{\circ}\).
Draw an angle of \(40^{\circ}\) and label it \(\angle BAC\).
Solution
Draw ray \(\overrightarrow{AB}\) using a straight edge:

Place the protractor so that its center coincides with \(A\) and \(\overrightarrow{AB}\) crosses the scale at 0:
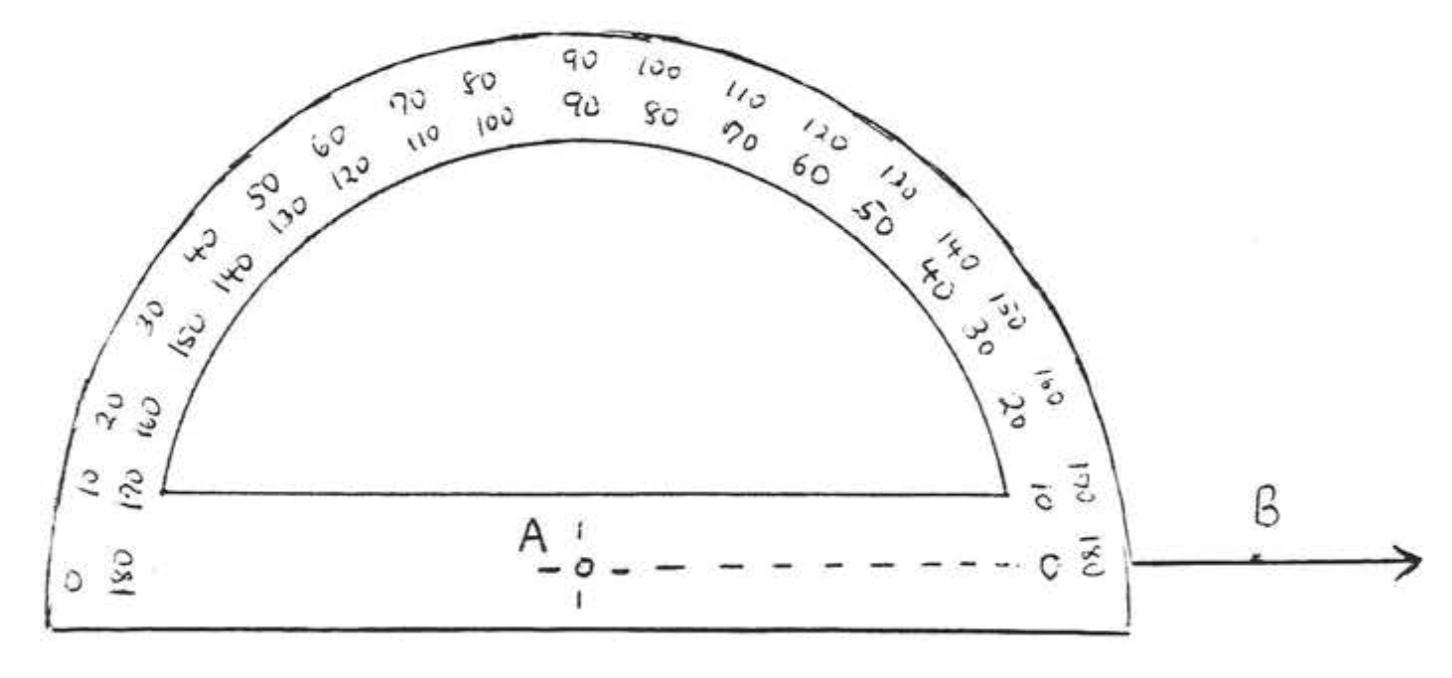
Mark the place on the protractor corresponding to \(40^{\circ}\). Label this point \(C\):
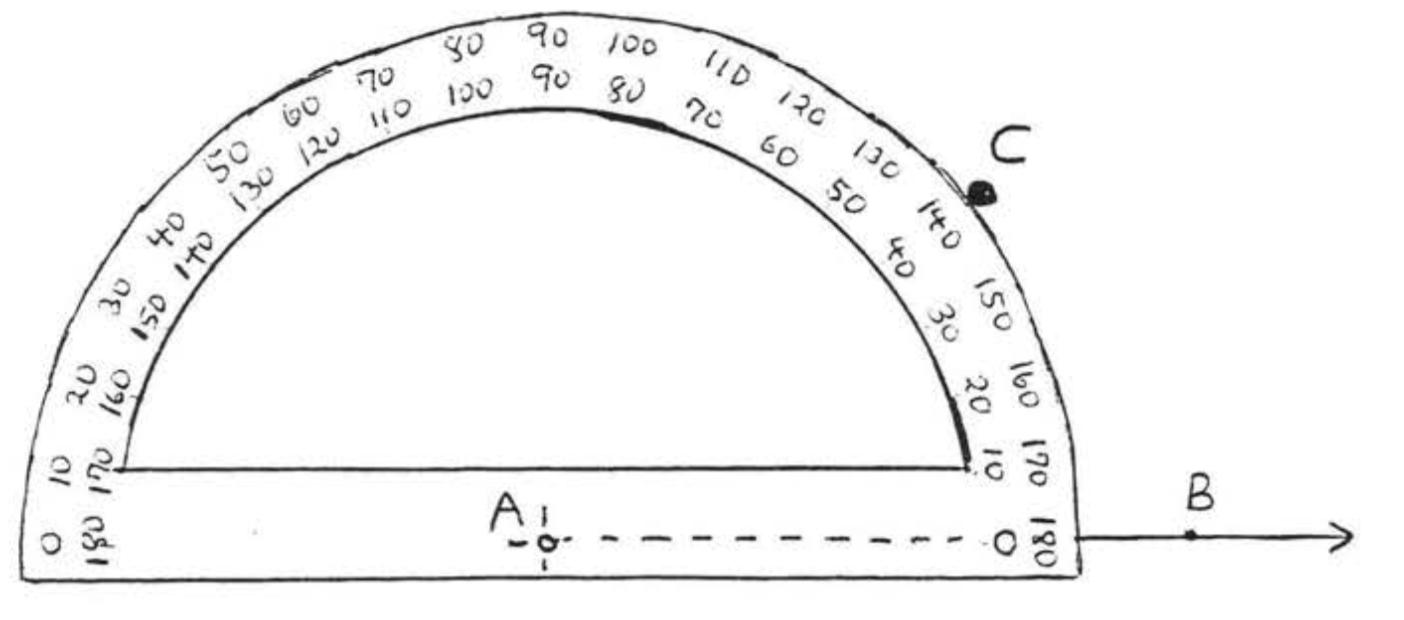
Connect \(A\) with \(C\):
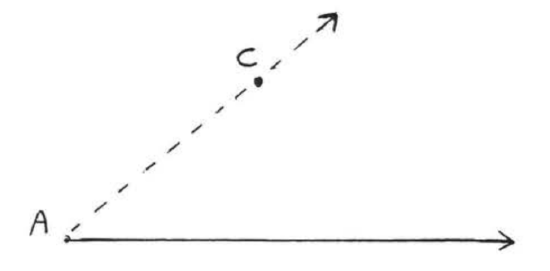
Two angles are said to be equal if they have the same measure in degrees. We often indicate two angles are equal by marking them in the same way. In Figure \(\PageIndex{5}\), \(\angle A = \angle B\).
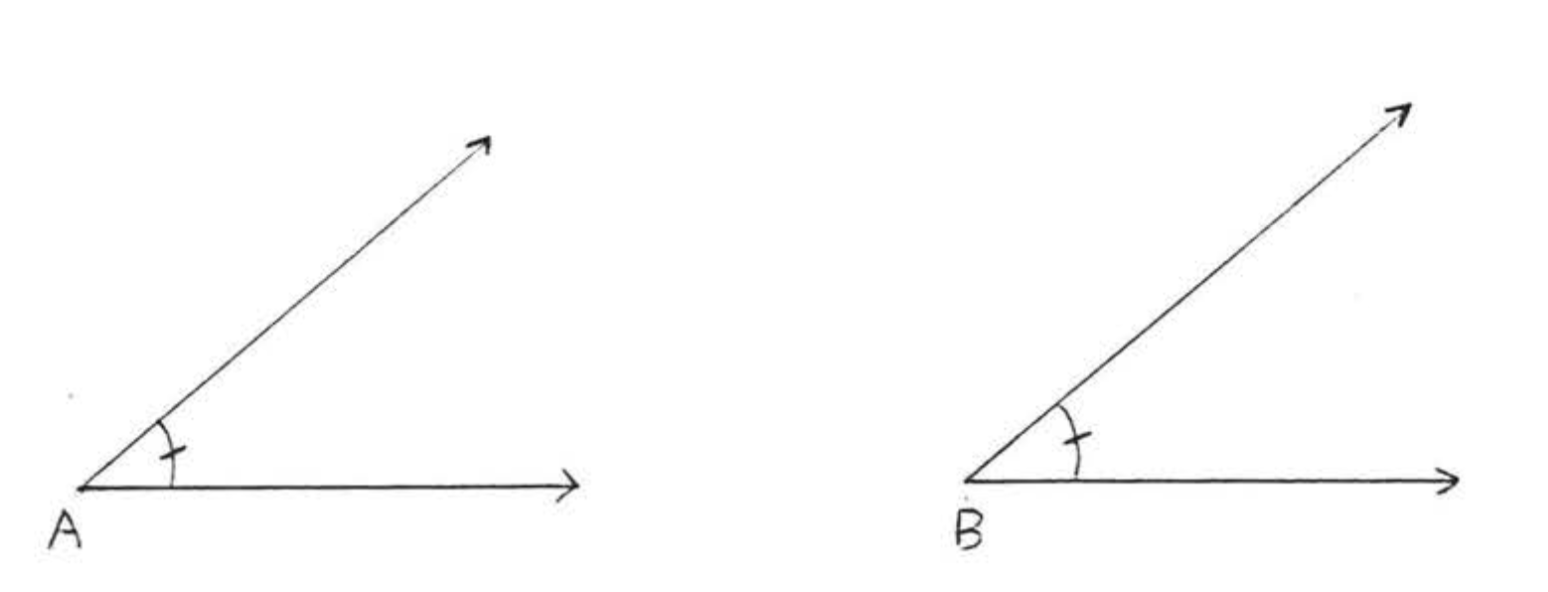 Figure \(\PageIndex{5}\): Equal angles.
Figure \(\PageIndex{5}\): Equal angles.
An angle bisector is a ray which divides an angle into two equal angles. In Figure \(\PageIndex{6}\), \(\overrightarrow{AC}\) is an angle bisector of \(\angle BAD\). We also say \(\overrightarrow{AC}\) bisects \(\angle BAD\).
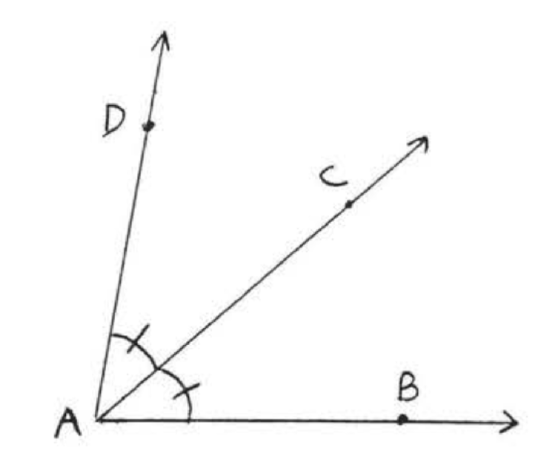 Figure \(\PageIndex{6}\): \(\overrightarrow{AC}\) bisects \(\angle BAD\).
Figure \(\PageIndex{6}\): \(\overrightarrow{AC}\) bisects \(\angle BAD\).
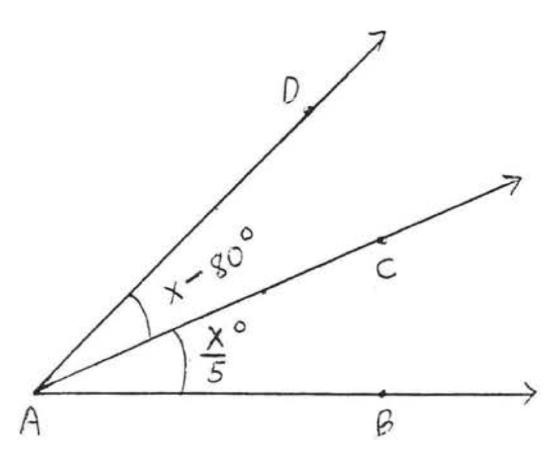
Find \(x\) if \(\overrightarrow{AC}\) bisects \(\angle BAD\) and \(\angle BAD = 80^{\circ}\):
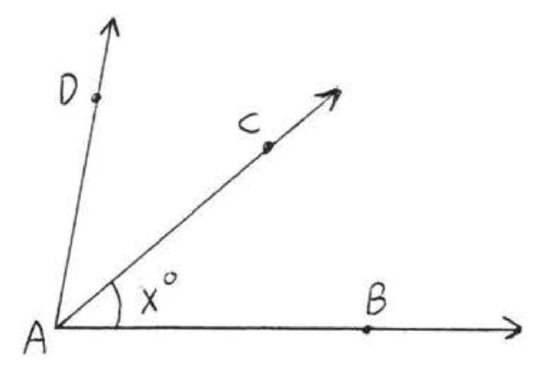
Solution
\(x^{\circ} = \dfrac{1}{2} \angle BAD = \dfrac{1}{2} (80^{\circ}) = 40^{\circ}\)
Answer: \(x = 40\).
Find \(x\) if \(\overrightarrow{AC}\) bisects \(\angle BAD\):
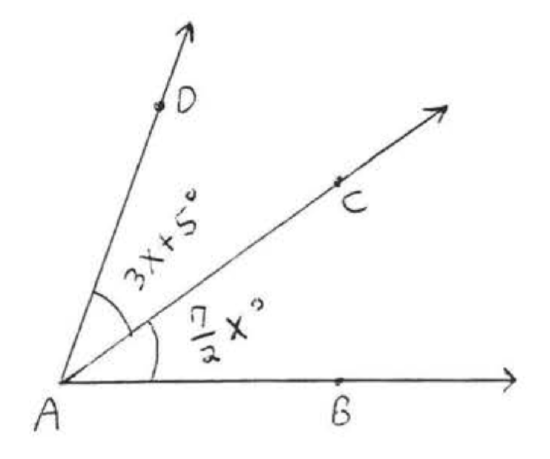
Solution
\[\begin{array} {rcl} {\angle BAC} & = & {\angle CAD} \\ {\dfrac{7}{2} x} & = & {3x + 5} \\ {(2) \dfrac{7}{2} x} & = & {(2) (3x + 5)} \\ {7x} & = & {6x + 10} \\ {7x - 6x} & = & {10} \\ {x } & = & {10} \end{array}\]
Check:
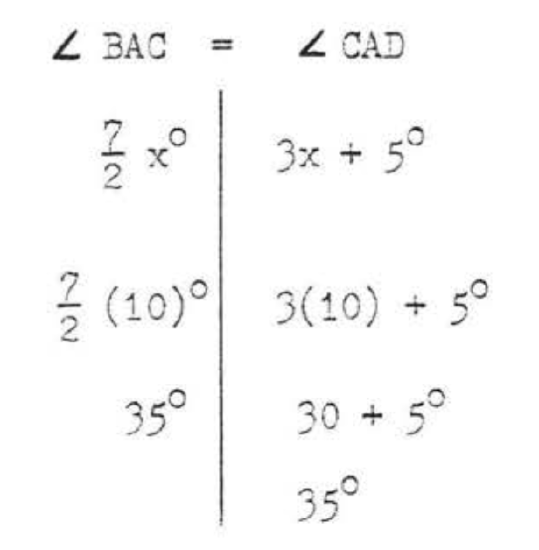
Answer: \(x = 10\).
Problems
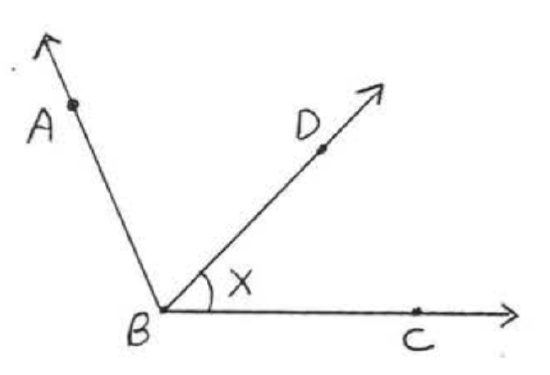
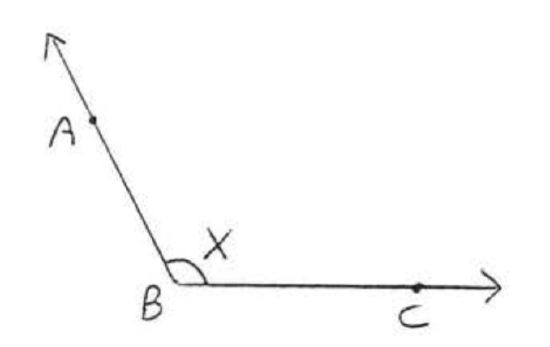
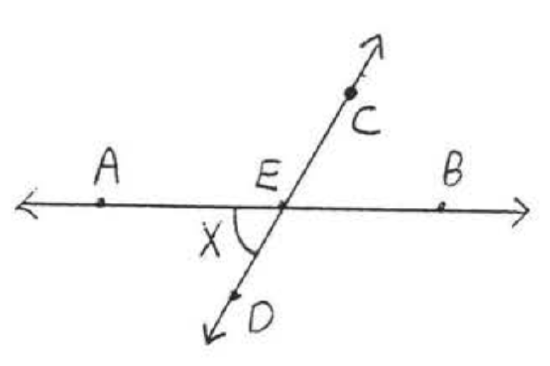
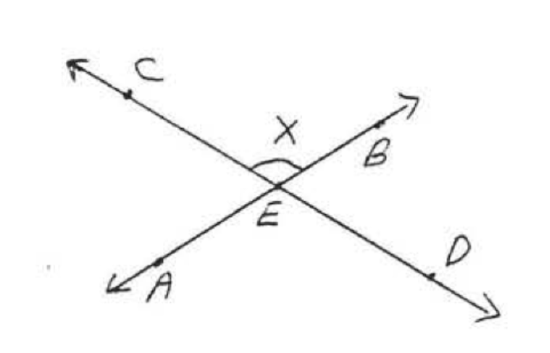
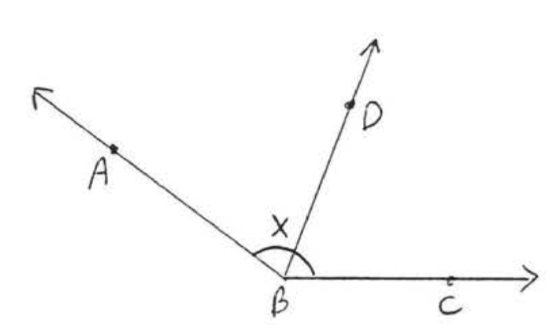
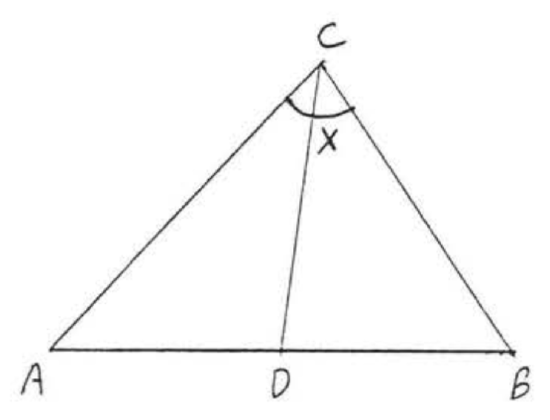
1 - 6. For each figure, give another name for \(\angle x\):
1. 
2. 
3. 
4. 
5. 
6. 
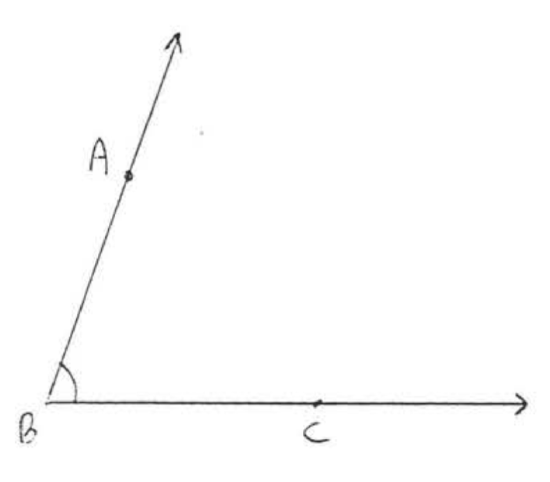
7 - 16, Measure each of the indicated angles:
7. 
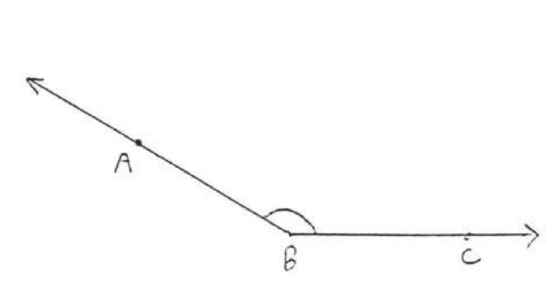
8. 
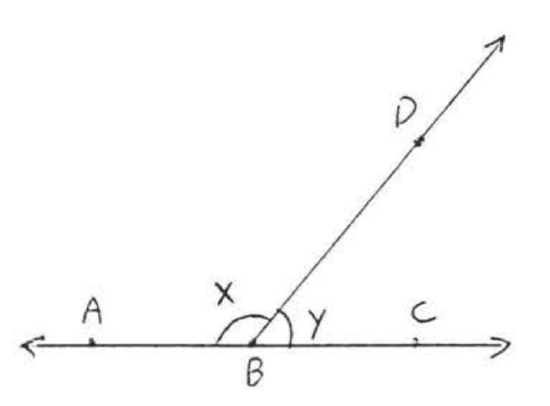
9. 
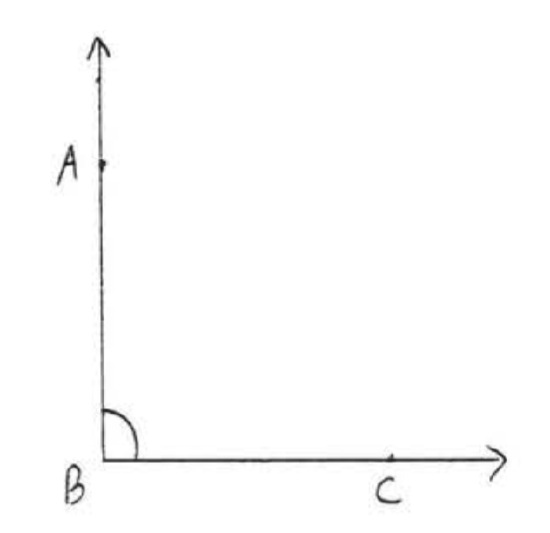
10. 
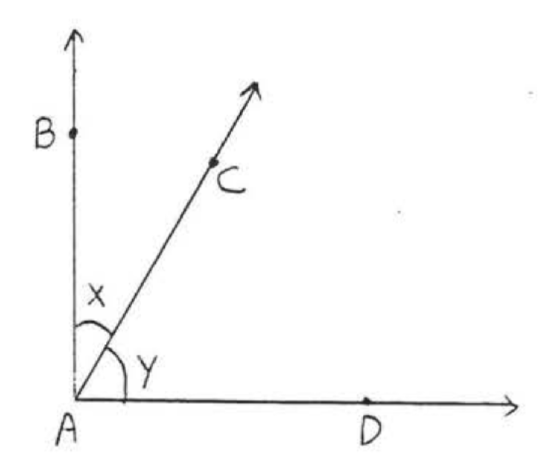
11. 
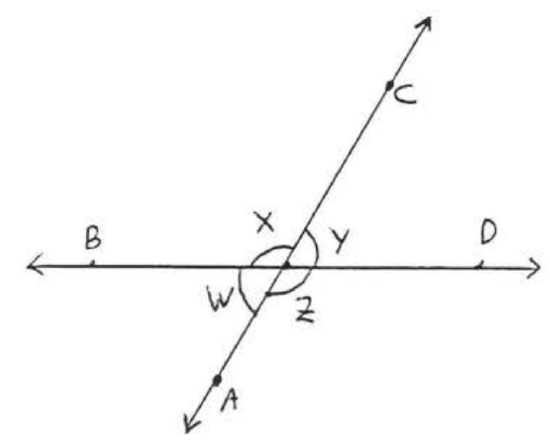
12. 
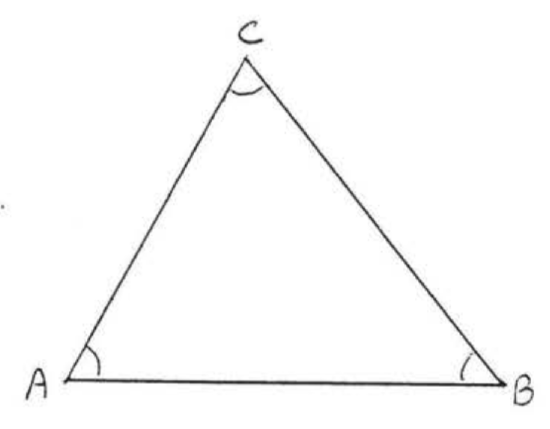
13. 
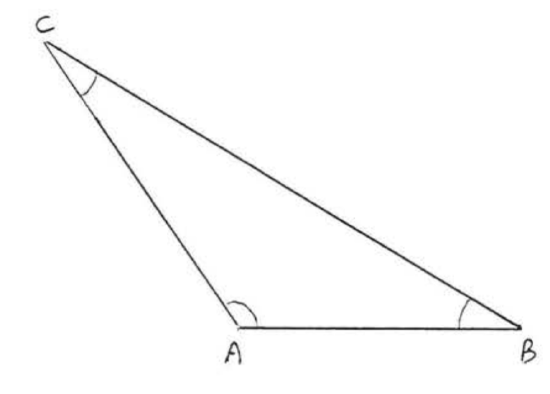
14. 
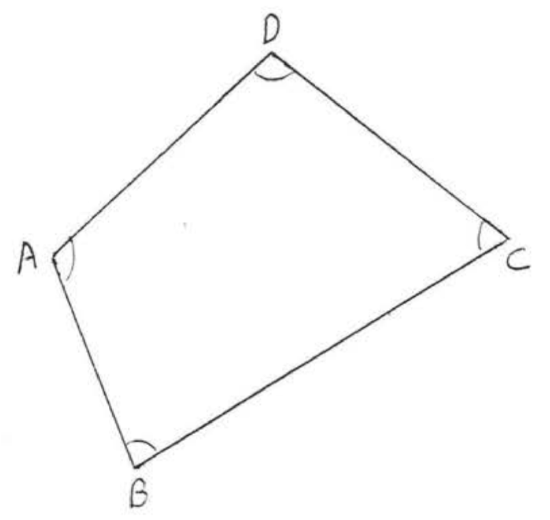
15. 
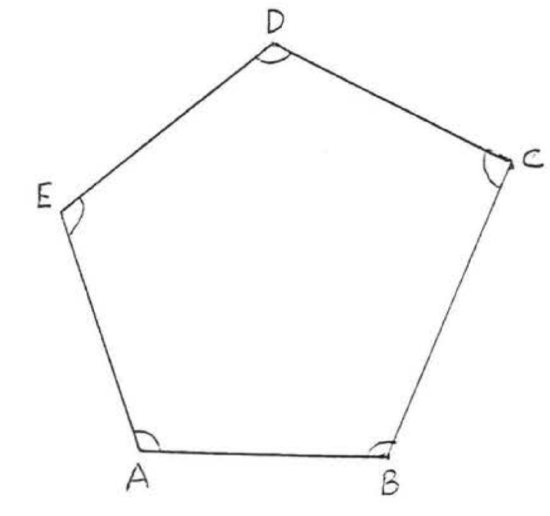
16. 
17 - 24. Draw and label each angle:
17. \(\angle BAC = 30^{\circ}\)
18. \(\angle BAC = 40^{\circ}\)
19. \(\angle ABC = 45^{\circ}\)
20. \(\angle EFG = 60^{\circ}\)
21. \(\angle RST = 72^{\circ}\)
22. \(\angle XYZ = 90^{\circ}\)
23. \(\angle PQR = 135^{\circ}\)
24. \(\angle JKL = 164^{\circ}\)
25 - 28. Find \(x\) if \(\overrightarrow{AC}\) bisects \(\angle BAD\):
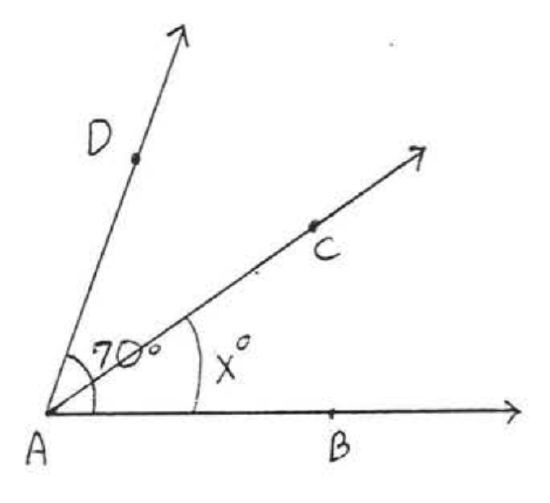
25. 
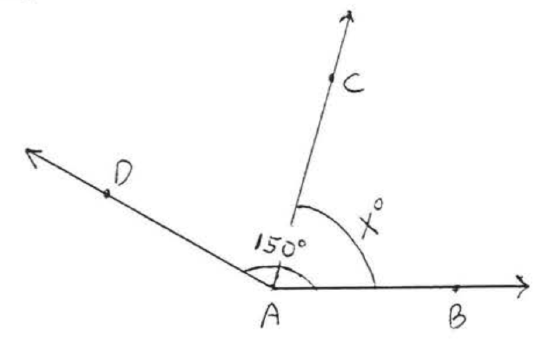
26. 
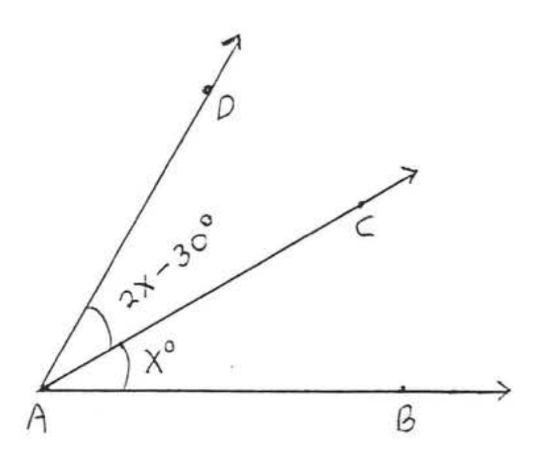
27. 
28.