6.1: Random Variables and Probabilities
- Page ID
- 10857
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Probability associates with an event a number which indicates the likelihood of the occurrence of that event on any trial. An event is modeled as the set of those possible outcomes of an experiment which satisfy a property or proposition characterizing the event.
Often, each outcome is characterized by a number. The experiment is performed. If the outcome is observed as a physical quantity, the size of that quantity (in prescribed units) is the entity actually observed. In many nonnumerical cases, it is convenient to assign a number to each outcome. For example, in a coin flipping experiment, a “head” may be represented by a 1 and a “tail” by a 0. In a Bernoulli trial, a success may be represented by a 1 and a failure by a 0. In a sequence of trials, we may be interested in the number of successes in a sequence of \(n\) component trials. One could assign a distinct number to each card in a deck of playing cards. Observations of the result of selecting a card could be recorded in terms of individual numbers. In each case, the associated number becomes a property of the outcome.
Random variables as functions
We consider in this chapter real random variables (i.e., real-valued random variables). In the chapter on Random Vectors and Joint Distributions, we extend the notion to vector-valued random quantites. The fundamental idea of a real random variable is the assignment of a real number to each elementary outcome \(\omega\) in the basic space \(\Omega\). Such an assignment amounts to determining a function \(X\), whose domain is \(\Omega\) and whose range is a subset of the real line R. Recall that a real-valued function on a domain (say an interval \(I\) on the real line) is characterized by the assignment of a real number \(y\) to each element \(x\) (argument) in the domain. For a real-valued function of a real variable, it is often possible to write a formula or otherwise state a rule describing the assignment of the value to each argument. Except in special cases, we cannot write a formula for a random variable \(X\). However, random variables share some important general properties of functions which play an essential role in determining their usefulness.
Mappings and inverse mappings
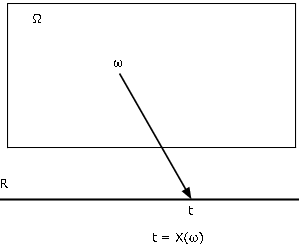
There are various ways of characterizing a function. Probably the most useful for our purposes is as a mapping from the domain \(\Omega\) to the codomain R. We find the mapping diagram of Figure 1 extremely useful in visualizing the essential patterns. Random variable \(X\), as a mapping from basic space \(\Omega\) to the real line R, assigns to each element \(\omega\) a value \(t = X(\omega)\). The object point \(\omega\) is mapped, or carried, into the image point \(t\). Each \(\omega\) is mapped into exactly one \(t\), although several \(\omega\) may have the same image point.
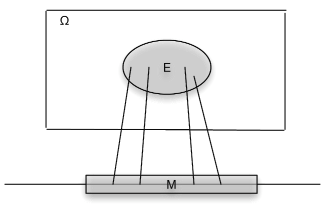
Associated with a function \(X\) as a mapping are the inverse mapping \(X^{-1}\) and the inverse images it produces. Let \(M\) be a set of numbers on the real line. By the inverse image of \(M\) under the mapping \(X\), we mean the set of all those \(\omega \in \Omega\) which are mapped into \(M\) by \(X\) (see Figure 2). If \(X\) does not take a value in \(M\), the inverse image is the empty set (impossible event). If \(M\) includes the range of \(X\), (the set of all possible values of \(X\)), the inverse image is the entire basic space \(\Omega\). Formally we write
\(X^{-1} (M) = \{\omega: X(\omega) \in M\}\)
Now we assume the set \(X^{-1} (M)\), a subset of \(\Omega\), is an event for each \(M\). A detailed examination of that assertion is a topic in measure theory. Fortunately, the results of measure theory ensure that we may make the assumption for any \(X\) and any subset \(M\) of the real line likely to be encountered in practice. The set \(X^{-1} (M)\) is the event that \(X\) takes a value in \(M\). As an event, it may be assigned a probability.
Example \(\PageIndex{1}\) Some illustrative examples
- \(I_E\) where \(E\) is an event with probability \(p\). Now \(X\) takes on only two values, 0 and 1. The event that \(X\) take on the value 1 is the set
\(\{\omega: X(\omega) = 1\} = X^{-1} (\{1\}) = E\)
so that \(P(\{\omega: X(\omega) = 1\}) = p\). This rather ungainly notation is shortened to \(P(X = 1) = p\). Similarly, . Consider any set \(M\). If neither 1 nor 0 is in \(M\), then \(X^{-1}(M) = \emptyset\) If 0 is in \(M\), but 1 is not, then \(X^{-1} (M) = E^c\) If 1 is in \(M\), but 0 is not, then \(X^{-1} (M) = E\) If both 1 and 0 are in \(M\), then \(X^{-1} (M) = \Omega\) In this case the class of all events \(X^{-1} (M)\) consists of event \(E\), its complement \(E^c\), the impossible event \(\emptyset\), and the sure event \(\Omega\). - Consider a sequence of \(n\) Bernoulli trials, with probability \(p\) of success. Let \(S_n\) be the random variable whose value is the number of successes in the sequence of \(n\) component trials. Then, according to the analysis in the section "Bernoulli Trials and the Binomial Distribution"
\(P(S_n = k) = C(n, k) p^k (1-p)^{n - k}\) \(0 \le k \le n\)
Before considering further examples, we note a general property of inverse images. We state it in terms of a random variable, which maps \(\Omega\) to the real line (see Figure 3).
Preservation of set operations
Let \(X\) be a mapping from \(\Omega\) to the real line R. If \(M, M_i, i \in J\) are sets of real numbers, with respective inverse images \(E\), \(E_i\), then
\(X^{-1} (M^c) = E^c\), \(X^{-1} (\bigcup_{i \in J} M_i) = \bigcup_{i \in J} E_i\) and \(X^{-1} (\bigcap_{i \in J} M_i) = \bigcap_{i \in J} E_i\)
Examination of simple graphical examples exhibits the plausibility of these patterns. Formal proofs amount to careful reading of the notation. Central to the structure are the facts that each element ω is mapped into only one image point t and that the inverse image of \(M\) is the set of all those \(\omega\) which are mapped into image points in \(M\).
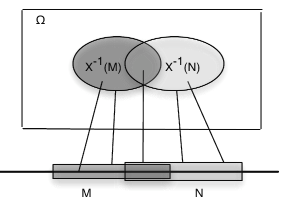
An easy, but important, consequence of the general patterns is that the inverse images of disjoint \(M, N\) are also disjoint. This implies that the inverse of a disjoint union of \(M_i\) is a disjoint union of the separate inverse images.
Example \(\PageIndex{2}\) Events determined by a random variable
Consider, again, the random variable \(S_n\) which counts the number of successes in a sequence of \(n\) Bernoulli trials. Let \(n = 10\) and \(p = 0.33\). Suppose we want to determine the probability \(P(2 < S_{10} \le 8)\). Let \(A_k = \{\omega: S_{10} (\omega) = k\}\), which we usually shorten to \(A_k = \{S_{10} = k\}\). Now the \(A_k\) form a partition, since we cannot have \(\omega \in A_k\) and \(\omega \in A_k\) \(j \ne k\) (i.e., for any \(\omega\), we cannot have two values for \(S_n (\omega)\)). Now,
\(\{2 < S_{10} \le 8\} = A_3 \bigvee A_4 \bigvee A_5 \bigvee A_6 \bigvee A_7 \bigvee A_8\)
since \(S_{10}\) takes on a value greater than 2 but no greater than 8 iff it takes one of the integer values from 3 to 8. By the additivity of probability,
Mass transfer and induced probability distribution
Because of the abstract nature of the basic space and the class of events, we are limited in the kinds of calculations that can be performed meaningfully with the probabilities on the basic space. We represent probability as mass distributed on the basic space and visualize this with the aid of general Venn diagrams and minterm maps. We now think of the mapping from \(\Omega\) to R as a producing a point-by-point transfer of the probability mass to the real line. This may be done as follows:
To any set \(M\) on the real line assign probability mass \(P_X(M) = P(X^{-1}(M))\)
It is apparent that \(P_X(M) \ge 0\) and \(P_X\)(R) \(= P(\Omega) = 1\). And because of the preservation of set operations by the inverse mapping
\(P_X(\bigvee_{i = 1}^{\infty} M_i) = P(X^{-1}(\bigvee_{i = 1}^{\infty} M_i)) = P(\bigvee_{i = 1}^{\infty} X^{-1}(M_i)) = \sum_{i = 1}^{\infty} P(X^{-1}(M_i)) = \sum_{i = 1}^{\infty} P_X(M_i)\)
This means that \(P_X\) has the properties of a probability measure defined on the subsets of the real line. Some results of measure theory show that this probability is defined uniquely on a class of subsets of R that includes any set normally encountered in applications. We have achieved a point-by-point transfer of the probability apparatus to the real line in such a manner that we can make calculations about the random variable \(X\). We call \(P_X\) the probability measure induced by X. Its importance lies in the fact that \(P(X \in M) = P_X(M)\). Thus, to determine the likelihood that random quantity X will take on a value in set M, we determine how much induced probability mass is in the set M. This transfer produces what is called the probability distribution for X. In the chapter "Distribution and Density Functions", we consider useful ways to describe the probability distribution induced by a random variable. We turn first to a special class of random variables.
Simple random variables
We consider, in some detail, random variables which have only a finite set of possible values. These are called simple random variables. Thus the term “simple” is used in a special, technical sense. The importance of simple random variables rests on two facts. For one thing, in practice we can distinguish only a finite set of possible values for any random variable. In addition, any random variable may be approximated as closely as pleased by a simple random variable. When the structure and properties of simple random variables have been examined, we turn to more general cases. Many properties of simple random variables extend to the general case via the approximation procedure.
Representation with the aid of indicator functions
In order to deal with simple random variables clearly and precisely, we must find suitable ways to express them analytically. We do this with the aid of indicator functions. Three basic forms of representation are encountered. These are not mutually exclusive representatons.
Standard or canonical form, which displays the possible values and the corresponding events. If X takes on distinct values
\(\{t_1, t_2, \cdot\cdot\cdot, t_n\}\) with respective probabilities \(\{p_1, p_2, \cdot\cdot\cdot, p_n\}\)
and if \(A_i = \{X = t_i\}\), for \(1 \le i \le n\), then \(\{A_1, A_2, \cdot \cdot\cdot, A_n\}\) is a partition (i.e., on any trial, exactly one of these events occurs). We call this the partition determined by (or, generated by) X. We may write
If \(X(\omega) = t_i\), then \(\omega \in A_i\), so that \(I_{A_i} (\omega) = 1\) and all the other indicator functions have value zero. The summation expression thus picks out the correct value \(t_i\). This is true for any \(t_i\), so the expression represents \(X(\omega)\)for all \(\omega\). The distinct set \(\{A, B, C\}\) of the values and the corresponding probabilities \(\{p_1, p_2, \cdot\cdot\cdot, p_n\}\) constitute the distribution for X. Probability calculations for X are made in terms of its distribution. One of the advantages of the canonical form is that it displays the range (set of values), and if the probabilities \(\{A, B, C, D\}\) are known, the distribution is determined. Note that in canonical form, if one of the \(t_i\) has value zero, we include that term. For some probability distributions it may be that \(P(A_i) = 0\) for one or more of the \(t_i\). In that case, we call these values null values, for they can only occur with probability zero, and hence are practically impossible. In the general formulation, we include possible null values, since they do not affect any probabilitiy calculations.
Example \(\PageIndex{3}\) Successes in Bernoulli trials
As the analysis of Bernoulli trials and the binomial distribution shows (see Section 4.8), canonical form must be
\(S_n = \sum_{k = 0}^{n} k I_{A_k}\) with \(P(A_k) = C(n, k) p^{k} (1-p)^{n - k}\), \(0 \le k \le n\)
For many purposes, both theoretical and practical, canonical form is desirable. For one thing, it displays directly the range (i.e., set of values) of the random variable. The distribution consists of the set of values \(\{t_k: 1 \le k \le n\}\) paired with the corresponding set of probabilities \(\{p_k: 1 \le k \le n\}\), where \(p_k = P(A_k) = P(X = t_k)\).
Simple random variable X may be represented by a primitive form
Remarks
- If \(\{C_j: 1 \le j \le m\}\) is a disjoint class, but \(\bigcup_{j = 1}^{m} C_j \ne \Omega\), we may append the event \(C_{m + 1} = [\bigcup_{j = 1}^{m} C_j]^c\) and assign value zero to it.
- We say a primitive form, since the representation is not unique. Any of the Ci may be partitioned, with the same value \(c_i\) associated with each subset formed.
- Canonical form is a special primitive form. Canonical form is unique, and in many ways normative.
Example \(\PageIndex{4}\) Simple random variables in primitive form
- A wheel is spun yielding, on a equally likely basis, the integers 1 through 10. Let \(C_i\) be the event the wheel stops at \(i\), \(1 \le i \le 10\). Each \(P(C_i) = 0.1\). If the numbers 1, 4, or 7 turn up, the player loses ten dollars; if the numbers 2, 5, or 8 turn up, the player gains nothing; if the numbers 3, 6, or 9 turn up, the player gains ten dollars; if the number 10 turns up, the player loses one dollar. The random variable expressing the results may be expressed in primitive form as
\(X = -10 I_{C_1} + 0 I_{C_2} + 10 I_{C_3} - 10 I_{C_4} + 0 I_{C_5} + 10 I_{C_6} - 10 I_{C_7} + 0 I_{C_8} + 10I_{C_9} - I_{C_{10}}\)
-
A store has eight items for sale. The prices are $3.50, $5.00, $3.50, $7.50, $5.00, $5.00, $3.50, and $7.50, respectively. A customer comes in. She purchases one of the items with probabilities 0.10, 0.15, 0.15, 0.20, 0.10 0.05, 0.10 0.15. The random variable expressing the amount of her purchase may be written
\(X = 3.5 I_{C_1} + 5.0 I_{C_2} + 3.5 I_{C_3} + 7.5 I_{C_4} + 5.0 I_{C_5} + 5.0 I_{C_6} + 3.5 I_{C_7} + 7.5 I_{C_8}\)
We commonly have X represented in affine form, in which the random variable is represented as an affine combination of indicator functions (i.e., a linear combination of the indicator functions plus a constant, which may be zero).
In this form, the class \(\{E_1, E_2, \cdot\cdot\cdot, E_m\}\) is not necessarily mutually exclusive, and the coefficients do not display directly the set of possible values. In fact, the \(E_i\) often form an independent class. Remark. Any primitive form is a special affine form in which \(c_0 = 0\) and the \(E_i\) form a partition.
Example \(\PageIndex{5}\)
Consider, again, the random variable \(S_n\) which counts the number of successes in a sequence of \(n\) Bernoulli trials. If \(E_i\) is the event of a success on the \(i\)th trial, then one natural way to express the count is
\(S_n = \sum_{i = 1}^{n} I_{E_i}\), with \(P(E_i) = p\) \(1 \le i \le n\)
This is affine form, with \(c_0 = 0\) and \(c_i =1\) for \(1 \le i \le n\). In this case, the \(E_i\) cannot form a mutually exclusive class, since they form an independent class.
Events generated by a simple random variable: canonical form
We may characterize the class of all inverse images formed by a simple random \(X\) in terms of the partition it determines. Consider any set \(M\) of real numbers. If \(t_i\) in the range of \(X\) is in \(M\), then every point \(\omega \in A_i\) maps into \(t_i\), hence into \(M\). If the set \(J\) is the set of indices \(i\) such that \(t_i \in M\), then
Only those points \(\omega\) in \(A_M = \bigvee_{i \in J} A_i\) map into \(M\).
Hence, the class of events (i.e., inverse images) determined by \(X\) consists of the impossible event \(\emptyset\), the sure event \(\Omega\), and the union of any subclass of the \(A_i\) in the partition determined by \(X\).
Example \(\PageIndex{6}\) Events determined by a simple random variable
Suppose simple random variable \(X\) is represented in canonical form by
\(X = -2I_A - I_B + 0 I_C + 3I_D\)
Then the class \(\{A, B, C, D\}\) is the partition determined by \(X\) and the range of \(X\) is \(\{-2, -1, 0, 3\}\).
- If \(M\) is the interval [-2, 1], the the values -2, -1, and 0 are in \(M\) and \(X^{-1}(M) = A \bigvee B \bigvee C\).
- If \(M\) is the set (-2, -1] \(\cup\) [1, 5], then the values -1, 3 are in \(M\) and \(X^{-1}(M) = B \bigvee D\).
- The event \(\{X \le 1\} = \{X \in (-\infty, 1]\} = X^{-1} (M)\), where \(M = (- \infty, 1]\). Since values -2, -1, 0 are in \(M\), the event \(\{X \le 1\} = A \bigvee B \bigvee C\).
Determination of the distribution
Determining the partition generated by a simple random variable amounts to determining the canonical form. The distribution is then completed by determining the probabilities of each event \(A_k = \{X = t_k\}\).
From a primitive form
Before writing down the general pattern, we consider an illustrative example.
Example \(\PageIndex{7}\) The distribution from a primitive form
Suppose one item is selected at random from a group of ten items. The values (in dollars) and respective probabilities are
| \(c_j\) | 2.00 | 1.50 | 2.00 | 2.50 | 1.50 | 1.50 | 1.00 | 2.50 | 2.00 | 1.50 |
| \(P(C_j)\) | 0.08 | 0.11 | 0.07 | 0.15 | 0.10 | 0.09 | 0.14 | 0.08 | 0.08 | 0.10 |
By inspection, we find four distinct values: \(t _ 1 = 1.00\), \(t_2 = 1.50\), \(t_3 = 2.00\), and \(t_4 = 2.50\). The value 1.00 is taken on for \(\omega \in C_7\), so that \(A_1 = C_7\) and \(P(A_1) = P(C_7) = 0.14\). Value 1.50 is taken on for \(\omega \in C_2, C_5, C_6, C_{10}\) so that
\(A_2 = C_2 \bigvee C_5 \bigvee C_6 \bigvee C_{10}\) and \(P(A_2) = P(C_2) + P(C_5) + P(C_6) + P(C_{10}) = 0.40\)
Similarly
\(P(A_3) = P(C_1) + P(C_3) + P(C_9) = 0.23\) and \(P(A_4) = P(C_4) + P(C_8) = 0.25\)
The distribution for X is thus
| \(k\) | 1.00 | 1.50 | 2.00 | 2.50 |
| \(P(X = k)\) | 0.14 | 0.40 | 0.23 | 0.23 |
The general procedure may be formulated as follows:
If \(X = \sum_{j = 1}^{m} c_j I_{c_j}\), we identify the set of distinct values in the set \(\{c_j: 1 \le j \le m\}\). Suppose these are \(t_1 < t_2 < \cdot\cdot\cdot < t_n\). For any possible value \(t_i\) in the range, identify the index set \(J_i\) of those \(j\) such that \(c_j = t_i\) Then the terms
\(\sum_{J_i} c_j I_{c_j} = t_i \sum_{J_i} I_{c_j} = t_i I_{A_i}\), where \(A_i = \bigvee_j \in J_i C_j\),
and
\(P(A_i) = P(X = t_i) = \sum_{j \in J} P(C_j)\)
Examination of this procedure shows that there are two phases:
- Select and sort the distinct values \(t_1, t_2, \cdot\cdot\cdot, t_n\)
- Add all probabilities associated with each value \(t_i\) to determine \(P(X = t_i)\)
We use the m-function csort which performs these two operations (see Example 4 from "Minterms and MATLAB Calculations").
Example \(\PageIndex{8}\) Use of csort on Example 6.1.7
>> C = [2.00 1.50 2.00 2.50 1.50 1.50 1.00 2.50 2.00 1.50]; % Matrix of c_j
>> pc = [0.08 0.11 0.07 0.15 0.10 0.09 0.14 0.08 0.08 0.10]; % Matrix of P(C_j)
>> [X,PX] = csort(C,pc); % The sorting and consolidating operation
>> disp([X;PX]') % Display of results
1.0000 0.1400
1.5000 0.4000
2.0000 0.2300
2.5000 0.2300
For a problem this small, use of a tool such as csort is not really needed. But in many problems with large sets of data the m-function csort is very useful.
From affine form
Suppose \(X\) is in affine form,
\(X = c_0 + c_1 I_{E_1} + c_2 I_{E_2} + \cdot\cdot\cdot + c_m I_{E_m} = c_0 + \sum_{j = 1}^{m} c_j I_{E_j}\)
We determine a particular primitive form by determining the value of \(X\) on each minterm generated by the class \(\{E_j: 1 \le j \le m\}\). We do this in a systematic way by utilizing minterm vectors and properties of indicator functions.
\(X\) is constant on each minterm generated by the class \(\{E_1, E_2, \cdot\cdot\cdot, E_m\}\) since, as noted in the treatment of the minterm expansion, each indicator function \(I_{E_i}\) is constant on each minterm. We determine the value \(s_i\) of \(X\) on each minterm \(M_i\). This describes \(X\) in a special primitive form
We apply the csort operation to the matrices of values and minterm probabilities to determine the distribution for \(X\).
We illustrate with a simple example. Extension to the general case should be quite evident. First, we do the problem “by hand” in tabular form. Then we use the m-procedures to carry out the desired operations.
Example \(\PageIndex{9}\) Finding the distribution from affine form
A mail order house is featuring three items (limit one of each kind per customer). Let
- \(E_1\) = the event the customer orders item 1, at a price of 10 dollars.
- \(E_2\) = the event the customer orders item 2, at a price of 18 dollars.
- \(E_3\) = the event the customer orders item 3, at a price of 10 dollars.
There is a mailing charge of 3 dollars per order.
We suppose \(\{E_1, E_2, E_3\}\) is independent with probabilities 0.6, 0.3, 0.5, respectively. Let \(X\) be the amount a customer who orders the special items spends on them plus mailing cost. Then, in affine form,
\(X = 10 I_{E_1} + 18 I_{E_2} + 10 I_{E_3} + 3\)
We seek first the primitive form, using the minterm probabilities, which may calculated in this case by using the m-function minprob.
- To obtain the value of \(X\) on each minterm we
- Multiply the minterm vector for each generating event by the coefficient for that event
- Sum the values on each minterm and add the constant
To complete the table, list the corresponding minterm probabilities.
\(i\) 10 \(I_{E_1}\) 18 \(I_{E_2}\) 10 \(I_{E_3}\) c \(s-i\) \(pm_i\) 0 0 0 0 3 3 0.14 1 0 0 10 3 13 0.14 2 0 18 0 3 21 0.06 3 0 18 10 3 31 0.06 4 10 0 0 3 13 0.21 5 10 0 10 3 23 0.21 6 10 18 0 3 31 0.09 7 10 18 10 3 41 0.09 We then sort on the \(s_i\), the values on the various \(M_i\), to expose more clearly the primitive form for \(X\).
“Primitive form” Values \(i\) \(s_i\) \(pm_i\) 0 3 0.14 1 13 0.14 4 13 0.21 2 21 0.06 5 23 0.21 3 31 0.06 6 31 0.09 7 41 0.09 The primitive form of \(X\) is thus
\(X = 3I_{M_0} + 12I_{M_1} + 13I_{M_4} + 21I_{M_2} + 23I_{M_5} + 31I_{M_3} + 31I_{M_6} + 41I_{M_7}
We note that the value 13 is taken on on minterms \(M_1\) and \(M_4\). The probability \(X\) has the value 13 is thus \(p(1) + p(4)\). Similarly, \(X\) has value 31 on minterms \(M_3\) and \(M_6\).
- To complete the process of determining the distribution, we list the sorted values and consolidate by adding together the probabilities of the minterms on which each value is taken, as follows:
\(k\) \(t_k\) \(p_k\) 1 3 0.14 2 13 0.14 + 0.21 = 0.35 3 21 0.06 4 23 0.21 5 31 0.06 + 0.09 = 0.15 6 41 0.09 The results may be put in a matrix \(X\) of possible values and a corresponding matrix PX of probabilities that \(X\) takes on each of these values. Examination of the table shows that
\(X =\) [3 13 21 23 31 41] and \(PX =\) [0.14 0.35 0.06 0.21 0.15 0.09]
Matrices \(X\) and PX describe the distribution for \(X\).
An m-procedure for determining the distribution from affine form
We now consider suitable MATLAB steps in determining the distribution from affine form, then incorporate these in the m-procedure canonic for carrying out the transformation. We start with the random variable in affine form, and suppose we have available, or can calculate, the minterm probabilities.
The procedure uses mintable to set the basic minterm vector patterns, then uses a matrix of coefficients, including the constant term (set to zero if absent), to obtain the values on each minterm. The minterm probabilities are included in a row matrix.
Having obtained the values on each minterm, the procedure performs the desired consolidation by using the m-function csort.
Example \(\PageIndex{10}\) Steps in determining the distribution for X in Example 6.1.9
>> c = [10 18 10 3]; % Constant term is listed last
>> pm = minprob(0.1*[6 3 5]);
>> M = mintable(3) % Minterm vector pattern
M =
0 0 0 0 1 1 1 1
0 0 1 1 0 0 1 1
0 1 0 1 0 1 0 1
% - - - - - - - - - - - - - - % An approach mimicking ``hand'' calculation
>> C = colcopy(c(1:3),8) % Coefficients in position
C =
10 10 10 10 10 10 10 10
18 18 18 18 18 18 18 18
10 10 10 10 10 10 10 10
>> CM = C.*M % Minterm vector values
CM =
0 0 0 0 10 10 10 10
0 0 18 18 0 0 18 18
0 10 0 10 0 10 0 10
>> cM = sum(CM) + c(4) % Values on minterms
cM =
3 13 21 31 13 23 31 41
% - - - - - - - - - - - - - % Practical MATLAB procedure
>> s = c(1:3)*M + c(4)
s =
3 13 21 31 13 23 31 41
>> pm = 0.14 0.14 0.06 0.06 0.21 0.21 0.09 0.09 % Extra zeros deleted
>> const = c(4)*ones(1,8);}
>> disp([CM;const;s;pm]') % Display of primitive form
0 0 0 3 3 0.14 % MATLAB gives four decimals
0 0 10 3 13 0.14
0 18 0 3 21 0.06
0 18 10 3 31 0.06
10 0 0 3 13 0.21
10 0 10 3 23 0.21
10 18 0 3 31 0.09
10 18 10 3 41 0.09
>> [X,PX] = csort(s,pm); % Sorting on s, consolidation of pm
>> disp([X;PX]') % Display of final result
3 0.14
13 0.35
21 0.06
23 0.21
31 0.15
41 0.09
The two basic steps are combined in the m-procedure canonic, which we use to solve the previous problem.
Example \(\PageIndex{11}\) Use of canonic on the variables of Example 6.1.10
>> c = [10 18 10 3]; % Note that the constant term 3 must be included last
>> pm = minprob([0.6 0.3 0.5]);
>> canonic
Enter row vector of coefficients c
Enter row vector of minterm probabilities pm
Use row matrices X and PX for calculations
Call for XDBN to view the distribution
>> disp(XDBN)
3.0000 0.1400
13.0000 0.3500
21.0000 0.0600
23.0000 0.2100
31.0000 0.1500
41.0000 0.0900
With the distribution available in the matrices \(X\) (set of values) and PX (set of probabilities), we may calculate a wide variety of quantities associated with the random variable.
We use two key devices:
- Use relational and logical operations on the matrix of values \(X\) to determine a matrix \(M\) which has ones for those values which meet a prescribed condition. \(P(X \in M)\): PM = M*PX'
- Determine \(G = g(X) = [g(X_1) g(X_2) \cdot\cdot\cdot g(X_n)]\) by using array operations on matrix \(X\). We have two alternatives:
- Use the matrix \(G\), which has values \(g(t_i)\) for each possible value \(t_i\) for \(X\), or,
- Apply csort to the pair \((G, PX)\) to get the distribution for \(Z = g(X)\). This distribution (in value and probability matrices) may be used in exactly the same manner as that for the original random variable \(X\).
Example \(\PageIndex{12}\) Continuation of Example 6.1.11
Suppose for the random variable \(X\) in Example 6.11 it is desired to determine the probabilities
\(P(15 \le X \le 35)\), \(P(|X - 20| \le 7)\), and \((X - 10) (X - 25) > 0)\)
>> M = (X>=15)&(X<=35); M = 0 0 1 1 1 0 % Ones for minterms on which 15 <= X <= 35 >> PM = M*PX' % Picks out and sums those minterm probs PM = 0.4200 >> N = abs(X-20)<=7; N = 0 1 1 1 0 0 % Ones for minterms on which |X - 20| <= 7 >> PN = N*PX' % Picks out and sums those minterm probs PN = 0.6200 >> G = (X - 10).*(X - 25) G = 154 -36 -44 -26 126 496 % Value of g(t_i) for each possible value >> P1 = (G>0)*PX' % Total probability for those t_i such that P1 = 0.3800 % g(t_i) > 0 >> [Z,PZ] = csort(G,PX) % Distribution for Z = g(X) Z = -44 -36 -26 126 154 496 PZ = 0.0600 0.3500 0.2100 0.1500 0.1400 0.0900 >> P2 = (Z>0)*PZ' % Calculation using distribution for Z P2 = 0.3800
Example \(\PageIndex{13}\) Alternate formulation of Example 4.3.3 from "Composite Trials"
Ten race cars are involved in time trials to determine pole positions for an upcoming race. To qualify, they must post an average speed of 125 mph or more on a trial run. Let \(E_i\) be the event the \(i\)th car makes qualifying speed. It seems reasonable to suppose the class \(\{E_i: 1 \le i \le 10\}\) is independent. If the respective probabilities for success are 0.90, 0.88, 0.93, 0.77, 0.85, 0.96, 0.72, 0.83, 0.91, 0.84, what is the probability that \(k\) or more will qualify (\(k\) = 6,7,8,9,10)?
Solution
Let \(X = \sum_{i = 1}^{10} I_{E_i}\)
>> c = [ones(1,10) 0];
>> P = [0.90, 0.88, 0.93, 0.77, 0.85, 0.96, 0.72, 0.83, 0.91, 0.84];
>> canonic
Enter row vector of coefficients c
Enter row vector of minterm probabilities minprob(P)
Use row matrices X and PX for calculations
Call for XDBN to view the distribution
>> k = 6:10;
>> for i = 1:length(k)
Pk(i) = (X>=k(i))*PX';
end
>> disp(Pk)
0.9938 0.9628 0.8472 0.5756 0.2114
This solution is not as convenient to write out. However, with the distribution for \(X\) as defined, a great many other probabilities can be determined. This is particularly the case when it is desired to compare the results of two independent races or “heats.” We consider such problems in the study of Independent Classes of Random Variables.
A function form for canonic
One disadvantage of the procedure canonic is that it always names the output \(X\) and PX. While these can easily be renamed, frequently it is desirable to use some other name for the random variable from the start. A function form, which we call canonicf, is useful in this case.
Example \(\PageIndex{14}\) Alternate solution of Example 6.1.13, using canonicf
>> c = [10 18 10 3];
>> pm = minprob(0.1*[6 3 5]);
>> [Z,PZ] = canonicf(c,pm);
>> disp([Z;PZ]') % Numbers as before, but the distribution
3.0000 0.1400 % matrices are now named Z and PZ
13.0000 0.3500
21.0000 0.0600
23.0000 0.2100
31.0000 0.1500
41.0000 0.0900
General random variables
The distribution for a simple random variable is easily visualized as point mass concentrations at the various values in the range, and the class of events determined by a simple random variable is described in terms of the partition generated by \(X\) (i.e., the class of those events of the form \(A_i = [X = t_i]\) for each \(t_i\) in the range). The situation is conceptually the same for the general case, but the details are more complicated. If the random variable takes on a continuum of values, then the probability mass distribution may be spread smoothly on the line. Or, the distribution may be a mixture of point mass concentrations and smooth distributions on some intervals. The class of events determined by \(X\) is the set of all inverse images \(X^{-1} (M)\) for \(M\) any member of a general class of subsets of subsets of the real line known in the mathematical literature as the Borel sets. There are technical mathematical reasons for not saying M is any subset, but the class of Borel sets is general enough to include any set likely to be encountered in applications—certainly at the level of this treatment. The Borel sets include any interval and any set that can be formed by complements, countable unions, and countable intersections of Borel sets. This is a type of class known as a sigma algebra of events. Because of the preservation of set operations by the inverse image, the class of events determined by random variable \(X\) is also a sigma algebra, and is often designated \(\sigma(X)\). There are some technical questions concerning the probability measure \(P_X\) induced by \(X\), hence the distribution. These also are settled in such a manner that there is no need for concern at this level of analysis. However, some of these questions become important in dealing with random processes and other advanced notions increasingly used in applications. Two facts provide the freedom we need to proceed with little concern for the technical details.
\(X^{-1} (M)\) is an event for every Borel set \(M\) iff for every semi-infinite interval \((-\infty, t]\) on the real line \(X^{-1} ((-\infty, t])\) is an event.
The induced probability distribution is determined uniquely by its assignment to all intervals of the form \((-\infty, t]\).
These facts point to the importance of the distribution function introduced in the next chapter.
Another fact, alluded to above and discussed in some detail in the next chapter, is that any general random variable can be approximated as closely as pleased by a simple random variable. We turn in the next chapter to a description of certain commonly encountered probability distributions and ways to describe them analytically.


