1.3: Interpretations

What is Probability?

The formal probability system is a model whose usefulness can only be established by examining its structure and determining whether patterns of uncertainty and likelihood in any practical situation can be represented adequately. With the exception of the sure event and the impossible event, the model does not tell us how to assign probability to any given event. The formal system is consistent with many probability assignments, just as the notion of mass is consistent with many different mass assignments to sets in the basic space.

The defining properties (P1), (P2), (P3) and derived properties provide consistency rules for making probability assignments. One cannot assign negative probabilities or probabilities greater than one. The sure event is assigned probability one. If two or more events are mutually exclusive, the total probability assigned to the union must equal the sum of the probabilities of the separate events. Any assignment of probability consistent with these conditions is allowed.

One may not know the probability assignment to every event. Just as the defining conditions put constraints on allowable probability assignments, they also provide important structure. A typical applied problem provides the probabilities of members of a class of events (perhaps only a few) from which to determine the probabilities of other events of interest. We consider an important class of such problems in the next chapter.

There is a variety of points of view as to how probability should be interpreted. These impact the manner in which probabilities are assigned (or assumed). One important dichotomy among practitioners.

• One group believes probability is objective in the sense that it is something inherent in the nature of things. It is to be discovered, if possible, by analysis and experiment. Whether we can determine it or not, “it is there.”
• Another group insists that probability is a condition of the mind of the person making the probability assessment. From this point of view, the laws of probability simply impose rational consistency upon the way one assigns probabilities to events. Various attempts have been made to find objective ways to measure the strength of one's belief or degree of certainty that an event will occur. The probability \(P(A)\) expresses the degree of certainty one feels that event A will occur. One approach to characterizing an individual's degree of certainty is to equate his assessment of \(P(A)\) with the amount a he is willing to pay to play a game which returns one unit of money if A occurs, for a gain of \((1 - a)\), and returns zero if A does not occur, for a gain of \(-a\). Behind this formulation is the notion of a fair game, in which the “expected” or “average” gain is zero.

The early work on probability began with a study of relative frequencies of occurrence of an event under repeated but independent trials. This idea is so imbedded in much intuitive thought about probability that some probabilists have insisted that it must be built into the definition of probability. This approach has not been entirely successful mathematically and has not attracted much of a following among either theoretical or applied probabilists. In the model we adopt, there is a fundamental limit theorem, known as Borel's theorem, which may be interpreted “if a trial is performed a large number of times in an independent manner, the fraction of times that event \(A\) occurs approaches as a limit the value \(P(A)\). Establishing this result (which we do not do in this treatment) provides a formal validation of the intuitive notion that lay behind the early attempts to formulate probabilities. Inveterate gamblers had noted long-run statistical regularities, and sought explanations from their mathematically gifted friends. From this point of view, probability is meaningful only in repeatable situations. Those who hold this view usually assume an objective view of probability. It is a number determined by the nature of reality, to be discovered by repeated experiment.

There are many applications of probability in which the relative frequency point of view is not feasible. Examples include predictions of the weather, the outcome of a game or a horse race, the performance of an individual on a particular job, the success of a newly designed computer. These are unique, nonrepeatable trials. As the popular expression has it, “You only go around once.” Sometimes, probabilities in these situations may be quite subjective. As a matter of fact, those who take a subjective view tend to think in terms of such problems, whereas those who take an objective view usually emphasize the frequency interpretation.

Subjective probability and a football game

The probability that one's favorite football team will win the next Superbowl Game may well be only a subjective probability of the bettor. This is certainly not a probability that can be determined by a large number of repeated trials. The game is only played once. However, the subjective assessment of probabilities may be based on intimate knowledge of relative strengths and weaknesses of the teams involved, as well as factors such as weather, injuries, and experience. There may be a considerable objective basis for the subjective assignment of probability. In fact, there is often a hidden “frequentist” element in the subjective evaluation. There is an assessment (perhaps unrealized) that in similar situations the frequencies tend to coincide with the value subjectively assigned.

The probabilty of rain

Newscasts often report that the probability of rain of is 20 percent or 60 percent or some other figure. There are several difficulties here.

• To use the formal mathematical model, there must be precision in determining an event. An event either occurs or it does not. How do we determine whether it has rained or not? Must there be a measurable amount? Where must this rain fall to be counted? During what time period? Even if there is agreement on the area, the amount, and the time period, there remains ambiguity: one cannot say with logical certainty the event did occur or it did not occur. Nevertheless, in this and other similar situations, use of the concept of an event may be helpful even if the description is not definitive. There is usually enough practical agreement for the concept to be useful.
• What does a 30 percent probability of rain mean? Does it mean that if the prediction is correct, 30 percent of the area indicated will get rain (in an agreed amount) during the specified time period? Or does it mean that 30 percent of the occasions on which such a prediction is made there will be significant rainfall in the area during the specified time period? Again, the latter alternative may well hide a frequency interpretation. Does the statement mean that it rains 30 percent of the times when conditions are similar to current conditions?

Regardless of the interpretation, there is some ambiguity about the event and whether it has occurred. And there is some difficulty with knowing how to interpret the probability figure. While the precise meaning of a 30 percent probability of rain may be difficult to determine, it is generally useful to know whether the conditions lead to a 20 percent or a 30 percent or a 40 percent probability assignment. And there is no doubt that as weather forecasting technology and methodology continue to improve the weather probability assessments will become increasingly useful.

Another common type of probability situation involves determining the distribution of some characteristic over a population—usually by a survey. These data are used to answer the question: What is the probability (likelihood) that a member of the population, chosen “at random” (i.e., on an equally likely basis) will have a certain characteristic?

Empirical probability based on survey data

A survey asks two questions of 300 students: Do you live on campus? Are you satisfied with the recreational facilities in the student center? Answers to the latter question were categorized “reasonably satisfied,” “unsatisfied,” or “no definite opinion.” Let \(C\) be the event “on campus;” \(O\) be the event “off campus;” \(S\) be the event “reasonably satisfied;” \(U\) be the event ”unsatisfied;” and \(N\) be the event “no definite opinion.” Data are shown in the following table.

Survey Data

	S	U	N
C	127	31	42
O	46	43	11

If an individual is selected on an equally likely basis from this group of 300, the probability of any of the events is taken to be the relative frequency of respondents in each category corresponding to an event. There are 200 on campus members in the population, so \(P(C) = 200/300\) and \(P(O) = 100/300\). The probability that a student selected is on campus and satisfied is taken to be \(P(CS) = 127/300\). The probability a student is either on campus and satisfied or off campus and not satisfied is

\(P(CS \bigvee OU) = P(CS) + P(OU) = 127/300 + 43/300 = 170/300\)

If there is reason to believe that the population sampled is representative of the entire student body, then the same probabilities would be applied to any student selected at random from the entire student body.

It is fortunate that we do not have to declare a single position to be the “correct” viewpoint and interpretation. The formal model is consistent with any of the views set forth. We are free in any situation to make the interpretation most meaningful and natural to the problem at hand. It is not necessary to fit all problems into one conceptual mold; nor is it necessary to change mathematical model each time a different point of view seems appropriate.

Probability and odds

Often we find it convenient to work with a ratio of probabilities. If \(A\) and \(B\) are events with positive probability the odds favoring \(A\) over \(B\) is the probability ratio \(P(A)P(B)\). If not otherwise specified, \(B\) is taken to be \(A^c\) and we speak of the odds favoring \(A\)

\(O(A) = \dfrac{P(A)}{P(A^c)} = \dfrac{P(A)}{1 - P(A)}\)

This expression may be solved algebraically to determine the probability from the odds

\(P(A) = \dfrac{O(A)}{1 + O(A)}\)

In particular, if \(O(A) = a/b\) then \(P(A) = \dfrac{a/b}{1+a/b} = \dfrac{a}{a+b}\).

\(O(A) = 0.7/0.3 = 7/3\). If the odds favoring \(A\) is 5/3, then \(P(A) = 5/(5 + 3) = 5/8\).

Partitions and Boolean combinations of events

The countable additivity property (P3) places a premium on appropriate partitioning of events.

Definition

A partition is a mutually exclusive class

\({A_i : i \in J}\) such that \(\Omega = \bigvee_{i \in J} A_i\)

A partition of event \(A\) is a mutually exclusive class

\({A_i : i \in J}\) such that \(A = \bigvee_{i \in J} A_i\)

Remarks.

• A partition is a mutually exclusive class of events such that one (and only one) must occur on each trial.
• A partition of event \(A\) is a mutually exclusive class of events such that \(A\) occurs iff one (and only one) of the \(A_i\) occurs.
• A partition (no qualifier) is taken to be a partition of the sure event \(\Omega\).
• If class \({B_i : i \in J}\) is mutually exclusive and \(A \subset B = \bigvee_{i \in J} B_i\), then the class \({AB_i : i \in J}\) is a partition of \(A\) and \(A = \bigvee_{i \in J} AB_i\).

We may begin with a sequence \({A_1: 1 \le i}\) and determine a mutually exclusive (disjoint) sequence \({B_1: 1 \le i}\) as follows:

\(B_1 = A_1\), and for any \(i > 1\), \(B_i = A_i A_{1}^{c} A_{2}^{c} \cdot\cdot\cdot A_{i - 1}^{c}\)

Thus each \(B_i\) is the set of those elements of \(A_i\) not in any of the previous members of the sequence.

This representation is used to show that subadditivity (P9) follows from countable additivity and property (P6). Since each \(B_i \subset A_i\), by (P6) \(P(B_i) \le P(A_i)\). Now

\(P(\bigcup_{i = 1}^{\infty} A_i) = P(\bigvee_{i = 1}^{\infty} B_i) = \sum_{i = 1}^{\infty} P(B_i) \le \sum_{i = 1}^{\infty} P(A_i)\)

The representation of a union as a disjoint union points to an important strategy in the solution of probability problems. If an event can be expressed as a countable disjoint union of events, each of whose probabilities is known, then the probability of the combination is the sum of the individual probailities. In in the module on Partitions and Minterms, we show that any Boolean combination of a finiteclass of events can be expressed as a disjoint union in a manner that often facilitates systematic determination of the probabilities.

The indicator function

One of the most useful tools for dealing with set combinations (and hence with event combinations) is the indicator function \(I_E\) for a set \(E \subset \Omega\). It is defined very simply as follows:

\(I_E (\omega) = \begin{cases}1 & \text{for } \omega \in E \\ 0 & \text{for } \omega \in E^c \end{cases}\)

Remark. Indicator fuctions may be defined on any domain. We have occasion in various cases to define them on the real line and on higher dimensional Euclidean spaces. For example, if \(M\) is the interval [\(a,b\)] on the real line then \(I_M(t) = 1\) for each \(t\) in the interval (and is zero otherwise). Thus we have a step function with unit value over the interval \(M\). In the abstract basic space \(\Omega\) we cannot draw a graph so easily. However, with the representation of sets on a Venn diagram, we can give a schematic representation, as in Figure 1.3.1.

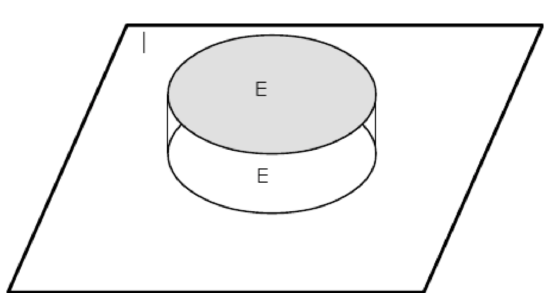
Figure 1.3.1. Representation of the indicator function \(I_E\) for event \(E\).

Much of the usefulness of the indicator function comes from the following properties.

(IF1): \(I_A \le I_B\) iff \(A \subset B\). If \(I_A \le I_B\), then \(\omega \in A\) implies \(I_A (\omega) = I_B (\omega) = 1\), so \(\omega \in B\), then \(I_A (\omega) = 1\) implies \(\omega \in A\) implies \(\omega \in B\) implies \(I_B (\omega) = 1\).
(IF2): \(I_A = I_B\) iff \(A = B\)

\(A = B\) iff both \(A \subset B\) and \(B \subset A\) iff \(I_A \le I_B\) and \(I_B \le I_A\) iff \(I_A = I_B\)

(IF3): \(I_{A^c} = 1 - I_A\) This follows from the fact \(I_{A^c} (\omega) = 1\) iff \(I_A (\omega) = 0\).
(IF4): \(I_{AB} = I_A I_B = \text{min } {I_A, I_B}\) (extends to any class) An element ω belongs to the intersection iff it belongs to all iff the indicator function for each event is one iff the product of the indicator functions is one.
(IF5): \(I_{A \cup B} = I_A + I_B - I_A I_B = \text{min }{I_A, I_B}\) (the maximum rule extends to any class) The maximum rule follows from the fact that \(\omega\) is in the union iff it is in any one or more of the events in the union iff any one or more of the individual indicator function has value one iff the maximum is one. The sum rule for two events is established by DeMorgan's rule and properties (IF2), (IF3), and (IF4).

\(I_{A \cup B} = 1 - I_{A^c B^c} = 1 - [1 - I_A][1 - I_B] = 1 - 1 + I_B + I_A - I_A I_B\)

(IF6): If the pair \({A, B}\) is disjoint, \(I_{A \bigvee B} = I_A+ I_B\) (extends to any disjoint class)

The following example illustrates the use of indicator functions in establishing relationships between set combinations. Other uses and techniques are established in the module on Partitions and Minterms.

Indicator functions and set combinations

Suppose \({A_i : 1 \le i \le n}\) is a partition.

If \(B = \bigvee_{i = 1}^{n} A_i C_i\), then \(B^c = \bigvee_{i = 1}^{n} A_i C_{i}^{c}\)

Proof

Utilizing properties of the indicator function established above, we have

\(I_B = \sum_{i = 1}^{n} I_{A_i} I_{C_i}\)

Note that since the \(A_i\) form a partition, we have \(\sum_{i = 1}^{n} I_{A_i} = 1\), so that the indicator function for the complementary event is

\(I_{B^c} = 1 - \sum_{i = 1}^{n} I_{A_i} I_{C_i} = \sum_{i = 1}^{n} I_{A_i} - \sum_{i = 1}^{n} I_{A_i} I_{C_i} = \sum_{i = 1}^{n} [1 - I_{C_i}] = \sum_{i = 1}^{n} I_{A_i} I_{C_{i}^{c}}\)

The last sum is the indicator function for \(\bigvee_{i = 1}^{n} A_i C_{i}^{c}\)

A technical comment on the class of events

The class of events plays a central role in the intuitive background, the application, and the formal mathematical structure. Events have been modeled as subsets of the basic space of all possible outcomes of the trial or experiment. In the case of a finite number of outcomes, any subset can be taken as an event. In the general theory, involving infinite possibilities, there are some technical mathematical reasons for limiting the class of subsets to be considered as events. The practical needs are these:

1. If \(A\) is an event, its complementary set must also be an event.
2. If \({A_i : i \in J}\) is a finite or countable class of events, the union and the intersection of members of the class need to be events.

A simple argument based on DeMorgan's rules shows that if the class contains complements of all its sets and countable unions, then it contains countable intersections. Likewise, if it contains complements of all its sets and countable intersections, then it contains countable unions. A class of sets closed under complements and countable unions is known as a sigma algebra of sets. In a formal, measure-theoretic treatment, a basic assumption is that the class of events is a sigma algebra and the probability measure assigns probabilities to members of that class. Such a class is so general that it takes very sophisticated arguments to establish the fact that such a class does not contain all subsets. But precisely because the class is so general and inclusive in ordinary applications we need not be concerned about which sets are permissible as events

A primary task in formulating a probability problem is identifying the appropriate events and the relationships between them. The theoretical treatment shows that we may work with great freedom in forming events, with the assurrance that in most applications a set so produced is a mathematically valid event. The so called measurability question only comes into play in dealing with random processes with continuous parameters. Even there, under reasonable assumptions, the sets produced will be events.