1.2: Probability Systems

Probability measures

In the module "Likelihood" we introduce the notion of a basic space ΩΩ of all possible outcomes of a trial or experiment, events as subsets of the basic space determined by appropriate characteristics of the outcomes, and logical or Boolean combinations of the events (unions, intersections, and complements) corresponding to logical combinations of the defining characteristics.

Occurrence or nonoccurrence of an event is determined by characteristics or attributes of the outcome observed on a trial. Performing the trial is visualized as selecting an outcome from the basic set. An event occurs whenever the selected outcome is a member of the subset representing the event. As described so far, the selection process could be quite deliberate, with a prescribed outcome, or it could involve the uncertainties associated with “chance.” Probability enters the picture only in the latter situation. Before the trial is performed, there is uncertainty about which of these latent possibilities will be realized. Probability traditionally is a number assigned to an event indicating the likelihood of the occurrence of that event on any trial.

We begin by looking at the classical model which first successfully formulated probability ideas in mathematical form. We use modern terminology and notation to describe it.

Classical probability

1. The basic space \(\Omega\) consists of a finite number N of possible outcomes.
   
   -There are thirty six possible outcomes of throwing two dice.
   -There are \(C(52,5) = \dfrac{52!}{5! 47!} = 2598960\) different hands of five cards (order not important).
   -There are \(2^5 = 32\) results (sequences of heads or tails) of flipping five coins.
2. Each possible outcome is assigned a probability 1/\(N\)
3. If event (subset) \(A\) has \(N_A\) elements, then the probability assigned event \(A\) is

\(P(A) = N_A /N\) (i.e., the fraction favorable to \(A\))

With this definition of probability, each event \(A\) is assigned a unique probability, which may be determined by counting \(N_A\), the number of elements in \(A\) (in the classical language, the number of outcomes "favorable" to the event) and \(N\) the total number of possible outcomes in the sure event \(\Omega\).

Probabilities for hands of cards

Consider the experiment of drawing a hand of five cards from an ordinary deck of 52 playing cards. The number of outcomes, as noted above, is \(N = C(52,5) = 2598960 N = C(52,5) = 2598960\). What is the probability of drawing a hand with exactly two aces? What is the probability of drawing a hand with two or more aces? What is the probability of not more than one ace?

Solution

Let \(A\) be the event of exactly two aces, \(B\) be the event of exactly three aces, and \(C\) be the event of exactly four aces. In the first problem, we must count the number \(N_A\) of ways of drawing a hand with two aces. We select two aces from the four, and select the other three cards from the 48 non aces. Thus

\(N_A = C(4, 2) C(48,3) = 103776\), so that \(P(A) = \dfrac{N_A}{N} = \dfrac{103776}{2598960} \approx 0.0399\)

There are two or more aces iff there are exactly two or exactly three or exactly four. Thus the event \(D\) of two or more is \(D = A \bigvee B \bigvee C\), since \(A, B, C\) are mutually exclusive,

\(N_D = N_A + N_b + N_c = C(4, 2) C(48, 3) + C(4, 3) C(48, 2) + C(4, 4) C(48, 1) = 103776 + 4512 + 48 = 108336\)

so that \(P(D) \approx 0.0417\). There is one ace or none iff there are not two or more aces. We thus want \(P(D^c)\). Now the number in \(D_c\) is the number not in \(D\) which is \(N - N_D\), so that

\(P(D^c) = \dfrac{N - N_D}{N} = 1 - \dfrac{N_D}{N} = 1 - P(D) = 0.9583\)

This example illustrates several important properties of the classical probability.

\(P(A) = N_A / N\) is a nonnegative quantity.
\(P(\Omega) = N/N = 1\)
If \(A, B, C\) are mutually exclusive, then the number in the disjoint union is the sum of the numbers in the individual events, so that

\(P(A \bigvee B \bigvee C) = P(A) + P(B) + P(C)\)

Several other elementary properties of the classical probability may be identified. It turns out that they can be derived from these three. Although the classical model is highly useful, and an extensive theory has been developed, it is not really satisfactory for many applications (the communications problem, for example). We seek a more general model which includes classical probability as a special case and is thus an extension of it. We adopt the Kolmogorov model (introduced by the Russian mathematician A. N. Kolmogorov) which captures the essential ideas in a remarkably successful way. Of course, no model is ever completely successful. Reality always seems to escape our logical nets.

The Kolmogorov model is grounded in abstract measure theory. A full explication requires a level of mathematical sophistication inappropriate for a treatment such as this. But most of the concepts and many of the results are elementary and easily grasped. And many technical mathematical considerations are not important for applications at the level of this introductory treatment and may be disregarded. We borrow from measure theory a few key facts which are either very plausible or which can be understood at a practical level. This enables us to utilize a very powerful mathematical system for representing practical problems in a manner that leads to both insight and useful strategies of solution.

Our approach is to begin with the notion of events as sets introduced above, then to introduce probability as a number assigned to events subject to certain conditions which become definitive properties. Gradually we introduce and utilize additional concepts to build progressively a powerful and useful discipline. The fundamental properties needed are just those illustrated in Example for the classical case.

Definition

A probability system consists of a basic set \(\Omega\) of elementary outcomes of a trial or experiment, a class of events as subsets of the basic space, and a probability measure \(P(\cdot)\) which assigns values to the events in accordance with the following rules

(P1): For any event \(A\), the probability \(P(A) \ge 0\).
(P2): The probability of the sure event \(P(\Omega) = 1\).
(P3): Countable additivity. If \({A_i : 1 \in J}\) is a mutually exclusive, countable class of events, then the probability of the disjoint union is the sum of the individual probabilities.

The necessity of the mutual exclusiveness (disjointedness) is illustrated in Example. If the sets were not disjoint, probability would be counted more than once in the sum. A probability, as defined, is abstract—simply a number assigned to each set representing an event. But we can give it an interpretation which helps to visualize the various patterns and relationships encountered. We may think of probability as mass assigned to an event. The total unit mass is assigned to the basic set \(\Omega\). The additivity property for disjoint sets makes the mass interpretation consistent. We can use this interpretation as a precise representation. Repeatedly we refer to the probability mass assigned a given set. The mass is proportional to the weight, so sometimes we speak informally of the weight rather than the mass. Now a mass assignment with three properties does not seem a very promising beginning. But we soon expand this rudimentary list of properties. We use the mass interpretation to help visualize the properties, but are primarily concerned to interpret them in terms of likelihoods.

(P4): \(P(A^c) = 1 - P(A)\). The follows from additivity and the fact that

\(1 = P(\Omega) = P(A \bigvee A^c) = P(A) + P(A^c)\)

(P5): \(P(\emptyset) = 0\). The empty set represents an impossible event. It has no members, hence cannot occur. It seems reasonable that it should be assigned zero probability (mass). Since \(\emptyset = \Omega^c\), this follows logically from P(4) and (P2).

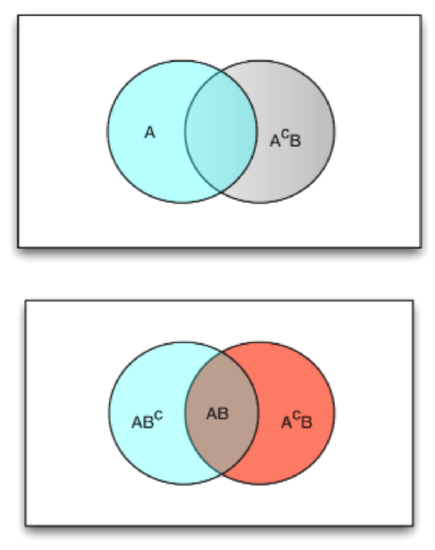
Figure 1.2.1: Partitions of the union \(A \cup B\)

(P6): If \(A \subset B\), then \(P(A) \le P(B)\). From the mass point of view, every point in \(A\) is also in \(B\), so that \(B\) must have at least as much mass as \(A\). Now the relationship \(A \subset B\) means that if \(A\) occurs, \(B\) must also. Hence \(B\) is at least as likely to occur as \(A\). From a purely formal point of view, we have

\(B = A \bigvee A^c B\) so that \(P(B) = P(A) + P(A^c B) \ge P(A)\) since \(P(A^c B) \ge 0\)

(P7):\(P(A \cup B) = P(A) + P(A^c B) = P(B) + P(AB^c) = P(AB^c) + P(AB) + P(A^cB)\)

\(= P(A) + P(B) - P(AB)\)

The first three expressions follow from additivity and partitioning of \(A \cup B\) as follows (see Figure 1.2.1).

\(A \cup B = A \bigvee A^c B = B \bigvee AB^c = AB^c \bigvee AB \bigvee A^c B\)

If we add the first two expressions and subtract the third, we get the last expression. In terms of probability mass, the first expression says the probability in \(A \cup B\) is the probability mass in \(A\) plus the additional probability mass in the part of \(B\) which is not in \(A\). A similar interpretation holds for the second expression. The third is the probability in the common part plus the extra in \(A\) and the extra in \(B\). If we add the mass in \(A\) and \(B\) we have counted the mass in the common part twice. The last expression shows that we correct this by taking away the extra common mass.

(P8): If \({B_i : i \in J}\) is a countable, disjoint class and \(A\) is contained in the union, then

\(A = \bigvee_{i \in J} AB_i\) so that \(P(A) = \sum_{i \in J} P(AB_i)\)

(P9): Subadditivity. If \(A = \bigcup_{i = 1}^{\infty} A_i\), then \(P(A) \le \sum_{i = 1}^{\infty} P(A_i)\). This follows from countable additivity, property (P6), and the fact

(Partitions)

\(A = \bigcup_{i = 1}^{\infty} A_i = \bigvee_{i = 1}^{\infty} B_i\), where \(B_i = A_i A_1^c A_2^c \cdot\cdot\cdot A_{i - 1}^c \subset A_i\)

This includes as a special case the union of a finite number of events.

Some of these properties, such as (P4), (P5), and (P6), are so elementary that it seems they should be included in the defining statement. This would not be incorrect, but would be inefficient. If we have an assignment of numbers to the events, we need only establish (P1), (P2), and (P3) to be able to assert that the assignment constitutes a probability measure. And the other properties follow as logical consequences.

Flexibility at a price

In moving beyond the classical model, we have gained great flexibility and adaptability of the model. It may be used for systems in which the number of outcomes is infinite (countably or uncountably). It does not require a uniform distribution of the probability mass among the outcomes. For example, the dice problem may be handled directly by assigning the appropriate probabilities to the various numbers of total spots, 2 through 12. As we see in the treatment of conditional probability, we make new probability assignments (i.e., introduce new probability measures) when partial information about the outcome is obtained.

But this freedom is obtained at a price. In the classical case, the probability value to be assigned an event is clearly defined (although it may be very difficult to perform the required counting). In the general case, we must resort to experience, structure of the system studied, experiment, or statistical studies to assign probabilities.

The existence of uncertainty due to “chance” or “randomness” does not necessarily imply that the act of performing the trial is haphazard. The trial may be quite carefully planned; the contingency may be the result of factors beyond the control or knowledge of the experimenter. The mechanism of chance (i.e., the source of the uncertainty) may depend upon the nature of the actual process or system observed. For example, in taking an hourly temperature profile on a given day at a weather station, the principal variations are not due to experimental error but rather to unknown factors which converge to provide the specific weather pattern experienced. In the case of an uncorrected digital transmission error, the cause of uncertainty lies in the intricacies of the correction mechanisms and the perturbations produced by a very complex environment. A patient at a clinic may be self selected. Before his or her appearance and the result of a test, the physician may not know which patient with which condition will appear. In each case, from the point of view of the experimenter, the cause is simply attributed to “chance.” Whether one sees this as an “act of the gods” or simply the result of a configuration of physical or behavioral causes too complex to analyze, the situation is one of uncertainty, before the trial, about which outcome will present itself.

If there were complete uncertainty, the situation would be chaotic. But this is not usually the case. While there is an extremely large number of possible hourly temperature profiles, a substantial subset of these has very little likelihood of occurring. For example, profiles in which successive hourly temperatures alternate between very high then very low values throughout the day constitute an unlikely subset (event). One normally expects trends in temperatures over the 24 hour period. Although a traffic engineer does not know exactly how many vehicles will be observed in a given time period, experience provides some idea what range of values to expect. While there is uncertainty about which patient, with which symptoms, will appear at a clinic, a physician certainly knows approximately what fraction of the clinic's patients have the disease in question. In a game of chance, analyzed into “equally likely” outcomes, the assumption of equal likelihood is based on knowledge of symmetries and structural regularities in the mechanism by which the game is carried out. And the number of outcomes associated with a given event is known, or may be determined.

In each case, there is some basis in statistical data on past experience or knowledge of structure, regularity, and symmetry in the system under observation which makes it possible to assign likelihoods to the occurrence of various events. It is this ability to assign likelihoods to the various events which characterizes applied probability. However determined, probability is a number assigned to events to indicate their likelihood of occurrence. The assignments must be consistent with the defining properties (P1), (P2), (P3) along with derived properties (P4) through (P9) (plus others which may also be derived from these). Since the probabilities are not “built in,” as in the classical case, a prime role of probability theory is to derive other probabilities from a set of given probabilites.