Search

Text Color

Margin Size

Font Type

Enable Dyslexic Font

20.6: Dimensional analysis

Last updated

Sep 4, 2024
Save as PDF
- 20.5: Time series
- 20.7: Estimating population size

$\newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}}$

$\newcommand{\id}{\mathrm{id}}$ $\newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$ $\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$ $\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\id}{\mathrm{id}}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\kernel}{\mathrm{null}\,}$

$\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$

$\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$

$\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$ $\newcommand{\AA}{\unicode[.8,0]{x212B}}$

$\newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$\newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$\newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vectorC}[1]{\textbf{#1}}$

$\newcommand{\vectorD}[1]{\overrightarrow{#1}}$

$\newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}}$

$\newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}}$

$\newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}}$

$\newcommand{\avec}{\mathbf a}$

$\newcommand{\bvec}{\mathbf b}$

$\newcommand{\cvec}{\mathbf c}$

$\newcommand{\dvec}{\mathbf d}$

$\newcommand{\dtil}{\widetilde{\mathbf d}}$

$\newcommand{\evec}{\mathbf e}$

$\newcommand{\fvec}{\mathbf f}$

$\newcommand{\nvec}{\mathbf n}$

$\newcommand{\pvec}{\mathbf p}$

$\newcommand{\qvec}{\mathbf q}$

$\newcommand{\svec}{\mathbf s}$

$\newcommand{\tvec}{\mathbf t}$

$\newcommand{\uvec}{\mathbf u}$

$\newcommand{\vvec}{\mathbf v}$

$\newcommand{\wvec}{\mathbf w}$

$\newcommand{\xvec}{\mathbf x}$

$\newcommand{\yvec}{\mathbf y}$

$\newcommand{\zvec}{\mathbf z}$

$\newcommand{\rvec}{\mathbf r}$

$\newcommand{\mvec}{\mathbf m}$

$\newcommand{\zerovec}{\mathbf 0}$

$\newcommand{\onevec}{\mathbf 1}$

$\newcommand{\real}{\mathbb R}$

$\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$

$\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$

$\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$

$\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$

$\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$

$\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$

$\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$

$\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$

$\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$

$\newcommand{\laspan}[1]{\text{Span}\{#1\}}$

$\newcommand{\bcal}{\cal B}$

$\newcommand{\ccal}{\cal C}$

$\newcommand{\scal}{\cal S}$

$\newcommand{\wcal}{\cal W}$

$\newcommand{\ecal}{\cal E}$

$\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$

$\newcommand{\gray}[1]{\color{gray}{#1}}$

$\newcommand{\lgray}[1]{\color{lightgray}{#1}}$

$\newcommand{\rank}{\operatorname{rank}}$

$\newcommand{\row}{\text{Row}}$

$\newcommand{\col}{\text{Col}}$

$\renewcommand{\row}{\text{Row}}$

$\newcommand{\nul}{\text{Nul}}$

$\newcommand{\var}{\text{Var}}$

$\newcommand{\corr}{\text{corr}}$

$\newcommand{\len}[1]{\left|#1\right|}$

$\newcommand{\bbar}{\overline{\bvec}}$

$\newcommand{\bhat}{\widehat{\bvec}}$

$\newcommand{\bperp}{\bvec^\perp}$

$\newcommand{\xhat}{\widehat{\xvec}}$

$\newcommand{\vhat}{\widehat{\vvec}}$

$\newcommand{\uhat}{\widehat{\uvec}}$

$\newcommand{\what}{\widehat{\wvec}}$

$\newcommand{\Sighat}{\widehat{\Sigma}}$

$\newcommand{\lt}{<}$

$\newcommand{\gt}{>}$

$\newcommand{\amp}{&}$

$\definecolor{fillinmathshade}{gray}{0.9}$

draft

Introduction

Cluster analysis or clustering is a multivariate analysis technique that includes a number of different algorithms for grouping objects in such a way that objects in the same group (called a cluster) are more similar to each other than they are to objects in other groups. A number of approaches have been taken, but loosely can be grouped into distance clustering methods (see Chapter 16.6 – Similarity and Distance) and linkage clustering methods: Distance methods involve calculating the distance (or similarity) between two points and whereas linkage methods involve calculating distances among the clusters. Single linkage involves calculating the distance among all pairwise comparisons between two clusters, then

Cluster analysis is common to molecular biology and phylogeny construction and more generally is an approach in use for exploratory data mining. Unsupervised machine learning (see 20.14 – Binary classification) used to classify, for example, methylation status of normal and diseased tissues from arrays (Clifford et al 2011)

Results from cluster analyses are often displayed as dendrograms. Clustering methods include a number of different algorithms hierarchical clustering: single-linkage clustering; complete linkage clustering; average linkage clustering (UPGMA) centroid based clustering: k-means clustering

R packages

factoextra

psa package from MorphoFun/psa/

Principal component analysis

Bumpus data from MorphoFun/psa, variable names changed.

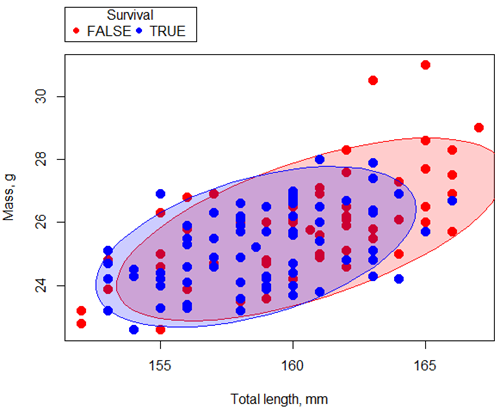
Scatterplot of English swallow mass in grams vs. total length of swallow in millimeters, colored blue for survival following winter storm and red for failure to survive the storm. An ellipse for each color encloses 90% of the data points for the respective group. — Figure $\PageIndex{1}$ : Scatterplot of English swallow mass (g) vs. total length (mm), by survival following winter storm.

R code for graph

scatterplot(Weight~Total_length | Survival, regLine=FALSE, smooth=FALSE, boxplots=FALSE,
ellipse=list(levels=c(.9)), by.groups=TRUE, grid=FALSE, pch=c(19,19), cex=1.5, col=c("red","blue"), xlab="Total length, mm", ylab="Mass, g", data=Bumpus)

Data ellipse — 90% of the pairwise points (red, did not survive; blue, did survive), not a confidence ellipse

Bumpus measured several traits, we want to use all of the data. However, highly correlated (Fig. $\PageIndex{2}$ ) and therefore multicollinear.

Scatterplot matrix of Bumpus data on English sparrow traits. — Figure $\PageIndex{2}$ : Scatterplot matrix of Bumpus English sparrow traits. Traits were (left-right): Alar extent (mm), length (tip of beak to tip of tail), length of head (mm), length of femur (in.), length of humerus (in.), length of sternum (in.), skull width (in.), length of tibio-taurus (in.), and weight (g).

R code for graph:

scatterplotMatrix(~Alar_extent+Beak_head_Length+Femur+Humerus+Keel_Length+Skull_width+Tibiotarsus+Total_length+Weight, 
regLine=FALSE, smooth=FALSE, diagonal=list(method="density"), data=Bumpus)

Note:

In Chapter 4, we discussed the importance of white space and Y-scale for graphs that make comparisons. Figure $\PageIndex{2}$ is a good example of where we trade-off the need for white space and concerns about telling the story — the various traits are positively correlated — against the dictum of an equal Y-scale for true comparisons.

Rcmdr: Statistics > Dimensional analysis > Principal component analysis …

.PC <-
princomp(~Alar_extent+Beak_head_Length+Femur+Humerus+Keel_Length+Skull_width+Tibiotarsus+Total_length+Weight, 
cor=TRUE, data=Bumpus)
cat("\nComponent loadings:\n")
print(unclass(loadings(.PC)))
cat("\nComponent variances:\n")
print(.PC\$sd^2)
cat("\n")
print(summary(.PC))
screeplot(.PC)
Bumpus <<- within(Bumpus, {
PC2 <- .PC\$scores[,2]
PC1 <- .PC\$scores[,1]
})
})

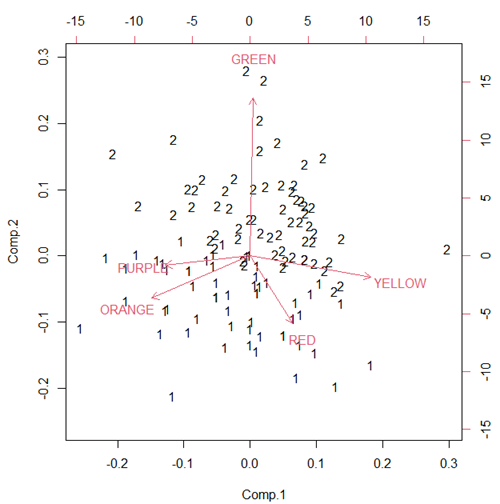
Importance of components

                              Comp.1     Comp.2
Standard deviation         2.3046882  0.9988978
Proportion of Variance     0.5901764  0.1108663
Cumulative Proportion      0.5901764  0.7010427

K-means clustering

Number of clusters

Iterations

Figure $\PageIndex{3}$ : Bi-plot of clusters by color from Skittles mini bags.

Ward’s method

Complete linkage

McQuitty’s method

Centroid linkage

A common way to depict the results of a cluster analysis is to construct a dendogram.

Questions

[pending]

References and further reading

Bumpus, H. C. (1898). Eleventh lecture. The elimination of the unfit as illustrated by the introduced sparrow, Passer domesticus. (A fourth contribution to the study of variation.). Biology Lectures: Woods Hole Marine Biological Laboratory, 209–255.

Clifford, H., Wessely, F., Pendurthi, S., & Emes, R. D. (2011). Comparison of clustering methods for investigation of genome-wide methylation array data. Frontiers in genetics, 2, 88.

Ferreira, L., & Hitchcock, D. B. (2009). A comparison of hierarchical methods for clustering functional data. Communications in Statistics-Simulation and Computation, 38(9), 1925-1949.

Fraley C, Raftery AE. (2002) Model-based clustering, discriminant analysis, and density estimation. J. Am. Stat. Assoc.; 97(458):611–31.