8.10: Additive MLR with more than two groups - Headache example

The same techniques can be extended to more than two groups. A study was conducted to explore sound tolerances using \(n = 98\) subjects with the data available in the Headache data set from the heplots package (Fox and Friendly 2021). Each subject was initially exposed to a tone, stopping when the tone became definitely intolerable (DU) and that decibel level was recorded (variable called du1). Then the subjects were randomly assigned to one of four treatments: T1 (Listened again to the tone at their initial DU level, for the same amount of time they were able to tolerate it before); T2 (Same as T1, with one additional minute of exposure); T3 (Same as T2, but the subjects were explicitly instructed to use the relaxation techniques); and Control (these subjects experienced no further exposure to the noise tone until the final sensitivity measures were taken). Then the DU was measured again (variable called du2). One would expect that there would be a relationship between the upper tolerance levels of the subjects before and after treatment. But maybe the treatments impact that relationship? We can use our indicator approach to see if the treatments provide a shift to higher tolerances after accounting for the relationship between the two measurements¹⁵¹. The scatterplot¹⁵² of the results in Figure 8.26 shows some variation in the slopes and the intercepts for the groups although the variation in intercepts seems more prominent than differences in slopes. Note that the fct_relevel function was applied to the treatment variable with an option of "Control" to make the Control category the baseline category as the person who created the data set had set T1 as the baseline in the treatment variable.

library(heplots)
data(Headache)
Headache <- as_tibble(Headache)
Headache

## # A tibble: 98 × 6
##    type    treatment    u1   du1    u2   du2
##    <fct>   <fct>     <dbl> <dbl> <dbl> <dbl>
##  1 Migrane T3         2.34  5.3   5.8   8.52
##  2 Migrane T1         2.73  6.85  4.68  6.68
##  3 Tension T1         0.37  0.53  0.55  0.84
##  4 Migrane T3         7.5   9.12  5.7   7.88
##  5 Migrane T3         4.63  7.21  5.63  6.75
##  6 Migrane T3         3.6   7.3   4.83  7.32
##  7 Migrane T2         2.45  3.75  2.5   3.18
##  8 Migrane T1         2.31  3.25  2     3.3 
##  9 Migrane T1         1.38  2.33  2.23  3.98
## 10 Tension T3         0.85  1.42  1.37  1.89
## # … with 88 more rows
## # ℹ Use `print(n = ...)` to see more rows

Headache <- Headache %>% mutate(treatment = factor(treatment),
                                treatment = fct_relevel(treatment, "Control")
                                )
# Make treatment a factor and Control the baseline category
Headache %>% ggplot(mapping = aes(x = du1, y = du2, color = treatment, 
                                  shape = treatment)) +
  geom_smooth(method = "lm", se = F) + 
  geom_point(size = 2.5) +
  theme_bw() +
  scale_color_viridis_d(end = 0.85, option = "inferno") + 
  labs(title = "Scatterplot of Maximum DB tolerance before & 
       after treatment (by treatment)")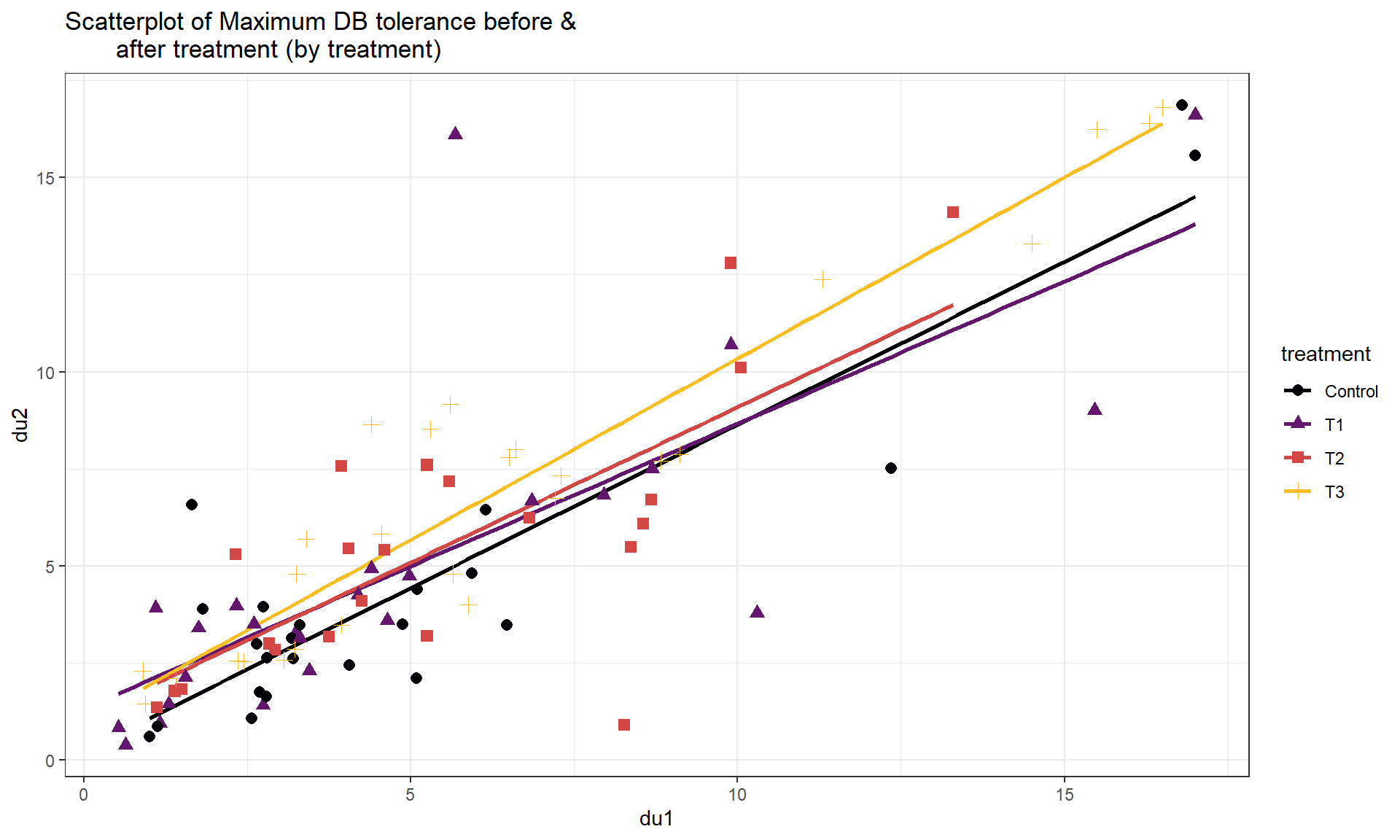

Figure 8.26: Scatterplot of post-treatment decibel tolerance (du2) vs pre-treatment tolerance (du1) by treatment level (4 groups).

This data set contains a categorical variable with 4 levels. To go beyond two groups, we have to add more than one indicator variable, defining three indicators to turn on (1) or off (0) for three of the levels of the variable with the same reference level used for all the indicators. For this example, the Control group is chosen as the baseline group so it hides in the background while we define indicators for the other three levels. The indicators for T1, T2, and T3 treatment levels are:

• Indicator for T1: \(I_{T1,i} = \left\{\begin{array}{rl} 1 & \text{if Treatment} = T1 \\ 0 & \text{else} \end{array}\right.\)
• Indicator for T2: \(I_{T2,i} = \left\{\begin{array}{rl} 1 & \text{if Treatment} = T2 \\ 0 & \text{else} \end{array}\right.\)
• Indicator for T3: \(I_{T3,i} = \left\{\begin{array}{rl} 1 & \text{if Treatment} = T3 \\ 0 & \text{else} \end{array}\right.\)

We can see the values of these indicators for a few observations and their original variable (treatment) in the following output. For Control all the indicators stay at 0.

Treatment	I_T1	I_T2	I_T3
T3	0	0	1
T1	1	0	0
T1	1	0	0
T3	0	0	1
T3	0	0	1
T3	0	0	1
T2	0	1	0
T1	1	0	0
T1	1	0	0
T3	0	0	1
T3	0	0	1
T2	0	1	0
T3	0	0	1
T1	1	0	0
T3	0	0	1
Control	0	0	0
T3	0	0	1

When we fit the additive model of the form y ~ x + group, the lm function takes the \(\boldsymbol{J}\) categories and creates \(\boldsymbol{J-1}\) indicator variables. The baseline level is always handled in the intercept. The true model will be of the form

\[y_i = \beta_0 + \beta_1x_i +\beta_2I_{\text{Level}2,i}+\beta_3I_{\text{Level}3,i} +\cdots+\beta_{J}I_{\text{Level}J,i}+\varepsilon_i\]

where the \(I_{\text{CatName}j,i}\text{'s}\) are the different indicator variables. Note that each indicator variable gets a coefficient associated with it and is “turned on” whenever the \(i^{th}\) observation is in that category. At most only one of the \(I_{\text{CatName}j,i}\text{'s}\) is a 1 for any observation, so the \(y\)-intercept will either be \(\beta_0\) for the baseline group or \(\beta_0+\beta_j\) for \(j = 2,\ldots,J\). It is important to remember that this is an “additive” model since the effects just add and there is no interaction between the grouping variable and the quantitative predictor. To be able to trust this model, we need to check that we do not need different slope coefficients for the groups as discussed in the next section.

For these types of models, it is always good to start with a plot of the data set with regression lines for each group – assessing whether the lines look relatively parallel or not. In Figure 8.26, there are some differences in slopes – we investigate that further in the next section. For now, we can proceed with fitting the additive model with different intercepts for the four levels of treatment and the quantitative explanatory variable, du1.

head1 <- lm(du2 ~ du1 + treatment, data = Headache)
summary(head1)

## 
## Call:
## lm(formula = du2 ~ du1 + treatment, data = Headache)
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -6.9085 -0.9551 -0.3118  1.1141 10.5364 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)
## (Intercept)  0.25165    0.51624   0.487   0.6271
## du1          0.83705    0.05176  16.172   <2e-16
## treatmentT1  0.55752    0.61830   0.902   0.3695
## treatmentT2  0.63444    0.63884   0.993   0.3232
## treatmentT3  1.36671    0.60608   2.255   0.0265
## 
## Residual standard error: 2.14 on 93 degrees of freedom
## Multiple R-squared:  0.7511, Adjusted R-squared:  0.7404 
## F-statistic: 70.16 on 4 and 93 DF,  p-value: < 2.2e-16

The complete estimated regression model is

\[\widehat{\text{du2}}_i = 0.252+0.837\cdot\text{du1}_i +0.558I_{\text{T1},i}+0.634I_{\text{T2},i}+1.367I_{\text{T3},i}\]

For each group, the model simplifies to an SLR as follows:

• For Control (baseline):

\[\begin{array}{rl} \widehat{\text{du2}}_i & = 0.252+0.837\cdot\text{du1}_i +0.558I_{\text{T1},i}+0.634I_{\text{T2},i}+1.367I_{\text{T3},i} \\ & = 0.252+0.837\cdot\text{du1}_i+0.558*0+0.634*0+1.367*0 \\ & = 0.252+0.837\cdot\text{du1}_i. \end{array}\]

• For T1:

\[\begin{array}{rl} \widehat{\text{du2}}_i & = 0.252+0.837\cdot\text{du1}_i +0.558I_{\text{T1},i}+0.634I_{\text{T2},i}+1.367I_{\text{T3},i} \\ & = 0.252+0.837\cdot\text{du1}_i+0.558*1+0.634*0+1.367*0 \\ & = 0.252+0.837\cdot\text{du1}_i + 0.558 \\ & = 0.81+0.837\cdot\text{du1}_i. \end{array}\]

• Similarly for T2:

\[\widehat{\text{du2}}_i = 0.886 + 0.837\cdot\text{du1}_i\]

• Finally for T3:

\[\widehat{\text{du2}}_i = 1.62 + 0.837\cdot\text{du1}_i\]

To reinforce what this additive model is doing, Figure 8.27 displays the estimated regression lines for all four groups, showing the shifts in the y-intercepts among the groups.

Figure 8.27: Plot of estimated noise tolerance additive model.

The right panel of the term-plot (Figure 8.28) shows how the T3 group seems to have shifted up the most relative to the others and the Control group seems to have a mean that is a bit lower than the others, in the model that otherwise assumes that the same linear relationship holds between du1 and du2 for all the groups. After controlling for the Treatment group, for a 1 decibel increase in initial tolerances, we estimate, on average, to obtain a 0.84 decibel change in the second tolerance measurement. The R² shows that this is a decent model for the responses, with this model explaining 75.1% percent of the variation in the second decibel tolerance measure. We should check the diagnostic plots and VIFs to check for any issues – all the diagnostics and assumptions are as before except that there is no assumption of linearity between the grouping variable and the responses. Additionally, sometimes we need to add group information to diagnostics to see if any patterns in residuals look different in different groups, like linearity or non-constant variance, when we are fitting models that might contain multiple groups.

plot(allEffects(head1, residuals = T), grid = T)

Figure 8.28: Term-plots of the additive decibel tolerance model with partial residuals.

The diagnostic plots in Figure 8.29 provides some indications of a few observations in the tails that deviate from a normal distribution to having slightly heavier tails but only one outlier is of real concern and causes some concern about the normality assumption. There is a small indication of increasing variability as a function of the fitted values as both the Residuals vs. Fitted and Scale-Location plots show some fanning out for higher values but this is a minor issue. There are no influential points here since all the Cook’s D values are less than 0.5.

par(mfrow = c(2,2), oma = c(0,0,3,0))
plot(head1, pch = 16, sub.caption = "")
title(main="Plot of diagnostics for additive model with du1 and 
     treatment for du2", outer=TRUE)

Figure 8.29: Diagnostic plots for the additive decibel tolerance model.

Additionally, sometimes we need to add group information to diagnostics to see if any patterns in residuals look different in different groups, like linearity or non-constant variance, when we are fitting models that might contain multiple groups. We can use the same scatterplot tools to make our own plot of the residuals (extracted using the residuals function) versus the fitted values (extracted using the fitted function) by groups as in Figure 8.30. This provides an opportunity to introduce faceting, where we can split our plots into panels by a grouping variable, here by the treatment applied to each subject. This can be helpful with multiple groups to be able to see each one more clearly as we avoid overplotting. The addition of + facet_grid(cols = vars(treatment)) facets the plot based on the treatment variable and puts the facets in different columns because of the cols = part of the code (rows = specifies the number of rows for the facets), labeling each panel at the top with the level being displayed of the faceting variable (vars() is needed to help ggplot find the variable). In this example, there are no additional patterns identified by making this plot although we do see some minor deviations in the fitted lines for each group, but it is a good additional check in these multi-group situations.

Headache <- Headache %>% mutate(resids = residuals(head1),
                                fits = fitted(head1)
                                )
Headache %>% ggplot(mapping = aes(x = fits, y = resids, 
                                  color = treatment, shape = treatment)) +
  geom_smooth(method = "lm", se = F) +
  geom_point(size = 2.5) +
  theme_bw() +
  scale_color_viridis_d(end = 0.85, option = "inferno") +
  labs(title = "Scatterplot of Residuals vs Fitted by Treatment Group") +
  facet_grid(cols = vars(treatment))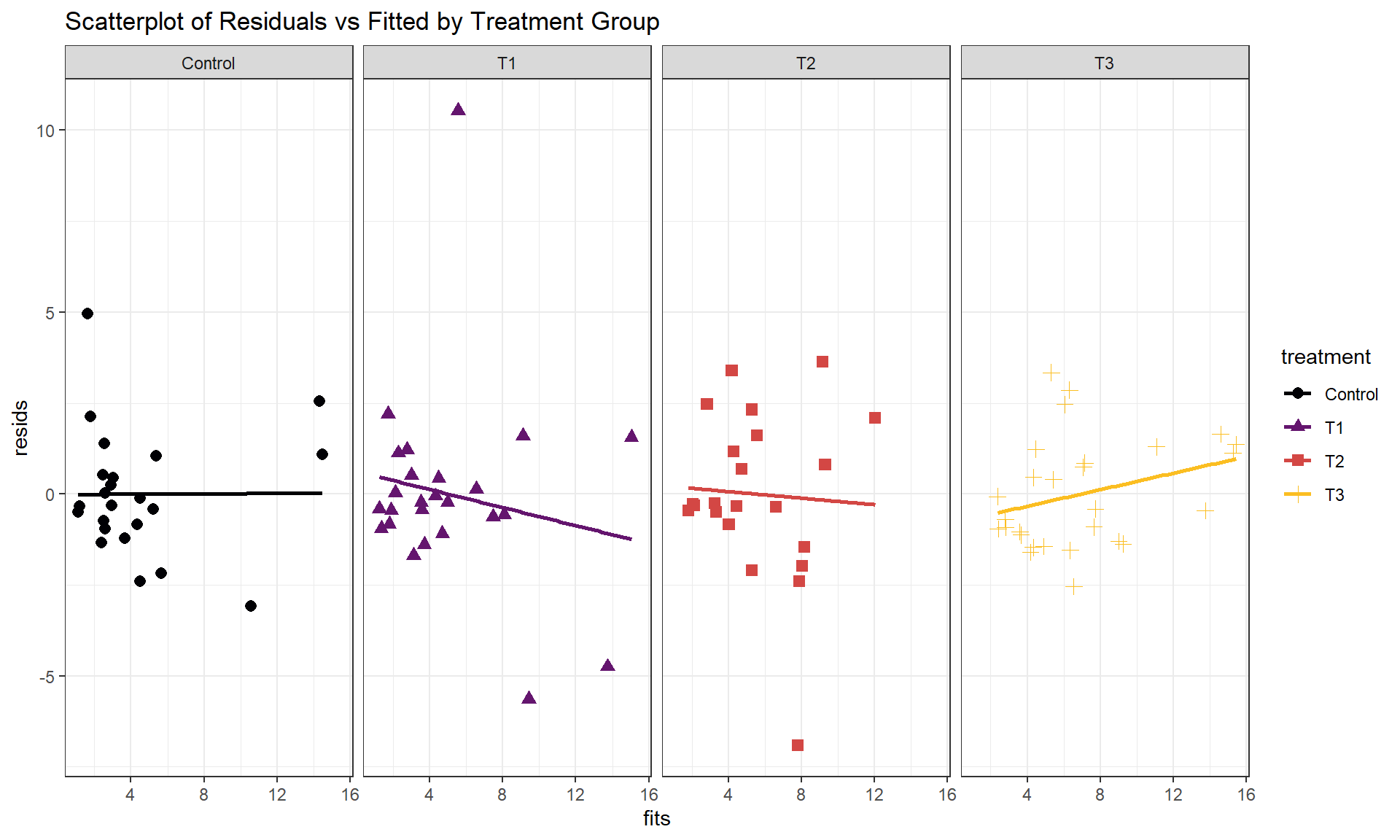

Figure 8.30: Faceted scatterplot of residuals versus fitted values by treatment group from the additive decibel tolerance model.

The VIFs are different for models with categorical variables than for models with only quantitative predictors in MLR, even though we are still concerned with shared information across the predictors of all kinds. For categorical predictors, the \(J\) levels are combined to create a single measure for the predictor all together called the generalized VIF (GVIF). For GVIFs, interpretations are based on the GVIF measure to the power \(1/(2*(J-1))\). For quantitative predictors when GVIFS are present, \(J\) = 2, and the power simplifies to \(1/2\), which is our regular square-root scale for inflation of standard errors due to multicollinearity (so the GVIF is the VIF for quantitative predictors). For a \(J\)-level categorical predictor, the power is also \(1/2\) for \(J=2\) levels and increases for more levels. There are no rules of thumb for GVIFs for \(J>2\). In the following output, there are four levels, so \(J=4\). When raised to the requisite power, the GVIF interpretation for multi-category categorical predictors is the multiplicative increase in the SEs for the coefficients on all the indicator variables due to multicollinearity with other predictors. In this model, the SE for the quantitative predictor du1 is 1.009 times larger due to multicollinearity with other predictors and the SEs for the indicator variables for the four-level categorical treatment predictor are 1.003 times larger due to multicollinearity, both compared to what they would have been with no shared information in the predictors in the model. Neither are large, so multicollinearity is not a problem in this model.

vif(head1)

##              GVIF Df GVIF^(1/(2*Df))
## du1       1.01786  1        1.008891
## treatment 1.01786  3        1.002955

While there are inferences available in the model output, the tests for the indicator variables are not too informative (at least to start) since they only compare each group to the baseline. In Section 8.12, we see how to use ANOVA F-tests to help us ask general questions about including a categorical predictor in the model. But we can compare adjusted R² values with and without Treatment to see if including the categorical variable was “worth it”:

head1R <- lm(du2 ~ du1, data = Headache)

summary(head1R)

## 
## Call:
## lm(formula = du2 ~ du1, data = Headache)
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -6.9887 -0.8820 -0.2765  1.1529 10.4165 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)
## (Intercept)  0.84744    0.36045   2.351   0.0208
## du1          0.85142    0.05189  16.408   <2e-16
## 
## Residual standard error: 2.165 on 96 degrees of freedom
## Multiple R-squared:  0.7371, Adjusted R-squared:  0.7344 
## F-statistic: 269.2 on 1 and 96 DF,  p-value: < 2.2e-16

The adjusted R² in the model with both Treatment and du1 is 0.7404 and the adjusted R² for this reduced model with just du1 is 0.7344, suggesting the Treatment is useful. The next section provides a technique to be able to work with different slopes on the quantitative predictor for each group. Comparing those results to the results for the additive model allows assessment of the assumption in this section that all the groups had the same slope coefficient for the quantitative variable.