12.5: Try It!

Exercise \(\PageIndex{1}\)

Ginkgo Biloba is recognized as a herbal remedy for memory improvement. To investigate its effectiveness on memory recall, a cross-over study was planned using 3 treatments: one tablet of 120mg Ginkgo Biloba (G), one tablet of 200mg Caffeine pill (C), and sleep for 2 hours before the recall test (S). The assignment order of the 3 treatments to participants was determined by randomly assigning 12 college students to one of 6 possible sequences of the 3 treatments. The student recall capability was assessed based on a Recall score and the 3 treatments were given over 3 consecutive days. On each day, only one treatment was administered before one 1 hour of taking the recall test at 2.00 pm (the higher the recall score the better).

a) Which variable signifies the experimental unit?

Solution

Id

b) What is the washout period?

Solution

One day

c) How many periods are required?

Solution

3

d) How many replicates are there?

Solution

2

e) Perform a statistical analysis to determine if the treatments vary with regard to memory recall. The data can be found in Cross_over_Ex1.txt

Solution: Using SAS

DATA CROSS_OVER;
INPUT score  Seq $ PER  Id  TRT $ X1  X2;
DATALINES;
74  CGS  1  1  C  0  0
45  CGS  1  2  C  0  0
92  CSG  1  3  C  0  0
94  CSG  1  4  C  0  0
79  GCS  1  5  G  0  0
35  GCS  1  6  G  0  0
31  GSC  1  7  G  0  0
40  GSC  1  8  G  0  0
106  SCG  1  9  S  0  0
60  SCG  1  10  S  0  0
80  SGC  1  11  S  0  0
110  SGC  1  12  S  0  0
41  CGS  2  1  G  1  0
20  CGS  2  2  G  1  0
50  CSG  2  3  S  1  0
88  CSG  2  4  S  1  0
92  GCS  2  5  C  0  1
50  GCS  2  6  C  0  1
32  GSC  2  7  S  0  1
54  GSC  2  8  S  0  1
120  SCG  2  9  C  -1  -1
80  SCG  2  10  C  -1  -1
75  SGC  2  11  G  -1  -1
55  SGC  2  12  G  -1  -1
64  CGS  3  1  S  0  1
30  CGS  3  2  S  0  1
55  CSG  3  3  G  -1  -1
55  CSG  3  4  G  -1  -1
76  GCS  3  5  S  1  0
50  GCS  3  6  S  1  0
38  GSC  3  7  C  -1  -1
66  GSC  3  8  C  -1  -1
85  SCG  3  9  G  1  0
40  SCG  3  10  G  1  0
88  SGC  3  11  C  0  1
86  SGC  3  12  C  0  1
;
RUN;

proc mixed data=CROSS_OVER;
  class PER TRT SEQ  ID;
  model SCORE=PER  TRT SEQ  X1 X2 / ddfm=kr;
  repeated PER /subject=ID(SEQ) type=cs rcorr;
  ods output FitStatistics=FitCS (rename=(value=CS)) FitStatistics=FitCSp;
  title 'Compound Symmetry';
run;
title ' '; run;

proc mixed data=CROSS_OVER;
  class PER TRT SEQ  ID;
  model SCORE=PER  TRT SEQ  X1 X2 / ddfm=kr;
  repeated PER /subject=ID(SEQ) type=AR(1) rcorr;
  ods output FitStatistics=FitAR1 (rename=(value=AR1)) FitStatistics=FitAR1p;
  title 'Autoregressive Lag 1';
run;
title ' '; run;

proc mixed data=CROSS_OVER;
  class PER TRT SEQ  ID;
  model SCORE=PER  TRT SEQ  X1 X2 / ddfm=kr;
  repeated PER /subject=ID(SEQ) type=UN rcorr;
  ods output FitStatistics=FitUN (rename=(value=UN)) FitStatistics=FitUNp;
  title 'Unstructured';
run;
title ' '; run;

proc mixed data=CROSS_OVER;
  class PER TRT SEQ  ID;
  model SCORE=PER  TRT SEQ  X1 X2 / ddfm=kr;
  repeated PER /subject=ID(SEQ) type=CSH  rcorr;
  ods output FitStatistics=FitCSH (rename=(value=CSH)) FitStatistics=FitCSHp;
  title 'HETEROGENOUS COMPOUND SYMMETRY';
run;
title ' '; run;

data fits;
  merge FitCS FitAR1 FitUN FITCSH;
  by descr;
run;
ods listing; proc print data=fits; run; 

The above code was used to obtain the fit statistics for different covariance structures and the AICC (AIC and BIC) values indicate that CS is the best covariance structure. Hence, the remaining analysis was done using CS.

Obs	Descr	CS	AR1	UN	CSH
1	-2 Res Log Likelihood	215.3	219.1	212.7	214.7
2	AIC (Smaller is Better)	219.3	223.1	224.7	222.7
3	AICC (Smaller is Better)	219.9	223.7	229.7	224.8
4	BIC (Smaller is Better)	220.3	224.1	227.6	224.6

/* Model Adjusting for carryover effects */
proc mixed data= CROSS_OVER;
  class per TRT SEQ ID;
  model SCORE=PER  TRT SEQ  X1 X2 / ddfm=kr;
  repeated PER /subject=ID(SEQ) type=cs rcorr;
  store out_CROSS_OVER;
run;

proc plm restore=out_CROSS_OVER;
  lsmeans TRT / adjust=tukey plot=meanplot cl lines;
  ods exclude diffs diffplot;
run;

/* Reduced Model, Ignoring carryover effects */
proc mixed data= CROSS_OVER;
  class per TRT seq  ID;
  model SCORE=PER  TRT SEQ   / ddfm=kr;
  repeated PER /subject=ID(SEQ) type=cs rcorr;
  lsmeans TRT / pdiff adjust=tukey;
run; 

Full Model: with carryover effect

Fit Statistics
-2 Res Log Likelihood	215.3
AIC (Smaller is Better)	219.3
AICC (Smaller is Better)	219.9
BIC (Smaller is Better)	220.3

Type 3 Tests of Fixed Effects
Effect	Num DF	Den DF	F Value	Pr > F
PER	2	18	3.12	0.0688
TRT	2	18	18.03	<.0001
Seq	5	6.1	1.46	0.3259
X1	1	18	0.10	0.7565
X2	1	18	0.18	0.6768

Reduced Model: without carryover effect

Fit Statistics
-2 Res Log Likelihood	224.2
AIC (Smaller is Better)	228.2
AICC (Smaller is Better)	228.7
BIC (Smaller is Better)	229.1

Type 3 Tests of Fixed Effects
Effect	Num DF	Den DF	F Value	Pr > F
PER	2	20	3.36	0.0552
TRT	2	20	23.70	<.0001
Seq	5	6	1.52	0.3101

The test statistic below tests for the significance of the carry over effect. \(\Delta^{2} = \left(-2 \log L_{Reduced}\right) - \left(-2 \log L_{Full}\right) with \(df_{Full} - df_{Reduced}\) degrees of freedom.

\(\Delta^{2} = (224.2 - 215.3) = 8.9\). This exceeds the critical Chi-Square of 5.991 \(\left(\chi_{.05, 2}^{2}\right)\) indicating that model with carryover effect is more appropriate and will be used to base the final conclusions.

In the full model output, the Treatment is the only significant factor, so LSmeans and comparisons are generated only for the treatment effect. The results of the Tukey comparison procedure indicate that treatments C and S are not significantly different, but G is significantly lower, indicating that both sleep for 2 hours and caffeine are similarly effective in improving recall capability and are superior to Ginkgo biloba.

TRT Least Squares Means
TRT	Estimate	Standard Error	DF	t Value	Pr > |t|	Alpha	Lower	Upper
C	76.7222	6.2382	8.572	12.30	<.0001	0.05	62.5024	90.9421
G	50.4306	6.2382	8.572	8.08	<.0001	0.05	36.2107	64.6504
S	67.5139	6.2382	8.572	10.82	<.0001	0.05	53.2940	81.7337

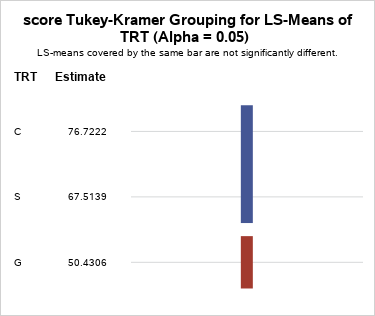
Figure \(\PageIndex{1}\): Scores for Tukey-Kramer grouping