16.2.2: Interpretation of the Chi-Square Goodness-of-Fit Test
- Page ID
- 17429
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)This is a long section, but it really helps you understand where the the Chi-Square Goodness of Fit comes from and what it means.
Goodness of Fit Test
The \(\chi^2\) Goodness of fit test is one of the oldest hypothesis tests around: it was invented by Karl Pearson around the turn of the century (Pearson 1900), with some corrections made later by Sir Ronald Fisher (Fisher 1922a). To introduce the statistical problem that it addresses, let’s start with some psychology…
Over the years, there have been a lot of studies showing that humans have a lot of difficulties in simulating randomness. Try as we might to “act” random, we think in terms of patterns and structure, and so when asked to “do something at random”, what people actually do is anything but random. As a consequence, the study of human randomness (or non-randomness, as the case may be) opens up a lot of deep psychological questions about how we think about the world. With this in mind, let’s consider a very simple study. Suppose I asked people to imagine a shuffled deck of cards, and mentally pick one card from this imaginary deck “at random”. After they’ve chosen one card, I ask them to mentally select a second one. For both choices, what we’re going to look at is the suit (hearts, clubs, spades or diamonds) that people chose. After asking, say, N=200 people to do this, I’d like to look at the data and figure out whether or not the cards that people pretended to select were really random. The data on the card that people pretended to select are shown in Table \(\PageIndex{1}\), called "Observed" for reasons that will become clear very soon:
| Card Suit Pretended to Choose: | Clubs ♣ | Diamonds ♢ | Hearts ♡ | Spades ♠ |
|---|---|---|---|---|
| Observed: | 35 | 51 | 64 | 50 |
This is called a contingency table, and shows that frequency of the different categories. Looking at it, there’s a bit of a hint that people might be more likely to select hearts than clubs, but it’s not completely obvious just from looking at it whether that’s really true, or if this is just due to chance. So we’ll probably have to do some kind of statistical analysis to find out, which is what I’m going to talk about in the next section.
Excellent. It’s also worth nothing that mathematicians prefer to talk about things in general rather than specific things, so you’ll also see the notation Oi, which refers to the number of observations that fall within the i-th category (where it could be 1, 2, or 3, or x, y, or z). This textbook has used these type of subscripts in the formulas, but then replaced them with letters relating to the name of the groups in the practice. So, if we want to refer to the set of all observed frequencies, statisticians group all of observed values into one variable, which we’ll refer to as O for Observed.
O=(O1,O2,O3,O4)
or
O=(OC,OD,OH,OS)
Again, there’s nothing new or interesting here: it’s just notation. If we say that O = (35,51,64,50) all we're doing is describing the table of observed frequencies (i.e., Table \(\PageIndex{1}\)), but we're referring to it using mathematical notation.
Hypotheses
Null Hypothesis
We'll start with null hypotheses for Chi-Square Goodness of Fit test because the null hypothesis will help us understand our more limited research hypothesis.
Our research question is whether people choose cards randomly or not. What we’re going to want to do now is translate this into some statistical hypotheses, and construct a statistical test of those hypotheses. In this case, the null hypothesis in words is that there is no pattern of relationship in the suits that participants pretended to choose; in other words, all four suits will be chosen with equal probability.
Now, because this is statistics, we have to be able to say the same thing in a mathematical way. If the null hypothesis is true, then each of the four suits has a 25% chance of being selected: in other words, our null hypothesis claims that PC=.25, PD=.25, PH=.25 and finally that PS=.25. However, in the same way that we can group our observed frequencies into a variable called O that summarizes the entire data set, we can use P to refer to the probabilities that correspond to our null hypothesis. So if I let the P=(P1,P2,P3,P4), or P = (PC, PD ,PH ,PS ) refers to the collection of probabilities that describe our null hypothesis, then we have
Null Hypothesis for \(P = (0.25, 0.25, 0.25, 0.25)\)
In this particular instance, our null hypothesis corresponds to a probabilities P in which all of the probabilities are equal to one another. But this doesn’t have to be the case. For instance, if the experimental task was for people to imagine they were drawing from a deck that had twice as many clubs as any other suit, then the null hypothesis would correspond to something like P=(0.4, 0.2, 0.2, 0.2). As long as the probabilities are all positive numbers, and they all sum to 1, them it’s a perfectly legitimate choice for the null hypothesis. However, the most common use of the Goodness of Fit test is to test a null hypothesis that all of the categories are equally likely, so we’ll stick to that for our example.
Research Hypothesis
What about our research hypothesis? All we’re really interested in is demonstrating that the probabilities involved aren’t all identical (that is, people’s choices weren’t completely random). As a consequence, the “human friendly” versions of our research hypothesis is that there is a pattern of relationship in the suits that participants pretended to choose. Another way to say this is that at least one of the suit-choice probabilities isn’t 0.25. This leads to the mathematical research hypothesis of:
Research Hypothesis of \( P\ne(0.25, 0.25, 0.25, 0.25)\)
The “Goodness of Fit” Test Statistic
At this point, we have our observed frequencies O and a collection of probabilities P corresponding the null hypothesis that we want to test. What we now want to do is construct a test of the null hypothesis. The basic trick that a Goodness of Fit test uses is to construct a test statistic that measures how “close” the data are to the null hypothesis. If the data don’t resemble what you’d “expect” to see if the null hypothesis were true, then it probably isn’t true. Okay, if the null hypothesis were true, what would we expect to see? Or, to use the correct terminology, what are the expected frequencies. There are N=200 observations, and (if the null is true) the probability of any one of them choosing a heart is PH = 0.25, so I guess we’re expecting 200 x 0.25=50 hearts, right? Or, more specifically, if we let E refer to “the number of responses from any one category that we’d expect if the null is true”, then
\(E = N \times P\)
This test is pretty easy to calculate, and we'll cover in the next sections. But to focus on what's happening: if there are 200 observation that can fall into four categories, and we think that all four categories are equally likely, then on average we’d expect to see 50 observations in each category, right?
Now, how do we translate this into a test statistic? Clearly, what we want to do is compare the expected number of observations in each category (Ei) with the observed number of observations in that category (Oi). And on the basis of this comparison, we ought to be able to come up with a good test statistic. To start with, let’s calculate the difference between what the null hypothesis expected us to find and what we actually did find. That is, we calculate the “observed minus expected” difference score, E-O (Expected minus Observed) for each category. In this scenario, the categories are the car suits. This is illustrated in the following table (Table \(\PageIndex{2}\)).
| Clubs ♣ | Diamonds ♢ | Hearts ♡ | Spades ♠ | |
|---|---|---|---|---|
| Observed Frequency (O) | 35 | 51 | 64 | 50 |
| Expected Frequency (E) | 50 | 50 | 50 | 50 |
| Difference Score (O Minus E) | 15 | -1 | -14 | 0 |
It’s clear that people chose more hearts and fewer clubs than the null hypothesis predicted. However, a moment’s thought suggests that these raw differences aren’t quite what we’re looking for. Intuitively, it feels like it’s just as bad when the null hypothesis predicts too few observations (which is what happened with hearts) as it is when it predicts too many (which is what happened with clubs). So it’s a bit weird that we have a negative number for clubs and a positive number for hearts. One easy way to fix this is to square everything, so that we now calculate the squared differences, (Ei−Oi)2. Let's see what that looks like in Table \(\PageIndex{3}\).
| Clubs ♣ | Diamonds ♢ | Hearts ♡ | Spades ♠ | |
|---|---|---|---|---|
| Observed Frequency (O) | 35 | 51 | 64 | 50 |
| Expected Frequency (E) | 50 | 50 | 50 | 50 |
| Difference Score (O Minus E) | 15 | -1 | -14 | 0 |
| Difference Score Squared | \(15^2 = 225\) | \((-1)^2 = 1\) |
\((-14)^2 = 196\) |
\(0^2 = 0\) |
Now we’re making progress. What we’ve got now is a collection of numbers that are big whenever the null hypothesis makes a bad prediction (clubs and hearts), but are small whenever it makes a good one (diamonds and spades). Next, for some technical reasons that I’ll explain in a moment, let’s also divide all these numbers by the expected frequency Ei, so we’re actually calculating:
\[\frac{\left(E-O\right)^{2}}{E} \nonumber \]
Since E=50 for all categories in our example, it’s not a very interesting calculation, but let’s do it anyway. The results are shown in another table (Table \(\PageIndex{4}\))!
| Clubs ♣ | Diamonds ♢ | Hearts ♡ | Spades ♠ | |
|---|---|---|---|---|
| Observed Frequency (O) | 35 | 51 | 64 | 50 |
| Expected Frequency (E) | 50 | 50 | 50 | 50 |
| Difference Score (O Minus E) | 15 | -1 | -14 | 0 |
| Difference Score Squared | \(15^2 = 225\) | \((-1)^2 = 1\) |
\((-14)^2 = 196\) |
\(0^2 = 0\) |
| Diff2 divided by Expected | \(\dfrac{225}{50} = 4.50 \) | \(\dfrac{1}{50} = 0.02 \) | \(\dfrac{196}{50} = 3.92 \) | \(\dfrac{0}{50} = 0.00 \) |
In effect, what we’ve got here are four different “error” scores, each one telling us how big a “mistake” the null hypothesis made when we tried to use it to predict our observed frequencies. So, in order to convert this into a useful test statistic, one thing we could do is just add these numbers up. The result is called the Goodness of Fit statistic, conventionally referred to either as \(\chi^2\) r GOF. What's cool about this is that it's easy to calculate if each of the Expected is a different amount of suits, too.
Intuitively, it’s clear that if \(\chi^2\) s small, then the observed data are very close to what the null hypothesis predicted expected values, so we’re going to need a large \(\chi^2\) tatistic in order to reject the null. As we’ve seen from our calculations, in our cards data set we’ve got a value of \(\chi^2\)=8.44 \((4.50 + 0.02 + 3.92 + 0.00 = 8.44)\). So now the question becomes, is this a big enough value to reject the null? The simple answer is that we compare our calculated \(\chi^2\)=8.44 to a critical values in the Critical Values of Chi-Square Table. The longer answer is below.
The Sampling Distribution of the Goodness of Fit Statistic (advanced)
To determine whether or not a particular value of X2 is large enough to justify rejecting the null hypothesis, we’re going to need to figure out what the sampling distribution for \(\chi^2\) would be if the null hypothesis were true. So that’s what I’m going to do in this section. I’ll show you in a fair amount of detail how this sampling distribution is constructed, and then – in the next section – use it to build up a hypothesis test. If you want to cut to the chase and are willing to take it on faith that the sampling distribution is a chi-squared (\(\chi^2\) ) distribution with k−1 degrees of freedom, you can skip the rest of this section. However, if you want to understand why the goodness of fit test works the way it does, read on…
Okay, let’s suppose that the null hypothesis is actually true. If so, then the true probability that an observation falls in the i-th category is Pi – after all, that’s pretty much the definition of our null hypothesis. Let’s think about what this actually means. If you think about it, this is kind of like saying that “nature” makes the decision about whether or not the observation ends up in category by flipping a weighted coin (i.e., one where the probability of getting a head is P). And therefore, we can think of our observed frequency O by imagining that nature flipped N of these coins (one for each observation in the data set)… and exactly Oi of them came up heads. Obviously, this is a pretty weird way to think about the experiment but makes sense if you remember anything about the binomial distribution. Now, if you remember from our discussion of the central limit theorem, the binomial distribution starts to look pretty much identical to the normal distribution, especially when N is large and when the probability isn’t too close to 0 or 1. In other words as long as N×P is large enough – or, to put it another way, when the expected frequency is large enough – the theoretical distribution of O is approximately normal. Better yet, if O is normally distributed, then so is\(\dfrac {(O−E)}{\sqrt{E}}\)… since E is a fixed value, subtracting off E and dividing by \(\sqrt{E}\) changes the mean and standard deviation of the normal distribution; but that’s all it does.
Okay, so now let’s have a look at what our Goodness of Fit statistic actually is. What we’re doing is taking a bunch of things that are normally-distributed, squaring them, and adding them up. Wait. We’ve seen that before too!
When you take a bunch of things that have a standard normal distribution (i.e., mean 0 and standard deviation 1), square them, then add them up, then the resulting quantity has a Chi-Square distribution. So now we know that the null hypothesis predicts that the sampling distribution of the Goodness of Fit statistic is a Chi-Square distribution. Cool. There’s one last detail to talk about, namely the degrees of freedom. What we’re supposed to be looking at is the number of genuinely independent things that are getting added together. And, as I’ll go on to talk about in the next section, even though there’s k things that we’re adding, only k−1 of them are truly independent; and so the degrees of freedom is actually only k−1. If you continue learning about statistics, it will be explained.If you're interested, the next section describes why. However, it's fine to calculate the statistics, even to interpret them, without fully understanding all of these concepts.
Degrees of Freedom
Looking Figure \(\PageIndex{1}\) you can see that if we change the degrees of freedom, then the Chi-Square distribution changes shape quite substantially.
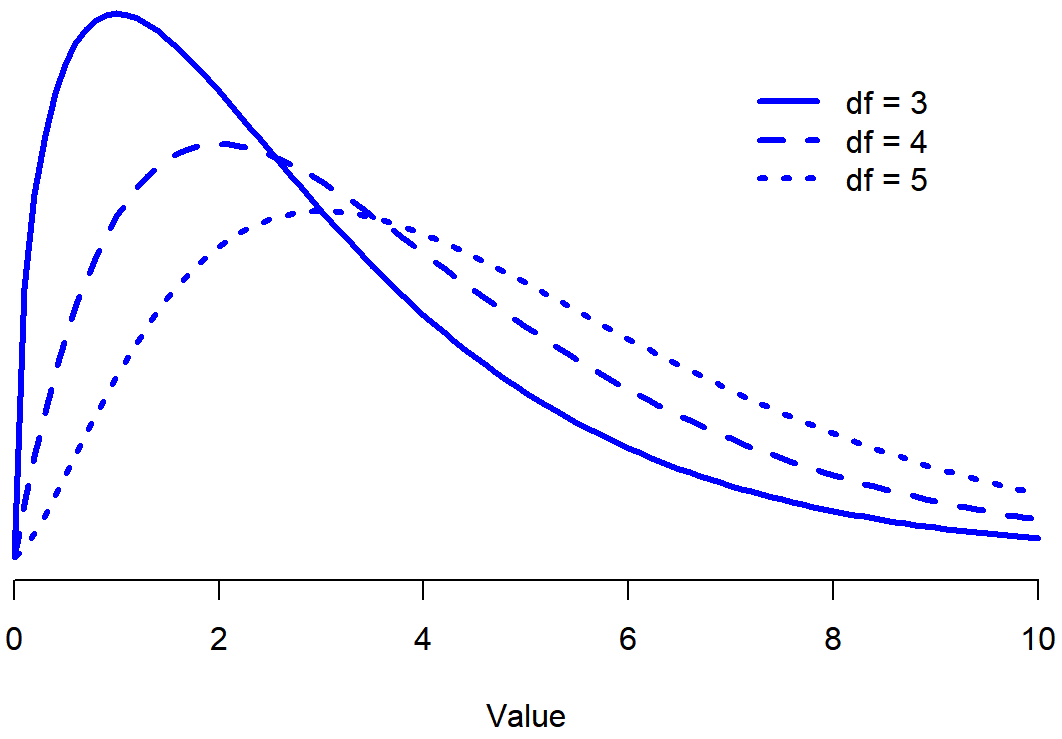
Figure \(\PageIndex{1}\)- Chi-Square Distributions with Different df's(CC-BY-SA- Danielle Navarro from Learning Statistics with R).
But what exactly is it? It’s the number of “normally distributed variables” that are being squared and added together. But, for most people, that’s kind of abstract, and not entirely helpful. What we really need to do is try to understand degrees of freedom in terms of our data. So here goes.
The basic idea behind degrees of freedom is quite simple: you calculate it by counting up the number of distinct “quantities” that are used to describe your data; and then subtracting off all of the “constraints” that those data must satisfy. This is a bit vague, so let’s use our cards data as a concrete example. We describe out data using four numbers, corresponding to the observed frequencies of the four different categories (hearts, clubs, diamonds, spades). These four numbers are the random outcomes of our experiment. But, my experiment actually has a fixed constraint built into it: the sample size. That is, if we know how many people chose hearts, how many chose diamonds and how many chose clubs; then we’d be able to figure out exactly how many chose spades. In other words, although our data are described using four numbers, they only actually correspond to 4−1=3 degrees of freedom. A slightly different way of thinking about it is to notice that there are four probabilities that we’re interested in (again, corresponding to the four different categories), but these probabilities must sum to one, which imposes a constraint. Therefore, the degrees of freedom is 4−1=3. Regardless of whether you want to think about it in terms of the observed frequencies or in terms of the probabilities, the answer is the same.
Testing the Null Hypothesis
The final step in the process of constructing our hypothesis test is to figure out what the rejection region is. That is, what values of \(\chi^2\) would lead is to reject the null hypothesis. As we saw earlier, large values of X2 imply that the null hypothesis has done a poor job of predicting the data from our experiment, whereas small values of X2 imply that it’s actually done pretty well. Therefore, a pretty sensible strategy would be to say there is some critical value, such that if \(\chi^2\) is bigger than the critical value we reject the null; but if \(\chi^2\) is smaller than this value we retain the null. In other words, to use the same language that we've been using! The chi-squared goodness of fit test is always a one-sided test. Right, so all we have to do is figure out what this critical value is. And it’s pretty straightforward. If we want our test to have significance level of α=.05 (that is, we are willing to tolerate a Type I error rate of 5%), then we have to choose our critical value so that there is only a 5% chance that \(\chi^2\) could get to be that big if the null hypothesis is true. That is to say, we want the 95th percentile of the sampling distribution. This is illustrated inFigure \(\PageIndex{2}\).
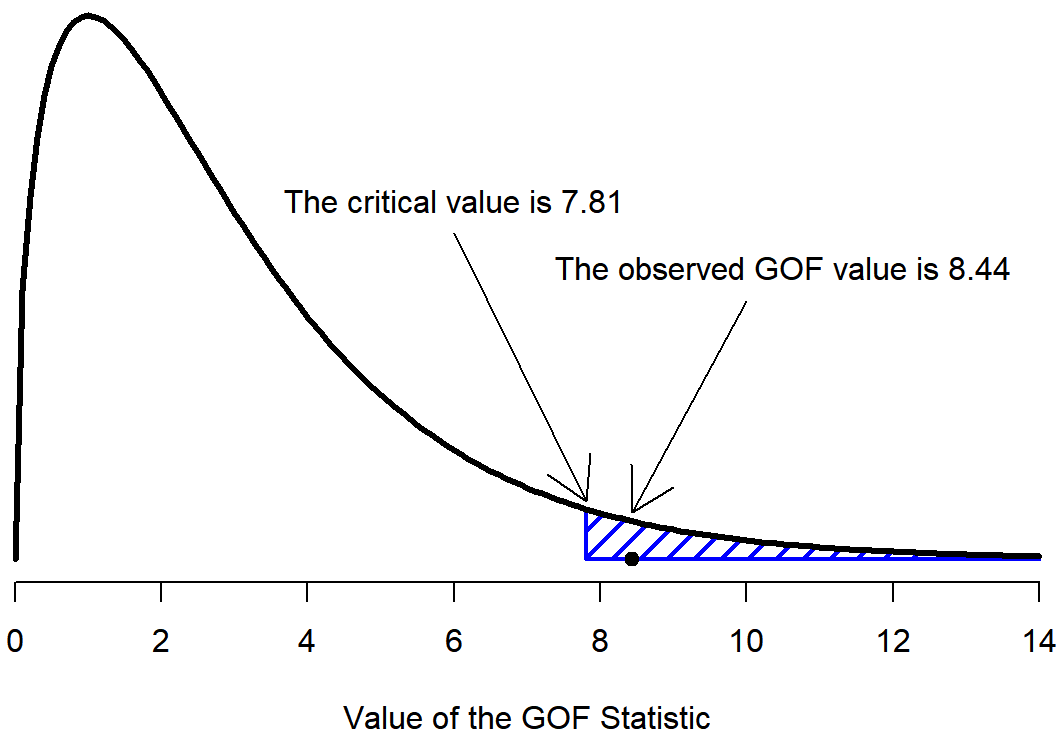
Figure \(\PageIndex{2}\)- Illustration of how the hypothesis testing works for the chi-square goodness of fit test (CC-BY-SA- Danielle Navarro from Learning Statistics with R).
So if our \(\chi^2\) statistic is bigger than 7.81 or so (7.815 from our Critical Values of Chi-Square Table, then we can reject the null hypothesis. Since we actually calculated that before (i.e., \(\chi^2\) = 8.44) we can reject the null. So, in this case we would reject the null hypothesis, since p<.05. And that’s it, basically. You now know “Pearson’s \(\chi^2\) test for the goodness of fit”. Lucky you.
Example \(\PageIndex{1}\)
What do you think that the statistical sentence would look like for this scenario?
Solution
The statistical sentence would be \(\chi^2(3) = 8.44, p<.05\)
Summary
That is a lot of detailed information. If you like to know the "why" behind things, I hope that helped! If you just want the nuts and bolts of how to calculate and then interpret a Chi-Square, I hope that you skimmed this prior section. You will learn how to use the full formula next, and practice calculating and interpreting what it means!
Contributors and Attributions


