Skip to main content
Statistics LibreTexts

16.2.1: Critical Values of Chi-Square Table

  1. Last updated
  2. Save as PDF
  • Page ID
    18948

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

    \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

    \( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

    ( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

    \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

    \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

    \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

    \( \newcommand{\Span}{\mathrm{span}}\)

    \( \newcommand{\id}{\mathrm{id}}\)

    \( \newcommand{\Span}{\mathrm{span}}\)

    \( \newcommand{\kernel}{\mathrm{null}\,}\)

    \( \newcommand{\range}{\mathrm{range}\,}\)

    \( \newcommand{\RealPart}{\mathrm{Re}}\)

    \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

    \( \newcommand{\Argument}{\mathrm{Arg}}\)

    \( \newcommand{\norm}[1]{\| #1 \|}\)

    \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

    \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    \( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

    \( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

    \( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

    \( \newcommand{\vectorC}[1]{\textbf{#1}} \)

    \( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

    \( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

    \( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

    \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

    \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

    \(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)

     A new type of statistical analysis, a new table of critical values!

    Chi-Square Distributions

    As you know, there is a whole family of \(t\)-distributions, each one specified by a parameter called the degrees of freedom (\(df\)). Similarly, all the chi-square distributions form a family, and each of its members is also specified by a its own \(df\). Chi (like "kite," not like "chai" or "Chicago") is a Greek letter denoted by the symbol \(\chi\) and chi-square is often denoted by \(\chi^2\).  It looks like a wiggly X, but is not an X.  Figure \(\PageIndex{1}\) shows several \(\chi\)-square distributions for different degrees of freedom. 

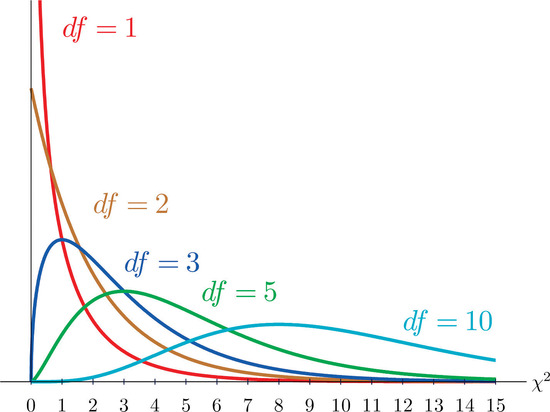
    Many different line graphs showing Chi-Square distributions with different Degrees of Freedom (df).
    Figure \(\PageIndex{1}\): Many \(\chi\) Distributions (CC-BY-NC-SA Shafer & Zhang)

    Like all tables of critical values, this one provides the value in which you should reject the null hypothesis if your calculated value is bigger than the critical value i the table.  For chi-square, the null hypothesis is that there is no pattern of relationship, but the process of Null Hypothesis Signficance Testing is the same as we've been learning. 

    Note

    Critical < Calculated == Reject null == There is a pattern of relationship. == p<.05

    Critical > Calculated == Retain null ==  There is no pattern of relationship. == p>.05

    Illustrated in Figure \(\PageIndex{2}\), the value of the chi-square that cuts off a right tail of area \(c\) is denoted \(\chi_c^2\) and is called a critical value (Figure \(\PageIndex{2}\)).

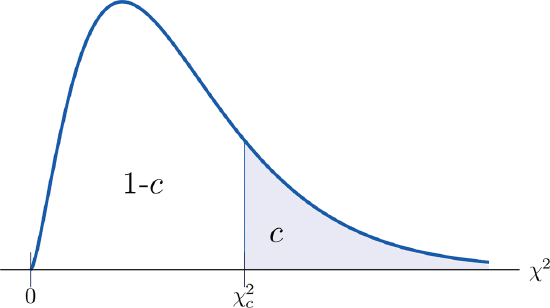
    Basic Chi-Square distribution which is a line graph that leans a little to the left. There's a line marking the critical region, with everything to the right of the line shaded.
    Figure \(\PageIndex{2}\): \(\chi_c^2\) Illustration of Critical Values of Chi-Square. (CC-BY-NC-SA Shafer & Zhang)

    Table of Critical Values for \(\chi_c^2\)

    Table \(\PageIndex{1}\) below gives values of \(\chi_c^2\) for various values of \(c\) and under several chi-square distributions with various degrees of freedom.

    Table \(\PageIndex{1}\)- Critical Values on the Right Side of the Distribution of Chi-Square
    df p = 0.10 p = 0.05 p = 0.01
    1 2.706 3.841 6.635
    2 4.605 5.991 9.210
    3 6.251 7.815 11.345
    4 7.779 9.488 13.277
    5 9.236 11.070 15.086
    6 10.645 12.592 16.812
    7 12.017 14.067 18.475
    8 13.362 15.507 20.090
    9 14.684 16.919 21.666
    10 15.987 18.307 23.209
    11 17.275 19.675 24.725
    12 18.549 21.026 26.217
    13 19.812 22.362 27.688
    14 21.064 23.685 29.141
    15 22.307 24.996 30.578
    16 23.542 26.296 32.000
    17 24.769 27.587 33.409
    18 25.989 28.869 34.805
    19 27.204 30.144 36.191
    20 28.412 31.410 37.566
    100 118.498 124.342 135.807

    Degrees of Freedom

    Like with the t-test and ANOVA, the degrees of freedom are based on which kind of analysis you are conducting.

    • \(\chi_{GoF}^2\) Goodness of Fit:  \(k-1\)
      • k is the number of categories.
    • \(\chi_{ToI}^2\) Test of Independence: \((R-1)\times(C-1) \)
      • R is the number of rows
      • C is the number of columns
    • Kruskal-Wallis Test:  \(k-1 \)
      • k is the number of groups

    Contributor

     

    This page titled 16.2.1: Critical Values of Chi-Square Table is shared under a CC BY-NC-SA license and was authored, remixed, and/or curated by Michelle Oja.