11.1: Chi-Square Tests for Independence
- Page ID
- 513
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)- To understand what chi-square distributions are.
- To understand how to use a chi-square test to judge whether two factors are independent.
Chi-Square Distributions
As you know, there is a whole family of \(t\)-distributions, each one specified by a parameter called the degrees of freedom, denoted \(df\). Similarly, all the chi-square distributions form a family, and each of its members is also specified by a parameter \(df\), the number of degrees of freedom. Chi is a Greek letter denoted by the symbol \(\chi\) and chi-square is often denoted by \(\chi^2\).
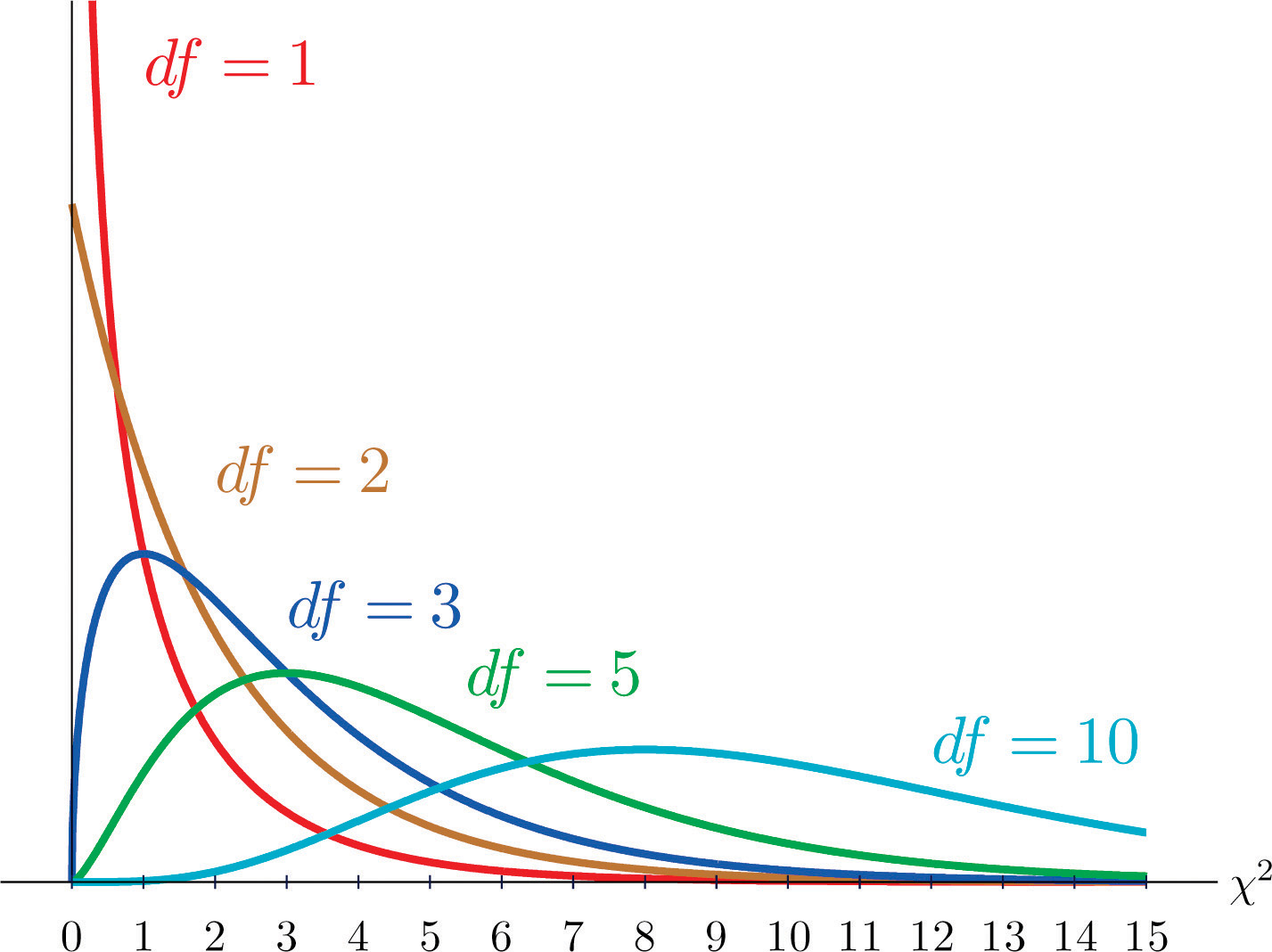
Figure \(\PageIndex{1}\) shows several \(\chi\)-square distributions for different degrees of freedom. A chi-square random variable is a random variable that assumes only positive values and follows a \(\chi\)-square distribution.
The value of the chi-square random variable \(\chi^2\) with \(df=k\) that cuts off a right tail of area \(c\) is denoted \(\chi_c^2\) and is called a critical value (Figure \(\PageIndex{2}\)).
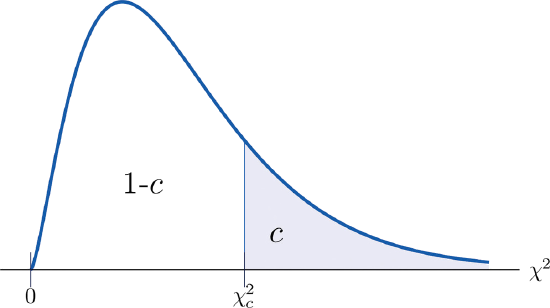
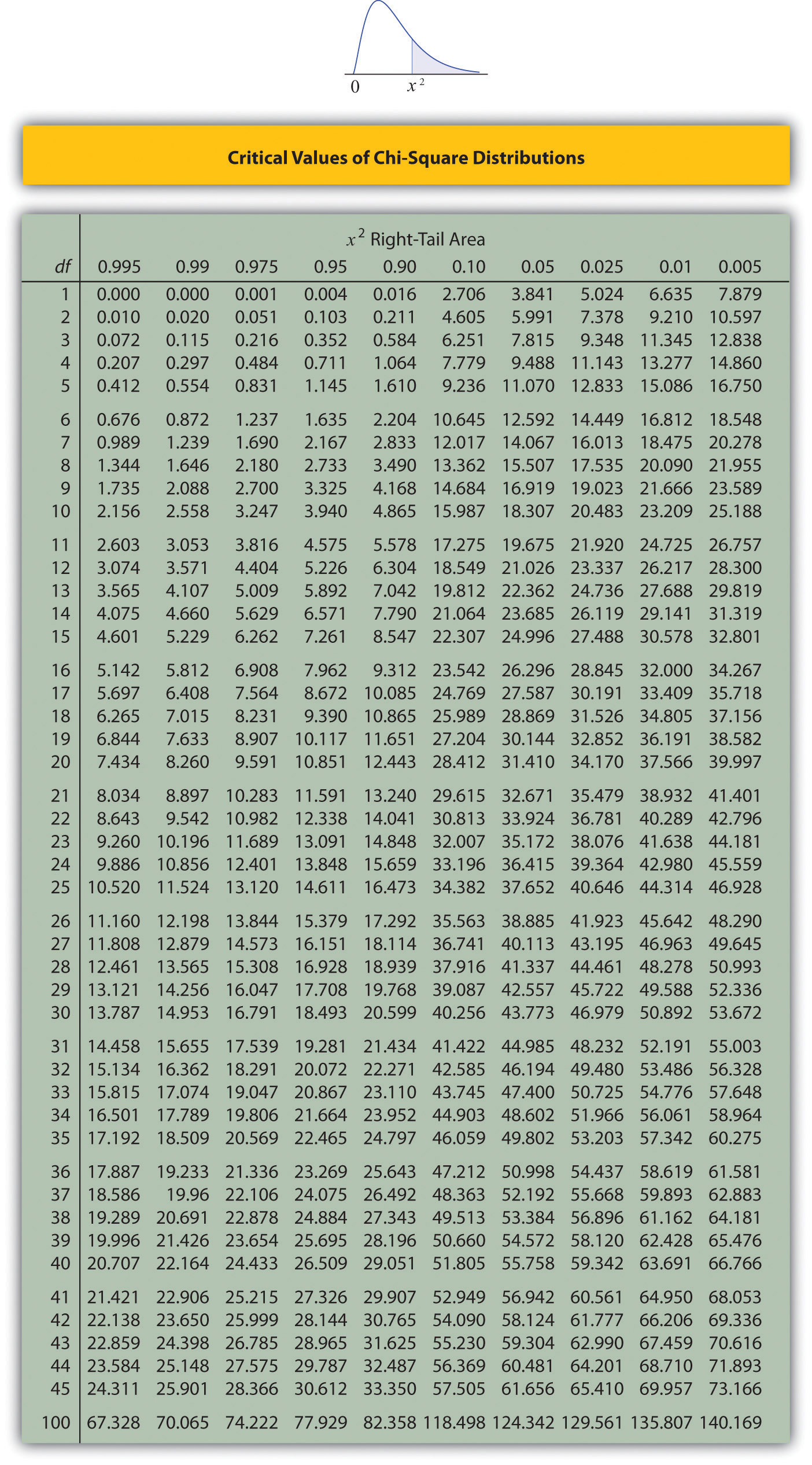
Figure \(\PageIndex{3}\) below gives values of \(\chi_c^2\) for various values of \(c\) and under several chi-square distributions with various degrees of freedom.
Tests for Independence
Hypotheses tests encountered earlier in the book had to do with how the numerical values of two population parameters compared. In this subsection we will investigate hypotheses that have to do with whether or not two random variables take their values independently, or whether the value of one has a relation to the value of the other. Thus the hypotheses will be expressed in words, not mathematical symbols. We build the discussion around the following example.
There is a theory that the gender of a baby in the womb is related to the baby’s heart rate: baby girls tend to have higher heart rates. Suppose we wish to test this theory. We examine the heart rate records of \(40\) babies taken during their mothers’ last prenatal checkups before delivery, and to each of these \(40\) randomly selected records we compute the values of two random measures: 1) gender and 2) heart rate. In this context these two random measures are often called factors. Since the burden of proof is that heart rate and gender are related, not that they are unrelated, the problem of testing the theory on baby gender and heart rate can be formulated as a test of the following hypotheses:
\[H_0: \text{Baby gender and baby heart rate are independent}\\ vs. \\ H_a: \text{Baby gender and baby heart rate are not independent} \nonumber \]
The factor gender has two natural categories or levels: boy and girl. We divide the second factor, heart rate, into two levels, low and high, by choosing some heart rate, say \(145\) beats per minute, as the cutoff between them. A heart rate below \(145\) beats per minute will be considered low and \(145\) and above considered high. The \(40\) records give rise to a \(2\times 2\) contingency table. By adjoining row totals, column totals, and a grand total we obtain the table shown as Table \(\PageIndex{1}\). The four entries in boldface type are counts of observations from the sample of \(n = 40\). There were \(11\) girls with low heart rate, \(17\) boys with low heart rate, and so on. They form the core of the expanded table.
| Heart Rate | ||||
|---|---|---|---|---|
| \(\text{Low}\) | \(\text{High}\) | \(\text{Row Total}\) | ||
| \(\text{Gender}\) | \(\text{Girl}\) | \(11\) | \(7\) | \(18\) |
| \(\text{Boy}\) | \(17\) | \(5\) | \(22\) | |
| \(\text{Column Total}\) | \(28\) | \(12\) | \(\text{Total}=40\) | |
In analogy with the fact that the probability of independent events is the product of the probabilities of each event, if heart rate and gender were independent then we would expect the number in each core cell to be close to the product of the row total \(R\) and column total \(C\) of the row and column containing it, divided by the sample size \(n\). Denoting such an expected number of observations \(E\), these four expected values are:
- 1st row and 1st column: \(E=(R\times C)/n = 18\times 28 /40 = 12.6\)
- 1st row and 2nd column: \(E=(R\times C)/n = 18\times 12 /40 = 5.4\)
- 2nd row and 1st column: \(E=(R\times C)/n = 22\times 28 /40 = 15.4\)
- 2nd row and 2nd column: \(E=(R\times C)/n = 22\times 12 /40 = 6.6\)
We update Table \(\PageIndex{1}\) by placing each expected value in its corresponding core cell, right under the observed value in the cell. This gives the updated table Table \(\PageIndex{2}\).
| \(\text{Heart Rate}\) | ||||
|---|---|---|---|---|
| \(\text{Low}\) | \(\text{High}\) | \(\text{Row Total}\) | ||
| \(\text{Gender}\) | \(\text{Girl}\) |
\(O=11\) \(E=12.6\) |
\(O=7\) \(E=5.4\) |
\(R = 18\) |
| \(\text{Boy}\) |
\(O=17\) \(E=15.4\) |
\(O=5\) \(E=6.6\) |
\(R = 22\) | |
| \(\text{Column Total}\) | \(C = 28\) | \(C = 12\) | \(n = 40\) | |
A measure of how much the data deviate from what we would expect to see if the factors really were independent is the sum of the squares of the difference of the numbers in each core cell, or, standardizing by dividing each square by the expected number in the cell, the sum \(\sum (O-E)^2 / E\). We would reject the null hypothesis that the factors are independent only if this number is large, so the test is right-tailed. In this example the random variable \(\sum (O-E)^2 / E\) has the chi-square distribution with one degree of freedom. If we had decided at the outset to test at the \(10\%\) level of significance, the critical value defining the rejection region would be, reading from Figure \(\PageIndex{3}\), \(\chi _{\alpha }^{2}=\chi _{0.10 }^{2}=2.706\), so that the rejection region would be the interval \([2.706,\infty )\). When we compute the value of the standardized test statistic we obtain
\[\sum \frac{(O-E)^2}{E}=\frac{(11-12.6)^2}{12.6}+\frac{(7-5.4)^2}{5.4}+\frac{(17-15.4)^2}{15.4}+\frac{(5-6.6)^2}{6.6}=1.231 \nonumber \]
Since \(1.231 < 2.706\), the decision is not to reject \(H_0\). See Figure \(\PageIndex{4}\). The data do not provide sufficient evidence, at the \(10\%\) level of significance, to conclude that heart rate and gender are related.
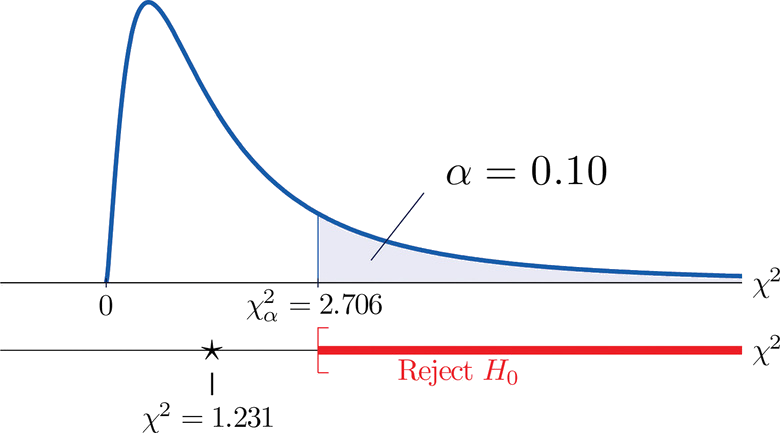
Figure \(\PageIndex{4}\): Baby Gender Prediction
H0vs. Ha::Baby gender and baby heart rate are independentBaby gender and baby heart rate are not independentH0vs. Ha::Baby gender and baby heart rate are independentBaby gender and baby heart rate are not independent
With this specific example in mind, now turn to the general situation. In the general setting of testing the independence of two factors, call them Factor \(1\) and Factor \(2\), the hypotheses to be tested are
\[H_0: \text{The two factors are independent}\\ vs. \\ H_a: \text{The two factors are not independent} \nonumber \]
As in the example each factor is divided into a number of categories or levels. These could arise naturally, as in the boy-girl division of gender, or somewhat arbitrarily, as in the high-low division of heart rate. Suppose Factor \(1\) has \(I\) levels and Factor \(2\) has \(J\) levels. Then the information from a random sample gives rise to a general \(I\times J\) contingency table, which with row totals, column totals, and a grand total would appear as shown in Table \(\PageIndex{3}\). Each cell may be labeled by a pair of indices \((i,j)\). \(O_{ij}\) stands for the observed count of observations in the cell in row \(i\) and column \(j\), \(R_i\) for the \(i^{th}\) row total and \(C_j\) for the \(j^{th}\) column total. To simplify the notation we will drop the indices so Table \(\PageIndex{3}\) becomes Table \(\PageIndex{4}\). Nevertheless it is important to keep in mind that the \(Os\), the \(Rs\) and the \(Cs\), though denoted by the same symbols, are in fact different numbers.
| \(\text{Factor 2 Levels}\) | |||||||
|---|---|---|---|---|---|---|---|
| \(1\) | ⋅ ⋅ ⋅ | \(j\) | ⋅ ⋅ ⋅ | \(J\) | \(\text{Row Total}\) | ||
| \(\text{Factor 1 Levels}\) | \(1\) | \(O_{11}\) | ⋅ ⋅ ⋅ | \(O_{1j}\) | ⋅ ⋅ ⋅ | \(O_{1J}\) | \(R_1\) |
| ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | |
| \(i\) | \(O_{i1}\) | ⋅ ⋅ ⋅ | \(O_{ij}\) | ⋅ ⋅ ⋅ | \(O_{iJ}\) | \(R_i\) | |
| ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | |
| \(I\) | \(O_{I1}\) | ⋅ ⋅ ⋅ | \(O_{Ij}\) | ⋅ ⋅ ⋅ | \(O_{IJ}\) | \(R_I\) | |
| \(\text{Column Total}\) | \(C_1\) | ⋅ ⋅ ⋅ | \(C_j\) | ⋅ ⋅ ⋅ | \(C_J\) | \(n\) | |
| \(\text{Factor 2 Levels}\) | |||||||
|---|---|---|---|---|---|---|---|
| \(1\) | ⋅ ⋅ ⋅ | \(j\) | ⋅ ⋅ ⋅ | \(J\) | \(\text{Row Total}\) | ||
|
\(\text{Factor 1 Levels}\) |
\(1\) | \(O\) | ⋅ ⋅ ⋅ | \(O\) | ⋅ ⋅ ⋅ | \(O\) | \(R\) |
| ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | |
| \(i\) | \(O\) | ⋅ ⋅ ⋅ | \(O\) | ⋅ ⋅ ⋅ | \(O\) | \(R\) | |
| ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | |
| \(I\) | \(O\) | ⋅ ⋅ ⋅ | \(O\) | ⋅ ⋅ ⋅ | \(O\) | \(R\) | |
| \(\text{Column Total}\) | \(C\) | ⋅ ⋅ ⋅ | \(C\) | ⋅ ⋅ ⋅ | \(C\) | \(n\) | |
As in the example, for each core cell in the table we compute what would be the expected number \(E\) of observations if the two factors were independent. \(E\) is computed for each core cell (each cell with an \(O\) in it) of Table \(\PageIndex{4}\) by the rule applied in the example:
\[E=R×Cn \nonumber \]
where \(R\) is the row total and \(C\) is the column total corresponding to the cell, and \(n\) is the sample size
| \(\text{Factor 2 Levels}\) | |||||||
|---|---|---|---|---|---|---|---|
| \(1\) | ⋅ ⋅ ⋅ | \(j\) | ⋅ ⋅ ⋅ | \(J\) | \(\text{Row Total}\) | ||
|
\(\text{Factor 1 Levels}\) |
\(1\) |
\(O\) \(E\) |
⋅ ⋅ ⋅ |
\(O\) \(E\) |
⋅ ⋅ ⋅ |
\(O\) \(E\) |
\(R\) |
| ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | |
| \(i\) |
\(O\) \(E\) |
⋅ ⋅ ⋅ |
\(O\) \(E\) |
⋅ ⋅ ⋅ |
\(O\) \(E\) |
\(R\) |
|
| ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | |
| \(I\) |
\(O\) \(E\) |
⋅ ⋅ ⋅ |
\(O\) \(E\) |
⋅ ⋅ ⋅ |
\(O\) \(E\) |
\(R\) |
|
| \(\text{Column Total}\) | \(C\) | ⋅ ⋅ ⋅ | \(C\) | ⋅ ⋅ ⋅ | \(C\) | \(n\) | |
Here is the test statistic for the general hypothesis based on Table \(\PageIndex{5}\), together with the conditions that it follow a chi-square distribution.
\[\chi^2=\sum (O−E)^2E \nonumber \]
where the sum is over all core cells of the table.
If
- the two study factors are independent, and
- the observed count \(O\) of each cell in Table \(\PageIndex{5}\) is at least \(5\),
then \(\chi ^2\) approximately follows a chi-square distribution with \(df=(I-1)\times (J-1)\) degrees of freedom.
The same five-step procedures, either the critical value approach or the \(p\)-value approach, that were introduced in Section 8.1 and Section 8.3 are used to perform the test, which is always right-tailed.
A researcher wishes to investigate whether students’ scores on a college entrance examination (\(CEE\)) have any indicative power for future college performance as measured by \(GPA\). In other words, he wishes to investigate whether the factors \(CEE\) and \(GPA\) are independent or not. He randomly selects \(n = 100\) students in a college and notes each student’s score on the entrance examination and his grade point average at the end of the sophomore year. He divides entrance exam scores into two levels and grade point averages into three levels. Sorting the data according to these divisions, he forms the contingency table shown as Table \(\PageIndex{6}\), in which the row and column totals have already been computed.
| \(GPA\) | |||||
|---|---|---|---|---|---|
| \(<2.7\) | \(2.7\; \; \text{to}\; \; 3.2\) | \(>3.2\) | \(\text{Row Total}\) | ||
| \(CEE\) | \(<1800\) | \(35\) | \(12\) | \(5\) | \(52\) |
| \(\geq 1800\) | \(6\) | \(24\) | \(18\) | \(48\) | |
| \(\text{Column Total}\) | \(41\) | \(36\) | \(23\) | \(\text{Total}=100\) | |
Test, at the \(1\%\) level of significance, whether these data provide sufficient evidence to conclude that \(CEE\) scores indicate future performance levels of incoming college freshmen as measured by \(GPA\).
Solution
We perform the test using the critical value approach, following the usual five-step method outlined at the end of Section 8.1.
- Step 1. The hypotheses are \[H_0:\text{CEE and GPA are independent factors}\\ vs.\\ H_a:\text{CEE and GPA are not independent factors} \nonumber \]
- Step 2. The distribution is chi-square.
- Step 3. To compute the value of the test statistic we must first computed the expected number for each of the six core cells (the ones whose entries are boldface):
- 1st row and 1st column: \(E=(R\times C)/n=41\times 52/100=21.32\)
- 1st row and 2nd column: \(E=(R\times C)/n=36\times 52/100=18.72\)
- 1st row and 3rd column: \(E=(R\times C)/n=23\times 52/100=11.96\)
- 2nd row and 1st column: \(E=(R\times C)/n=41\times 48/100=19.68\)
- 2nd row and 2nd column: \(E=(R\times C)/n=36\times 48/100=17.28\)
- 2nd row and 3rd column: \(E=(R\times C)/n=23\times 48/100=11.04\)
Table \(\PageIndex{6}\) is updated to Table \(\PageIndex{6}\).
| \(GPA\) | |||||
|---|---|---|---|---|---|
| \(<2.7\) | \(2.7\; \; \text{to}\; \; 3.2\) | \(>3.2\) | \(\text{Row Total}\) | ||
| \(CEE\) | \(<1800\) |
\(O=35\) \(E=21.32\) |
\(O=12\) \(E=18.72\) |
\(O=5\) \(E=11.96\) |
\(R = 52\) |
| \(\geq 1800\) |
\(O=6\) \(E=19.68\) |
\(O=24\) \(E=17.28\) |
\(O=18\) \(E=11.04\) |
\(R = 48\) | |
| \(\text{Column Total}\) | \(C = 41\) | \(C = 36\) | \(C = 23\) | \(n = 100\) | |
The test statistic is
\[\begin{align*} \chi^2 &= \sum \frac{(O-E)^2}{E}\\ &= \frac{(35-21.32)^2}{21.32}+\frac{(12-18.72)^2}{18.72}+\frac{(5-11.96)^2}{11.96}+\frac{(6-19.68)^2}{19.68}+\frac{(24-17.28)^2}{17.28}+\frac{(18-11.04)^2}{11.04}\\ &= 31.75 \end{align*} \nonumber \]
- Step 4. Since the \(CEE\) factor has two levels and the \(GPA\) factor has three, \(I = 2\) and \(J = 3\). Thus the test statistic follows the chi-square distribution with \(df=(2-1)\times (3-1)=2\) degrees of freedom.
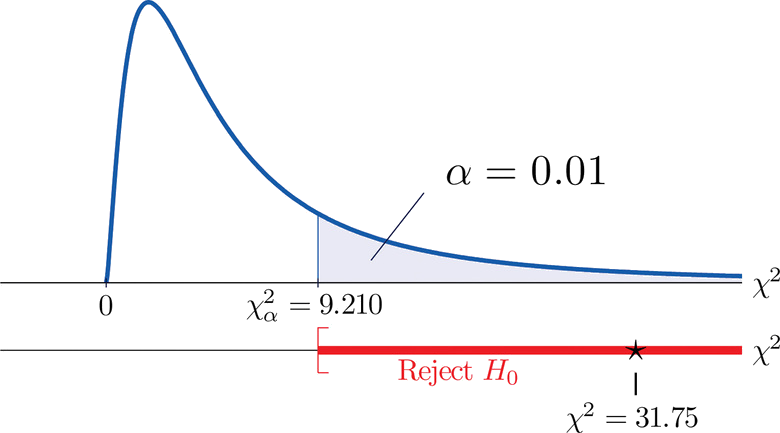
Since the test is right-tailed, the critical value is \(\chi _{0.01}^{2}\). Reading from Figure 7.1.6 "Critical Values of Chi-Square Distributions", \(\chi _{0.01}^{2}=9.210\), so the rejection region is \([9.210,\infty )\).
- Step 5. Since \(31.75 > 9.21\) the decision is to reject the null hypothesis. See Figure \(\PageIndex{5}\). The data provide sufficient evidence, at the \(1\%\) level of significance, to conclude that \(CEE\) score and \(GPA\) are not independent: the entrance exam score has predictive power.
- Critical values of a chi-square distribution with degrees of freedom df are found in Figure 7.1.6.
- A chi-square test can be used to evaluate the hypothesis that two random variables or factors are independent.


