1.6: Exponential and Logarithmic Functions
- Page ID
- 25917
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)- Identify the form of an exponential function.
- Explain the difference between the graphs of \(x^{b}\) and \(b^{x}\).
- Recognize the significance of the number \(e\).
- Identify the form of a logarithmic function.
- Explain the relationship between exponential and logarithmic functions.
- Describe how to calculate a logarithm to a different base.
- Identify the hyperbolic functions, their graphs, and basic identities.
In this section we examine exponential and logarithmic functions. We use the properties of these functions to solve equations involving exponential or logarithmic terms, and we study the meaning and importance of the number \(e\). We also define hyperbolic and inverse hyperbolic functions, which involve combinations of exponential and logarithmic functions. (Note that we present alternative definitions of exponential and logarithmic functions in the chapter Applications of Integrations, and prove that the functions have the same properties with either definition.)
Exponential Functions
Exponential functions arise in many applications. One common example is population growth. For example, if a population starts with \(P_0\) individuals and then grows at an annual rate of \(2\%\), its population after 1 year is
\[P(1)=P_0+0.02P_0=P_0(1+0.02)=P_0(1.02).\nonumber \]
Its population after 2 years is
\[P(2)=P(1)+0.02P(1)=P(1)(1.02)=P_0(1.02)^2.\nonumber \]
In general, its population after \(t\) years is
\[P(t)=P_0(1.02)^t,\nonumber \]
which is an exponential function. More generally, any function of the form \(f(x)=b^x\), where \(b>0\), \(b≠1\), is an exponential function with base \(b\) and exponent \(x.\) Exponential functions have constant bases and variable exponents. Note that a function of the form \(f(x)=x^b\) for some constant \(b\) is not an exponential function but a power function.
To see the difference between an exponential function and a power function, we compare the functions \(y=x^2\) and \(y=2^x\). In Table \(\PageIndex{1}\), we see that both \(2^x\) and \(x^2\) approach infinity as \(x→∞\). Eventually, however, \(2^x\) becomes larger than \(x^2\) and grows more rapidly as \(x→∞\). In the opposite direction, as \(x→−∞\), \(x^2→∞\), whereas \(2^x→0\). The line \(y=0\) is a horizontal asymptote for \(y=2^x\).
| \(x\) | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|---|---|---|---|
| \(x^2\) | 9 | 4 | 1 | 0 | 1 | 4 | 9 | 16 | 25 | 36 |
| \(2^x\) | 1/8 | 1/4 | 1/2 | 1 | 2 | 4 | 8 | 16 | 32 | 64 |
In Figure \(\PageIndex{1}\), we graph both \(y=x^2\) and \(y=2^x\) to show how the graphs differ.
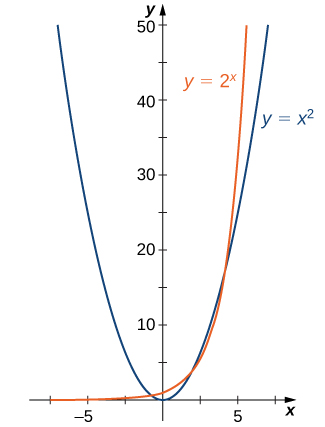 Figure \(\PageIndex{1}\): Both \(2^x\) and \(x^2\) approach infinity as \(x→∞\), but \(2^x\) grows more rapidly than \(x^2\). As \(x→−∞\), \(x^2→∞\), whereas \(2^x→0\).
Figure \(\PageIndex{1}\): Both \(2^x\) and \(x^2\) approach infinity as \(x→∞\), but \(2^x\) grows more rapidly than \(x^2\). As \(x→−∞\), \(x^2→∞\), whereas \(2^x→0\).
Evaluating Exponential Functions
Recall the properties of exponents: If \(x\) is a positive integer, then we define \(b^x=b⋅b⋯b\) (with \(x\) factors of \(b\)). If \(x\) is a negative integer, then \(x=−y\) for some positive integer \(y\), and we define \(b^x=b^{−y}=1/b^y\). Also, \(b^0\) is defined to be \(1\). If \(x\) is a rational number, then \(x=p/q\), where \(p\) and \(q\) are integers and \(b^x=b^{p/q}=\sqrt[q]{b^p}\). For example, \(9^{3/2}=\sqrt{9^3}=\left(\sqrt{9}\right)^3=27\). However, how is \(b^x\) defined if \(x\) is an irrational number? For example, what do we mean by \(2^{\sqrt{2}}\)? This is too complex a question for us to answer fully right now; however, we can make an approximation.
| \(x\) | 1.4 | 1.41 | 1.414 | 1.4142 | 1.41421 | 1.414213 |
|---|---|---|---|---|---|---|
| \(2^x\) | 2.639 | 2.65737 | 2.66475 | 2.665119 | 2.665138 | 2.665143 |
In Table \(\PageIndex{2}\), we list some rational numbers approaching \(\sqrt{2}\), and the values of \(2^x\) for each rational number \(x\) are presented as well. We claim that if we choose rational numbers \(x\) getting closer and closer to \(\sqrt{2}\), the values of \(2^x\) get closer and closer to some number \(L\). We define that number \(L\) to be \(2^{\sqrt{2}}\).
Suppose a particular population of bacteria is known to double in size every \(4\) hours. If a culture starts with \(1000\) bacteria, the number of bacteria after \(4\) hours is \(n(4)=1000⋅2\). The number of bacteria after \(8\) hours is \(n(8)=n(4)⋅2=1000⋅2^2\). In general, the number of bacteria after \(4m\) hours is \(n(4m)=1000⋅2^m\). Letting \(t=4m\), we see that the number of bacteria after t hours is \(n(t)=1000⋅2^{t/4}\). Find the number of bacteria after \(6\) hours, \(10\) hours, and \(24\) hours.
Solution
The number of bacteria after 6 hours is given by
\[n(6)=1000⋅2^{6/4}≈2828\, \text{bacteria}. \nonumber \]
The number of bacteria after \(10\) hours is given by
\[n(10)=1000⋅2^{10/4}≈5657\, \text{bacteria}. \nonumber \]
The number of bacteria after \(24\) hours is given by \(n(24)=1000⋅2^6=64,000\) bacteria.
Given the exponential function \(f(x)=100⋅3^{x/2}\), evaluate \(f(4)\) and \(f(10)\).
- Answer
-
\(f(4)=900\)
\(f(10)=24,300\).
Graphing Exponential Functions
For any base \(b>0\), \(b≠1\), the exponential function \(f(x)=b^x\) is defined for all real numbers \(x\) and \(b^x>0\). Therefore, the domain of \(f(x)=b^x\) is \((−∞,∞)\) and the range is \((0,∞)\). To graph \(b^x\), we note that for \(b>1\), \(b^x\) is increasing on \((−∞,∞)\) and \(b^x→∞\) as \(x→∞\), whereas \(b^x→0\) as \(x→−∞\). On the other hand, if \(0<b<1\), \(f(x)=b^x\) is decreasing on \((−∞,∞)\) and \(b^x→0\) as \(x→∞\) whereas \(b^x→∞\) as \(x→−∞\) (Figure \(\PageIndex{2}\)).
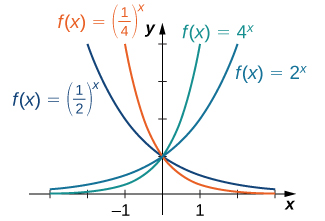 Figure \(\PageIndex{2}\): If \(b>1\), then \(b^x\) is increasing on \((−∞,∞)\). If \(0<b<1\), then \(b^x\) is decreasing on \((−∞,∞)\).
Figure \(\PageIndex{2}\): If \(b>1\), then \(b^x\) is increasing on \((−∞,∞)\). If \(0<b<1\), then \(b^x\) is decreasing on \((−∞,∞)\).
Note that exponential functions satisfy the general laws of exponents. To remind you of these laws, we state them as rules.
For any constants \(a>0\), \(b>0\), and for all \(x\) and \(y,\)
- \[b^x⋅b^y=b^{x+y} \nonumber \]
- \[\dfrac{b^x}{b^y}=b^{x−y} \nonumber \]
- \[(b^x)^y=b^{xy} \nonumber \]
- \[(ab)^x=a^xb^x \nonumber \]
- \[\dfrac{a^x}{b^x}=\left(\dfrac{a}{b}\right)^x \nonumber \]
Use the laws of exponents to simplify each of the following expressions.
- \(\dfrac{(2x^{2/3})^3}{(4x^{−1/3})^2}\)
- \(\dfrac{(x^3y^{−1})^2}{(xy^2)^{−2}}\)
Soution
a. We can simplify as follows:
\[\dfrac{(2x^{2/3})^3}{(4x^{−1/3})^2}=\dfrac{2^3(x^{2/3})^3}{4^2(x^{−1/3})^2}= \dfrac{8x^2}{16x^{−2/3}} =\dfrac{x^2x^{2/3}}{2}=\dfrac{x^{8/3}}{2}. \nonumber \]
b. We can simplify as follows:
\[\dfrac{(x^3y^{−1})^2}{(xy^2)^{−2}}=\dfrac{(x^3)^2(y^{−1})^2}{x^{−2}(y^2)^{−2}}=\dfrac{x^6y^{−2}}{x^{−2}y^{−4}} =x^6x^2y^{−2}y^4=x^8y^2. \nonumber \]
Use the laws of exponents to simplify \(\dfrac{6x^{−3}y^2}{12x^{−4}y^5}\).
- Hint
-
\(x^a/x^b=x^{a-b}\)
- Answer
-
\(x/(2y^3)\)
The Number e
A special type of exponential function appears frequently in real-world applications. To describe it, consider the following example of exponential growth, which arises from compounding interest in a savings account. Suppose a person invests \(P\) dollars in a savings account with an annual interest rate \(r\), compounded annually. The amount of money after 1 year is
\(A(1)=P+rP=P(1+r)\).
The amount of money after \(2\) years is
\(A(2)=A(1)+rA(1)=P(1+r)+rP(1+r)=P(1+r)^2\).
More generally, the amount after \(t\) years is
\(A(t)=P(1+r)^t\).
If the money is compounded 2 times per year, the amount of money after half a year is
\(A\left(\dfrac{1}{2}\right)=P+\left(\dfrac{r}{2}\right)P=P\left(1+\left(\dfrac{r}{2}\right)\right)\).
The amount of money after \(1\) year is
\(A(1)=A\left(\dfrac{1}{2}\right)+\left(\dfrac{r}{2}\right)A \left(\dfrac{1}{2}\right)=P\left(1+\dfrac{r}{2}\right)+\dfrac{r}{2}\left(\left(P(1+\dfrac{r}{2}\right)\right)=P\left(1+\dfrac{r}{2}\right)^2.\)
After \(t\) years, the amount of money in the account is
\(A(t)=P\left(1+\dfrac{r}{2}\right)^{2t}\).
More generally, if the money is compounded \(n\) times per year, the amount of money in the account after \(t\) years is given by the function
\(A(t)=P\left(1+\dfrac{r}{n}\right)^{nt}.\)
What happens as \(n→∞?\) To answer this question, we let \(m=n/r\) and write
\(\left(1+\dfrac{r}{n}\right)^{nt}=\left(1+\dfrac{1}{m}\right)^{mrt},\)
and examine the behavior of \((1+1/m)^m\) as \(m→∞\), using a table of values (Table \(\PageIndex{3}\)).
| \(m\) | 10 | 100 | 1000 | 10,000 | 100,000 | 1,000,000 |
|---|---|---|---|---|---|---|
| \(\left(1+\dfrac{1}{m}\right)^m\) | 2.5937 | 2.7048 | 2.71692 | 2.71815 | 2.718268 | 2.718280 |
Looking at this table, it appears that \((1+1/m)^m\) is approaching a number between \(2.7\) and \(2.8\) as \(m→∞\). In fact, \((1+1/m)^m\) does approach some number as \(m→∞\). We call this number \(e\). To six decimal places of accuracy,
\[e≈2.718282. \nonumber \]
The letter \(e\) was first used to represent this number by the Swiss mathematician Leonhard Euler during the 1720s. Although Euler did not discover the number, he showed many important connections between \(e\) and logarithmic functions. We still use the notation \(e\) today to honor Euler’s work because it appears in many areas of mathematics and because we can use it in many practical applications.
Returning to our savings account example, we can conclude that if a person puts \(P\) dollars in an account at an annual interest rate \(r\), compounded continuously, then \(A(t)=Pe^{rt}\). This function may be familiar. Since functions involving base \(e\) arise often in applications, we call the function \(f(x)=e^x\) the natural exponential function. Not only is this function interesting because of the definition of the number \(e\), but also, as discussed next, its graph has an important property.
Since \(e>1\), we know \(f(x) = e^x\) is increasing on \((−∞,∞)\). In Figure \(\PageIndex{3}\), we show a graph of \(f(x)=e^x\) along with a tangent line to the graph of \(f\) at \(x=0\). We give a precise definition of tangent line in the next chapter; but, informally, we say a tangent line to a graph of \(f\) at \(x=a\) is a line that passes through the point \((a,f(a))\) and has the same “slope” as \(f\) at that point . The function \(f(x)=e^x\) is the only exponential function \(b^x\) with tangent line at \(x=0\) that has a slope of \(1.\) As we see later in the text, having this property makes the natural exponential function the most simple exponential function to use in many instances.
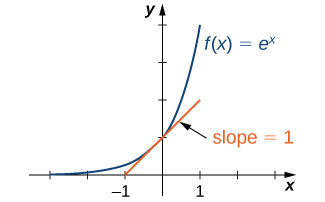 Figure \(\PageIndex{3}\): The graph of \(f(x)=e^x\) has a tangent line with slope \(1\) at \(x=0\).
Figure \(\PageIndex{3}\): The graph of \(f(x)=e^x\) has a tangent line with slope \(1\) at \(x=0\).
Suppose \($500\) is invested in an account at an annual interest rate of \(r=5.5\%\), compounded continuously.
- Let \(t\) denote the number of years after the initial investment and \(A(t)\) denote the amount of money in the account at time \(t\). Find a formula for \(A(t)\).
- Find the amount of money in the account after \(10\) years and after \(20\) years.
Solution
a. If \(P\) dollars are invested in an account at an annual interest rate \(r\), compounded continuously, then \(A(t)=Pe^{rt}\). Here \(P=$500\) and \(r=0.055\). Therefore, \(A(t)=500e^{0.055t}\).
b. After \(10\) years, the amount of money in the account is
\(A(10)=500e^{0.055⋅10}=500e^{0.55}≈$866.63\).
After \(20\) years, the amount of money in the account is
\(A(20)=500e^{0.055⋅20}=500e^{1.1}≈$1,502.08\).
If \($750\) is invested in an account at an annual interest rate of \(4\%\), compounded continuously, find a formula for the amount of money in the account after \(t\) years. Find the amount of money after \(30\) years.
- Hint
-
\(A(t)=Pe^{rt}\)
- Answer
-
\(A(t)=750e^{0.04t}\). After \(30\) years, there will be approximately \($2,490.09\).
Logarithmic Functions
Using our understanding of exponential functions, we can discuss their inverses, which are the logarithmic functions. These come in handy when we need to consider any phenomenon that varies over a wide range of values, such as the pH scale in chemistry or decibels in sound levels.
The exponential function \(f(x)=b^x\) is one-to-one, with domain \((−∞,∞)\) and range \((0,∞)\). Therefore, it has an inverse function, called the logarithmic function with base \(b\). For any \(b>0,\, b≠1\), the logarithmic function with base \(b\), denoted \(\log_b\), has domain \((0,∞)\) and range \((−∞,∞)\),and satisfies
\[\log_b(x)=y \nonumber \]
if and only if \(b^y=x\).
For example,
\[\log_2(8)=3\nonumber \]
since \(2^3=8\),
\[\log_{10}\left(\dfrac{1}{100}\right)=−2 \nonumber \]
since \(10^{−2}=\dfrac{1}{10^2}=\dfrac{1}{100}\),
\[\log_b(1)=0 \nonumber \]
since \(b^0=1\) for any base \(b>0\).
Furthermore, since \(y=\log_b(x)\) and \(y=b^x\) are inverse functions,
\[\log_b(b^x)=x \nonumber \]
and
\[b^{\log_b(x)}=x. \nonumber \]
The most commonly used logarithmic function is the function \(\log_e\). Since this function uses natural \(e\) as its base, it is called the natural logarithm. Here we use the notation \(\ln (x)\) or \(\ln x\) to mean \(\log_e(x)\). For example,
\[ \begin{align*} \ln (e) &=\log_e(e)=1 \\[4pt] \ln (e^3) &=\log_e(e^3)=3 \\[4pt] \ln (1) &=\log_e(1)=0. \end{align*}\]
Since the functions \(f(x)=e^x\) and \(g(x)=\ln (x)\) are inverses of each other,
\(\ln (e^x)=x\) and \(e^{\ln x}=x\),
and their graphs are symmetric about the line \(y=x\) (Figure \(\PageIndex{4}\)).
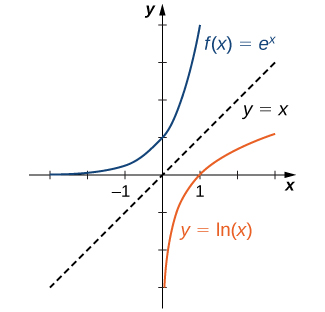 Figure \(\PageIndex{4}\): The functions \(y=e^x\) and \(y=\ln (x)\) are inverses of each other, so their graphs are symmetric about the line \(y=x\).
Figure \(\PageIndex{4}\): The functions \(y=e^x\) and \(y=\ln (x)\) are inverses of each other, so their graphs are symmetric about the line \(y=x\).
In general, for any base \(b>0\), \(b≠1\), the function \(g(x)=\log_b(x)\) is symmetric about the line \(y=x\) with the function \(f(x)=b^x\). Using this fact and the graphs of the exponential functions, we graph functions \(\log_b\) for several values of \(b>1\) ( Figure \(\PageIndex{5}\)).
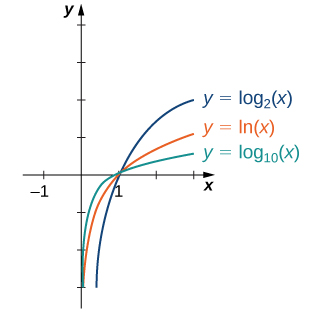 Figure \(\PageIndex{5}\): Graphs of \(y=\log_b(x)\) are depicted for \(b=2,\,e,\,10\).
Figure \(\PageIndex{5}\): Graphs of \(y=\log_b(x)\) are depicted for \(b=2,\,e,\,10\).
Before solving some equations involving exponential and logarithmic functions, let’s review the basic properties of logarithms.
If \(a,\,b,\,c>0,\,b≠1\), and \(r\) is any real number, then
- Product property
\[\log_b(ac)=\log_b(a)+\log_b(c) \label{productprop} \]
- Quotient property
\[\log_b \left(\dfrac{a}{c} \right)=\log_b(a)−\log_b(c) \label{quotientprop} \]
- Power property
\[\log_b(a^r)=r\log_b(a) \label{powerprop} \]
Solve each of the following equations for \(x\).
- \(5^x=2\)
- \(e^x+6e^{−x}=5\)
Solution
a. Applying the natural logarithm function to both sides of the equation, we have
\(\ln 5^x=\ln 2\).
Using the power property of logarithms,
\(x\ln 5=\ln 2.\)
Therefore,
\[x= \dfrac{\ln 2}{\ln 5}. \nonumber \]
b. Multiplying both sides of the equation by \(e^x\),we arrive at the equation
\(e^{2x}+6=5e^x\).
Rewriting this equation as
\(e^{2x}−5e^x+6=0\),
we can then rewrite it as a quadratic equation in \(e^x\):
\((e^x)^2−5(e^x)+6=0.\)
Now we can solve the quadratic equation. Factoring this equation, we obtain
\((e^x−3)(e^x−2)=0.\)
Therefore, the solutions satisfy \(e^x=3\) and \(e^x=2\). Taking the natural logarithm of both sides gives us the solutions \(x=\ln 3,\ln 2\).
Solve
\[e^{2x}/(3+e^{2x})=1/2. \nonumber \]
- Hint
-
First solve the equation for \(e^{2x}\)
- Answer
-
\(x=\dfrac{\ln 3}{2}\).
Solve each of the following equations for \(x\).
- \(\ln \left(\dfrac{1}{x}\right)=4\)
- \(\log_{10}\sqrt{x}+\log_{10}x=2\)
- \(\ln (2x)−3\ln (x^2)=0\)
Solution
a. By the definition of the natural logarithm function,
\(\ln \left(\dfrac{1}{x} \right)=4\)
- if and only if \(e^4=\dfrac{1}{x}\).
Therefore, the solution is \(x=1/e^4\).
b. Using the product (Equation \ref{productprop}) and power (Equation \ref{powerprop}) properties of logarithmic functions, rewrite the left-hand side of the equation as
\[\begin{align*} \log_{10}\sqrt{x} + \log_{10}x &= \log_{10} x \sqrt{x} \\[4pt] &= \log_{10}x^{3/2} \\[4pt] &= \dfrac{3}{2}\log_{10}x. \end{align*}\]
Therefore, the equation can be rewritten as
\(\dfrac{3}{2}\log_{10}x=2\)
or
\(\log_{10}x=\dfrac{4}{3}\).
The solution is \(x=10^{4/3}=10\sqrt[3]{10}\).
c. Using the power property (Equation \ref{powerprop}) of logarithmic functions, we can rewrite the equation as \(\ln (2x)−\ln (x^6)=0\).
Using the quotient property (Equation \ref{quotientprop}), this becomes
\(\ln \left(\dfrac{2}{x^5}\right)=0\)
Therefore, \(2/x^5=1\), which implies \(x=\sqrt[5]{2}\). We should then check for any extraneous solutions.
Solve \(\ln (x^3)−4\ln (x)=1\).
- Hint
-
First use the power property, then use the product property of logarithms.
- Answer
-
\(x=\dfrac{1}{e}\)
When evaluating a logarithmic function with a calculator, you may have noticed that the only options are \(\log_{10}\) or \(\log\), called the common logarithm, or \(\ln\), which is the natural logarithm. However, exponential functions and logarithm functions can be expressed in terms of any desired base \(b\). If you need to use a calculator to evaluate an expression with a different base, you can apply the change-of-base formulas first. Using this change of base, we typically write a given exponential or logarithmic function in terms of the natural exponential and natural logarithmic functions.
Let \(a>0,\,b>0\), and \(a≠1,\,b≠1\).
1. \(a^x=b^{x \log_ba}\) for any real number \(x\).
If \(b=e\), this equation reduces to \(a^x=e^{x \log_ea}=e^{x \ln a}\).
2. \(\log_ax=\dfrac{\log_bx}{\log_ba}\) for any real number \(x>0\).
If \(b=e\), this equation reduces to \(\log_ax=\dfrac{\ln x}{\ln a}\).
For the first change-of-base formula, we begin by making use of the power property of logarithmic functions. We know that for any base \(b>0,\, b≠1\), \(\log_b(a^x)=x \log_ba\). Therefore,
\(b^{\log_b(a^x)}\)=\(b^{x \log_ba}\).
In addition, we know that \(b^x\) and \(\log_b(x)\) are inverse functions. Therefore,
\(b^{\log_b(a^x)}=a^x\).
Combining these last two equalities, we conclude that \(a^x=b^{x \log_ba}\).
To prove the second property, we show that
\((\log_ba)⋅(\log_ax)=\log_bx.\)
Let \(u=\log_ba,v=\log_ax\), and \(w=\log_bx\). We will show that \(u⋅v=w\). By the definition of logarithmic functions, we know that \(b^u=a,\, a^v=x\), and \(b^w=x\). From the previous equations, we see that
\(b^{uv}=(b^u)^v=a^v=x=b^w.\)
Therefore, \(b^{uv}=b^w\). Since exponential functions are one-to-one, we can conclude that \(u⋅v=w\).
\(\square\)
Use a calculating utility to evaluate \(\log_37\) with the change-of-base formula presented earlier.
Solution
Use the second equation with \(a=3\) and \(b=e\): \(\log_37=\dfrac{\ln 7}{\ln 3}≈1.77124\).
Use the change-of-base formula and a calculating utility to evaluate \(\log_46\).
- Hint
-
Use the change of base to rewrite this expression in terms of expressions involving the natural logarithm function.
- Answer
-
\(\log_46 = \dfrac{\ln 6}{\ln 4} \approx 1.29248\)
In 1935, Charles Richter developed a scale (now known as the Richter scale) to measure the magnitude of an earthquake. The scale is a base-10 logarithmic scale, and it can be described as follows: Consider one earthquake with magnitude \(R_1\) on the Richter scale and a second earthquake with magnitude \(R_2\) on the Richter scale. Suppose \(R_1>R_2\), which means the earthquake of magnitude \(R_1\) is stronger, but how much stronger is it than the other earthquake?
 Figure \(\PageIndex{6}\): (credit: modification of work by Robb Hannawacker, NPS)
Figure \(\PageIndex{6}\): (credit: modification of work by Robb Hannawacker, NPS)
A way of measuring the intensity of an earthquake is by using a seismograph to measure the amplitude of the earthquake waves. If \(A_1\) is the amplitude measured for the first earthquake and \(A_2\) is the amplitude measured for the second earthquake, then the amplitudes and magnitudes of the two earthquakes satisfy the following equation:
\(R_1−R_2=\log_{10}\left(\dfrac{A1}{A2}\right)\).
Consider an earthquake that measures 8 on the Richter scale and an earthquake that measures 7 on the Richter scale. Then,
\(8−7=\log_{10}\left(\dfrac{A1}{A2}\right)\).
Therefore,
\(\log_{10}\left(\dfrac{A1}{A2}\right)=1\),
which implies \(A_1/A_2=10\) or \(A_1=10A_2\). Since \(A_1\) is 10 times the size of \(A_2\), we say that the first earthquake is 10 times as intense as the second earthquake. On the other hand, if one earthquake measures 8 on the Richter scale and another measures 6, then the relative intensity of the two earthquakes satisfies the equation
\(\log_{10}\left(\dfrac{A1}{A2}\right)=8−6=2\).
Therefore, \(A_1=100A_2\).That is, the first earthquake is 100 times more intense than the second earthquake.
How can we use logarithmic functions to compare the relative severity of the magnitude 9 earthquake in Japan in 2011 with the magnitude 7.3 earthquake in Haiti in 2010?
Solution
To compare the Japan and Haiti earthquakes, we can use an equation presented earlier:
\(9−7.3=\log_{10}\left(\dfrac{A1}{A2}\right)\).
Therefore, \(A_1/A_2=10^{1.7}\), and we conclude that the earthquake in Japan was approximately 50 times more intense than the earthquake in Haiti.
Compare the relative severity of a magnitude \(8.4\) earthquake with a magnitude \(7.4\) earthquake.
- Hint
-
\(R_1−R_2=\log_{10}(A1/A2)\).
- Answer
-
The magnitude \(8.4\) earthquake is roughly \(10\) times as severe as the magnitude \(7.4\) earthquake.
Hyperbolic Functions
The hyperbolic functions are defined in terms of certain combinations of \(e^x\) and \(e^{−x}\). These functions arise naturally in various engineering and physics applications, including the study of water waves and vibrations of elastic membranes. Another common use for a hyperbolic function is the representation of a hanging chain or cable, also known as a catenary (Figure \(\PageIndex{7}\)). If we introduce a coordinate system so that the low point of the chain lies along the \(y\)-axis, we can describe the height of the chain in terms of a hyperbolic function. First, we define the hyperbolic functions.
 Figure \(\PageIndex{7}\):The shape of a strand of silk in a spider’s web can be described in terms of a hyperbolic function. The same shape applies to a chain or cable hanging from two supports with only its own weight. (credit: “Mtpaley”, Wikimedia Commons)
Figure \(\PageIndex{7}\):The shape of a strand of silk in a spider’s web can be described in terms of a hyperbolic function. The same shape applies to a chain or cable hanging from two supports with only its own weight. (credit: “Mtpaley”, Wikimedia Commons)
Hyperbolic cosine
\(\cosh x=\dfrac{e^x+e^{−x}}{2}\)
Hyperbolic sine
\(\sinh x=\dfrac{e^x−e^{−x}}{2}\)
Hyperbolic tangent
\(\tanh x=\dfrac{\sinh x}{\cosh x}=\dfrac{e^x−e^{−x}}{e^x+e^{−x}}\)
Hyperbolic cosecant
\(\operatorname{csch}x=\dfrac{1}{\sinh x}=\dfrac{2}{e^x−e^{−x}}\)
Hyperbolic secant
\(\operatorname{sech}x=\dfrac{1}{\cosh x}=\dfrac{2}{e^x+e^{−x}}\)
Hyperbolic cotangent
\(\coth x=\dfrac{\cosh x}{\sinh x}=\dfrac{e^x+e^{−x}}{e^x−e^{−x}}\)
The name \(\cosh\) rhymes with “gosh,” whereas the name \(\sinh\) is pronounced “cinch.” \(\operatorname{Tanh}, \,\operatorname{sech}, \, \operatorname{csch},\) and \(\coth\) are pronounced “tanch,” “seech,” “coseech,” and “cotanch,” respectively.
Using the definition of \(\cosh(x)\) and principles of physics, it can be shown that the height of a hanging chain, such as the one in Figure \(\PageIndex{8}\), can be described by the function \(h(x)=a\cosh(x/a) + c\) for certain constants \(a\) and \(c\).
But why are these functions called hyperbolic functions? To answer this question, consider the quantity \(\cosh^2 t − \sinh^2 t\). Using the definition of \(\cosh\) and \(\sinh\), we see that
\[\cosh^2 t − \sinh^2 t=\dfrac{e^{2t}+2+e^{−2t}}{4}−\dfrac{e^{2t}−2+e^{−2t}}{4}=1. \nonumber \]
This identity is the analog of the trigonometric identity \(\cos^2 t + \sin^2 t=1\). Here, given a value \(t\), the point \((x,y)=(\cosh t,\,\sinh t)\) lies on the unit hyperbola \(x^2−y^2=1\) (Figure \(\PageIndex{8}\)).
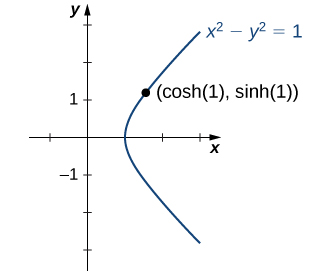 Figure \(\PageIndex{8}\): The unit hyperbola \(\cosh^2 t − \sinh^2 t=1\).
Figure \(\PageIndex{8}\): The unit hyperbola \(\cosh^2 t − \sinh^2 t=1\).
Graphs of Hyperbolic Functions
To graph \(\cosh x\) and \(\sinh x\), we make use of the fact that both functions approach \((1/2)e^x\) as \(x→∞\), since \(e^{−x}→0\) as \(x→∞\). As \(x→−∞,\cosh x\) approaches \(1/2e^{−x}\), whereas \(\sinh x\) approaches \(−1/2e^{−x}\). Therefore, using the graphs of \(1/2e^x,1/2e^{−x}\), and \(−1/2e^{−x}\) as guides, we graph \(\cosh x\) and \(\sinh x\). To graph \(\tanh x\), we use the fact that \(\tanh(0)=0\), \(−1<\tanh(x)<1\) for all \(x\), \(\tanh x→1\) as \(x→∞\), and \(\tanh x→−1\) as \(x→−∞\). The graphs of the other three hyperbolic functions can be sketched using the graphs of \(\cosh x\), \(\sinh x\), and \(\tanh x\) (Figure \(\PageIndex{9}\)).
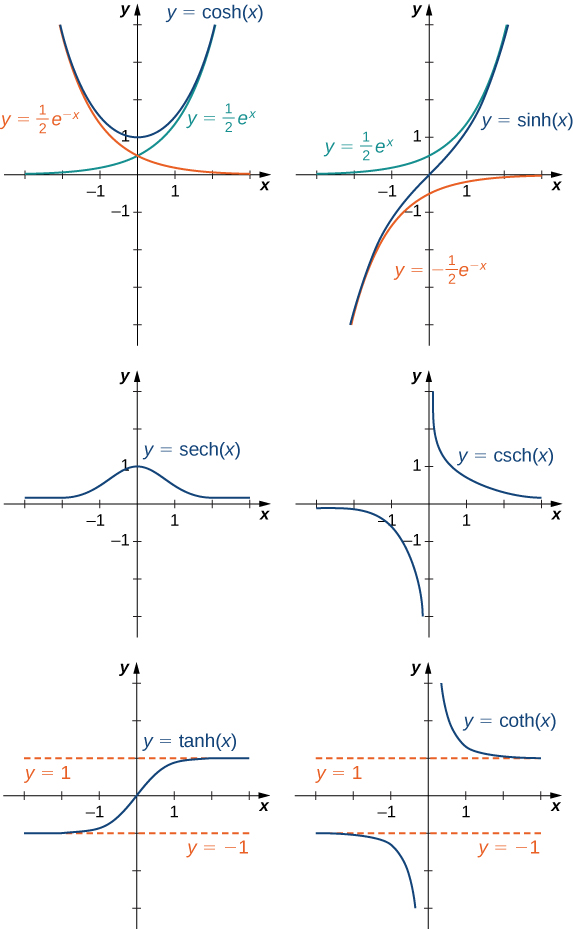 Figure \(\PageIndex{9}\): The hyperbolic functions involve combinations of \(e^x\) and \(e^{−x}\).
Figure \(\PageIndex{9}\): The hyperbolic functions involve combinations of \(e^x\) and \(e^{−x}\).
Identities Involving Hyperbolic Functions
The identity \(\cosh^2 t−\sinh^2 t = 1\), shown in Figure \(\PageIndex{8}\), is one of several identities involving the hyperbolic functions, some of which are listed next. The first four properties follow easily from the definitions of hyperbolic sine and hyperbolic cosine. Except for some differences in signs, most of these properties are analogous to identities for trigonometric functions.
- \(\cosh(−x)=\cosh x\)
- \(\sinh(−x)=−\sinh x\)
- \(\cosh x+\sinh x=e^x\)
- \(\cosh x−\sinh x=e^{−x}\)
- \(\cosh^2 x−\sinh^2 x=1\)
- \(1−\tanh^2 x=\operatorname{sech}^2 x\)
- \(\coth^2 x −1=\operatorname{csch}^2 x\)
- \(\sinh(x±y)=\sinh x \cosh y ± \cosh x \sinh y\)
- \(\cosh(x±y)=\cosh x \cosh y ± \sinh x \sinh y\)
- Simplify \(\sinh(5\ln x)\).
- If \(\sinh x=3/4\), find the values of the remaining five hyperbolic functions.
Solution:
a. Using the definition of the \(\sinh\) function, we write
\(\sinh(5\ln x)=\dfrac{e^{5\ln x}−e^{−5\ln x}}{2}=\dfrac{e^{\ln (x^5)}−e^{\ln (x^{−5})}}{2}=\dfrac{x^5−x^{−5}}{2}.\)
b. Using the identity \(\cosh^2 x − \sinh^2 x=1\),we see that
\(\cosh^2 x=1+\left(\frac{3}{4}\right)^2=\dfrac{25}{16}.\)
Since \(\cosh x≥1\) for all \(x\), we must have \(\cosh x=5/4\). Then, using the definitions for the other hyperbolic functions, we conclude that \(\tanh x=3/5,\operatorname{csch}x=4/3,\operatorname{sech}x=4/5\), and \(\coth x=5/3\).
Simplify \(\cosh(2\ln x)\).
- Hint
-
Use the definition of the \(\cosh\) function and the power property of logarithm functions.
- Answer
-
\((x^2+x^{−2})/2\)
Inverse Hyperbolic Functions
From the graphs of the hyperbolic functions, we see that all of them are one-to-one except \(\cosh x\) and \(\operatorname{sech}x\). If we restrict the domains of these two functions to the interval \([0,∞),\) then all the hyperbolic functions are one-to-one, and we can define the inverse hyperbolic functions. Since the hyperbolic functions themselves involve exponential functions, the inverse hyperbolic functions involve logarithmic functions.
\[\begin{align*} &\sinh^{−1}x =\operatorname{arcsinh}x=\ln \left(x+\sqrt{x^2+1}\right) & & \cosh^{−1}x =\operatorname{arccosh}x=\ln \left(x+\sqrt{x^2−1}\right)\\[4pt]
&\tanh^{−1}x=\operatorname{arctanh}x=\dfrac{1}{2}\ln \left(\dfrac{1+x}{1−x}\right) & & \coth^{−1}x =\operatorname{arccot}x=\frac{1}{2}\ln \left(\dfrac{x+1}{x−1}\right)\\[4pt]
&\operatorname{sech}^{−1}x=\operatorname{arcsech}x=\ln \left(\dfrac{1+\sqrt{1−x^2}}{x}\right) & & \operatorname{csch}^{−1}x=\operatorname{arccsch}x=\ln \left(\dfrac{1}{x}+\dfrac{\sqrt{1+x^2}}{|x|}\right) \end{align*}\]
Let’s look at how to derive the first equation. The others follow similarly. Suppose \(y=\sinh^{−1}x\). Then, \(x=\sinh y\) and, by the definition of the hyperbolic sine function, \(x=\dfrac{e^y−e^{−y}}{2}\). Therefore,
\(e^y−2x−e^{−y}=0.\)
Multiplying this equation by \(e^y\), we obtain
\(e^{2y}−2xe^y−1=0\).
This can be solved like a quadratic equation, with the solution
\(e^y=\dfrac{2x±\sqrt{4x^2+4}}{2}=x±\sqrt{x^2+1}\).
Since \(e^y>0\),the only solution is the one with the positive sign. Applying the natural logarithm to both sides of the equation, we conclude that
\(y=\ln (x+\sqrt{x^2+1}).\)
Evaluate each of the following expressions.
\(\sinh^{−1}(2)\)
\(\tanh^{−1}(1/4)\)
Solution:
\[\sinh^{−1}(2)=\ln (2+\sqrt{2^2+1})=\ln (2+\sqrt{5})≈1.4436\nonumber \]
\[\tanh^{−1}(1/4)=\frac{1}{2}\ln \left(\dfrac{1+1/4}{1−1/4}\right)=\frac{1}{2}\ln \left(\dfrac{5/4}{3/4}\right)=\frac{1}{2}\ln \left(\dfrac{5}{3}\right)≈0.2554\nonumber \]
Evaluate \(\tanh^{−1}(1/2)\).
- Hint
-
Use the definition of \(\tanh^{−1}x\) and simplify.
- Answer
-
\(\dfrac{1}{2}\ln (3)≈0.5493\).
Key Concepts
- The exponential function \(y=b^x\) is increasing if \(b>1\) and decreasing if \(0<b<1\). Its domain is \((−∞,∞)\) and its range is \((0,∞)\).
- The logarithmic function \(y=\log_b(x)\) is the inverse of \(y=b^x\). Its domain is \((0,∞)\) and its range is \((−∞,∞).\)
- The natural exponential function is \(y=e^x\) and the natural logarithmic function is \(y=\ln x=\log_ex.\)
- Given an exponential function or logarithmic function in base \(a\), we can make a change of base to convert this function to any base \(b>0\), \(b≠1.\) We typically convert to base \(e\).
- The hyperbolic functions involve combinations of the exponential functions \(e^x\) and \(e^{−x}.\) As a result, the inverse hyperbolic functions involve the natural logarithm.
Glossary
- base
- the number \(b\) in the exponential function \(f(x)=b^x\) and the logarithmic function \(f(x)=\log_bx\)
- exponent
- the value \(x\) in the expression \(b^x\)
- hyperbolic functions
- the functions denoted \(\sinh,\,\cosh,\,\operatorname{tanh},\,\operatorname{csch},\,\operatorname{sech},\) and \(\coth\), which involve certain combinations of \(e^x\) and \(e^{−x}\)
- inverse hyperbolic functions
- the inverses of the hyperbolic functions where \(\cosh\) and \( \operatorname{sech}\) are restricted to the domain \([0,∞)\);each of these functions can be expressed in terms of a composition of the natural logarithm function and an algebraic function
- natural exponential function
- the function \(f(x)=e^x\)
- natural logarithm
- the function \(\ln x=\log_ex\)
- number e
- as \(m\) gets larger, the quantity \((1+(1/m)^m\) gets closer to some real number; we define that real number to be \(e;\) the value of \(e\) is approximately \(2.718282\)

