Skip to main content
Statistics LibreTexts

10.1: Chi-Square Distribution

  1. Last updated
  2. Save as PDF
  • Page ID
    24065

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

    \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

    \( \newcommand{\dsum}{\displaystyle\sum\limits} \)

    \( \newcommand{\dint}{\displaystyle\int\limits} \)

    \( \newcommand{\dlim}{\displaystyle\lim\limits} \)

    \( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

    ( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

    \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

    \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

    \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

    \( \newcommand{\Span}{\mathrm{span}}\)

    \( \newcommand{\id}{\mathrm{id}}\)

    \( \newcommand{\Span}{\mathrm{span}}\)

    \( \newcommand{\kernel}{\mathrm{null}\,}\)

    \( \newcommand{\range}{\mathrm{range}\,}\)

    \( \newcommand{\RealPart}{\mathrm{Re}}\)

    \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

    \( \newcommand{\Argument}{\mathrm{Arg}}\)

    \( \newcommand{\norm}[1]{\| #1 \|}\)

    \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

    \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    \( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

    \( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

    \( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

    \( \newcommand{\vectorC}[1]{\textbf{#1}} \)

    \( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

    \( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

    \( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

    \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

    \(\newcommand{\longvect}{\overrightarrow}\)

    \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

    \(\newcommand{\ket}[1]{\left| #1 \right>}\)
    \(\newcommand{\bra}[1]{\left< #1 \right|}\)
    \(\newcommand{\braket}[2]{\left< #1 \vphantom{#2} \right| \left. #2 \vphantom{#1} \right>}\)
    \(\newcommand{\braopket}[3]{\left< #1 \vphantom{#2}\vphantom{#3} \right| #2 \vphantom{#1}\vphantom{#3} \left| #3 \vphantom{#1}\vphantom{#2} \right>}\)
    \(\newcommand{\qmvec}[1]{\mathbf{\vec{#1}}}\)
    \(\newcommand{\op}[1]{\hat{\mathbf{#1}}}\)
    \(\newcommand{\expect}[1]{\langle #1 \rangle}\)
    \(\newcommand{\dfn}[1]{\emph{\textbf{#1}}}\)

    \(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)

    A \(\chi^{2}\) -distribution (chi-square, pronounced “ki-square”) is another special type of distribution for a continuous random variable. The sampling distribution for a variance and standard deviation follows a chi-square distribution.

    Properties of the \(\chi^{2}\) -distribution density curve:

    1. Right skewed starting at zero.
    2. The center and spread of a \(\chi^{2}\) -distribution are determined by the degrees of freedom with a mean = df and standard deviation = \(\sqrt{2df}\).
    3. Chi-square variables cannot be negative.
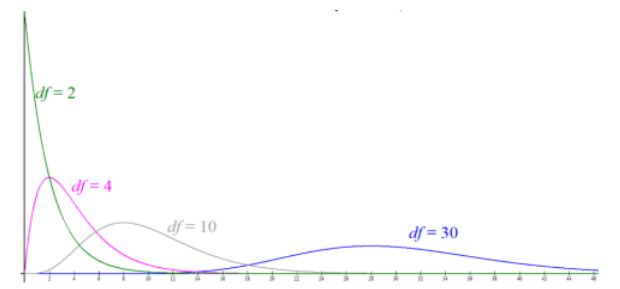
    4. As the degrees of freedom increase, the \(\chi^{2}\) -distribution becomes normally distributed for df > 50. Figure 10-1 shows \(\chi^{2}\) -distributions for df of 2, 4, 10, and 30.
    5. The total area under the curve is equal to 1, or 100%.
    clipboard_e4bc6fcabad9b911d3a268aeaf5de1162.png
    Figure 10-1

    We will use the \(\chi^{2}\) -distribution for hypothesis testing later in this chapter. For now, we are just learning how to find a critical value \(\chi_{\alpha}^{2}\).

    The symbol \(\chi_{\alpha}^{2}\) is the critical value on the \(\chi^{2}\) -distribution curve with area 1 – \(\alpha\) below the critical value and area \(\alpha\) above the critical value, as shown below in Figure 10-2.

    clipboard_edff4463e62adbaa4742b5fa29a80fb4d.png
    Figure 10-2

    Use technology to compute the critical value for the \(\chi^{2}\) -distribution.

    TI-84: Use the INVCHI2 program downloaded at Rachel Webb’s website: http://MostlyHarmlessStatistics.com. Start the program and enter the area \(\alpha\) and the df when prompted.

    TI-89: Go to the [Apps] Stat/List Editor, then select F5 [DISTR]. This will get you a menu of probability distributions. Arrow down to Inverse > Inverse Chi-Square and press [ENTER]. Enter the area 1 – \(\alpha\) to the left of the \(\chi\) value and the df into each cell. Press [ENTER].

    Excel: =CHISQ.INV(1 – \(\alpha\), df) or =CHISQ.INV.RT(\(\alpha\), df)

    Alternatively, use the following online calculator: https://homepage.divms.uiowa.edu/~mbognar/applets/chisq.html.

    Compute the critical value \(\chi_{\alpha}^{2}\) for a \(\alpha\) = 0.05 and df = 6.

    Solution

    Start by drawing the curve and determining the area in the right-tail as shown in Figure 10-3. Then use technology to find the critical value.

    clipboard_e7be50b99403a71daef1d9a363b5f5d48.png
    Figure 10-3

    In Excel there are two options. Use =CHISQ.INV(area in left-tail,df) or right-tail =CHISQ.INV.RT(area in righttail,df). For this example, then we would have \(\chi_{\alpha}^{2}\) =CHISQ.INV(0.95,6) or =CHISQ.INV.RT(0.05,6) = 12.5916.

    TI-89 use Distr > Inverse Chi-square with area 0.95 and df = 6

    clipboard_ea1a1baed623f4f3224c7d4d4dfa2fe6f.png

    This page titled 10.1: Chi-Square Distribution was last modified on Sun, 12 Mar 2023 17:55:06 GMT and is shared under a CC BY-SA 4.0 license and was authored, remixed, and/or curated by Rachel Webb via source content that was edited to the style and standards of the LibreTexts platform.