9.3: Two Proportion Z-Test and Confidence Interval

This section will look at how to analyze a difference in the proportions for two independent samples. As with all other hypothesis tests and confidence intervals, the process of testing is the same, though the formulas and assumptions are different.

There are three types of hypothesis tests for comparing the difference in 2 population proportions p₁ – p₂, see Figure 9-7.

Figure 9-7

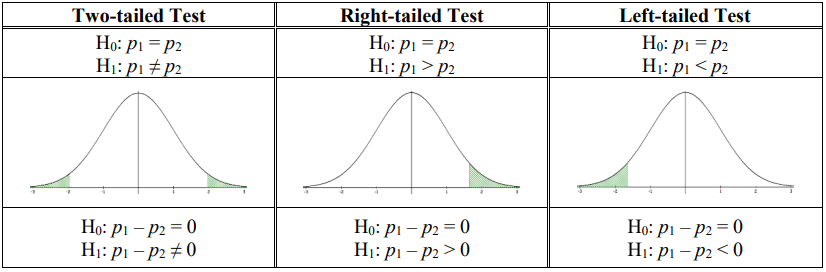
Note that for our purposes, p₁ – p₂ = 0. We could also use a variant of this model to test for a magnitude difference for when p₁ – p₂ ≠ 0, but we will not cover that scenario.

The z-test is a statistical test for comparing the proportions from two populations. It can be used when the samples are independent, \(n_{1} \hat{p}_{1}\) ≥ 10, \(n_{1} \hat{q}_{1}\) ≥ 10, \(n_{2} \hat{p}_{2}\) ≥ 10, and \(n_{2} \hat{q}_{2}\) ≥ 10.

The formula for the z-test statistic is:

\(z=\frac{\left(\hat{p}_{1}-\hat{p}_{2}\right)-\left(p_{1}-p_{2}\right)}{\sqrt{\left(\hat{p} \cdot \hat{q}\left(\frac{1}{n_{1}}+\frac{1}{n_{2}}\right)\right)}}\)

Where \(\hat{p}=\frac{\left(x_{1}+x_{2}\right)}{\left(n_{1}+n_{2}\right)}=\frac{\left(\hat{p}_{1} \cdot n_{1}+\hat{p}_{2} \cdot n_{2}\right)}{\left(n_{1}+n_{2}\right)}, \quad \hat{q}=1-\hat{p}, \quad \hat{p}_{1}=\frac{x_{1}}{n_{1}}, \hat{p}_{2}=\frac{x_{2}}{n_{2}}\).

The pooled proportion \(\hat{p}\) is a weighted mean of the proportions and \(\hat{q}\) is the complement of \(\hat{p}\). Some texts or software may use different notation for the pooled proportion, note that \(\hat{p}=\bar{p}\).

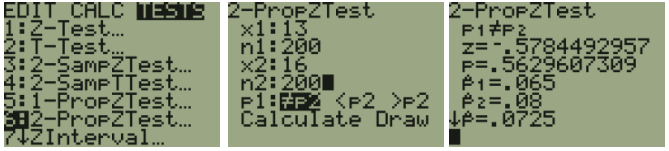
A vice principal wants to see if there is a difference between the number of students who are late to class for the first class of the day compared to the student’s class right after lunch. To test their claim to see if there is a difference in the proportion of late students between first and after lunch classes, the vice-principal randomly selects 200 students from first class and records if they are late, then randomly selects 200 students in their class after lunch and records if they are late. At the 0.05 level of significance, can a difference be concluded?

  First Class After Lunch Class Sample Size 200 200 Number of late students 13 16

Solution

Assumptions: We are comparing the proportion of late students’ first and after lunch classes. The number of “successes” and “failures” from each population must be greater than 10 ( = 13 ≥ 10, = 187 ≥ 10, = 16 ≥ 10, and = 184 ≥ 10). We must assume that the samples were independent.

Using the Traditional Method The claim is that there is a difference between the proportion of late students. Let population 1 be the first class, and population 2 be the class after lunch. Our claim would then be p₁ ≠ p₂.

The correct hypotheses are: H0: p₁ = p₂

H1: p₁ ≠ p₂.

Compute the \(z_{\alpha / 2}\) critical values. Draw and label the sampling distribution.

Use the inverse normal function invNorm(0.025,0,1) to get \(z_{\alpha / 2}\) = ±1.96. See Figure 9-8.

Figure 9-8

In order to compute the test statistic, we must first compute the following proportions:

\(\begin{array}{ll}
\hat{p}=\frac{\left(x_{1}+x_{2}\right)}{\left(n_{1}+n_{2}\right)}=\frac{(13+16)}{(200+200)}=0.0725 & \hat{q}=1-\hat{p}=1-0.0725=0.9275 \\
\hat{p}_{1}=\frac{x_{1}}{n_{1}}=\frac{13}{200}=0.065 & \hat{p}_{2}=\frac{x_{2}}{n_{2}}=\frac{16}{200}=0.08
\end{array}\)

The test statistic is, \(z=\frac{\left(\hat{p}_{1}-\hat{p}_{2}\right)-\left(p_{1}-p_{2}\right)}{\sqrt{\left(\hat{p} \cdot \hat{q}\left(\frac{1}{n_{1}}+\frac{1}{n_{2}}\right)\right)}}=\frac{(0.065-0.08)}{\sqrt{\left(0.0725 \cdot 0.9275\left(\frac{1}{200}+\frac{1}{200}\right)\right)}}=-0.5784\).

Decision: Because the test statistic is between the critical values, we do not reject H₀.

Summary: There is not enough evidence to support any difference in the proportion of students that are late for their first class compared to the class after lunch.

TI-84: Press the [STAT] key, arrow over to the [TESTS] menu, arrow down to the option [6:2-PropZTest] and press the [ENTER] key. Type in the x₁, n₁, x₂, and n₂ arrow over to the \(\neq\), <, > sign that is the same in the problem’s alternative hypothesis statement, then press the [ENTER] key, arrow down to [Calculate] and press the [ENTER] key. The calculator returns the z-test statistic and the p-value.

TI-89: Go to the [Apps] Stat/List Editor, then press [2^nd] then F6 [Tests], then select 6: 2-PropZTest. Type in the x₁, n₁, x₂, and n2 arrow over to the \(\neq\), <, > and select the sign that is the same in the problem’s alternative hypothesis statement. Press the [ENTER] key to calculate. The calculator returns the z-test statistic, sample proportions, pooled proportion, and the p-value.

Two Proportions Z-Interval

A 100(1 – \(\alpha\))% confidence interval for the difference between two population proportions p₁ – p₂:

\(\left(\hat{p}_{1}-\hat{p}_{2}\right)-z_{\alpha / 2} \sqrt{\left(\frac{\hat{p}_{1} \hat{q}_{1}}{n_{1}}+\frac{\hat{p}_{2} \hat{q}_{2}}{n_{2}}\right)}<p_{1}-p_{2}<\left(\hat{p}_{1}-\hat{p}_{2}\right)+z_{\alpha / 2} \sqrt{\left(\frac{\hat{p}_{1} \hat{q}_{1}}{n_{1}}+\frac{\hat{p}_{2} \hat{q}_{2}}{n_{2}}\right)}\)

Or more compactly as \(\left(\hat{p}_{1}-\hat{p}_{2}\right) \pm z_{\alpha / 2} \sqrt{\left(\frac{\hat{p}_{1} \hat{q}_{1}}{n_{1}}+\frac{\hat{p}_{2} \hat{q}_{2}}{n_{2}}\right)}\)

The requirements are identical to the 2-proportion hypothesis test. Note that the standard error does not rely on a hypothesized proportion so do not use a confidence interval to make decisions based on a hypothesis statement.

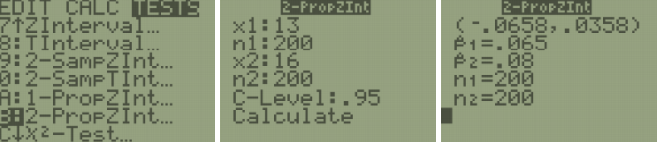
Find the 95% confidence interval for the difference in the proportion of late students in their first class and the proportion who are late to their class after lunch.

  First ClassAfter Lunch Class Sample Size 200 200 Number of late students 13 16

Solution

First, compute the following:

\(\hat{p}_{1}=\frac{x_{1}}{n_{1}}=\frac{13}{200}=0.065 \quad \hat{q}_{1}=1-\hat{p}_{1}=1-0.065=0.935\)

\(\hat{p}_{2}=\frac{x_{2}}{n_{2}}=\frac{16}{200} \quad=0.08 \quad \hat{q}_{2}=1-\hat{p}_{2}=1-0.08=0.92\)

Find the \(z_{\alpha / 2}\) critical value. Use the inverse normal to get \(z_{\alpha / 2}\) = 1.96.

Now substitute the numbers into the interval estimate: \(\left(\hat{p}_{1}-\hat{p}_{2}\right) \pm z_{\frac{\alpha}{2}} \sqrt{\left(\frac{\hat{p}_{1} \hat{q}_{1}}{n_{1}}+\frac{\hat{p}_{2} \hat{q}_{2}}{n_{2}}\right)}\)

\(\begin{aligned}
&\Rightarrow(0.065-0.08) \pm 1.96 \sqrt{\left(\frac{0.065 \cdot 0.935}{200}+\frac{0.08 \cdot 0.92}{200}\right)} \\
&\Rightarrow \quad-0.015 \pm 0.0508 \\
&\Rightarrow \quad(-0.0508,0.0358) .
\end{aligned}\)

Use interval notation (–0.0508, 0.0358) or standard notation –0.0508 < p₁ – p₂ < 0.0358. Note that we can have negative numbers here since we are taking the difference of two proportions.

Since p₁ – p₂ = 0 is in the interval, we are 95% confident that there is no difference in the proportion of late students between their first class or those who are late for their class after lunch.

TI-84: Press the [STAT] key, arrow over to the [TESTS] menu, arrow down to the option [2-PropZInterval] and press the [ENTER] key. Type in the x₁, n₁, x₂, n₂, the confidence level, then press the [ENTER] key, arrow down to [Calculate] and press the [ENTER] key. The calculator returns the confidence interval.

TI-89: Go to the [Apps] Stat/List Editor, then press [2^nd] then F7 [Ints], then select 6: 2-PropZInt. Type in the x₁, n₁, x₂, n₂, the confidence level, then press the [ENTER] key to calculate. The calculator returns the confidence interval.