6.4: Normal Distribution

Empirical Rule

Before looking at the process for finding the probabilities under a normal curve, recall the Empirical Rule that gives approximate values for areas under a bell-shaped distribution. The Empirical Rule, shown in Figure 6-10, is just an approximation for probability under any bell-shaped distribution and will only be used in this section to give you an idea of the size of the probability for different shaded areas. A more precise method for finding probabilities will be demonstrated using technology. Please do not use the empirical rule in the homework questions except for rough estimates.

The Empirical Rule (or 68-95-99.7 Rule)

In a bell-shaped distribution with mean μ and standard deviation σ,

• Approximately 68% of the observations fall within one standard deviation (σ) of the mean μ.
• Approximately 95% of the observations fall within two standard deviations (2σ) of the mean μ.
• Approximately 99.7% of the observations fall within three standard deviations (3σ) of the mean μ.

Gauss

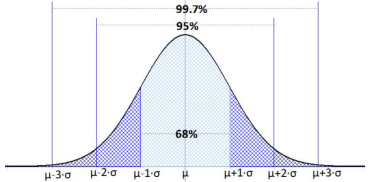
Figure 6-10

For now, we will be working with the most common bell-shaped probability distribution known as the normal distribution, also called the Gaussian distribution, named after the German mathematician Johann Carl Friedrich Gauss. See Figure 6-11.

Figure 6-11

A normal distribution is a special type of distribution for a continuous random variable. Normal distributions are important in statistics because many situations in the real world have normal distributions.

Properties of the normal density curve:

1. Symmetric bell-shaped.
2. Unimodal (one mode).
3. Centered at the mean μ= median = mode.
4. The total area under the curve is equal to 1 or 100%.
5. The spread of a normal distribution is determined by the standard deviation σ. The larger σ is, the more spread out the normal curve is from the mean.
6. Follows the Empirical Rule.

If a continuous random variable X has a Normal distribution with mean μ and standard deviation σ then the distribution is denoted as X~N(μ, σ). Any x values from a Normal distribution can be transformed or standardized into a standard Normal distribution by taking the z-score of x.

The formula for the normal probability density function is: \(f(x)=\frac{1}{\sigma \sqrt{2 \pi}} e^{\left(-\frac{1}{2}\left(\frac{x-\mu}{\sigma}\right)^{2}\right)}\). We will not be using this formula.

The probability is found by using integral calculus to find the area under the PDF curve. Prior to the handheld calculators and personal computers, there were probability tables made to look up these areas. This text does not use probability tables and will instead rely on technology to compute the area under the curve.

Every time the mean or standard deviation changes the shape of the normal distribution changes. The center of the normal curve will be the mean and the spread of the normal curve gets wider as the standard deviation gets larger.

Figure 6-12 compares two normal distributions N(0, 1) in green on the left and N(7, 6) in blue on the right.

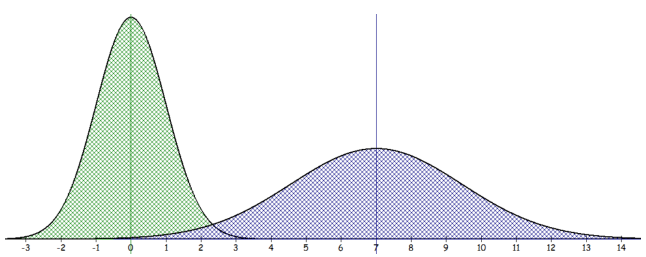
Figure 6-12

“‘So, what's odd about it?’

‘Nothing, it's Perfectly Normal.’”

(Adams, 2002)

6.4.1 Standard Normal Distribution

A normal distribution with mean μ = 0 and standard deviation σ = 1 is called the standard normal distribution.

The letter Z is used exclusively to denote a variable that has a standard normal distribution and is written Z ~ N(0, 1). A particular value of Z is denoted z (lower-case) and is referred to as a z-score.

Recall that a z-score is the number of standard deviations x is from the mean. Anytime you are asked to find a probability of Z use the standard normal distribution.

Standardizing and z-scores:

A z-score is the number of standard deviations an observation x is above or below the mean μ. If the z-score is negative, x is below the mean. If the z-score is positive, x is above the mean.

If x is an observation from a distribution that has mean μ and standard deviation σ, the standardized value of x (or z-score) is \(\mathrm{z}=\frac{x-\mu}{\sigma}\).

To find the area under the probability density curve involves calculus so we will need to rely on technology to find the area.

Compute the area under the standard normal distribution to the left of z = 1.39.

Solution

First, draw a bell-shaped distribution with 0 in the middle as shown in Figure 6-13. Mark 1.39 on the number line and shade to the left of z = 1.39.

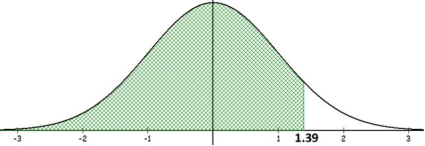
Figure 6-13

Note that the lower value of the shaded region is -∞, which the TI-84 does not have. Instead we use a really small number in scientific notation -1E99 or -1*1099 (make sure you use the negative sign (-) not the minus – sign.

The normalcdf on the calculator needs the lower and upper value of the shaded area followed by the mean and standard deviation. (The TI-89 uses -∞ for the lower boundary instead of -1E99.)

TI-84: Press [2nd] [DISTR] menu, select the normalcdf. Then type in the lower value, upper value, mean = 0, standard deviation = 1 to get normalcdf(-1E99,1.39,0,1) = 0.9177, which is your answer. The area under the curve is equivalent to the probability of getting a z-score less than 1.39, or P(Z < 1.39) = 0.9177.

TI-89: Go to the [Apps] Stat/List Editor, then select F5 [DISTR]. This will get you a menu of probability distributions. Arrow down to Normal Cdf and press [ENTER]. Enter the values for the lower z value (z1), upper z value (z2), μ = 0, and σ = 1 into each cell. Press [ENTER]. This is the cumulative distribution function and will return P(z1 < Z < z2). For a left-tail area use a lower bound of negative infinity (-∞), and for a right-tail area use an upper bound infinity (∞).

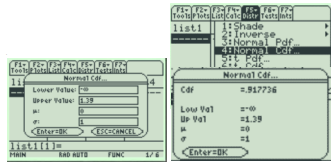
Excel: For Excel the program will only find the area to the left of a point. Therefore, if we want to find the area to the right of a point or between two points there will be one extra step. Use the formula =NORM.S.DIST(1.39,TRUE).

Compute the probability of getting a z-score between –1.37 and 1.68.

Solution

P(-1.37 ≤ Z ≤ 1.68) is the same as finding the area under the curve between –1.37 and 1.68. First, draw a bell-shaped distribution and identify the two points on the number line. Shade the area between the two points as shown in Figure 6-14.

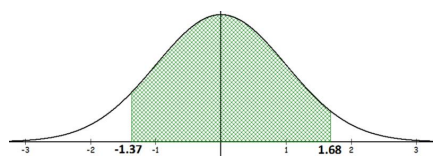
Figure 6-14

TI Calculator: P(-1.37 ≤ Z ≤ 1.68) = normalcdf(-1.37,1.68,0,1) = 0.8682.

Excel: P(-1.37 ≤ Z ≤ 1.68) =NORM.S.DIST(1.68,TRUE)-NORM.S.DIST(-1.37,TRUE) = 0.8682.

Using Excel or TI-Calculator to Find Standard Normal Distribution

As you read through a problem look for some of the following key phrases in Figure 6-15. Once you find the phrase then match up to what sign you would use and then use the table to walk you through using Excel or the calculator. Note that we could also use the NORM.DIST function with µ = 0 and σ = 1.

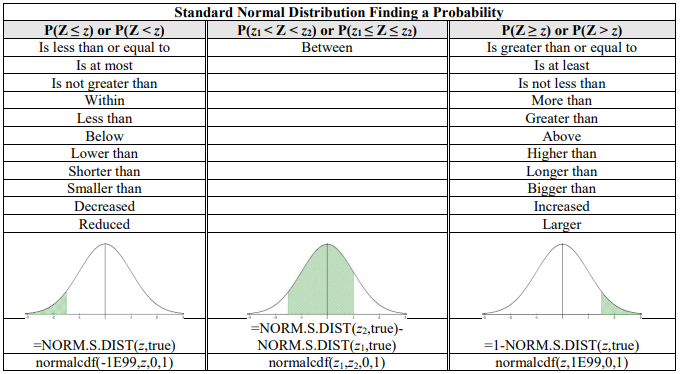
Figure 6-15

Compute the area under the standard normal distribution that is 2 standard deviations from the mean.

Solution

A rough estimate using the Empirical Rule would be 0.95, however since this is not just any bell-shaped distribution, we will find the P(-2 ≤ Z ≤ 2). Draw and shade the curve as in Figure 6-16.

TI Calculator: P(-2 ≤ Z ≤ 2) = normalcdf(-2,2,0,1) = 0.9545.

Excel: P(-2 ≤ Z ≤ 2) =NORM.S.DIST(2,TRUE) -NORM.S.DIST(-2,TRUE) = 0.9545.

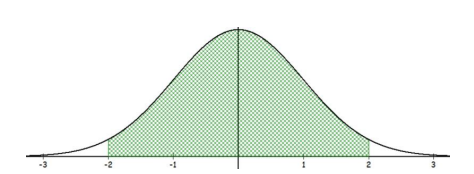
Figure 6-16

Compute the area to the right of z = 1.

Solution

Draw and shade the curve to find P(Z > 1). See Figure 6-17.

TI Calculator: P(Z > 1) = normalcdf(1,1E99,0,1) = 0.1587.

Excel: P(Z > 1) = 1-NORM.S.DIST(1,TRUE) = 0.1587.

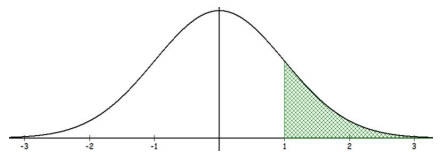
Figure 6-17

6.4.2 Applications of the Normal Distribution

Many variables are nearly normal, but none are exactly normal. Thus, the normal distribution, while not perfect for any single problem, is very useful for a variety of problems. Variables such as SAT scores and heights of United States adults closely follow the normal distribution. Note that the Excel function NORM.S.DIST is for a standard normal when µ = 0 and σ = 1

Using Excel or TI-Calculator to Find Normal Distribution Probabilities

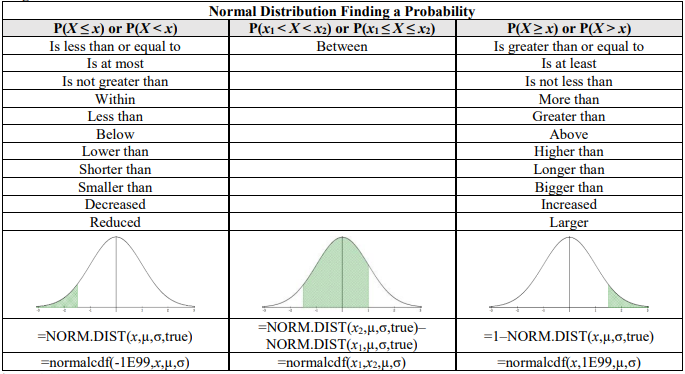
Figure 6-18

TI-84: Press [2nd] [DISTR]. This will show a menu of probability distributions. Arrow down to 2:normalcdf( and press [ENTER]. This puts normalcdf( on the home screen. Enter the values for the lower x value (x1), upper x value (x2), μ, and σ with a comma between each. Press [ENTER]. This is the cumulative distribution function and will return P(x1 < X < x2). For example, to find P(80 < X < 110) when the mean is 100 and the standard deviation is 20, you should have normalcdf(80,110,100,20). If you leave out the μ and σ, then the default is the standard normal distribution. For a left-tail area use a lower bound of –1E99 (negative infinity), (press [2nd] [EE] to get E) and for a right-tail area use an upper bound of 1E99 (infinity). For example, to find P(Z < -1.37) you should have normalcdf(-1E99,-1.37).

TI-89: Go to the [Apps] Stat/List Editor, select F5 [DISTR]. This will show a menu of probability distributions. Arrow down to Normal Cdf and press [ENTER]. Enter the values for the lower x value (x1), upper x value (x2), μ, and σ into each cell. Press [ENTER]. This is the cumulative distribution function and will return P(x1 < X < x2). For example, to find P(80 < X < 110) when the mean is 100 and the standard deviation is 20, you should have in the following order 80, 110, 100, 20. If you have a z-score, use μ = 0 and σ = 1, then you will get a standard normal distribution. For a left-tail area use a lower bound of negative infinity (-∞), and for a right-tail area use an upper bound infinity (∞).

“The Hitchhiker's Guide to the Galaxy offers this definition of the word "Infinite." Infinite: Bigger than the biggest thing ever and then some. Much bigger than that in fact, really amazingly immense, a totally stunning size, "wow, that's big," time. Infinity is just so big that by comparison, bigness itself looks really titchy. Gigantic multiplied by colossal multiplied by staggeringly huge is the sort of concept we're trying to get across here.”

(Adams, 2002)

Let X be the height of 15-year old boys in the United States. Studies show that the heights of 15-year old boys in the United States are normally distributed with average height 67 inches and a standard deviation of 2.5 inches. Compute the probability of randomly selecting one 15-year old boy who is 69.5 inches or taller.

Solution

Find P(X ≥ 69.5) where X ~ N(67, 2.5). Draw the curve and label the mean, then shade the area to the right of 69.5.

Figure 6-19

First, standardize the value of x = 69.5 using the z-score formula \(z=\frac{x-\mu}{\sigma}\), where μ = 67 and σ = 2.5. The standardized value of x = 69.5 is \(z=\frac{69.5-67}{2.5}\) = 1.

Now using the standard normal distribution and shading the area to the right of z = 1 gives:

TI calculator: P(Z ≥ 1) = normalcdf(1,1E99,0,1) = 0.158655.

Excel: P(Z ≥ 1) = 1-NORM.S.DIST(1,TRUE) = 0.158655.

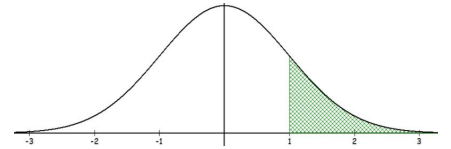
Figure 6-20

We could also use the Empirical rule to approximate P(X ≥ 69.5) because this is the same as being more than one standard deviation above the mean. Do you see why this makes sense?

If we were to add a standard deviation to 67 we would get 69.5. Thus P(X ≥ 69.5) \(\approx\) 0.16, which is close to our 15.87% using the standard normal distribution. The Empirical rule only gives an approximate value though.

The process of standardizing the X value was started so that we could use the standard normal distribution table to look up probabilities instead of using caclulus. With technology, you no longer have to standardize first, we can just find P(X ≥ 69.5).

TI calculator: P(X ≥ 69.5) = normalcdf(69.5, 1E99,67,2.5) \(\approx\) 0.158655 (The TI-89 use ∞ for the upper boundary instead of 1E99).

Excel: P(X ≥ 69.5) =1 – NORM.DIST(69.5,67,2.5,TRUE) = 0.158655.

Note that in Excel you can do this in two cells. First find the area to the left of 69.5 by using =NORM.DIST(69.5,67,2.5,TRUE) and the value 0.8413 is returned. In a new cell then subtract this value from 1 to get the answer 0.1587.

In 2009, the average SAT mathematics score was 501, with a standard deviation of 116. If we randomly selected a student from that year who took the SAT, what is the probability of getting a SAT mathematics score between 400 and 600?

Solution

Find P(400 ≤ X ≤ 600) using the TI calculator normalcdf(400,600,501,116) = 0.6113, which is also close to our results above. In Excel we can use the following formula =NORM.DIST(600,501,116,TRUE)- NORM.DIST(400,501,116,TRUE). Note that the right-hand endpoint goes in first. If you put the 400 in first you would get a negative answer, and probabilities are never negative. You can also do each piece separately in two cells, then in a third cell subtract the smaller area from the larger area.

A nice feature of this section is that the problems will say that the distribution is normally distributed, unlike the discrete distributions where you have to look for certain characteristics. However, when handling real data, you may have to know how to detect whether the data is normally distributed. One way to see if your variable is approximately normally distributed is by looking at a histogram, or we can use a normal probability plot.

6.4.3 Normal Probability Plot

A normal quantile plot, also called a normal probability plot, is a graph that is useful in assessing normality. A normal quantile plot plots the variable x against each of the x values corresponding z-score. It is not practical to make a normal quantile plot by hand.

Interpreting a normal quantile plot to see if a distribution is approximately normally distributed.

1. All of the points should lie roughly on a straight line y = x.
2. There should be no S pattern present.
3. Outliers appear as points that are far away from the overall pattern of the plot.

Here are two examples of histograms with their corresponding quantile plots. Note that as the distribution becomes closer to a normal distribution the dots on the quantile plot will be in a straighter line. Figures 6-21 is the histogram and figure 6-22 is the corresponding normal probability plot. Note the histogram is skewed to the left and dots do not line up on the y = x line. Figures 6-23 and Figure 6-24 represent a sample that is approximately normally distributed. Note that the dots still do not line up perfectly on the line y = x, but they are close to the line.

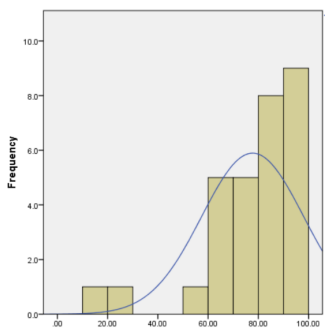
Figure 6-21

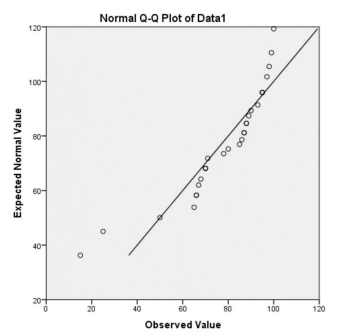
Figure 6-22

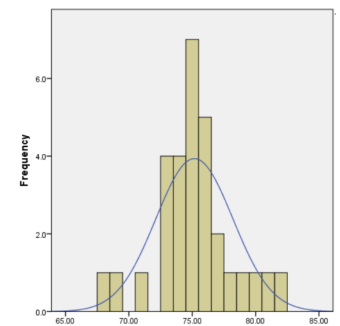
Figure 6-23

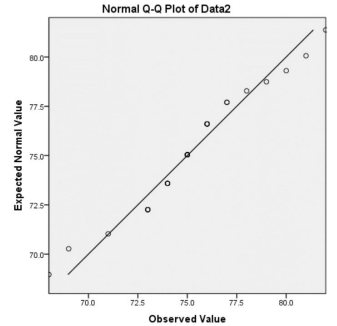
Figure 6-24

6.4.4 Finding Percentiles for a Normal Distribution

Sometimes you will be given an area or probability and have to find the associated random variable x or z-score. For example, the probability below a point on the normal distribution is a percentile. If we find that the P(Z < 1.645) =NORM.S.DIST(1.645,TRUE) = 0.950015, that tells us that about 95% of z-scores are below 1.645. In other words, the z-score of 1.645 is the 95^th percentile.

We can use technology to find z-score given a percentile. Most technology has built in commands that will find the probability below a point. If you want to find the area above a point, or between two points, then find the area below a point by using the complement rule and keep in mind that the total area under the curve is 1 and the total area below the mean is 0.5.

If x is an observation from a distribution that has mean μ and standard deviation σ, the standardized value of x (or zscore) is \(z=\frac{x-\mu}{\sigma}\).

If you have a z-score and want to convert back to x, you can do so by solving the above equation for x, which yields x = zσ + μ.

TI-84: Press [2nd] [DISTR]. This will get you a menu of probability distributions. Press 3 or arrow down to 3:invNorm( and press [ENTER]. This puts invNorm( on the home screen. Enter the area to the left of the x value, μ, and σ with a comma between each. Press [ENTER]. This will return the percentile for the x value. For example, to find the 95th percentile when the mean is 100 and the standard deviation is 20, you should have invNorm(0.95,100,20). If you leave out the μ and σ, then the default is the z-score for the standard normal distribution

TI-89: Go to the [Apps] Stat/List Editor, then select F5 [DISTR]. This will get you a menu of probability distributions. Arrow down to Inverse Normal and press [ENTER]. Enter the area to the left of the x value, μ, and σ into each cell. Press [ENTER]. This will return the percentile for the x value. For example, to find the 95th percentile when the mean is 100 and the standard deviation is 20, you should enter 0.95, 100, 20.

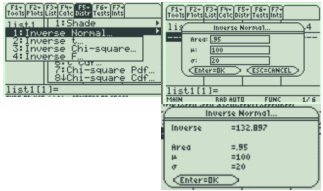
If you use μ = 0 and σ = 1, then the default is the z-score for the standard normal distribution.

Compute the z-score that corresponds to the 25^th percentile.

Solution

First, draw the standard normal curve with zero in the middle as in Figure 6-25. The 25th percentile would have to be below the mean since the mean = median = 50th percentile for a bell-shaped distribution.

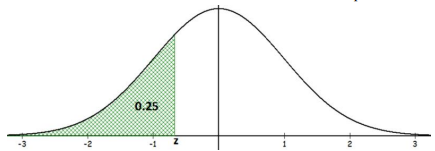
Figure 6-25

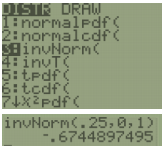
It is okay if you do not have this drawing to scale, but drawing a picture similar to Figure 6-25 will give you a good idea if your answer is correct. For instance, by just looking at this graph we can see that the answer for the z-score will need to be a negative number.

TI Calculator: z = invNorm(0.25,0,1) = -0.6745.

Excel: z = NORM.S.INV(0.25) = -0.6745.

The z = -0.6745 represents the 25^th percentile.

Compute the z-score that corresponds to the area of 0.4066 between zero and z shown in Figure 6-26.

Solution

First notice that this picture does not quite match the calculator or Excel, which will only find for a left-tail area. The value of zero is the median on a standard normal distribution, so 50% of the area lies to the left of z = 0. This means that the total area to the left of the unknown z-score would be 0.5 + 0.4066 = 0.9066.

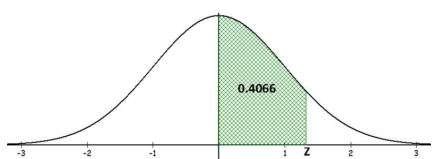
Figure 6-26

TI Calculator: z = invNorm(0.9066) = 1.32.

Excel: z = NORM.S.INV(0.9066) = 1.32.

Using Excel or TI-Calculator for the Percentile of a Normal Distribution

Note that the NORM.S.INV function is for a standard normal when µ = 0 and σ = 1.

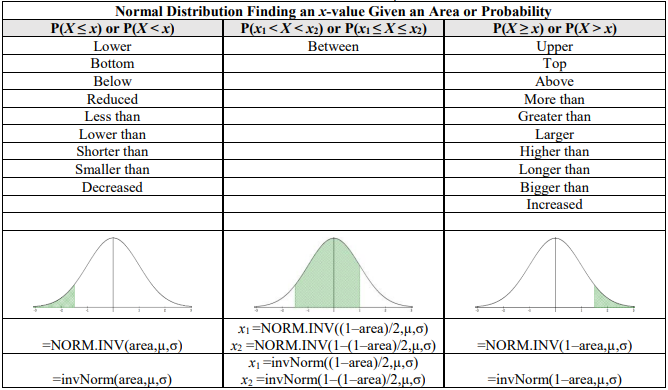
Figure 6-27

In 2009, the average SAT mathematics score was 501, with a standard deviation of 116. Find the SAT score that is for the top 10% of students taking the exam that year.

Solution

Draw the distribution curve and shade the top 10% as shown in Figure 6- 28. The area below the unknown x value in Figure 6-28 is 1 – 0.10 = 0.90.

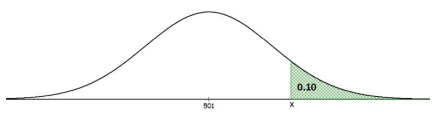
Figure 6-28

TI Calculator: invNorm(0.9,501,116) = 649.66.

Excel: =NORM.INV(0.9,501,116) = 649.66.

A student that scored above 649.66 would be in the top 10%, also known as the 90^th percentile.

We could have also found the z-score that corresponds to the top 10%. Then use the z-score formula to find the xvalue. Using Excel =NORM.S.INV(0.9) = 1.2816. Then use the formula x = zσ + μ = 1.2816 ∙ 116 + 501 = 649.67. This is using a rounded z-score so the answer is slightly off, but close.

Note: It is common practice to round z-scores to two decimal places. This is left over from using probability tables that only went out to two decimal places. If you use a rounded z-score in other calculations then keep in mind that you will get a larger rounding error.

If the average price of a new one family home is $246,300 with a standard deviation of $15,000, find the minimum and maximum prices of the houses that a contractor will build to satisfy the middle 98% of the market. Assume that the variable is normally distributed.

Solution

First, draw the curve and shade the middle area of 0.98, see Figure 6-29. We need to get the area to the left of the x₁ value. Take the complement 1 – 0.98 = 0.02, then split this area between both tails.

The lower tail area for x1 would have 0.02/2 = 0.01. The upper value of x₂ will have a left tail area of 0.99.

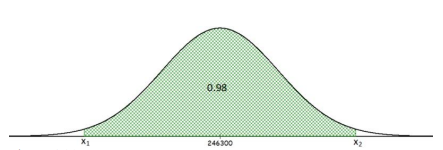
Figure 6-29

On the calculator use, invNorm(0.01,246300,15000) and you get a minimum price of $211404.78 and use invNorm(0.99,246300,15000) and you get a maximum price of $281195.22.

In Excel you would have to do this in two separate cells =NORM.INV(0.01,246300,15000) = $211,404.78 and =NORM.INV(0.99,246300,15000) = $281,195.22.