4.4: Union and Intersection
- Page ID
- 24036
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)When two events cannot happen at the same time, they are called mutually exclusive or disjoint events.
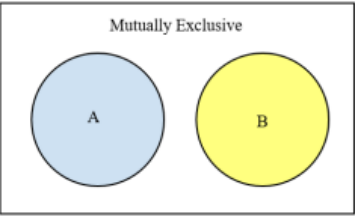
Figure 4-7
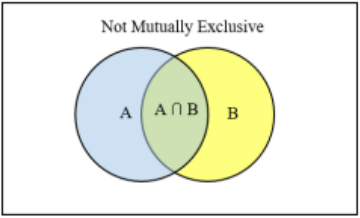
Figure 4-8
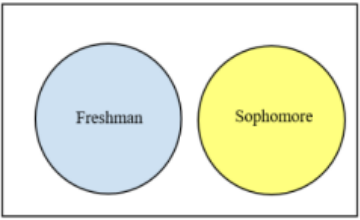
Figure 4-9
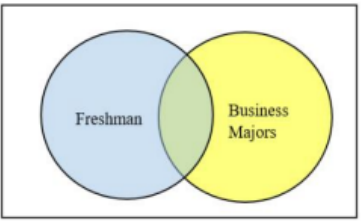
Figure 4-10
For example, a student cannot be a freshman and a sophomore at the same time, see Figure 4-9. These are mutually exclusive events. A student could be freshman and a business major at the same time so the event freshman and the event business major are not mutually exclusive see Figure 4-10.
Intersection
When we are finding the probability of both A and B happening at the same time we denote this as P(A ∩ B). This overlap is called the intersection.
When two events, say A and B, occur at the same time, this is denoted as the intersection of A and B and is denoted as (A ∩ B). Think of the symbol ∩ as an A in “and.”
If two events are mutually exclusive then A ∩ B = { } the empty set (also denoted as \(\varnothing\)) and the P(A ∩ B) = 0.
Union
When either event A, event B, or both occur then we call this the union of A or B, which is denoted as (A U B). When finding the probability of A or B we denote this as P(A U B). When we write “or” in statistics, we mean “and/or” unless we explicitly state otherwise. Thus, A or B occurs means A, B, or both A and B occur.
Figure 4-11 is a Venn diagram for the union rule.
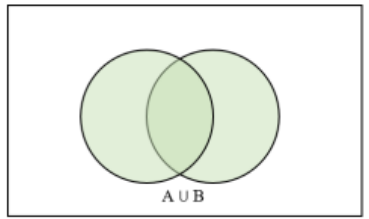
Figure 4-11
The Union Rule: P(A U B) = P(A) + P(B) – P(A ∩ B).
If two events are mutually exclusive, then the probability of them occurring at the same time is P(A ∩ B) = 0. So, if A and B are mutually exclusive then the P(A U B) = P(A) + P(B) as shown in Figure 4-7. It is best to write out the rule with the intersection so that you do not forget to subtract any overlapping intersection.
The family college data set contains a sample of 792 cases with two variables, teen and parents. The teen variable is either college or not, where the college label means the teen went to college immediately after high school. The parent’s variable takes the value degree if at least one parent of the teenager completed a college degree. Make a Venn Diagram for the data.
Example from OpenIntroStatistics.
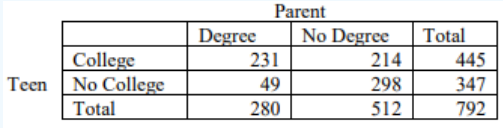
Solution
Find the relative frequencies.
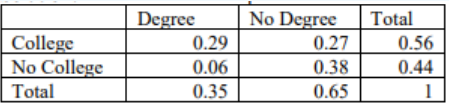
Figure 4-12 for completed Venn Diagram. Note that you do not need to use circles to represent the sets.
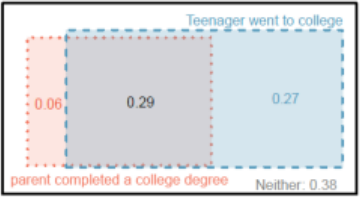
Figure 4-12
A random sample of 500 people was taken from the 2010 United States Census. Their marital status and race were recorded in the following contingency table using the census labels. A person is randomly chosen from the census data. Find the following.
Use a random experiment consisting of rolling two dice and adding the numbers on the faces.
a) Compute the probability of rolling a sum of 8.
b) Compute the probability of rolling a sum of 8 or a sum of 5
c) Compute the probability of rolling a sum of 8 or a double (each die has the same number).
Solution
a) There are 36 possible outcomes for rolling the two dice as shown in the following sum table. There are 5 pairs where the sum of the two dice is an 8, the (2,6), (3,5), (4,4), (5,3) and (6,2). Note that the events (2,6) and (6,2) are different outcomes since they numbers come from different dice.
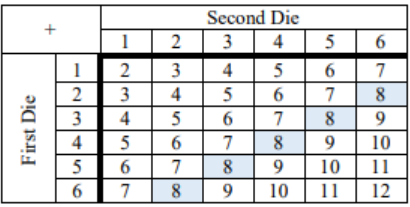
Thus, the P(8) = 5/36 = 0.1389.
b) Highlight all the places where a sum of 5 or a sum of 8 occurs. There are 9 pairs where the sum of the two dice is a 5 or an 8.
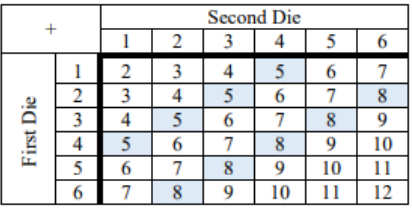
Thus, the P(5 U 8) = P(5) + P(8) – P(5 ∩ 8) = 4/36 + 5/36 – 0 = 9/36 = 0.25.
Note that rolling a sum of 5 is mutually exclusive from rolling a sum of 8 so the probability is zero for the intersection of the two events.
c) The events rolling an 8 and rolling doubles are not mutually exclusive since the pair of fours (4, 4) falls into both events.
An easy way is to highlight all the places a sum 8 or doubles occur, count the highlighted values, and divide by the total 10/36 = 0.2778.
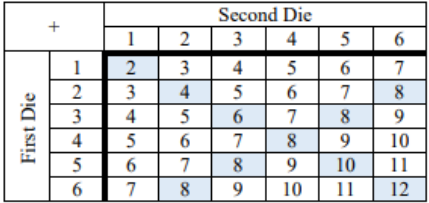
When using the union rule, we subtract this overlap out one time to account for this. Using the union formula:
P(8 U Doubles) = P(8) + P(Doubles) – P(8 ∩ Doubles) = 5/36 + 6/36 – 1/36 = 10/36 = 0.2778.
“‘It's... well, it's a long story,’ he said, ‘but the Question I would like to know is the Ultimate Question of Life, the Universe and Everything. All we know is that the Answer is Forty-two, which is a little aggravating.’
Prak nodded again.
‘Forty-two,’ he said. ‘Yes, that's right.’
He paused. Shadows of thought and memory crossed his face like the shadows of clouds crossing the land.
‘I'm afraid,’ he said at last, ‘that the Question and the Answer are mutually exclusive. Knowledge of one logically precludes knowledge of the other. It is impossible that both can ever be known about the same universe.’”
(Adams, 2002)
Randomly pick a card from a standard deck. A standard deck of cards, not including jokers consists of 4 suits called clubs = ♣, spades = ♠, hearts = ♥, and diamonds = ♦. The clubs and spades are called the black cards. The hearts and diamonds are called the red cards. Each suit has 13 cards. The numbered cards shown in Figure 4-13, are Ace = 1 or A, 2, 3, 4, 5, 6, 7, 8, 9, 10. The face cards are the Jack = J, Queen = Q, and King = K.

Figure 4-13
a) Compute the probability of selecting a card that shows a club.
b) Compute the probability of selecting a heart or a spade card.
c) Compute the probability of selecting a spade or a face card.
Solution
a) There are 52 cards in a standard deck. There are 13 cards of each suit. The P(♣) = 13/52 = 0.25.
b) There are 52 cards in a standard deck. There are 13 cards of each suit. P(♥ U ♠) = 26/52 = 0.5.
c) There are 13 spades and 12 face cards. However, there are 3 cards that are both spades and face cards. P(♠ U FC) = P(♠) + P(FC) – P(♠ ∩ FC) = 13/52 + 12/52 – 3/52 = 22/52 = 0.4231. Since the sample space is small, you could just count how many spades and face cards there are.

Words Are Important!
When working with probability, words such as “more than” or “less than” can drastically change the answer. Figure 4-14 shows some of the common phrases you may run into while reading a problem. It will be essential later in the course that you can correctly match these phrases with their correct symbol.
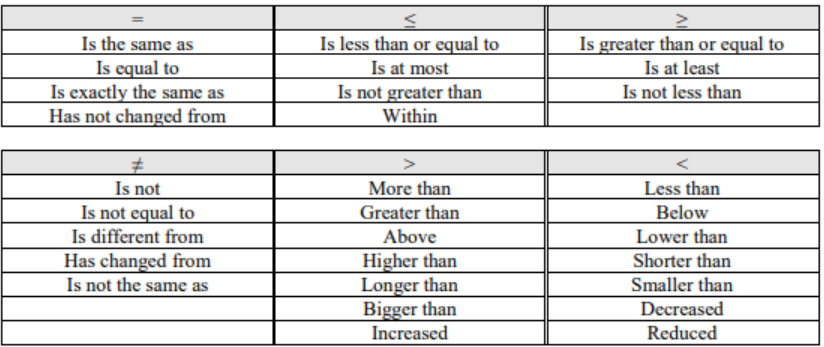
Figure 4-14
Use a random experiment consisting of rolling two dice and adding the numbers on the faces.
a) Compute the probability of rolling a sum of less than 5.
b) Compute the probability of rolling a sum of 5 or less.
Solution
a) Let X be the event rolling a sum less than 5. A sum less than 5 would not include the 5. For notation, we use P(X < 5), which is read as the “probability that X is less than five.” Shade in all the sums that are less than 5.
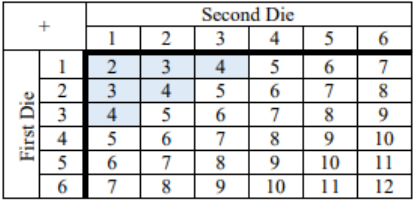
Then the P(X < 5) = 6/36 = 0.1667.
b) : Let X be the event rolling a sum of 5 or less. A sum of 5 or less includes the 5. For notation, we can use P(X ≤ 5), which is read as the “probability that X is less than or equal to five.” Shade in all the sums that are 5 or less.
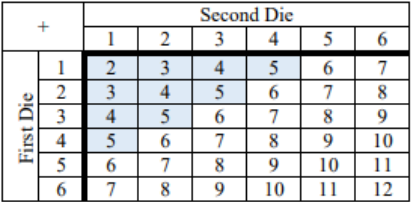
Then the P(X ≤ 5) = 10/36 = 0.2778.


