Unit 4A: Introduction to Statistical Inference
- Page ID
- 31265
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)CO-1: Describe the roles biostatistics serves in the discipline of public health.
CO-6: Apply basic concepts of probability, random variation, and commonly used statistical probability distributions.
Review: We are about to move into the inference component of the course and it is a good time to be sure you understand the basic ideas presented regarding exploratory data analysis.
Video: Unit 4A: Introduction to Statistical Inference (15:45)
Recall again the Big Picture, the four-step process that encompasses statistics: data production, exploratory data analysis, probability and inference.
We are about to start the fourth and final unit of this course, where we draw on principles learned in the other units (Exploratory Data Analysis, Producing Data, and Probability) in order to accomplish what has been our ultimate goal all along: use a sample to infer (or draw conclusions) about the population from which it was drawn.
As you will see in the introduction, the specific form of inference called for depends on the type of variables involved — either a single categorical or quantitative variable, or a combination of two variables whose relationship is of interest.
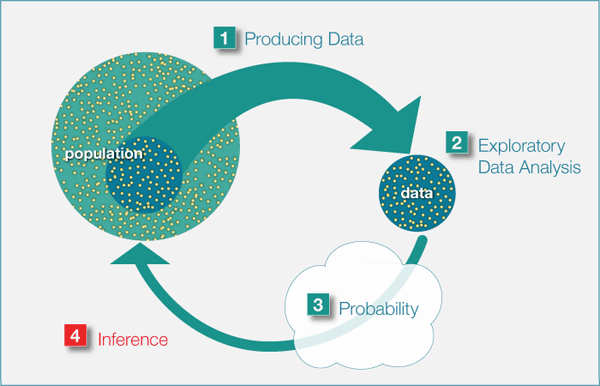
Introduction
LO 6.23: Explain how the concepts covered in Units 1 – 3 provide the basis for statistical inference.
We are about to start the fourth and final part of this course — statistical inference, where we draw conclusions about a population based on the data obtained from a sample chosen from it.
The purpose of this introduction is to review how we got here and how the previous units fit together to allow us to make reliable inferences. Also, we will introduce the various forms of statistical inference that will be discussed in this unit, and give a general outline of how this unit is organized.
In the Exploratory Data Analysis unit, we learned to display and summarize data that were obtained from a sample. Regardless of whether we had one variable and we examined its distribution, or whether we had two variables and we examined the relationship between them, it was always understood that these summaries applied only to the data at hand; we did not attempt to make claims about the larger population from which the data were obtained.
Such generalizations were, however, a long-term goal from the very beginning of the course. For this reason, in the unit on Producing Data, we took care to establish principles of sampling and study design that would be essential in order for us to claim that, to some extent, what is true for the sample should be also true for the larger population from which the sample originated.
These principles should be kept in mind throughout this unit on statistical inference, since the results that we will obtain will not hold if there was bias in the sampling process, or flaws in the study design under which variables’ values were measured.
Perhaps the most important principle stressed in the Producing Data unit was that of randomization. Randomization is essential, not only because it prevents bias, but also because it permits us to rely on the laws of probability, which is the scientific study of random behavior.
In the Probability unit, we established basic laws for the behavior of random variables. We ultimately focused on two random variables of particular relevance: the sample mean (x-bar) and the sample proportion (p-hat), and the last section of the Probability unit was devoted to exploring their sampling distributions.
We learned what probability theory tells us to expect from the values of the sample mean and the sample proportion, given that the corresponding population parameters — the population mean (mu, μ) and the population proportion (p) — are known.
As we mentioned in that section, the value of such results is more theoretical than practical, since in real-life situations we seldom know what is true for the entire population. All we know is what we see in the sample, and we want to use this information to say something concrete about the larger population.
Probability theory has set the stage to accomplish this: learning what to expect from the value of the sample mean, given that population mean takes a certain value, teaches us (as we’ll soon learn) what to expect from the value of the unknown population mean, given that a particular value of the sample mean has been observed.
Similarly, since we have established how the sample proportion behaves relative to population proportion, we will now be able to turn this around and say something about the value of the population proportion, based on an observed sample proportion. This process — inferring something about the population based on what is measured in the sample — is (as you know) called statistical inference.
Types of Inference
LO: 1.9 Distinguish between situations using a point estimate, an interval estimate, or a hypothesis test.
We will introduce three forms of statistical inference in this unit, each one representing a different way of using the information obtained in the sample to draw conclusions about the population. These forms are:
- Point Estimation
- Interval Estimation
- Hypothesis Testing
Obviously, each one of these forms of inference will be discussed at length in this section, but it would be useful to get at least an intuitive sense of the nature of each of these inference forms, and the difference between them in terms of the types of conclusions they draw about the population based on the sample results.
Point Estimation
In point estimation, we estimate an unknown parameter using a single number that is calculated from the sample data.
Based on sample results, we estimate that p, the proportion of all U.S. adults who are in favor of stricter gun control, is 0.6.
Interval Estimation
In interval estimation, we estimate an unknown parameter using an interval of values that is likely to contain the true value of that parameter (and state how confident we are that this interval indeed captures the true value of the parameter).
Based on sample results, we are 95% confident that p, the proportion of all U.S. adults who are in favor of stricter gun control, is between 0.57 and 0.63.
Hypothesis Testing
In hypothesis testing, we begin with a claim about the population (we will call the null hypothesis), and we check whether or not the data obtained from the sample provide evidence AGAINST this claim.
It was claimed that among all U.S. adults, about half are in favor of stricter gun control and about half are against it. In a recent poll of a random sample of 1,200 U.S. adults, 60% were in favor of stricter gun control. This data, therefore, provides some evidence against the claim.
Soon we will determine the probability that we could have seen such a result (60% in favor) or more extreme IF in fact the true proportion of all U.S. adults who favor stricter gun control is actually 0.5 (the value in the claim the data attempts to refute).
It is claimed that among drivers 18-23 years of age (our population) there is no relationship between drunk driving and gender.
A roadside survey collected data from a random sample of 5,000 drivers and recorded their gender and whether they were drunk.
The collected data showed roughly the same percent of drunk drivers among males and among females. These data, therefore, do not give us any reason to reject the claim that there is no relationship between drunk driving and gender.
Did I Get This?: Types of Inference
In terms of organization, the Inference unit consists of two main parts: Inference for One Variable and Inference for Relationships between Two Variables. The organization of each of these parts will be discussed further as we proceed through the unit.
Inference for One Variable
The next two topics in the inference unit will deal with inference for one variable. Recall that in the Exploratory Data Analysis (EDA) unit, when we learned about summarizing the data obtained from one variable where we learned about examining distributions, we distinguished between two cases; categorical data and quantitative data.
We will make a similar distinction here in the inference unit. In the EDA unit, the type of variable determined the displays and numerical measures we used to summarize the data. In Inference, the type of variable of interest (categorical or quantitative) will determine what population parameter is of interest.
- When the variable of interest is categorical, the population parameter that we will infer about is the population proportion (p) associated with that variable. For example, if we are interested in studying opinions about the death penalty among U.S. adults, and thus our variable of interest is “death penalty (in favor/against),” we’ll choose a sample of U.S. adults and use the collected data to make an inference about p, the proportion of U.S. adults who support the death penalty.
- When the variable of interest is quantitative, the population parameter that we infer about is the population mean (mu, µ) associated with that variable. For example, if we are interested in studying the annual salaries in the population of teachers in a certain state, we’ll choose a sample from that population and use the collected salary data to make an inference about µ, the mean annual salary of all teachers in that state.
The following outlines describe some of the important points about the process of inferential statistics as well as compare and contrast how researchers and statisticians approach this process.
Outline of Process of Inference
Here is another restatement of the big picture of statistical inference as it pertains to the two simple examples we will discuss first.
- A simple random sample is taken from a population of interest.
- In order to estimate a population parameter, a statistic is calculated from the sample. For example:
Sample mean (x-bar)
Sample proportion (p-hat)
- We then learn about the DISTRIBUTION of this statistic in repeated sampling (theoretically). We now know these are called sampling distributions!
- Using THIS sampling distribution we can make inferences about our population parameter based upon our sample statistic.
It is this last step of statistical inference that we are interested in discussing now.
Applied Steps (What do researchers do?)
One issue for students is that the theoretical process of statistical inference is only a small part of the applied steps in a research project. Previously, in our discussion of the role of biostatistics, we defined these steps to be:
- Planning/design of study
- Data collection
- Data analysis
- Presentation
- Interpretation
You can see that:
- Both exploratory data analysis and inferential methods will fall into the category of “Data Analysis” in our previous list.
- Probability is hiding in the applied steps in the form of probability sampling plans, estimation of desired probabilities, and sampling distributions.
Among researchers, the following represent some of the important questions to address when conducting a study.
- What is the population of interest?
- What is the question or statistical problem?
- How to sample to best address the question given the available resources?
- How to analyze the data?
- How to report the results?
AFTER you know what you are going to do, then you can begin collecting data!
Theoretical Steps (What do statisticians do?)
Statisticians, on the other hand, need to ask questions like these:
- What assumptions can be reasonably made about the population?
- What parameter(s) in the population do we need to estimate in order to address the research question?
- What statistic(s) from our sample data can be used to estimate the unknown parameter(s)?
- How does each statistic behave?
- Is it unbiased?
- How variable will it be for the planned sample size?
- What is the distribution of this statistic? (Sampling Distribution)
Then, we will see that we can use the sampling distribution of a statistic to:
- Provide confidence interval estimates for the corresponding parameter.
- Conduct hypothesis tests about the corresponding parameter.
Standard Error of a Statistic
LO: 1.10: Define the standard error of a statistic precisely and relate it to the concept of the sampling distribution of a statistic.
In our discussion of sampling distributions, we discussed the variability of sample statistics; here is a quick review of this general concept and a formal definition of the standard error of a statistic.
- All statistics calculated from samples are random variables.
- The distribution of a statistic (from a sample of a given sample size) is called the sampling distribution of the statistic.
- The standard deviation of the sampling distribution of a particular statistic is called the standard error of the statistic and measures variability of the statistic for a particular sample size.
The standard error of a statistic is the standard deviation of the sampling distribution of that statistic, where the sampling distribution is defined as the distribution of a particular statistic in repeated sampling.
- The standard error is an extremely common measure of the variability of a sample statistic.
In our discussion of sampling distributions, we looked at a situation involving a random sample of 100 students taken from the population of all part-time students in the United States, for which the overall proportion of females is 0.6. Here we have a categorical variable of interest, gender.
We determined that the distribution of all possible values of p-hat (that we could obtain for repeated simple random samples of this size from this population) has mean p = 0.6 and standard deviation
\(\sigma_{\hat{p}}=\sqrt{\dfrac{p(1-p)}{n}}=\sqrt{\dfrac{0.6(1-0.6)}{100}}=0.05\)
which we have now learned is more formally called the standard error of p-hat. In this case, the true standard error of p-hat will be 0.05.
We also showed how we can use this information along with information about the center (mean or expected value) to calculate probabilities associated with particular values of p-hat. For example, what is the probability that sample proportion p-hat is less than or equal to 0.56? After verifying the sample size requirements are reasonable, we can use a normal distribution to approximate
\(P(\hat{p} \leq 0.56)=P\left(Z \leq \dfrac{0.56-0.6}{0.05}\right)=P(Z \leq-0.80)=0.2119\)
Similarly, for a quantitative variable, we looked at an example of household size in the United States which has a mean of 2.6 people and standard deviation of 1.4 people.
If we consider taking a simple random sample of 100 households, we found that the distribution of sample means (x-bar) is approximately normal for a large sample size such as n = 100.
The sampling distribution of x-bar has a mean which is the same as the population mean, 2.6, and its standard deviation is the population standard deviation divided by the square root of the sample size:
\(\dfrac{\sigma}{\sqrt{n}}=\dfrac{1.4}{\sqrt{100}}=0.14\)
Again, this standard deviation of the sampling distribution of x-bar is more commonly called the standard error of x-bar, in this case 0.14. And we can use this information (the center and spread of the sampling distribution) to find probabilities involving particular values of x-bar.
\(P(\bar{x}>3)=P\left(Z>\dfrac{3-2.6}{\dfrac{1.4}{\sqrt{100}}}\right)=P(Z>2.86)=0.0021\)

