5.2.1: Nested Model in SAS

Last updated
Save as PDF

Page ID: 33639

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Here is the SAS code to run the ANOVA model for the hours of exercise for high school students example discussed in lesson 5.2:

data Nested_Example_data;
infile datalines delimiter=',';
input Region $ City $ ExHours;
datalines;
    NE,NY,30
    NE,NY,35
    NE,Pittsburgh,18
    NE,Pittsburgh,20
    MW,Chicago,10
    MW,Chicago,9
    MW,Detroit,20
    MW,Detroit,22
    W,LA,18
    W,LA,19
    W,Seattle,4
    W,Seattle,6
;

/*to run the nested ANOVA model*/
proc mixed data=Nested_Example_data method=type3;
    class Region City;
    model ExHours = Region City(Region);
    store nested1;
run;

/*to obtain the resulting multiple comparison results*/
ods graphics on;
proc plm restore=nested1;
    lsmeans Region / adjust=tukey plot=meanplot cl lines;
    lsmeans City(Region) / adjust=tukey plot=meanplot cl lines;
run;

When we run this SAS program, here is the output that we are interested in:

Type 3 Analysis of Variance
Source	DF	Sum of Squares	Mean Square	Expected Mean Square	Error Term	Error DF	F Value	Pr > F
Region	2	424.666667	212.333333	Var(Residual)+Q(Region, City(Region))	MS(Residual)	6	65.33	<.0001
City(Region)	3	496.750000	165.583333	Var(Residual)+Q(City(Region))	MS(Residual)	6	50.95	0.0001
Residual	6	19.500000	3.250000	Var(Residual)

Type 3 Test of Fixed Effects
Effect	Num DF	Den DF	F Value	Pr>F
Region	2	6	65.33	<.0001
City(Region)	3	6	50.95	0.0001

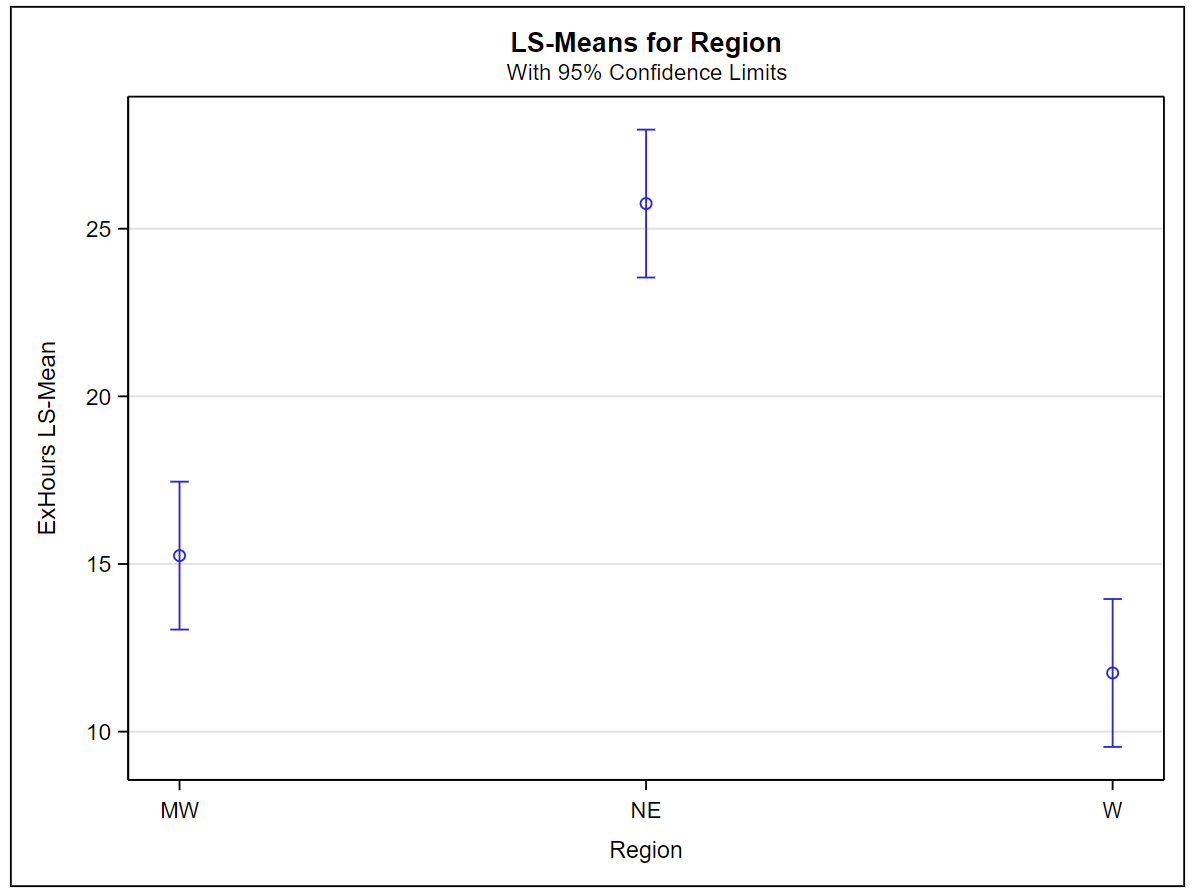
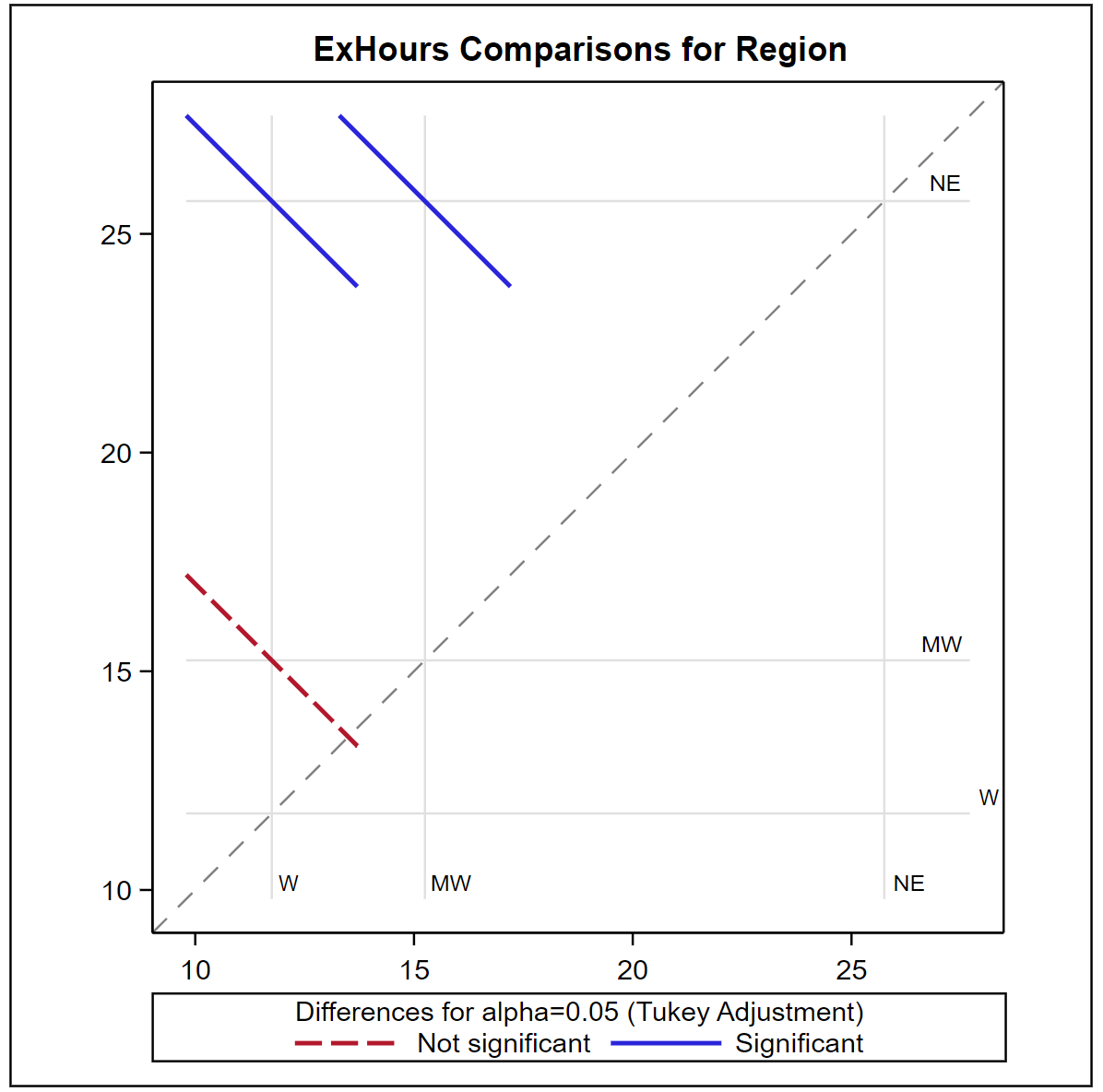
The \(p\)-values above indicate that both Region and City(Region) are statistically significant. The plots and charts below obtained from the Tukey option specify the means which are significantly different.

Graph of exercise hours LS-mean vs region, with 95% confidence limits. — Figure \(\PageIndex{1}\): Mean hours of exercise by Region with 95% CIs

Diffogram of exercise hours comparisons for region. — Figure \(\PageIndex{2}\): Diffogram for Mean Comparisons by Region

Graph of exercise hours LS-mean for city(region), with 95% confidence limits. — Figure \(\PageIndex{3}\): Mean hours of exercise by City(Region) with 95% CIs

Diffogram of exercise hours comparisons for city(region) — Figure \(\PageIndex{4}\): Diffogram for Mean Comparisons by City(Region)

The exercise hours on average are statistically higher in the northeastern region compared to the midwest and the west while the average exercise hours of these two regions are not significantly different.

Also, the comparison of the means between cities indicates that the high schoolers in New York city exercise significantly more than the other cities in the study. The exercise levels are similar among Detroit, Pittsburgh, and LA, while exercise levels of high schoolers in Chicago and Seattle are similar but significantly lower than all other cities in the study.

These grouping observations are further confirmed by the lines plots below.

Line plot for multiple comparisons of means for Regions. Region NE is covered by a blue bar, and regions MW and W are covered by a single red bar. — Figure \(\PageIndex{5}\): Line plot for multiple comparisons of means for Regions.

Line plot for multiple comparisons of means for Cities. NY in region NE is covered by a single blue bar. Detroit in region MW, Pittsburg in region NE, and LA in region W are covered by a single red bar. Chicago in region MW and Seattle in region W are covered by a single green bar. — Figure \(\PageIndex{6}\): Line plot for multiple comparisons of means for Cities.