3.5.1: Graphs and Properties of Logarithmic Functions (Exercises)
- Page ID
- 26516
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)
SECTION 5.5 PROBLEM SET: GRAPHS AND PROPERTIES OF LOGARITHMIC FUNCTIONS
Questions 1 – 3: For each of the following functions
- Sketch a reasonably accurate graph showing the shape of the graph of the function
- State the domain
- State the range
- State whether the graph has a vertical asymptote or a horizontal asymptote and write the equation of that asymptote
- Does the graph have an x-intercept or a y-intercept asymptote? Write the coordinates of the x-intercept or the y-intercept.
|
|
|
|
|
|
Questions 4 - 5: For the pair of inverse functions \(y = e^x\) and \(y = \ln x\)
- Sketch a reasonably accurate graph showing the shape of the graph of the function
- State the domain
- State the range
- State whether the graph has a vertical asymptote or a horizontal asymptote and write the equation of that asymptote
- Does the graph have an x-intercept or a y-intercept asymptote? Write the coordinates of the xintercept or the y-intercept.
|
|
|
|
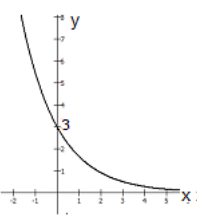
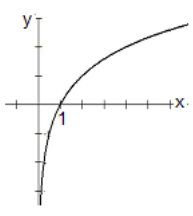
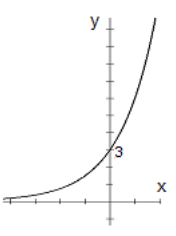
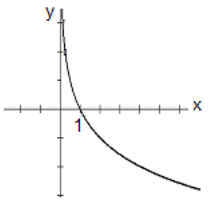
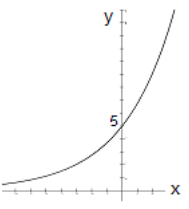
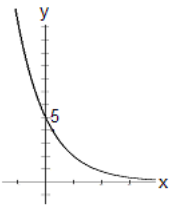
Questions 6-11: Match the graph with the function.
Choose the function from the list below and write it on the line underneath the graph.
Hint: To match the function and the graph, identify these properties of the graph and function
- Is the function increasing decreasing?
- Examine the asymptote
- Determine the x or y intercept
\[\mathrm{y}=3\left(2^{x}\right) \quad y=5\left(0.4^{x}\right) \quad y=\log _{2}(x) \quad y=\log _{1 / 2}(x) \quad y=3 e^{-0.6 x} \quad y=5 e^{0.3 x} \nonumber \]
|
|
|
|
|
|