3.6: Counting

17

Counting

jkesler

We have seen that many situations call for a the Classical Approach when calculating probabilities; that is $P(A) = \frac{ \text{ number of ways } A \text{ can occur}}{\text{ number of different simple events}}$.

For example, if we are asked to calculate the probability of a sum of 3 when rolling two dice, the number of ways a 3 can occur is a simple calculation: you could get a 1 on the first die and a 2 on the second die, or you can get a 2 on the first die and a 1 on the second. To calculate the number of different simple events in the sample space, we can list all possibilities for rolling two dice:

First	Second
1	1
1	2
1	3
1	4
1	5
1	6

First	Second
2	1
2	2
2	3
2	4
2	5
2	6

First	Second
3	1
3	2
3	3
3	4
3	5
3	6

 

First	Second
4	1
4	2
4	3
4	4
4	5
4	6

First	Second
5	1
5	2
5	3
5	4
5	5
5	6

First	Second
6	1
6	2
6	3
6	4
6	5
6	6

There are 36 different possible simple events when rolling two dice, so the probability of getting a sum of three is $\frac{2}{36} \approx 0.0556 $
A challenge arises, however, when either the numerator or the denominator (or both) is a large number. For example, if we wanted to know what the probability is of someone randomly guessing your social security number (SSN), we can use the classical approach.

$P(\text{guessing your SSN})=\frac{\text{how many SSN’s you have}}{\text{number of possible SSN’s}}$

You only have one SSN, so the numerator is 1. To find the denominator, if we try to list out all possible SSN’s as we did in the dice example above, we will be writing for a very long time because, as we will see, there are about a billion different possible SSN’s a person could randomly choose from.

1. Multiplication Counting Rule

The multiplication counting rule says that if there are $m$ possible outcomes for one procedure, and there are $n$ possible outcomes for another procedure, then there are $m\cdot n$ possible outcomes if both procedures are performed together.

Example: Dice and Coin Flips

Suppose in one procedure has you rolling a die and recording the number it lands on, and another procedure has you flipping a quarter and recording whether it lands heads or tails.

The first procedure has 6 possible outcomes (1, 2, 3, 4, 5 or 6), and the second procedure has 2 possible outcomes (heads or tails), so there are $6 \cdot 2 = 12$ possible outcomes for rolling a die and flipping a quarter.

I will list all 12 ways out for clarity, but keep in mind that the purpose of these counting rules is that we can count without having to list everything out. Here is the list of all 12 possible outcomes:

1, heads	4, heads	1, tails	4, tails
2, heads	5, heads	2, tails	5, tails
3, heads	6, heads	3, tails	6, tails

 

Example: License Plate

In California, pickup trucks have license plates that are formatted as follows: digit, letter, digit, digit, digit, digit, digit. For example, a truck may have the license plate 7X74293. However, 8RCB329 would a license plate you could see on a sedan, not a truck.

Suppose we are creating the very first truck license plate with this scheme. What is the probability that a randomly created license plate for a pickup truck will start with the number 7?

Answer:
To solve this, we will use the Classical Approach to probability. We must first find the number of possible truck license plates that start with 7. Then we must find the number of possible truck license plates in total. Finally, the Classical Approach tells us to divide these.

To find the possible number licenses that start with 7, we note that there is only one way for a 7 to appear first, there are 26 possibilities for the next letter, there are 10 possibilities (0-9) for each of the next five spots on the license. So the number of license plates that start with 7 is $1\cdot 26 \cdot 10 \cdot 10 \cdot 10 \cdot 10 \cdot 10 =2,600,000$

To find the total possible number of license plates, we do a similar calculation as above, except this time there are 10 possibilities for the first spot since it doesn’t have to be a 7. There are $10\cdot 26 \cdot 10 \cdot 10 \cdot 10 \cdot 10 \cdot 10 =26,000,000$

Finally, the probability that the license plate will start with a 7 is $\frac{2,600,000}{26,000,000} = 0.1$

II. Factorial Rule

Factorial Notation

In mathematics, we use the exclamation mark “!” as what is called “factorial notation”. It means repeated multiplication by starting with a whole number and removing one each time.

$n! = n\cdot (n-1) \cdot (n-2) \cdot \ldots \cdot 3 \cdot 2 \cdot 1$

For example $6! = 6 \cdot 5 \cdot 4 \cdot 3 \cdot 2 \cdot 1 = 720$

The factorial rule says that if we have $n$ different items, then there are $n! $ ways of arranging them.

Example: Delivery Routes

Suppose there are 3 people, Sarah, Dave, and Ahmed, delivering packages for Amazon, Inc. When they show up for work in the morning, they are each assigned one of three possible routes; one route goes to Roseville, one route goes to Rocklin, and one goes to Sacramento. The Rocklin route is always preferred because it has the least amount of traffic, and the Sacramento route is the least preferred since it has the most traffic.

In how many ways can their boss assign them to the routes?

Answer:
Since there are 3 people to arrange into the different routes, there are $3! = 6$ different ways to assign each person to a route.

Again, one of the purposes of counting rules is to avoid making lists, but for clarity, we list the 6 ways here, with each row representing one way to assign them:

Roseville Route	Rocklin Route	Sacramento Route
Sarah	Dave	Ahmed
Sarah	Ahmed	Dave
Dave	Sarah	Ahmed
Dave	Ahmed	Sarah
Ahmed	Dave	Sarah
Ahmed	Sarah	Dave

Sheets: Factorials

To calculate a factorial using a spreadsheet, use the =FACT(n) formula. (read more)

For example, to calculate 11!, you can type into a cell =FACT(11) which evaluates to 39,916,800 which is 11!

III. Permutations Rule ($_nP_r$)

The Permutations Rule says that if you have $n$ distinct items, and you will choose $r$ of them (without replacement), then the following formula gives the number of ways to do that when order is important:

$$ _n P_r = \frac{n!}{(n-r)!}$$

Example: Order is Important

In some situations, the order that things are in when they are chosen is important, and in other situations, the order is not important.

In the next example, Who’s the Boss, we are choosing from a group of people where the first person we pick will be CEO, the second person we pick will be CFO and the third person will be coffee runner. Suppose we pick Yasameen first, Jayde second, and De’Ana third. That will be different from if we pick De’Ana first, Jayde second, and Yasameen third, because their positions in the company would be different. So order matters in this case.

Suppose we had a box with 10 different colored scarves, and we are picking 3. If we don’t care about order, then picking Red, then Green, then Blue would be the same as picking Green, then Blue, then Red, and we would not count those as two different combinations. In this case, this is not what we call counting permutations, but what we will call counting combinations, and we deal with those below in section IV. Combinations.

 

Important Note

One thing to keep in mind about permutations is that the order of the items matters. For example, if you are permuting 3 letters, ABC would count as one permutation, BAC would count as another, and CBA would count as another.

We will address the situation where the order of the items doesn’t matter when we talk about combinations below.

Example: Who’s the Boss

You’ve just started your new company writing gaming apps for mobile phones. You have five friends, Amanda, Beatrice, Chloe, Destiny, and Everett, who want to work for your company, but you only need a CEO, a CFO, and a coffee runner (you’re the programmer).

In how many ways can you choose from your 5 friends to fill the 3 positions?

Solution

Since we have 5 friends to choose from, we have $n=5$, and we have only 3 positions, so we will choose 3 of the 5 friends, so we have $r=3$.

$$_nP_r = _5P_3 = \frac{5!}{(5-3)!} = \frac{5\cdot 4\cdot 3\cdot 2\cdot 1}{2\cdot 1} = 5\cdot 4\cdot 3 = 60$$

There are 60 different ways to choose 3 friends from 5 people when order matters.

 

If the above result surprises you, try listing them all out. Start with five friends named A, B, C, D, & E. Now list out combinations of 3 of them and see if you can find all 60.
ABC
ABD
ABE
ACB (recall order matters, so ABC $\neq$ ACB)
ACD
. (find)
. (the)
. (rest)
Now that you’ve done that once, be glad that we have this new formula to count permutations, instead of having to list them all out to count them.

IV. Combinations Rule ($_nC_r$)

The Combinations Rule says that if you have $n$ distinct items, and you will choose $r$ of them (without replacement), then the following formula gives the number of ways to do that when order is not important:$$ _n C_r = \frac{n!}{(n-r)! \cdot r!}$$

Example: Digging Deeper

You need some help digging holes for replacement fence posts that blew down in the last wind storm. You offer to pay \$10/hour to any of your friends who can help. Unfortunately, 8 of your friends say they can do it, but you don’t have that kind of money. You decide that you only need 3 friends to help.

How many different ways can you choose 3 friends from the 8 who volunteered?

Solution

Since we have 8 friends to choose from, we have $n=8$, and we have only 3 positions, so we will choose 3 of the 8 friends, so we have $r=3$. Since order does not matter in this situation, we use the Combinations formula:

$$_nC_r = _8C_3 = \frac{8!}{(8-3)! (3)!} = \frac{8\cdot 7\cdot 6 \cdot 5\cdot 4\cdot 3\cdot 2\cdot 1}{(5\cdot 4\cdot 3\cdot 2\cdot 1) \cdot ( 3\cdot 2\cdot 1} = \frac{8\cdot 7\cdot 6}{ 3\cdot 2\cdot 1} = 8\cdot 7 = 56$$

There are 56 different ways to choose 3 friends from 8 people when order does not matter.

Sheets: Combinations & Permutations

To calculate a combination in most spreadsheet programs, use the function =COMBIN(n, r) (read more)

For example, to calculate $_8C_3$, you type into a cell =COMBIN(8,3) which would evaluate to 56.

To calculate a permutation, use the function =PERMUT(n,r) (read more)

For example, to calculate $_5P_3$, you type into a cell =PERMUT(5,3) which would evaluate to 60.

Key Takeaways

The reason for discussing methods of counting is that, in probability, we often need to know how many ways something could happen, and then use that information, along with the classical approach to probability, to calculate probabilities for events. Consider the following example. We need a way to count up the number of 11-letter combinations.

Example: Lots of Letters

What is the probability that if 11 capitalized (upper-case) letters are typed, no letters are repeated? (assume the order of the letters matters)

Solution

Let’s start by calling the event that we get 11 letters with no repeats event $A$. So we want to calculate $P(A)$, which is the probability that 11 capitalized letters have no repeats.

We need two pieces of information:

1. The number of 11 letter combinations that do not have two letters repeated (the order of the letters matter, so AB is different than BA)
2. The number of things that could happen in this situation; that is to say, the total number of 11 letter combinations with and without repeats.

To calculate the first item, the number of 11 letter combinations that do not have two letters repeated, recognize that this will follow the Permutation Rule, since we have 26 letters, we are choosing 11 of them (no repeats), and order matters. So we simply calculate $_{26}P_{11}$. Use the =PERMUT(26,11) function in Sheets.

$$_{26}P_{11} =308,403,583,488,000$$

So, the number of 11 letter combinations that do not have two letters repeated is 308,403,583,488,000.

To calculate the second thing, the total number of 11 letter combinations with and without repeats, notice that we have 26 choices for the first letter, 26 choices for the second, 26 choices for the third, etc, all the way to 26 choices for the 11^th letter. So this simply follows the Multiplication Counting Rule, and we simply need to multiply 26 to itself 11 times. You can use a spreadsheet to do this as well by typing =26^11

$$26^{11} = 3.67034E+15$$

The spreadsheet gives a strange looking number that ends with “E+15”. This is really just scientific notation that says move the decimal 15 places to the right. The problem is that $26^{11}$ is not 3,670,340,000,000,000 because the scientific notation has done some rounding. If you’re using Google Sheets on the website, to get the full number, click on the cell that has the scientific notation number, go to the Format menu, hover over Number, and in the menu that pops up, click Number 1,000.12

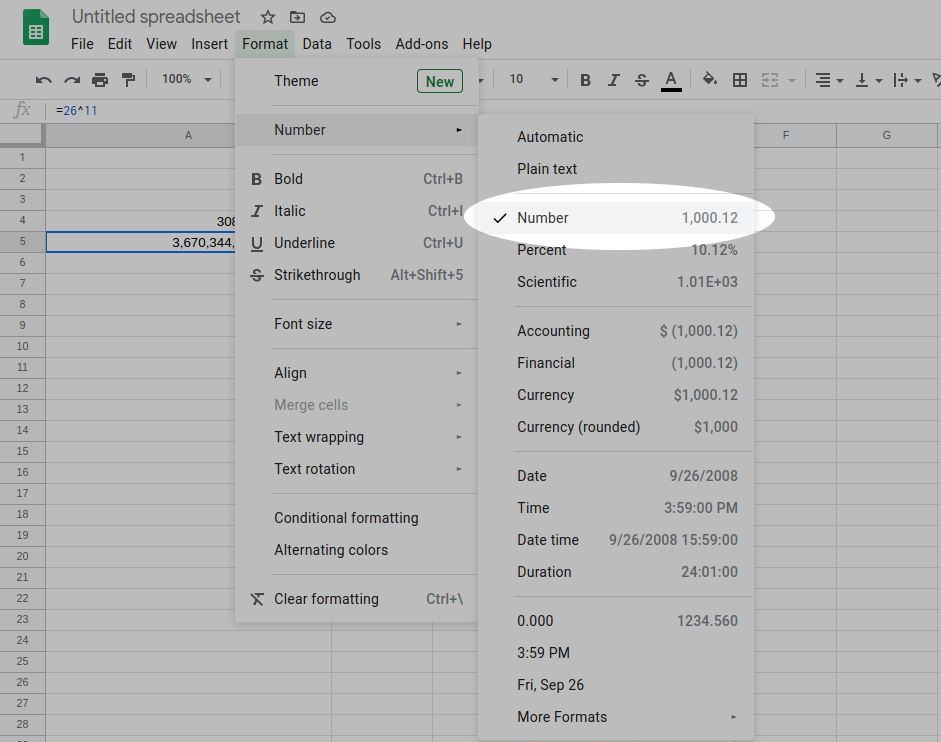
Now we see the following:

$$26^{11} = 3,670,344,486,987,780$$
Finally, the classical approach to probability says that we should divide the number of ways an event can happen (308,403,583,488,000 in this case) by the total number of things that could actually happen (3,670,344,486,987,780 in this case). We can do this in a spreadsheet easily. If the former value is in cell A1 and the latter value is in cell A2, then in another cell, we type =A1/A2 and find our answer.

$$P(A) = \frac{308,403,583,488,000}{3,670,344,486,987,780} = 0.084$$