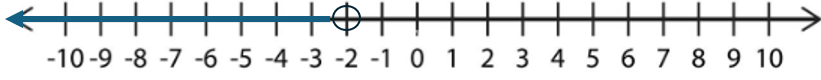Skip to main content
Statistics LibreTexts

2.4: Rational Inequalities

  1. Last updated
  2. Save as PDF
  • Page ID
    35206

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

    \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

    \( \newcommand{\dsum}{\displaystyle\sum\limits} \)

    \( \newcommand{\dint}{\displaystyle\int\limits} \)

    \( \newcommand{\dlim}{\displaystyle\lim\limits} \)

    \( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

    ( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

    \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

    \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

    \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

    \( \newcommand{\Span}{\mathrm{span}}\)

    \( \newcommand{\id}{\mathrm{id}}\)

    \( \newcommand{\Span}{\mathrm{span}}\)

    \( \newcommand{\kernel}{\mathrm{null}\,}\)

    \( \newcommand{\range}{\mathrm{range}\,}\)

    \( \newcommand{\RealPart}{\mathrm{Re}}\)

    \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

    \( \newcommand{\Argument}{\mathrm{Arg}}\)

    \( \newcommand{\norm}[1]{\| #1 \|}\)

    \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

    \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    \( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

    \( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

    \( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

    \( \newcommand{\vectorC}[1]{\textbf{#1}} \)

    \( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

    \( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

    \( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

    \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

    \(\newcommand{\longvect}{\overrightarrow}\)

    \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

    \(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)

    Solving rational inequalities involves finding the zeroes of the numerator and denominator, then using these values to investigate solution set regions on the number line.

    Example 2.4.1

    Solve the inequalities and write the solution sets in interval notation:

    1. \(\dfrac{x − 1}{x + 1} ≥ 0\)
    2. \(\dfrac{2x − 3}{x + 1} ≤ 0\)
    3. \(\dfrac{x + 2}{x − 2} ≥ 0\)
    Solution

    1. \(\dfrac{x - 1}{x + 1} ≥ 0\)
      Set x - 1 = 0 and solve 
      Add 1 to both sides
      x - 1 + 1 = 0 + 1
      x + 0 = 1
      x = 1
      Set x + 1 = 0 and solve
      Subtract 1 from both sides
      x + 1 - 1 = 0 - 1
      x + 0 = -1
      x = -1
      Since x = -1 will cause the rational expression to be undefined x cannot be equal to -1. 

      We have three regions, (-\(\infty\), -1), (-1, 1], and [1, \(\infty\)).  Let's look into each region.
      Select x = -2.

      \(\dfrac{-2 - 1}{-2 + 1} = \dfrac{-3}{-1} = 3\)
      Since it is positive, from negative infinity to -1 is a solution to the inequality (-\(\infty\), -1).  Let's now look in interval (-1, 1].

      Select x = 0
      \(\dfrac{0 - 1}{0 + 1} = \dfrac{-1}{1} < 0\)

      Since it is negative, (-1, 1] is not a solution to the inequality.

      \(\dfrac{2 - 1}{2 + 1} = \dfrac{1}{3} ≥ 0\)
      Since it is positive, [1, oo).

      (-\(\infty\), -1) U [1, \(\infty\)) is the 


       
    clipboard_ec6457b63e8b6cf693b68f135fe3dc0d3.png

    The zeroes divide the number line into 3 regions, x < −1, −1 < x < 1, x > 1

     

    1. \(\dfrac{2x − 3}{x + 1} ≤ 0\)

      Set the numerator and denominator equal to 0 and solve for x.
      2x - 3 = 0
      Add 3 to both sides
      2x - 3 + 3 = 0 + 3
      2x + 0 = 3
      2x = 3
      Divide by 2 on both sides
      \( x = \dfrac{3}{2}\)

      x + 1 = 0
      Subtract 1 from both sides
      x + 1 - 1 = 0 - 1
      x + 0 = -1
      x = -1

      There are three regions, x < -1, -1< x < 3/2, x > 3/2.

      In region x < -1, select x = -2.  Substitute in equation.
      \(\dfrac{2(-1)-3}{-2 + 1} = \dfrac{-5}{-1} = 5\)  
      Since the value is positive, it is not a solution for the inequality.

      In region -1 < x < 3/2, select x = 0.  Substitute in equation.
      \(\dfrac{2(0) - 3}{0 + 1} = \dfrac{-3}{1} = -3\)
      Since the value is negative, it is a solution for the inequality.

      In region x > 3/2, select x = 2.  Substitute in equation.
      \(\dfrac{2(2) - 3}{2 + 3} = \dfrac{1}{5}\)
      Since the value is positive, it is not a solution for the inequality.

      (-1, 3/2] is the solution for the inequality. 

       

    clipboard_ef09d3390915545992624d4a944327793.png

    The zeroes divide the number line into 3 regions, x < −1, −1 < x < 1.5, x > 1.5

     

     

    1. \(\dfrac{x + 2}{x − 2} ≥ 0 \)

      Set x + 2 and x - 2 equal to 0 and solve.
      x + 2 = 0
      Subtract 2 on both sides
      x + 2 - 2 = 0 - 2
      x + 0 = -2
      x = -2

      x - 2 = 0
      Add 2 to both sides
      x - 2 + 2 = 0 + 2
      x + 0 = 2
      x = 2

      There are three regions

      x < -2, -2 < x < 2, x > 2

      For the region x < -2, select a value x = -3.
      \(\dfrac{-3 + 2}{-3 - 2} = \dfrac{-1}{-1} = 1\)
      Since the value is position, this is a solution to the inequality.

      For the region -2 < x < 2, select a value x = 0.
      \(\dfrac{0 + 2}{0 - 2} = \dfrac{2}{-2} = -1\)
      Since the value is negative, this is not a solution.

      For the region x > 2, select a value x = 3.
      \(\dfrac{3 + 2}{3 - 2} = \dfrac{5}{1} = 5\)
      Since the value is positive, this is a solution to the inequality.

      The solution is (-\(\infty\), -2] U [2, \(\infty\)).

       

    clipboard_edd041a9d0b19f2643c86e437aab1b20d.png

    The zeroes divide the number line into 3 regions
     x < −2, −2 < x < 2, x > 2

     

     

    Exercise 2.4.1
    1. \(\dfrac{x + 3}{x − 2} ≥ 0\)
    2. \(\dfrac{x − 2}{x − 1} ≤ 0\)
    3. \(\dfrac{8}{x + 2}\) ≤\(\dfrac{1}{x + 2}\)
    4. \(\dfrac{2x − 3}{x + 1} ≥ 0\)

     

    Exercise Solutions \(\PageIndex{1}\)

    \(\dfrac{x + 3}{x − 2} ≥ 0\)

    Solution

    Set x + 3 = 0 and solve for x.

    x + 3 = 0
       -3      -3
    x = -3

    Set x - 2 = 0 and solve for x.
    x - 2= 0
       2     2
    X + 0 = 2
    x = 2

    Because we have the line under the inequality, ≥, we will include -3 and 2 in the solution.

    The number line is divided into three regions.  Left of -3,  between -3 and 2, to the right of 2.  Pick a point in each region.

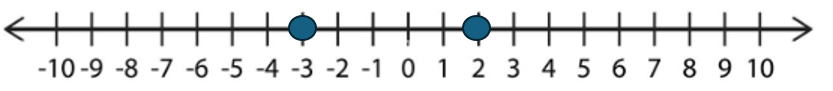
    clipboard_e9e39b933d7b7e2dae0efd716df4b9c3b.png

    x = -4 

    \(\dfrac{-4+3}{-4-2}\) = \(\dfrac{-1}{-6}\) = \(\dfrac{1}{6}\) ≥ 0.  The area to the left of -3 is a solution.  The interval notation is clipboard_e130c599c386bfd80e6b7b7f6c7a5e681.png

    x = 0

    \(\dfrac{0+3}{0-2}\) = \(\dfrac{3}{-2}\) < 0.  The area between -3 and 2 is not a solution.

    x = 3

    \(\dfrac{3+3}{3-2}\) = \(\dfrac{6}{1}\) = 6 ≥ 0.  The area to the right of 2 is a solution.  The interval notation is 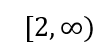clipboard_ec67ac169a44f707bc8ab171b31f8e0ac.png

    The solution is 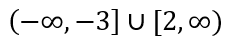clipboard_e1294baf98bc85507c2d2399d518b68f9.png in Interval Notation.

    clipboard_eae9f895c3b6f2716d8b3aff3da63d0c1.png

    \(\begin{array} &&\text{For } x < −1, \text{ choose } x = −2. \;\;\dfrac{−2 − 1}{−2 + 1} = \dfrac{−3}{−1} = 3 ≥ 0 \\ &\text{Replacing \(-2\) for \(x\) results in the answer \(3\), which is greater than or equal to \(0\). This region \(x < −1\) is included in the solution set.} \\[0.25in] &\text{For } −1 < x < 1, \text{ choose } x = 0.\;\; \dfrac{0 − 1}{0 + 1} = \dfrac{−1}{1} = −1 < 0 \\ &\text{Replacing \(0\) for \(x\) results in the answer \(-1\), which is less than \(0\), not fulfilling the given inequality in the problem.} \\ &\text{This region \(−1 < x < 1\) is excluded from the solution set.} \\[0.25in] &\text{For } x > 1, \text{ choose } x = 2.\;\; \dfrac{2 − 1}{2 + 1} = \dfrac{1}{3} ≥ 0 \\ &\text{Replacing \(2\) for \(x\) results in the answer \(\dfrac{1}{3}\), which is greater than or equal to \(0\). This region \(x > 1\) is included in the solution set.} \\[0.25in] &(−∞, −1) ∪ (1, ∞) \\ &\text{Final answer written in interval notation (see section on Interval Notation for more details).} \end{array}\)

    1. \(\begin{array} &&\dfrac{2x − 3}{x + 1} ≤ 0 &\text{Example problem} \\ &\dfrac{2x − 3}{x + 1} ≤ 0 &\text{The quotient must be less than or equal to \(0\).} \\ &2x − 3 = 0,\; x = 1.5 &\text{Find the zeroes of the numerator} \\ &x + 1 = 0,\; x = −1 &\text{Find the zeroes of the denominator} \end{array}\)
    clipboard_eb1a3fd2706ba7b03d6acdeb3ad51ec07.png
    The zeroes divide the number line into \(3\) regions, \(x < −1\), \(−1 < x < 1.5\), \(x > 1.5\)

    \(\begin{array} &&\text{For } -1< x, \text{ choose } x = -2. \;\;\dfrac{2(-2) - 3}{-2 + 1} = \dfrac{−7}{-1} = 7 ≥ 0 \\ &\text{Replacing \(-2\) for \(x\) results in the answer \(7\), which is greater than or equal to \(0\). This region \(-1 < x\) is excluded in the solution set.} \end{array}\)

    \(\begin{array} &&\text{For } -1< x < 1.5, \text{ choose } x = 0. \;\;\dfrac{2(0) - 3}{0 + 1} = \dfrac{−3}{1} = -3 ≤ 0 \\ &\text{Replacing \(0\) for \(x\) results in the answer \(-3\), which is less than or equal to \(0\). This region \(-1 < x < 1.5\) is included in the solution set.} \end{array}\)

    \(\begin{array} &&\text{For } x > 1.5, \text{ choose } x =2. \;\;\dfrac{2(2) - 3}{2 + 1} = \dfrac{1}{3} ≥ 0 \\ &\text{Replacing \(2\) for \(x\) results in the answer \(\dfrac{1}{3}\), which is greater than or equal to \(0\). This region \(x > 1.5 \) is excluded in the solution set.} \end{array}\)

    \(\begin{array} &&\text{(-1, 1.5)} \end{array}\)

    \(\begin{array} &&\text{Final answer written in interval notation (see section on Interval Notation for more details).} \end{array}\)

     

    1. \(\begin{array} &&\dfrac{x + 2}{x − 2} ≥ 0 &\text{Example problem} \\ &\dfrac{x + 2}{x − 2} ≥ 0 &\text{The quotient must be greater than or equal to \(0\).} \\ &x + 2 = 0, \;\;x = −2 &\text{Find the zeroes of the numerator} \\ &x − 2 = 0,\;\; x = 2 &\text{Find the zeroes of the denominator} \end{array}\)
    clipboard_e3374fd2eab55feb8c3dfe2d5ebd8d557.png
    The zeroes divide the number line into \(3\) regions, \(x < −2\), \(−2 < x < 2\), \(x > 2\)

    \(\begin{array} &&\text{For } x < −2, \text{ choose } x = −3. \dfrac{−3 + 2}{−3 − 2} = \dfrac{−1}{−5} = \dfrac{1}{5} ≥ 0 \\ &\text{Replacing \(-3\) for \(x\) results in the answer \(\dfrac{1}{5}\), which is greater than or equal to \(0\). This region \(x < −2\) is included in the solution set.} \\[0.25in] &\text{For } −2 < x < 2, \text{ choose } x = 0. \;\; \dfrac{0 + 2}{0 − 2} = \dfrac{2}{−2} = −1 < 0 \\ &\text{Replacing \(0\) for \(x\) results in the answer \(-1\), which is less than \(0\), not fulfilling the given inequality in the problem.} \\ &\text{This region \(−2 < x < 2\) is not included in the solution set.} \\[0.25in] &\text{For } x > 2, \text{ choose } x = 3. \;\; \dfrac{3 + 2}{3 − 2} = \dfrac{5}{1} = 5 ≥ 0 \\ &\text{Replacing \(3\) for \(x\) results in the answer \(5\), which is greater than or equal to \(0\). This region \(x > 2\) is included in the solution set.} \\[0.25in] &(−∞, −2) ∪ (2, ∞) \\ &\text{Final answer written in interval notation (see section on Interval Notation for more details).} \end{array}\)

    Exercise \(\PageIndex{1}\)

    \(\dfrac{8}{x + 2}\) ≤\(\dfrac{1}{x + 2}\)

    Answer

    Add texts here. Do not delete this text first.

    Subtract \(\dfrac{1}{x-2}\) from both sides

    \(\dfrac{8}{x + 2}\) - \(\dfrac{1}{x + 2}\) ≤ 0

    \(\dfrac{7}{x + 2}\) ≤ 0

    There is only a variable in the denominator so we set x + 2 = 0 and solve for x.

    x + 2 = 0
       -2      -2
    x + 0 = -2
    x = -2

    Since x = -2 results in 0 in the denominator x = -2 is not a part of the solution.  -2 breaks the number line into two parts: to the left of -2 and to the right of -2.

    clipboard_e713edd548a2418ac65084abba1c4d763.png

    Pick a number both regions.

    x = -3 and substitute it in the rational expression.

    \(\dfrac{8}{-3 + 2}\)  = \(\dfrac{8}{-1}\)  = -8

    \(\dfrac{1}{-3 + 2}\) = \(\dfrac{1}{-1}\) = -1

    -8 < -1  The region to the left of -2 is part of the solution.  Interval Notation clipboard_e944a5abf582438f25a7cc2fb74263c1e.png.

    x = 0

    \(\dfrac{8}{0 + 2}\)  = \(\dfrac{8}{2}\)  = 4

    \(\dfrac{1}{0 + 2}\) = \(\dfrac{1}{2}\) 

    4 >  \(\dfrac{1}{2}\)    Therefore, this region is not a part of the solution.

    The solution is clipboard_e944a5abf582438f25a7cc2fb74263c1e.png.

    clipboard_e63c6b450e4b0fb9c366c9fe26c0df0dc.png

     

    This page titled 2.4: Rational Inequalities is shared under a CC BY-NC-SA 4.0 license and was authored, remixed, and/or curated by OpenStax.

    This page titled 2.4: Rational Inequalities is shared under a CC BY-NC-SA 4.0 license and was authored, remixed, and/or curated by Victoria Dominguez, Cristian Martinez, & Sanaa Saykali (ASCCC Open Educational Resources Initiative) .