Tree Diagrams and Counting
- Page ID
- 222
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)We have seen that probability is defined by
\[ P(E) = \dfrac {\text{Number in E}}{\text{Number in the Sample Space}} \nonumber \]
Although this formula appears simple, counting the number in each can prove to be a challenge. Visual aids will help us immensely.
A native flowering plant has several varieties. The color of the flower can be red, yellow, or white. The stems can be long or short and the leaves can be thorny, smooth, or velvety. Show all varieties.
Solution
We use a tree diagram, which is a diagram that branches out and ends in leaves that correspond to the final variety. The picture below shows this.
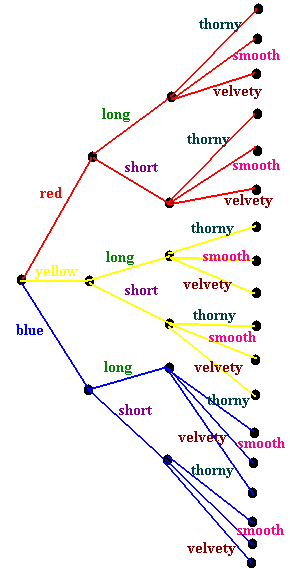
To read this tree diagram, we begin from start. then move along the branches collecting words until we get to the end. For example,
- Always taking the upper path leads to the selection of a red long thorny plant.
- Always taking the lower path leads to a blue short velvety plant. We can count the total number of leaves (path endings) and get that there are 18 possible varieties.
- Counting the leaves that came from long stems tell us that there are 9 possible long stemmed varieties.
A committee of three republican senators and four democratic senators is selected to investigate corporate securities fraud. Out of this committee two members are to be selected at random for a subcommittee on the energy sector.
- What is the probability that both members will be republican?
- What is the probability that both members will be democrat?
- What is the probability of one of each?
Solution
We write a tree diagram
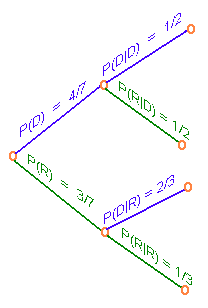
In this tree diagram, D represents democrat and R represents republican. The probabilities are given in the diagram.
To answer part A, we need to find
\[ P(\text{ first is } R \text{ and second is } R) \nonumber \]
This corresponds to the bottom leaf. As we travel to the bottom leaf, we pick up the two numbers
\[ P(R \text{ and } R) = \dfrac{3}{7}\dfrac{1}{3} = \dfrac{1}{7}\nonumber \]
To answer part B, we need to find
\[ P(\text{ first is } D \text{ and second is } D) \nonumber \]
This corresponds to the top leaf. We have
\[ P(D \text{ and } D) = \dfrac{4}{7}\dfrac{1}{2} = \dfrac{2}{7} \nonumber \]
To answer the part C we add the two middle leaves
\[ \begin{align*} P((D \text{ and }R) \text{ or } (R \text{ and }D)) &= \dfrac{4}{7}\dfrac{1}{2} + \dfrac{3}{7}\dfrac{2}{3} \\[5pt] &= \dfrac{2}{7} + \dfrac{2}{7} \\[5pt] &= \dfrac{4}{7} \end{align*} \]
Permutations
Suppose that 40 women try out for the newest play that has an all women cast of seven. You are the director. How many choices do you have?
Solution
The way to work this problem out is to consider the main role first. You have 40 choices for the main role. For the lead supporting actor there are 39 left to select from. For the next role there are 38 to select from. Now following this pattern and consider that there are seven in the cast gives a total number of choices as
\[ 40 \cdot 39 \cdot 38 \cdot 37 .\cdot 36 \cdot 35 \cdot 34 \nonumber \]
We could multiply these all out, however there is an easier way. We can write
\[ 40 \cdot 39 \cdot 38 \cdot 37 \cdot 36 \cdot 35 \cdot 34 \left( \dfrac{33 \cdot 32 \cdot 31 \cdot \, ... \cdot 2 . 1}{ 33 \cdot 32 \cdot 31 \cdot\, ... \cdot 2 \cdot 1} \right) = \dfrac{40!}{(40-7)!} \nonumber \]
This expression has a special notation. We write
\[ P_{40,7} = \dfrac{n!}{(n-r)!} = 93,963,542,400 \nonumber \]
We can see that there are plenty of choices. In general we write
\[ P_{n,r} = \dfrac{n!}{(n-r)!} \nonumber \]
This is called a permutation.
Combinations
How many 5 card poker hands are there?
Solution
We can solve this in a similar way as the prior question. We are selecting 5 cards out of 52 total. Unfortunately this is not quite a permutation since, for example, the hand
2H 3H 4H 5H 6H
is the same as the hand
3H 5H 2H 6H 4H
where "H" means hearts. That is the order at which the cards are dealt does not matter. The number of ways of ordering 5 cards is 5! (five choices for the first card, four left for the second, three left for the third, two for the fourth, and one for the fifth). We divide by this number to get our solution
\[ = \dfrac{52!}{(52-5)! \; 5!} \nonumber \]
We write this with the notation
\[ C_{52,5} = \dfrac{52!}{(52-5)! \; 5!} = 2,598,960 \nonumber \]
In general, we have
\[ C_{n,k} = \dfrac{n!}{(n-k)! \; k!} \nonumber \]
and call this a combination.
The following was taken from the California state lottery web site:
"SuperLottoPlus is your chance to win millions of dollars! The jackpot ranges from $7 million to $50 million or more. The jackpot rolls over and grows whenever there is no winner. All you have to do is pick five numbers from 1 to 47 and one MEGA number from 1 to 27 and match them to the numbers drawn by the Lottery every Wednesday and Saturday."
What is the probability of winning the lottery?
Solution
There is only one element in the event space. Your numbers. For the sample space, first they pick 5 numbers from 47. There are
\[ C_{47,5} =1,533,939 \nonumber \]
ways of doing this. Next they select a number from 1 to 27. There are 27 ways of doing this. We multiply to get
\[ 1,533,939\; \times \; 27 = 41,416,353 \nonumber \]
So your chances are worse than one in forty-million.