1.4: Partial Orders
- Page ID
- 10119
Partial orders are a special class of relations that play an important role in probability theory.
Basic Theory
A partial order on a set \(S\) is a relation \(\preceq\) on \(S\) that is reflexive, anti-symmetric, and transitive. The pair \( (S, \preceq) \) is called a partially ordered set. So for all \( x, \ y, \ z \in S \):
- \( x \preceq x \), the reflexive property
- If \( x \preceq y \) and \( y \preceq x \) then \( x = y \), the antisymmetric property
- If \( x \preceq y \) and \( y \preceq z \) then \( x \preceq z \), the transitive property
As the name and notation suggest, a partial order is a type of ordering of the elements of \(S\). Partial orders occur naturally in many areas of mathematics, including probability. A partial order on a set naturally gives rise to several other relations on the set.
Suppose that \( \preceq \) is a partial order on a set \( S \). The relations \(\succeq\), \(\prec\), \(\succ\), \(\perp\), and \(\parallel\) are defined as follows:
- \(x \succeq y\) if and only if \(y \preceq x\).
- \(x \prec y\) if and only if \(x \preceq y\) and \(x \ne y\).
- \(x \succ y\) if and only if \(y \prec x\).
- \(x \perp y\) if and only if \(x \preceq y\) or \(y \preceq x\).
- \(x \parallel y\) if and only if neither \( x \preceq y \) nor \( y \preceq x \).
Note that \( \succeq \) is the inverse of \( \preceq \), and \(\succ \) is the inverse of \( \prec \). Note also that \( x \preceq y \) if and only if either \( x \prec y \) or \( x = y \), so the relation \( \prec \) completely determines the relation \( \preceq \). The relation \(\prec\) is sometimes called a strict or strong partial order to distingush it from the ordinary (weak) partial order \(\preceq\). Finally, note that \( x \perp y \) means that \( x \) and \( y \) are related in the partial order, while \( x \parallel y \) means that \( x \) and \( y \) are unrelated in the partial order. Thus, the relations \( \perp \) and \( \parallel \) are complements of each other, as sets of ordered pairs. A total or linear order is a partial order in which there are no unrelated elements.
A partial order \(\preceq\) on \(S\) is a total order or linear order if for every \(x, \ y \in S\), either \(x \preceq y\) or \(y \preceq x\).
Suppose that \(\preceq_1\) and \(\preceq_2\) are partial orders on a set \(S\). Then \(\preceq_1\) is an sub-order of \(\preceq_2\), or equivalently \(\preceq_2\) is an extension of \(\preceq_1\) if and only if \(x \preceq_1 y\) implies \( x \preceq_2 y\) for \(x, \ y \in S\).
Thus if \( \preceq_1 \) is a suborder of \( \preceq_2 \), then as sets of ordered pairs, \(\preceq_1\) is a subset of \(\preceq_2\). We need one more relation that arises naturally from a partial order.
Suppose that \(\preceq\) is a partial order on a set \(S\). For \(x, \ y \in S\), \(y\) is said to cover \(x\) if \(x \prec y\) but no element \(z \in S\) satisfies \(x \prec z \prec y\).
If \(S\) is finite, the covering relation completely determines the partial order, by virtue of the transitive property.
Suppose that \(\preceq\) is a partial order on a finite set \(S\). The covering graph or Hasse graph of \((S, \preceq)\) is the directed graph with vertex set \(S\) and directed edge set \(E\), where \((x, y) \in E\) if and only if \(y\) covers \(x\).
Thus, \(x \prec y\) if and only if there is a directed path in the graph from \(x\) to \(y\). Hasse graphs are named for the German mathematician Helmut Hasse. The graphs are often drawn with the edges directed upward. In this way, the directions can be inferred without having to actually draw arrows.
Basic Examples
Of course, the ordinary order \(\le\) is a total order on the set of real numbers \(\R\). The subset partial order is one of the most important in probability theory:
Suppose that \(S\) is a set. The subset relation \(\subseteq\) is a partial order on \(\mathscr{P}(S)\), the power set of \(S\).
Proof
We proved this result in the section on sets. To review, recall that for \( A, \ B \in \mathscr{P}(S) \), \( A \subseteq B \) means that \( x \in A \) implies \( x \in B \). Also \( A = B \) means that \( x \in A \) if and only if \( x \in B \). Thus
- \( A \subseteq A \)
- \( A \subseteq B \) and \( B \subseteq A \) if and only if \( A = B \)
- \( A \subseteq B \) and \( B \subseteq C \) imply \( A \subseteq C \)
Here is a partial order that arises naturally from arithmetic.
Let \(\mid\) denote the division relation on the set of positive integers \(\N_+\). That is, \(m \mid n\) if and only if there exists \(k \in \N_+\) such that \(n = k m\). Then
- \(\mid\) is a partial order on \(\N_+\).
- \(\mid\) is a sub-order of the ordinary order \(\le\).
Proof
- Clearly \( n \mid n \) for \( n \in \N_+ \), since \( n = 1 \cdot n \), so \( \mid \) is reflexive. Suppose \( m \mid n \) and \( n \mid m \), where \( m, \ n \in \N_+ \). Then there exist \( j, \ k \in \N_+ \) such that \( n = k m \) and \( m = j n \). Substituting gives \( n = j k n \), and hence \( j = k = 1 \). Thus \( m = n \) so \( \mid \) is antisymmetric. Finally, suppose \( m \mid n \) and \( n \mid p \), where \( m, \ n, \ p \in \N_+ \). Then there exists \( j, \ k \in \N_+ \) such that \( n = j m \) and \( p = k n \). Substituting gives \( p = j k m \), so \( m \mid p \). Thus \( \mid \) is transitive.
- If \( m, \ n \in \N_+ \) and \( m \mid n \), then there exists \( k \in \N_+ \) such that \( n = k m \). Since \( k \ge 1 \), \( m \le n \).
The set of functions from a set into a partial ordered set can itself be partially ordered in a natural way.
Suppose that \( S \) is a set and that \( (T, \preceq_T) \) is a partially ordered set, and let \( \mathscr{S} \) denote the set of functions \( f: S \to T \). The relation \( \preceq \) on \( \mathscr{S} \) defined by \( f \preceq g \) if and only \( f(x) \preceq_T g(x) \) for all \( x \in S \) is a partial order on \( \mathscr{S} \).
Proof
Suppose that \( f, \, g, \, h \in \mathscr{S} \).
- \( f(x) \preceq_T f(x) \) for all \( x \in S \), so \( f \preceq f \).
- If \( f \preceq g \) and \( g \preceq f \) then \( f(x) \preceq_T g(x) \) and \( g(x) \preceq_T f(x) \) for all \( x \in S \). Hence \( f(x) = g(x) \) for all \( x \in S \) so \( f = g \).
- If \( f \preceq g \) and \( g \preceq h \) then \( f(x) \preceq_T g(x) \) and \( g(x) \preceq_T h(x) \) for all \( x \in S \). Hence \( f(x) \preceq_T h(x) \) for all \( x \in S \) so \( f \preceq h \).
Note that we don't need a partial order on the domain \( S \).
Basic Properties
The proofs of the following basic properties are straightforward. Be sure to try them yourself before reading the ones in the text.
The inverse of a partial order is also a partial order.
Proof
Clearly the reflexive, antisymmetric and transitive properties hold for \( \succeq \).
If \(\preceq\) is a partial order on \(S\) and \(A\) is a subset of \(S\), then the restriction of \(\preceq\) to \(A\) is a partial order on \(A\).
Proof
The reflexive, antisymmetric, and transitive properties given above hold for all \( x, \ y, \ z \in S \) and hence hold for all \( x, \ y, \ z \in A \).
The following theorem characterizes relations that correspond to strict order.
Let \(S\) be a set. A relation \(\preceq\) is a partial order on \(S\) if and only if \(\prec\) is transitive and irreflexive.
Proof
Suppose that \( \preceq \) is a partial order on \( S \). Recall that \( \prec \) is defined by \( x \prec y \) if and only if \( x \preceq y \) and \( x \ne y \). If \( x \prec y \) and \( y \prec z \) then \( x \preceq y \) and \( y \preceq z \), and so \( x \preceq z \). On the other hand, if \( x = z \) then \( x \preceq y \) and \( y \preceq x \) so \( x = y \), a contradiction. Hence \( x \ne z \) and so \(x \prec z\). Therefore \( \prec \) is transitive. If \( x \prec y \) then \( x \ne y \) by definition, so \( \prec \) is irreflexive.
Conversely, suppose that \( \prec \) is a transitive and irreflexive relation on \( S \). Recall that \( \preceq \) is defined by \( x \preceq y \) if and only if \( x \prec y \) or \( x = y \). By definition then, \( \preceq \) is reflexive: \( x \preceq x \) for every \( x \in S \). Next, suppose that \( x \preceq y \) and \( y \preceq x \). If \( x \prec y \) and \( y \prec x \) then \( x \prec x \) by the transitive property of \( \prec \). But this is a contradiction by the irreflexive property, so we must have \( x = y \). Thus \( \preceq \) is antisymmetric. Suppose \( x \preceq y \) and \( y \preceq z \). There are four cases:
- If \( x \prec y \) and \( y \prec z \) then \( x \prec z \) by the transitive property of \( \prec \).
- If \( x = y \) and \( y \prec z \) then \( x \prec z \) by substitution.
- If \( x \prec y \) and \( y = z \) then \( x \prec z \) by substitution.
- If \( x = y \) and \( y = z \) then \( x = z \) by the transitive property of \( = \).
In all cases we have \( x \preceq z \) so \( \preceq \) is transitive. Hence \( \preceq \) is a partial order on \( S \).
Monotone Sets and Functions
Partial orders form a natural setting for increasing and decreasing sets and functions. Here are the definitions:
Suppose that \(\preceq\) is a partial order on a set \(S\) and that \(A \subseteq S\). In the following definitions, \(x, \, y\) are arbitrary elements of \(S\).
- \(A\) is increasing if \(x \in A\) and \(x \preceq y\) imply \(y \in A\).
- \(A\) is decreasing if \(y \in A\) and \(x \preceq y\) imply \(x \in A\).
Suppose that \(S\) is a set with partial order \(\preceq_S\), \(T\) is a set with partial order \(\preceq_T\), and that \(f: S \to T\). In the following definitions, \(x, \, y\) are arbitrary elements of \(S\).
- \(f\) is increasing if and only if \(x \preceq_S y\) implies \(f(x) \preceq_T f(y)\).
- \(f\) is decreasing if and only if \(x \preceq_S y\) implies \(f(x) \succeq_T f(y)\).
- \(f\) is strictly increasing if and only if \(x \prec_S y\) implies \(f(x) \prec_T f(y)\).
- \(f\) is strictly decreasing if and only if \(x \prec_S y\) implies \(f(x) \succ_T f(y)\).
Recall the definition of the indicator function \(\bs{1}_A\) associated with a subset \( A \) of a universal set \( S \): For \( x \in S \), \( \bs{1}_A(x) = 1 \) if \( x \in A \) and \( \bs{1}_A(x) = 0 \) if \( x \notin A \).
Suppose that \(\preceq\) is a partial order on a set \(S\) and that \(A \subseteq S\). Then
- \(A\) is increasing if and only if \(\boldsymbol{1}_A\) is increasing.
- \(A\) is decreasing if and only if \(\boldsymbol{1}_A\) is decreasing.
Proof
- \( A \) is increasing if and only if \( x \in A \) and \( x \preceq y \) implies \( y \in A \) if and only if \( \bs{1}_A(x) = 1 \) and \( x \le y \) implies \( \bs{1}_A(y) = 1 \) if and only if \( \bs{1}_A \) is increasing.
- \( A \) is decreasing if and only if \( y \in A \) and \( x \preceq y \) implies \( x \in A \) if and only if \( \bs{1}_A(y) = 1 \) and \( x \le y \) implies \( \bs{1}_A(x) = 1 \) if and only if \( \bs{1}_A \) is decreasing.
Isomorphism
Two partially ordered sets \( (S, \preceq_S) \) and \( (T, \preceq_T) \) are said to be isomorphic if there exists a one-to-one function \( f \) from \( S \) onto \( T \) such that \( x \preceq_S y \) if and only if \( f(x) \preceq_T f(y) \), for all \( x, \ y \in S \). The function \( f \) is an isomorphism.
Generally, a mathematical space often consists of a set and various structures defined in terms of the set, such as relations, operators, or a collection of subsets. Loosely speaking, two mathematical spaces of the same type are isomorphic if there exists a one-to-one function from one of the sets onto the other that preserves the structures, and again, the function is called an isomorphism. The basic idea is that isomorphic spaces are mathematically identical, except for superficial matters of appearance. The word isomorphism is from the Greek and means equal shape.
Suppose that the partially ordered sets \( (S, \preceq_S) \) and \( (T, \preceq_T) \) are isomorphic, and that \( f: S \to T \) is an isomorphism. Then \( f \) and \( f^{-1} \) are strictly increasing.
Proof
We need to show that for \( x, \ y \in S \), \( x \prec_S y \) if and only if \( f(x) \prec_T f(y) \). If \( x \prec_S y \) then by definition, \( f(x) \preceq_T f(y) \). But if \( f(x) = f(y) \) then \( x = y \) since \( f \) is one-to-one. This is a contradiction, so \( f(x) \prec_T f(y) \). Similarly, if \( f(x) \prec_T f(y) \) then by definition, \( x \preceq_S y \). But if \( x = y \) then \( f(x) = f(y) \), a contradiction. Hence \( x \prec_S y \).
In a sense, the subset partial order is universal—every partially ordered set is isomorphic to \((\mathscr{S}, \subseteq)\) for some collection of sets \(\mathscr{S}\).
Suppose that \(\preceq\) is a partial order on a set \(S\). Then there exists \( \mathscr{S} \subseteq \mathscr{P}(S) \) such that \( (S, \preceq) \) is isomorphic to \( (\mathscr{S}, \subseteq)\).
Proof
For each \(x \in S\), let \(A_x = \{u \in S: u \preceq x\}\), and then let \(\mathscr{S} = \{A_x: x \in S\}\), so that \(\mathscr{S} \subseteq \mathscr{P}(S)\). We will show that the function \(x \mapsto A_x\) from \(S\) onto \(\mathscr{S}\) is one-to-one, and satisfies \[ x \preceq y \iff A_x \subseteq A_y \] First, suppose that \( x, \ y \in S \) and \( A_x = A_y \). Then \( x \in A_x \) so \( x \in A_y \) and hence \( x \preceq y \). Similarly, \( y \in A_y \) so \( y \in A_x \) and hence \( y \preceq x \). Thus \( x = y \), so the mapping is one-to-one. Next, suppose that \( x \preceq y \). If \( u \in A_x \) then \( u \preceq x \) so \( u \preceq y \) by the transitive property, and hence \( u \in A_y \). Thus \( A_x \subseteq A_y \). Conversely, suppose \( A_x \subseteq A_y \). As before, \( x \in A_x \), so \( x \in A_y \) and hence \( x \preceq y \).
Extremal Elements
Various types of extremal elements play important roles in partially ordered sets. Here are the definitions:
Suppose that \(\preceq\) is a partial order on a set \(S\) and that \(A \subseteq S\).
- An element \(a \in A\) is the minimum element of \(A\) if and only if \(a \preceq x\) for every \(x \in A\).
- An element \(a \in A\) is a minimal element of \(A\) if and only if no \(x \in A\) satisfies \(x \prec a\).
- An element \(b \in A\) is the maximum element of \(A\) if and only if \(b \succeq x\) for every \(x \in A\).
- An element \(b \in A\) is a maximal element of \(A\) if and only if no \(x \in A\) satisfies \(x \succ b\).
In general, a set can have several maximal and minimal elements (or none). On the other hand,
The minimum and maximum elements of \(A\), if they exist, are unique. They are denoted \(\min(A)\) and \(\max(A)\), respectively.
Proof
Suppose that \( a, \ b \) are minimum elements of \( A \). Since \( a, \ b \in A \) we have \( a \preceq b \) and \( b \preceq a \), so \( a = b \) by the antisymmetric property. The proof for the maximum element is analogous.
Minimal, maximal, minimum, and maximum elements of a set must belong to that set. The following definitions relate to upper and lower bounds of a set, which do not have to belong to the set.
Suppose again that \( \preceq \) is a partial order on a set \( S \) and that \( A \subseteq S \). Then
- An element \(u \in S\) is a lower bound for \(A\) if and only if \(u \preceq x\) for every \(x \in A\).
- An element \(v \in S\) is an upper bound for \(A\) if and only if \(v \succeq x\) for every \(x \in A\).
- The greatest lower bound or infimum of \(A\), if it exists, is the maximum of the set of lower bounds of \(A\).
- The least upper bound or supremum of \(A\), if it exists, is the minimum of the set of upper bounds of \(A\).
By (20), the greatest lower bound of \(A\) is unique, if it exists. It is denoted \(\text{glb}(A)\) or \(\inf(A)\). Similarly, the least upper bound of \(A\) is unique, if it exists, and is denoted \(\text{lub}(A)\) or \(\sup(A)\). Note that every element of \(S\) is a lower bound and an upper bound for \(\emptyset\), since the conditions in the definition hold vacuously.
The symbols \( \wedge \) and \( \vee \) are also used for infimum and supremum, respectively, so \( \bigwedge A = \inf(A) \) and \( \bigvee A = \sup(A) \) if they exist.. In particular, for \( x, \ y \in S \), operator notation is more commonly used, so \( x \wedge y = \inf\{x, y\} \) and \( x \vee y = \sup\{x, y\} \). Partially ordered sets for which these elements always exist are important, and have a special name.
Suppose that \(\preceq\) is a partial order on a set \(S\). Then \((S, \preceq)\) is a lattice if \( x \wedge y \) and \( x \vee y \) exist for every \( x, \ y \in S \).
For the subset partial order, the inf and sup operators correspond to intersection and union, respectively:
Let \(S\) be a set and consider the subset partial order \(\subseteq\) on \(\mathscr{P}(S)\), the power set of \(S\). Let \(\mathscr{A}\) be a nonempty subset of \(\mathscr{P}(S)\), that is, a nonempty collection of subsets of \(S\). Then
- \(\inf(\mathscr{A}) = \bigcap \mathscr{A}\)
- \(\sup(\mathscr{A}) = \bigcup \mathscr{A}\)
Proof
- First, \( \bigcap \mathscr{A} \subseteq A \) for every \( A \in \mathscr{A} \) and hence \( \bigcap \mathscr{A} \) is a lower bound of \( \mathscr{A} \). If \( B \) is a lower bound of \( \mathscr{A} \) then \( B \subseteq A \) for every \( A \in \mathscr{A} \) and hence \( B \subseteq \bigcap \mathscr{A} \). Therefore \( \bigcap \mathscr{A} \) is the greatest lower bound.
- First, \(A \subseteq \bigcup \mathscr{A} \) for every \( A \in \mathscr{A} \) and hence \( \bigcup \mathscr{A} \) is an upper bound of \( \mathscr{A} \). If \( B \) is an upper bound of \( \mathscr{A} \) then \( A \subseteq B \) for every \( A \in \mathscr{A} \) and hence \( \bigcup \mathscr{A} \subseteq B \). Therefore \( \bigcup \mathscr{A} \) is the least upper bound.
In particular, \( A \wedge B = A \cap B \) and \( A \vee B = A \cup B \), so \( (\mathscr P(S), \subseteq) \) is a lattice.
Consider the division partial order \(\mid\) on the set of positive integers \(\N_+\) and let \(A\) be a nonempty subset of \(\N_+\).
- \(\inf(A)\) is the greatest common divisor of \(A\), usually denoted \(\gcd(A)\) in this context.
- If \(A\) is infinite then \(\sup(A)\) does not exist. If \(A\) is finite then \(\sup(A)\) is the least common multiple of \(A\), usually denoted \(\text{lcm}(A)\) in this context.
Suppose that \(S\) is a set and that \(f: S \to S\). An element \(z \in S\) is said to be a fixed point of \(f\) if \(f(z) = z\).
The following result explores a basic fixed point theorem for a partially ordered set. The theorem is important in the study of cardinality.
Suppose that \(\preceq\) is a partial order on a set \(S\) with the property that \(\sup(A)\) exists for every \(A \subseteq S\). If \(f: S \to S\) is increasing, then \(f\) has a fixed point.
Proof.
Let \(A = \{x \in S: x \preceq f(x)\}\) and let \(z = \sup(A)\). If \(x \in A\) then \(x \preceq z\) so \(x \preceq f(x) \preceq f(z)\). Hence \(f(z)\) is an upper bound of \(A\) so \(z \preceq f(z)\). But then \(f(z) \preceq f\left(f(z)\right)\) so \(f(z) \in A\). Hence \(f(z) \preceq z\). Therefore \(f(z) = z\).
Note that the hypotheses of the theorem require that \(\sup(\emptyset) = \min(S)\) exists. The set \(A = \{x \in S: x \preceq f(x)\}\) is nonempty since \(\min(S) \in A\).
If \( \preceq \) is a total order on a set \( S \) with the property that every nonempty subset of \( S \) has a minimum element, then \( S \) is said to be well ordered by \( \preceq \). One of the most important examples is \( \N_+ \), which is well ordered by the ordinary order \( \le \). On the other hand, the well ordering principle, which is equivalent to the axiom of choice, states that every nonempty set can be well ordered.
Orders on Product Spaces
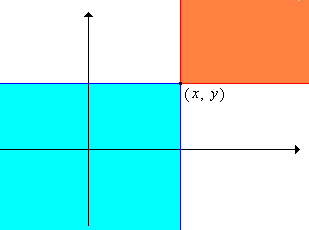
Suppose that \(S\) and \(T\) are sets with partial orders \(\preceq_S\) and \(\preceq_T\) respectively. Define the relation \(\preceq\) on \(S \times T\) by \((x, y) \preceq (z, w)\) if and only if \(x \preceq_S z\) and \(y \preceq_T w\).
- The relation \(\preceq\) is a partial order on \(S \times T\), called, appropriately enough, the product order.
- Suppose that \((S, \preceq_S) = (T, \preceq_T)\). If \(S\) has at least 2 elements, then \(\preceq\) is not a total order on \(S^2\).
Proof
Product order extends in a straightforward way to the Cartesian product of a finite or an infinite sequence of partially ordered spaces. For example, suppose that \( S_i \) is a set with partial order \( \preceq_i \) for each \( i \in \{1, 2, \ldots, n\} \), where \( n \in \N_+ \). The product order \( \preceq \) on the product set \( S_1 \times S_2 \times \cdots \times S_n \) is defined as follows: for \( \bs{x} = (x_1, x_2, \ldots, x_n) \) and \( \bs{y} = (y_1, y_2, \ldots, y_n) \) in the product set, \( \bs{x} \preceq \bs{y} \) if and only if \( x_i \preceq_i y_i \) for each \( i \in \{1, 2, \ldots, n\} \). We can generalize this further to arbitrary product sets. Suppose that \( S_i \) is a set for each \( i \) in a nonempty (both otherwise arbitrary) index set \( I \). Recall that \[ \prod_{i \in I} S_i = \left\{x: x \text{ is a function from } I \text{ into } \bigcup_{i \in I } S_i \text{ such that } x(i) \in S_i \text{ for each } i \in I \right\}\] To make the notation look more like a simple Cartesian product, we will write \( x_i \) instead of \( x(i) \) for the value of a function \( x \) in the product set at \( i \in I \).
Suppose that \( S_i \) is a set with partial order \( \preceq_i \) for each \( i \) in a nonempty index set \( I \). Define the relation \( \preceq \) on \( \prod_{i \in I} S_i \) by \( x \preceq y \) if and only if \( x_i \preceq_i y_i \) for each \( i \in I \). Then \( \preceq \) is a partial order on the product set, known again as the product order.
Proof
In spite of the abstraction, the proof is perfectly straightforward. Suppose that \( x, \, y, \, z \in \prod_{i \in I} S_i \).
- \( x_i \preceq_i x_i \) for every \( i \in I \), and hence \( x \preceq x \). Thus \( \preceq \) is reflexive.
- Suppose that \( x \preceq y \) and \( y \preceq x \). Then \( x_i \preceq_i y_i \) and \( y_i \preceq_i x_i \) for each \( i \in I \). Hence \( x_i = y_i \) for each \( i \in I \) and so \( x = y \). Thus \( \preceq \) is antisymmetric
- Suppose that \( x \preceq y \) and \( y \preceq z \). Then \( x_i \preceq_i y_i \) and \( y_i \preceq_i z_i \) for each \( i \in I \). Hence \( x_i \preceq_i z_i \) for each \( i \in I \), so \( x \preceq z \). Thus \( \preceq \) is transitive.
Note again that no assumptions are made on the index set \( I \), other than it be nonempty. In particular, no order is necessary on \( I \). The next result gives a very different type of order on a product space.
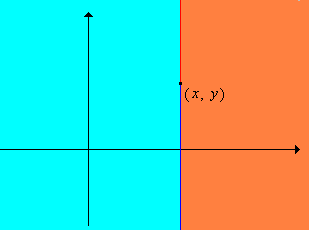
Suppose again that \(S\) and \(T\) are sets with partial orders \(\preceq_S\) and \(\preceq_T\) respectively. Define the relation \(\preceq\) on \(S \times T\) by \((x, y) \preceq (z, w)\) if and only if either \(x \prec_S z\), or \(x = z\) and \(y \preceq_T w\).
- The relation \(\preceq\) is a partial order on \(S \times T\), called the lexicographic order or dictionary order.
- If \(\preceq_S\) and \(\preceq_T\) are total orders on \(S\) and \(T\), respectively, then \(\preceq\) is a total order on \(S \times T\).
Proof
As with the product order, the lexicographic order can be generalized to a collection of partially ordered spaces. However, we need the index set to be totally ordered.
Suppose that \( S_i \) is a set with partial order \( \preceq_i \) for each \( i \) in a nonempty index set \( I \). Suppose also that \( \le \) is a total order on \( I \). Define the relation \( \preceq \) on the product set \( \prod_{i \in I} S_i \) as follows: \( x \prec y \) if and only if there exists \( j \in I \) such that \( x_i = y_i \) if \( i \lt j \) and \( x_j \prec_j y_j \). Then
- \( \preceq \) is a partial order on \( S \), known again as the lexicographic order.
- If \( \preceq_i \) is a total order for each \( i \in I \), and \( I \) is well ordered by \( \le \), then \( \preceq \) is a total order on \( S \).
Proof
- By the result on strong orders, we need to show that \( \prec \) is irreflexive and transitive. First, no \( x \in \prod_{i \in I} S_i\) satisfies \( x \prec x \) since \( x_i = x_i \) for all \( i \in I \). Hence \( \prec \) is irreflexive. Next, suppose that \( x, \ y, \ z \in \prod_{i \in I} S_i \) and that \( x \prec y \) and \( y \prec z \). Then there exists \( j \in I \) such that \( x_i = y_i \) if \( i \lt j \) and \( x_j \prec_j y_j \). Similarly, there exists \( k \in I \) such that \( y_i = z_i \) if \( i \lt k \) and \( y_k \prec_k z_k \). Again, since \( I \) is totally ordered, either \( j \lt k \) or \( k \lt j \) or \( j = k \). If \( j \lt k \), then \( x_i = y_i = z_i \) if \( i \lt j \) and \( x_j \prec_j y_j = z_j \). If \( k \lt j \), then \( x_i = y_i = z_i \) if \( i \lt k \) and \( x_k = y_k \prec_k z_k \). If \( j = k \), then \( x_i = y_i = z_i \) if \( i \lt j \) and \( x_j \prec_j y_j \prec_j z_j \). In all cases, \( x \prec z \) so \( \prec \) is transitive.
- Suppose now that \( \preceq_i \) is a total order on \( S_i \) for each \( i \in I \) and that \( I \) is well ordered by \( \le \). Let \( x, \ y \in \prod_{i \in I} S_i \) with \( x \ne y \). Let \( J = \{i \in I: x_i \ne y_i\} \). Then \( J \ne \emptyset\) by assumption, and hence has a minimum element \( j \). If \( i \lt j \) then \( i \notin J \) and hence \( x_i = y_i \). On the other hand, \( x_j \ne y_j \) since \( j \in J \) and therefore, since \( \preceq_j \) is totally ordered, we must have either \( x_j \prec_j y_j \) or \( y_j \prec_j x_j \). In the first case, \( x \prec y \) and in the second case \( y \prec x \). Hence \( \preceq \) is totally ordered.
The term lexicographic comes from the way that we order words alphabetically: We look at the first letter; if these are different, we know how to order the words. If the first letters are the same, we look at the second letter; if these are different, we know how to order the words. We continue in this way until we find letters that are different, and we can order the words. In fact, the lexicographic order is sometimes referred to as the first difference order. Note also that if \( S_i \) is a set and \( \preceq_i \) a total order on \( S_i \) for \( i \in I \), then by the well ordering principle, there exists a well ordering \( \le \) of \( I \), and hence there exists a lexicographic total order on the product space \( \prod_{i \in I} S_i \). As a mathematical structure, the lexicographic order is not as obscure as you might think.
\( (\R, \le) \) is isomorphic to the lexicographic product of \( (\Z, \le) \) with \( \left([0, 1), \le\right) \), where \( \le \) is the ordinary order for real numbers.
Proof
Every \( x \in \R \) can be uniquely expressed in the form \( x = n + t \) where \( n = \lfloor x \rfloor \in \Z \) is the integer part and \( t = x - n \in [0, 1) \) is the remainder. Thus \( x \mapsto (n, t) \) is a one-to-one function from \( \R \) onto \( \Z \times [0, 1) \). For example, \( 5.3 \) maps to \( (5, 0.3) \), while \( -6.7 \) maps to \( (-7, 0.3) \). Suppose that \( x = m + s, \ y = n + t \in \R \), where of course \( m, \, n \in \Z \) are the integer parts of \( x \) and \( y \), respectively, and \( s, \, t \in [0, 1) \) are the corresponding remainders. Then \( x \lt y \) if and only if \( m \lt n \) or \( m = n \) and \( s \lt t \). Again, to illustrate with real real numbers, we can tell that \( 5.3 \lt 7.8 \) just by comparing the integer parts: \( 5 \lt 7 \). We can ignore the remainders. On the other hand, to see that \( 6.4 \lt 6.7 \) we need to compare the remainders: \( 0.4 \lt 0.7 \) since the integer parts are the same.
Limits of Sequences of Real Numbers
Suppose that \((a_1, a_2, \ldots)\) is a sequence of real numbers.
The sequence \(\inf\{a_n, a_{n+1} \ldots\}\) is increasing in \(n \in \N_+\).
Since the sequence of infimums in the last result is increasing, the limit exists in \( \R \cup \{\infty\} \), and is called the limit inferior of the original sequence: \[ \liminf_{n \to \infty} a_n = \lim_{n \to \infty} \inf \{a_n, a_{n+1}, \ldots\} \]
The sequence \(\sup\{a_n, a_{n+1}, \ldots \}\) is decreasing in \(n \in \N_+\).
Since the the sequence of supremums in the last result is decreasing, the limit exists in \( \R \cup\{-\infty\} \), and is called the limit superior of the original sequence: \[ \limsup_{n \to \infty} a_n = \lim_{n \to \infty} \sup\{a_n, a_{n+1}, \ldots \} \] Note that \(\liminf_{n \to \infty} a_n \le \limsup_{n \to \infty} a_n\) and equality holds if and only if \(\lim_{n \to \infty} a_n\) exists (and is the common value).
Vector Spaces of Functions
Suppose that \( S \) is a nonempty set, and recall that the set \( \mathscr{V} \) of functions \( f: S \to \R \) is a vector space, under the usual pointwise definition of addition and scalar multiplication. As noted in (9), \( \mathscr{V} \) is also a partial ordered set, under the pointwise partial order: \( f \preceq g \) if and only if \( f(x) \le g(x) \) for all \( x \in S \). Consistent with the definitions (19), \( f \in \mathscr{V} \) is bounded if there exists \( C \in (0, \infty) \) such that \( \left|f(x)\right| \le C \) for all \( x \in S \). Now let \( \mathscr{U} \) denote the set of bounded functions \( f: S \to \R \), and for \( f \in \mathscr{U} \) define \[ \|f\| = \sup\{\left|f(x)\right|: x \in S\} \]
\( \mathscr{U} \) is a vector subspace of \( \mathscr{V} \) and \( \| \cdot \| \) is a norm on \( \mathscr{U} \).
Proof
To show that \( \mathscr{U} \) is a subspace, we just have to note that it is closed under addition and scalar multiplication. That is, if \( f, \, g: S \to \R \) are bounded, and if \( c \in \R \), then \( f + g \) and \( c f \) are bounded. Next we show that \( \| \cdot \| \) satisfies the axioms of a norm. Again, let \( f, \, g \in \mathscr{U} \) and \( c \in \R \)
- Clearly \( \|f\| \ge 0 \) and \( \|f\| = 0 \) if and only if \( f(x) = 0 \) for all \( x \in S \) if and only if \( f = \bs{0} \), the zero function on \( S \).
- \( \| c f\| = \sup\left\{\left|c f(x) \right|: x \in S\right\} = \left|c\right| \sup\left\{\left|f(x)\right|: x \in S\right\} = \left|c\right| \|f\| \)
- By the usual triangle inequality on \( \R \), \( \left|f(x) + g(x) \right| \le \left|f(x)\right| + \left|g(x)\right| \) for \( x \in S \). Hence \[ \sup\left\{\left|f(x) + g(x)\right|: x \in S\right\} \le \sup\left\{\left|f(x)\right| + \left|g(x)\right|: x \in S\right\} \le \sup\left\{\left|f(x)\right|: x \in S\right\} + \sup\left\{\left|g(x)\right|: x \in S\right\} \] That is, \( \|f + g\| \le \|f\| + \|g\| \).
Recall that part (a) is the positive property, part (b) is the scaling property, and part (c) is the triangle inequality.
Appropriately enough, \( \| \cdot \| \) is called the supremum norm on \( \mathscr{U} \). Vector spaces of bounded, real-valued functions, with the supremum norm are especially important in probability and random processes. We will return to this discussion again in the advanced sections on metric spaces and measure theory.
Computational Exercises
Let \(S = \{2, 3, 4, 6, 12\}\).
- Sketch the Hasse graph corresponding to the ordinary order \(\le\) on \(S\).
- Sketch the Hasse graph corresponding to the division partial order \(\mid\) on \(S\).
Answer
-
The Hasse graph of \( (S, \le) \) 
-
The Hasse graph of \( (S, |) \) 
Consider the ordinary order \(\le\) on the set of real numbers \(\R\), and let \(A = [a, b)\) where \(a \lt b\). Find each of the following that exist:
- The set of minimal elements of \(A\)
- The set of maximal elements of \(A\)
- \(\min(A)\)
- \(\max(A)\)
- The set of lower bounds of \(A\)
- The set of upper bounds of \(A\)
- \(\inf(A)\)
- \(\sup(A)\)
Answer
- \(\{a\}\)
- \(\emptyset\)
- \(a\)
- Does not exist
- \((-\infty, a]\)
- \([b, \infty)\)
- \(a\)
- \(b\)
Again consider the division partial order \(\mid\) on the set of positive integers \(\N_+\) and let \(A = \{2, 3, 4, 6, 12\}\). Find each of the following that exist:
- The set of minimal elements of \(A\)
- The set of maximal elements of \(A\)
- \(\min(A)\)
- \(\max(A)\)
- The set of lower bounds of \(A\)
- The set of upper bounds of \(A\)
- \(\inf(A)\)
- \(\sup(A)\).
Answer
- \(\{2, 3\}\)
- \(\{12\}\)
- Does not exist
- \(12\)
- \(\{1\}\)
- \(\{12, 24, 36, \ldots\}\)
- \(1\)
- \(12\)
Let \( S = \{a, b, c\} \).
- Give \( \mathscr{P}(S) \) in list form.
- Describe the Hasse graph of \( (\mathscr{P}(S), \subseteq) \)
Answer
- \( \mathscr{P}(S) = \{\emptyset, \{a\}, \{b\}, \{c\}, \{a, b\}, \{a, c\}, \{b, c\}, S\} \)
- For \( A \in \mathscr{P}(S) \) and \( x \in S \setminus A \), there is a directed edge from \( A \) to \( A \cup \{x\} \)
Note that the Hasse graph of \( \supseteq \) looks the same as the graph of \( \subseteq \), except for the labels on the vertices. This symmetry is because of the complement relationship.
Let \( S = \{a, b, c, d\} \).
- Give \( \mathscr{P}(S) \) in list form.
- Describe the Hasse graph of \( (\mathscr{P}(S), \subseteq) \)
Answer
- \( \mathscr{P}(S) = \{\emptyset, \{a\}, \{b\}, \{c\}, \{d\}, \{a, b\}, \{a, c\}, \{a, d\}, \{b, c\}, \{b, d\}, \{c, d\}, \{a, b, c\}, \{a, b, d\}, \{a, c, d\}, \{b, c, d\}, S\} \)
- For \( A \in \mathscr{P}(S) \) and \( x \in S \setminus A \), there is a directed edge from \( A \) to \( A \cup \{x\} \)
Note again that the Hasse graph of \( \supseteq \) looks the same as the graph of \( \subseteq \), except for the labels on the vertices. This symmetry is because the complement relationship.
Suppose that \( A \) and \( B \) are subsets of a universal set \( S \). Let \( \mathscr{A} \) denote the collection of the 16 subsets of \( S \) that can be constructed from \( A \) and \( B \) using the set operations. Show that \( (\mathscr{A}, \subseteq) \) is isomorphic to the partially ordered set in the previous exercise. Use the Venn diagram app to help.
Proof
Let \( a = A \cap B \), \( b = A \cap B^c \), \( c = A^c \cap B \), \( d = A^c \cap B^c \). Our basic assumption is that \( A \) and \( B \) are in general position
, so that \( a, \, b, \, c, \, d \) are distinct and nonempty. Note also that \( \{a, b, c, d\} \) partitions \( S \). Now, map each subset \( \mathscr{S} \) of \( \{a, b, c, d\} \) to \( \bigcup \mathscr{S} \). This function is an isomorphism from \( \mathscr{S} \) to \( \mathscr{A} \). That is, for \( \mathscr{S} \) and \( \mathscr{T} \) subsets of \( \{a, b, c, d\} \), \( \mathscr{S} \subseteq \mathscr{T} \) if and only if \( \bigcup \mathscr{S} \subseteq \bigcup \mathscr{T} \).


