1.1: Sets
- Page ID
- 10116
Set theory is the foundation of probability and statistics, as it is for almost every branch of mathematics.
Sets and subsets
In this text, sets and their elements are primitive, self-evident concepts, an approach that is sometimes referred to as naive set theory.
A set is simply a collection of objects; the objects are referred to as elements of the set. The statement that \(x\) is an element of set \(S\) is written \(x \in S\), and the negation that \( x \) is not an element of \( S \) is written as \( x \notin S \). By definition, a set is completely determined by its elements; thus sets \(A\) and \(B\) are equal if they have the same elements: \[ A = B \text{ if and only if } x \in A \iff x \in B \]
Our next definition is the subset relation, another very basic concept.
If \(A\) and \(B\) are sets then \(A\) is a subset of \(B\) if every element of \(A\) is also an element of \(B\): \[ A \subseteq B \text{ if and only if } x \in A \implies x \in B \]
Concepts in set theory are often illustrated with small, schematic sketches known as Venn diagrams, named for John Venn. The Venn diagram in the picture below illustrates the subset relation.
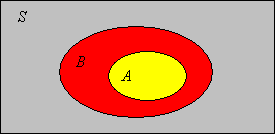
As noted earlier, membership is a primitive, undefined concept in naive set theory. However, the following construction, known as Russell's paradox, after the mathematician and philosopher Bertrand Russell, shows that we cannot be too cavalier in the construction of sets.
Let \(R\) be the set of all sets \( A \) such that \(A \notin A\). Then \(R \in R\) if and only if \(R \notin R\).
Proof
The contradiction follows from the definition of \( R \): If \( R \in R \), then by definition, \( R \notin R \). If \( R \notin R \), then by definition, \( R \in R \). The net result, of course, is that \( R \) is not a well-defined set.
Usually, the sets under discussion in a particular context are all subsets of a well-defined, specified set \(S\), often called a universal set. The use of a universal set prevents the type of problem that arises in Russell's paradox. That is, if \(S\) is a given set and \(p(x)\) is a predicate on \(S\) (that is, a valid mathematical statement that is either true or false for each \(x \in S\)), then \(\{x \in S: p(x)\}\) is a valid subset of \(S\). Defining a set in this way is known as predicate form. The other basic way to define a set is simply be listing its elements; this method is known as list form.
In contrast to a universal set, the empty set, denoted \(\emptyset\), is the set with no elements.
\(\emptyset \subseteq A\) for every set \(A\).
Proof
\( \emptyset \subseteq A \) means that \( x \in \emptyset \implies x \in A \). Since the premise is false, the implication is true.
One step up from the empty set is a set with just one element. Such a set is called a singleton set. The subset relation is a partial order on the collection of subsets of \(S\).
Suppose that \(A\), \(B\) and \(C\) are subsets of a set \(S\). Then
- \(A \subseteq A\) (the reflexive property).
- If \(A \subseteq B\) and \(B \subseteq A\) then \(A = B \) (the anti-symmetric property).
- If \(A \subseteq B\) and \(B \subseteq C\) then \(A \subseteq C\) (the transitive property).
Here are a couple of variations on the subset relation.
Suppose that \(A\) and \(B\) are sets.
- If \( A \subseteq B \) and \( A \ne B \), then \( A \) is a strict subset of \( B \) and we sometimes write \( A \subset B \).
- If \( \emptyset \subset A \subset B \), then \( A \) is called a proper subset of \( B \).
The collection of all subsets of a given set frequently plays an important role, particularly when the given set is the universal set.
If \(S\) is a set, then the set of all subsets of \(S\) is known as the power set of \(S\) and is denoted \(\mathscr{P}(S)\).
Special Sets
The following special sets are used throughout this text. Defining them will also give us practice using list and predicate form.
Special Sets
- \( \R \) denotes the set of real numbers and is the universal set for the other subsets in this list.
- \(\N = \{0, 1, 2, \ldots\}\) is the set of natural numbers
- \(\N_+ = \{1, 2, 3, \ldots\}\) is the set of positive integers
- \(\Z = \{\ldots, -2, -1, 0, 1, 2, \ldots\}\) is the set of integers
- \(\Q = \{m / n: m \in \Z \text{ and } n \in \N_+ \}\) is the set of rational numbers
- \( \A = \{x \in \R: p(x) = 0 \text{ for some polynomial } p \text{ with integer coefficients}\} \) is the set of algebraic numbers.
Note that \( \N_+ \subset \N \subset \Z \subset \Q \subset \A \subset \R \). We will also occasionally need the set of complex numbers \(\C = \{x + i y: x, \, y \in \R\}\) where \( i \) is the imaginary unit. The following special rational numbers turn out to be useful for various constructions.
For \( n \in \N \), a rational number of the form \( j / 2^n \) where \( j \in \Z \) is odd is a dyadic rational (or binary rational) of rank \( n \).
- For \( n \in \N \), the set of dyadic rationals of rank \( n \) or less is \( \D_n = \{j / 2^n: j \in \Z\} \).
- The set of all dyadic rationals is \( \D = \{j / 2^n: j \in \Z \text{ and } n \in \N\} \).
Note that \( \D_0 = \Z \) and \( \D_n \subset \D_{n+1} \) for \( n \in \N \), and of course, \( \D \subset \Q \). We use the usual notation for intervals of real numbers, but again the definitions provide practice with predicate notation.
Suppose that \( a, \, b \in \R \) with \( a \lt b \).
- \( [a, b] = \{x \in \R: a \le x \le b\} \). This interval is closed.
- \( (a, b) = \{x \in \R: a \lt x \lt b\} \). This interval is open.
- \( [a, b) = \{x \in \R: a \le x \lt b\} \). This interval is closed-open.
- \( (a, b] = \{x \in \R: a \lt x \le b\} \). This interval is open-closed.
The terms open and closed are actually topological concepts.
You may recall that \( x \in \R \) is rational if and only if the decimal expansion of \( x \) either terminates or forms a repeating block. The binary rationals have simple binary expansions (that is, expansions in the base 2 number system).
A number \( x \in \R \) is a binary rational of rank \( n \in \N_+ \) if and only if the binary expansion of \( x \) is finite, with \( 1 \) in position \( n \) (after the separator).
Proof
It suffices to consider \( x \in (0, 1) \). The result is very simple so we just give the first few cases.
- The number with rank 1 is \( 1/2 \) with binary expansion 0.1
- The numbers with rank 2 are \( 1/4 \) with expansion 0.01 and \( 3/4 \) with expansion 0.11
- The numbers with rank 3 are \( 1/8 \) with expansion 0.001, \( 3/8 \) with expansion 0.011, \( 5/8 \) with expansion 0.101, and \( 7/8 \) with expansion 0.111.
Set Operations
We are now ready to review the basic operations of set theory. For the following definitions, suppose that \(A\) and \(B\) are subsets of a universal set, which we will denote by \(S\).
The union of \(A\) and \(B\) is the set obtained by combining the elements of \(A\) and \(B\). \[ A \cup B = \{x \in S: x \in A \text{ or } x \in B\} \]
The intersection of \(A\) and \(B\) is the set of elements common to both \(A\) and \(B\): \[ A \cap B = \{x \in S: x \in A \text{ and } x \in B\}\] If \(A \cap B = \emptyset\) then \(A\) and \(B\) are disjoint.
So \(A\) and \(B\) are disjoint if the two sets have no elements in common.
The set difference of \(B\) and \(A\) is the set of elements that are in \(B\) but not in \(A\): \[ B \setminus A = \{x \in S: x \in B \text{ and } x \notin A\} \]
Sometimes (particularly in older works and particularly when \( A \subseteq B \)), the notation \( B - A \) is used instead of \( B \setminus A \). When \( A \subseteq B \), \( B - A \) is known as proper set difference.
The complement of \(A\) is the set of elements that are not in \(A\): \[ A^c = \{ x \in S: x \notin A\} \]
Note that union, intersection, and difference are binary set operations, while complement is a unary set operation.
In the Venn diagram app, select each of the following and note the shaded area in the diagram.
- \(A\)
- \(B\)
- \(A^c\)
- \(B^c\)
- \(A \cup B\)
- \(A \cap B\)
Basic Rules
In the following theorems, \(A\), \(B\), and \(C\) are subsets of a universal set \(S\). The proofs are straightforward, and just use the definitions and basic logic. Try the proofs yourself before reading the ones in the text.
\(A \cap B \subseteq A \subseteq A \cup B\).
The identity laws:
- \(A \cup \emptyset = A\)
- \(A \cap S = A\)
So the empty set acts as an identity relative to the union operation, and the universal set acts as an identiy relative to the intersection operation.
The idempotent laws:
- \(A \cup A = A\)
- \(A \cap A = A\)
The complement laws:
- \(A \cup A^c = S\)
- \(A \cap A^c = \emptyset\)
The double complement law: \((A^c)^c = A\)
The commutative laws:
- \(A \cup B = B \cup A\)
- \(A \cap B = B \cap A\)
Proof
These results follows from the commutativity of the or and and logical operators.
The associative laws:
- \(A \cup (B \cup C) = (A \cup B) \cup C\)
- \(A \cap (B \cap C) = (A \cap B) \cap C\)
Proof
These results follow from the associativity of the or and and logical operators.
Thus, we can write \(A \cup B \cup C\) without ambiguity. Note that \( x \) is an element of this set if and only if \( x \) is an element of at least one of the three given sets. Similarly, we can write \(A \cap B \cap C\) without ambiguity. Note that \( x \) is an element of this set if and only if \( x \) is an element of all three of the given sets.
The distributive laws:
- \(A \cap (B \cup C) = (A \cap B) \cup (A \cap C)\)
- \(A \cup (B \cap C) = (A \cup B) \cap (A \cup C)\)
Proof
- \( x \in A \cap (B \cup C) \) if and only if \( x \in A \) and \( x \in B \cup C \) if and only if \( x \in A \) and either \( x \in B \) or \( x \in C \) if and only if \( x \in A \) and \( x \in B\), or, \( x \in A \) and \( x \in C \) if and only if \( x \in A \cap B \) or \( x \in A \cap C \) if and only if \( x \in (A \cap B) \cup (A \cap C \).
- The proof is exactly the same as (a), but with or and and interchanged.
So intersection distributes over union, and union distributes over intersection. It's interesting to compare the distributive properties of set theory with those of the real number system. If \(x, \, y, \, z \in \R\), then \(x (y + z) = (x y) + (x z)\), so multiplication distributes over addition, but it is not true that \(x + (y z) = (x + y)(x + z)\), so addition does not distribute over multiplication. The following results are particularly important in probability theory.
DeMorgan's laws (named after Agustus DeMorgan):
- \((A \cup B)^c = A^c \cap B^c\)
- \((A \cap B)^c = A^c \cup B^c\).
Proof
- \( x \in (A \cup B)^c \) if and only if \( x \notin A \cup B \) if and only if \(x \notin A \) and \( x \notin B \) if and only \( x \in A^c \) and \( x \in B^c \) if and only if \( x \in A^c \cap B^c \)
- \( x \in (A \cap B)^c \) if and only if \( x \notin A \cap B \) if and only if \(x \notin A \) or \( x \notin B \) if and only \( x \in A^c \) or \( x \in B^c \) if and only if \( x \in A^c \cup B^c \)
The following result explores the connections between the subset relation and the set operations.
The following statements are equivalent:
- \(A \subseteq B\)
- \(B^c \subseteq A^c\)
- \(A \cup B = B\)
- \(A \cap B = A\)
- \(A \setminus B = \emptyset\)
Proof
- Recall that \( A \subseteq B \) means that \( x \in A \implies x \in B\).
- \( B^c \subseteq A^c \) means that \( x \notin B \implies x \notin A \). This is the contrapositive of (a) and hence is equivalent to (a).
- If \( A \subseteq B \) then clearly \( A \cup B = B \). Conversely suppose \( A \cup B = B \). If \( x \in A \) then \( x \in A \cup B \) so \( x \in B \). Hence \( A \subseteq B \).
- If \( A \subseteq B \) then clearly \( A \cap B = A \). Conversely suppose \( A \cap B = A \). If \( x \in A \) then \( x \in A \cap B \) and so \( x \in B \). Hence \( A \subseteq B \).
- Suppose \( A \subseteq B \). If \( x \in A \) then \( x \in B \) and so by definition, \( x \notin A \setminus B \). If \( x \notin A \) then again by definition, \( x \notin A \setminus B \). Thus \( A \setminus B = \emptyset \). Conversely suppose that \( A \setminus B = \emptyset \). If \( x \in A \) then \( x \notin A \setminus B \) so \( x \in B \). Thus \( A \subseteq B \).
In addition to the special sets defined earlier, we also have the following:
More special sets
- \( \R \setminus \Q \) is the set of irrational numbers
- \( \R \setminus \A \) is the set of transcendental numbers
Since \( \Q \subset \A \subset \R\) it follows that \( \R \setminus \A \subset \R \setminus \Q \), that is, every transcendental number is also irrational.
Set difference can be expressed in terms of complement and intersection. All of the other set operations (complement, union, and intersection) can be expressed in terms of difference.
Results for set difference:
- \(B \setminus A = B \cap A^c\)
- \(A^c = S \setminus A\)
- \(A \cap B = A \setminus (A \setminus B)\)
- \(A \cup B = S \setminus \left\{(S \setminus A) \setminus \left[(S \setminus A) \setminus (S \setminus B)\right]\right\}\)
Proof
- This is clear from the definition: \( B \setminus A = B \cap A^c = \{x \in S: x \in B \text{ and } x \notin A\} \).
- This follows from (a) with \( B = S \).
- Using (a), DeMorgan's law, and the distributive law, the right side is \[ A \cap (A \cap B^c)^c = A \cap (A^c \cup B) = (A \cap A^c) \cup (A \cap B) = \emptyset \cup (A \cap B) = A \cap B \]
- Using (a), (b), DeMorgan's law, and the distributive law, the right side is \[ \left[A^c \cap (A^c \cap B)^c \right]^c = A \cup (A^c \cap B) = (A \cup A^c) \cap (A \cup B) = S \cap (A \cup B) = A \cup B \]
So in principle, we could do all of set theory using the one operation of set difference. But as (c) and (d) suggest, the results would be hideous.
\((A \cup B) \setminus (A \cap B) = (A \setminus B) \cup (B \setminus A)\).
Proof
A direct proof is simple, but for practice let's give a proof using set algebra, in particular, DeMorgan's law, and the distributive law: \begin{align} (A \cup B) \setminus (A \cap B) & = (A \cup B) \cap (A \cap B)^c = (A \cup B) \cap (A^c \cup B^c) \\ & = (A \cap A^c) \cup (B \cap A^c) \cup (A \cap B^c) \cup (B \cap B^c) \\ & = \emptyset \cup (B \setminus A) \cup (A \setminus B) \cup \emptyset = (A \setminus B) \cup (B \setminus A) \end{align}
The set in the previous result is called the symmetric difference of \(A\) and \(B\), and is sometimes denoted \(A \bigtriangleup B\). The elements of this set belong to one but not both of the given sets. Thus, the symmetric difference corresponds to exclusive or in the same way that union corresponds to inclusive or. That is, \( x \in A \cup B \) if and only if \( x \in A \) or \( x \in B \) (or both); \( x \in A \bigtriangleup B \) if and only if \( x \in A \) or \( x \in B \), but not both. On the other hand, the complement of the symmetric difference consists of the elements that belong to both or neither of the given sets:
\((A \bigtriangleup B)^c = (A \cap B) \cup (A^c \cap B^c) = (A^c \cup B) \cap (B^c \cup A) \)
Proof
Again, a direct proof is simple, but let's give an algebraic proof for practice: \begin{align} (A \bigtriangleup B)^c & = \left[(A \cup B) \cap (A \cap B)^c \right]^c \\ & = (A \cup B)^c \cup (A \cap B) = (A^c \cap B^c) \cup (A \cap B) \\ & = (A^c \cup A) \cap (A^c \cup B) \cap (B^c \cup A) \cap (B^c \cup B) \\ & = S \cap (A^c \cup B) \cap (B^c \cup A) \cap S = (A^c \cup B) \cap (B^c \cup A) \end{align}
There are 16 different (in general) sets that can be constructed from two given events \(A\) and \(B\).
Proof
\( S \) is the union of 4 pairwise disjoint sets: \( A \cap B \), \( A \cap B^c \), \( A^c \cap B \), and \( A^c \cap B^c \). If \( A \) and \( B \) are in general position
, these 4 sets are distinct. Every set that can be constructed from \( A \) and \( B \) is a union of some (perhaps none, perhaps all) of these 4 sets. There are \( 2^4 = 16 \) sub-collections of the 4 sets.
Open the Venn diagram app. This app lists the 16 sets that can be constructed from given sets \( A \) and \( B \) using the set operations.
- Select each of the four subsets in the proof of the last exercise: \( A \cap B \), \( A \cap B^c \), \( A^c \cap B \), and \( A^c \cap B^c \). Note that these are disjoint and their union is \( S \).
- Select each of the other 12 sets and show how each is a union of some of the sets in (a).
General Operations
The operations of union and intersection can easily be extended to a finite or even an infinite collection of sets.
Definitions
Suppose that \(\mathscr{A}\) is a nonempty collection of subsets of a universal set \(S\). In some cases, the subsets in \(\mathscr{A}\) may be naturally indexed by a nonempty index set \(I\), so that \(\mathscr{A} = \{A_i: i \in I\}\). (In a technical sense, any collection of subsets can be indexed.)
The union of the collection of sets \(\mathscr{A}\) is the set obtained by combining the elements of the sets in \(\mathscr{A}\): \[ \bigcup \mathscr{A} = \{x \in S: x \in A \text{ for some } A \in \mathscr{A}\} \]
If \(\mathscr{A} = \{A_i: i \in I\} \), so that the collection of sets is indexed, then we use the more natural notation: \[ \bigcup_{i \in I} A_i =\{x \in S: x \in A_i \text{ for some } i \in I\} \]
The intersection of the collection of sets \(\mathscr{A}\) is the set of elements common to all of the sets in \(\mathscr{A}\): \[ \bigcap \mathscr{A} = \{x \in S: x \in A \text{ for all } A \in \mathscr{A}\} \]
If \(\mathscr{A} = \{A_i : i \in I\}\), so that the collection of sets is indexed, then we use the more natural notation: \[ \bigcap_{i \in I} A_i = \{x \in S: x \in A_i \text{ for all } i \in I\} \] Often the index set is an integer interval
of \( \N \). In such cases, an even more natural notation is to use the upper and lower limits of the index set. For example, if the collection is \( \{A_i: i \in \N_+\} \) then we would write \( \bigcup_{i=1}^\infty A_i \) for the union and \( \bigcap_{i=1}^\infty A_i \) for the intersection. Similarly, if the collection is \( \{A_i: i \in \{1, 2, \ldots, n\}\} \) for some \( n \in \N_+ \), we would write \( \bigcup_{i=1}^n A_i \) for the union and \( \bigcap_{i=1}^n A_i \) for the intersection.
A collection of sets \(\mathscr{A}\) is pairwise disjoint if the intersection of any two sets in the collection is empty: \(A \cap B = \emptyset\) for every \(A, \; B \in \mathscr{A}\) with \(A \ne B\).
A collection of sets \(\mathscr{A}\) is said to partition a set \(B\) if the collection \(\mathscr{A}\) is pairwise disjoint and \(\bigcup \mathscr{A} = B\).
Partitions are intimately related to equivalence relations. As an example, for \( n \in \N \), the set \[ \mathscr{D}_n = \left\{\left[\frac{j}{2^n}, \frac{j + 1}{2^n}\right): j \in \Z\right\} \] is a partition of \( \R \) into intervals of equal length \(1 / 2^n\). Note that the endpoints are the dyadic rationals of rank \( n \) or less, and that \( \mathscr{D}_{n+1} \) can be obtained from \( \mathscr{D}_n \) by dividing each interval into two equal parts. This sequence of partitions is one of the reasons that the dyadic rationals are important.
Basic Rules
In the following problems, \(\mathscr{A} = \{A_i : i \in I\}\) is a collection of subsets of a universal set \(S\), indexed by a nonempty set \(I\), and \(B\) is a subset of \(S\).
The general distributive laws:
- \( \left(\bigcup_{i \in I} A_i \right) \cap B = \bigcup_{i \in I} (A_i \cap B) \)
- \( \left(\bigcap_{i \in I} A_i \right) \cup B = \bigcap_{i \in I} (A_i \cup B) \)
Restate the laws in the notation where the collection \(\mathscr{A}\) is not indexed.
Proof
- \( x \) is an element of the set on the left or the right of the equation if and only if \( x \in B \) and \( x \in A_i \) for some \( i \in I \).
- \( x \) is an element of the set on the left or the right of the equation if and only if \( x \in B \) or \( x \in A_i \) for every \( i \in I \).
\( \left( \bigcup \mathscr{A} \right) \cap B = \bigcup\{A \cap B: A \in \mathscr{A}\} \), \( \left( \bigcap \mathscr{A} \right) \cup B = \bigcap\{A \cup B: A \in \mathscr{A}\} \)
The general De Morgan's laws:
- \( \left(\bigcup_{i \in I} A_i \right)^c = \bigcap_{i \in I} A_i^c \)
- \( \left(\bigcap_{i \in I} A_i \right)^c = \bigcup_{i \in I} A_i^c \)
Restate the laws in the notation where the collection \(\mathscr{A}\) is not indexed.
Proof
- \( x \in \left(\bigcup_{i \in I} A_i \right)^c \) if and only if \( x \notin \bigcup_{i \in I} A_i \) if and only if \( x \notin A_i \) for every \( i \in I \) if and only if \( x \in A_i^c \) for every \( i \in I \) if and only if \( x \in \bigcap_{i \in I} A_i^c \).
- \( x \in \left(\bigcap_{i \in I} A_i \right)^c \) if and only if \( x \notin \bigcap_{i \in I} A_i \) if and only if \( x \notin A_i \) for some \( i \in I \) if and only if \( x \in A_i^c \) for some \( i \in I \) if and only if \( x \in \bigcup_{i \in I} A_i^c \).
\( \left( \bigcup \mathscr{A} \right)^c = \bigcap\{A^c: A \in \mathscr{A}\}\), \( \left( \bigcap \mathscr{A} \right)^c = \bigcup\{A^c: A \in \mathscr{A}\}\)
Suppose that the collection \(\mathscr{A}\) partitions \(S\). For any subset \(B\), the collection \(\{A \cap B: A \in \mathscr{A}\}\) partitions \(B\).
Proof
Suppose \( \mathscr{A} = \{A_i: i \in I\} \) where \( I \) is an index set. If \( i, \, j \in I \) with \( i \ne j \) then \( (A_i \cap B) \cap (A_j \cap B) = (A_i \cap A_j) \cap B = \emptyset \cap B = \emptyset \), so the collection \( \{A_i \cap B: i \in I\} \) is disjoint. Moreover, by the distributive law, \[ \bigcup_{i \in I} (A_i \cap B) = \left(\bigcup_{i \in I} A_i\right) \cap B = S \cap B = B \]
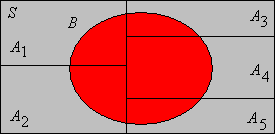
Figure \(\PageIndex{2}\): A partition of \( S \) induces a partition of \( B \)
Suppose that \( \{A_i: i \in \N_+\} \) is a collection of subsets of a universal set \( S \)
- \( \bigcap_{n=1}^\infty \bigcup_{k=n}^\infty A_k = \left\{x \in S: x \in A_k \text{ for infinitely many } k \in \N_+\right\} \)
- \( \bigcup_{n=1}^\infty \bigcap_{k=n}^\infty A_k = \left\{x \in S: x \in A_k \text{ for all but finitely many } k \in \N_+\right\} \)
Proof
- Note that \( x \in \bigcap_{n=1}^\infty \bigcup_{k=n}^\infty A_k \) if and only if for every \( n \in \N_+ \) there exists \( k \ge n \) such that \( x \in A_k \). In turn, this occurs if and only if \( x \in A_k \) for infinitely many \( k \in \N_+ \).
- Note that \( x \in \bigcup_{n=1}^\infty \bigcap_{k=n}^\infty A_k \) if and only if there exists \( n \in \N_+ \) such that \( x \in A_k \) for every \( k \ge n \). In turn, this occurs if and only if \( x \in A_k \) for all but finitely many \( k \in \N_+ \).
The sets in the previous result turn out to be important in the study of probability.
Product sets
Definitions
Product sets are sets of sequences. The defining property of a sequence, of course, is that order as well as membership is important.
Let us start with ordered pairs. In this case, the defining property is that \((a, b) = (c, d)\) if and only if \(a = c\) and \(b = d\). Interestingly, the structure of an ordered pair can be defined just using set theory. The construction in the result below is due to Kazimierz Kuratowski
Define \((a, b) = \{\{a\}, \{a, b\}\}\). This definition captures the defining property of an ordered pair.
Proof
Suppose that \( (a, b) = (c, d) \) so that \( \{\{a\}, \{a, b\}\} = \{\{c\}, \{c, d\}\} \). In the case that \( a = b \) note that \( (a, b) = \{\{a\}\} \). Thus we must have \( \{c\} = \{c, d\} = \{a\} \) and hence \( c = d = a \), and in particular, \( a = c \) and \( b = d \). In the case that \( a \ne b \), we must have \( \{c\} = \{a\} \) and hence \( c = a \). But we cannot have \( \{c, d\} = \{a\} \) because then \( (c, d) = \{\{a\}\} \) and hence \( \{a, b\} = \{a\} \), which would force \(a = b\), a contradiction. Thus we must have \( \{c, d\} = \{a, b\} \). Since \( c = a \) and \( a \ne b \) we must have \( d = b \). The converse is trivial: if \( a = c \) and \( b = d \) then \( \{a\} = \{c\} \) and \( \{a, b\} = \{c, d\} \) so \( (a, b) = (c, d) \).
Of course, it's important not to confuse the ordered pair \( (a, b) \) with the open interval \( (a, b) \), since the same notation is used for both. Usually it's clear form context which type of object is referred to. For ordered triples, the defining property is \( (a, b, c) = (d, e, f) \) if and only if \( a = d \), \( b = e \), and \( c = f \). Ordered triples can be defined in terms of ordered pairs, which via the last result, uses only set theory.
Define \( (a, b, c) = (a, (b, c)) \). This definition captures the defining property of an ordered triple.
Proof
Suppose \( (a, b, c) = (d, e, f) \). Then \( (a, (b, c)) = (d, (e, f)) \). Hence by the definition of an ordered pair, we must have \( a = d \) and \( (b, c) = (e, f) \). Using the definition again we have \( b = e \) and \( c = f \). Conversely, if \( a = d \), \( b = e \), and \( c = f \), then \((b, c) = (e, f)\) and hence \( (a, (b, c)) = (d, (e, f)) \). Thus \( (a, b, c) = (d, e, f) \).
All of this is just to show how complicated structures can be built from simpler ones, and ultimately from set theory. But enough of that! More generally, two ordered sequences of the same size (finite or infinite) are the same if and only if their corresponding coordinates agree. Thus for \( n \in \N_+ \), the definition for \( n \)-tuples is \( (x_1, x_2, \ldots, x_n) = (y_1, y_2, \ldots, y_n) \) if and only if \( x_i = y_i\) for all \( i \in \{1, 2, \ldots, n\} \). For infinite sequences, \((x_1, x_2, \ldots) = (y_1, y_2, \ldots) \) if and only if \( x_i = y_i \) for all \( i \in \N_+ \).
Suppose now that we have a sequence of \( n \) sets, \((S_1, S_2, \ldots, S_n)\), where \( n \in \N_+ \). The Cartesian product of the sets is defined as follows: \[ S_1 \times S_2 \times \cdots \times S_n = \left\{\left(x_1, x_2, \ldots, x_n\right): x_i \in S_i \text{ for } i \in \{1, 2, \ldots, n\}\right\} \]
Cartesian products are named for René Descartes. If \(S_i = S\) for each \(i\), then the Cartesian product set can be written compactly as \(S^n\), a Cartesian power. In particular, recall that \(\R\) denotes the set of real numbers so that \(\R^n\) is \(n\)-dimensional Euclidean space, named after Euclid, of course. The elements of \(\{0, 1\}^n\) are called bit strings of length \(n\). As the name suggests, we sometimes represent elements of this product set as strings rather than sequences (that is, we omit the parentheses and commas). Since the coordinates just take two values, there is no risk of confusion.
Suppose that we have an infinite sequence of sets \((S_1, S_2, \ldots)\). The Cartesian product of the sets is defined by \[ S_1 \times S_2 \times \cdots = \left\{\left(x_1, x_2, \ldots\right): x_i \in S_i \text{ for each } i \in \{1, 2, \ldots\}\right\} \]
When \( S_i = S \) for \( i \in \N_+ \), the Cartesian product set is sometimes written as a Cartesian power as \( S^\infty \) or as \( S^{\N_+} \). An explanation for the last notation, as well as a much more general construction for products of sets, is given in the next section on functions. Also, notation similar to that of general union and intersection is often used for Cartesian product, with \( \prod \) as the operator. So \[ \prod_{i=1}^n S_i = S_1 \times S_2 \times \cdots \times S_n, \quad \prod_{i=1}^\infty S_i = S_1 \times S_2 \times \cdots \]
Rules for Product Sets
We will now see how the set operations relate to the Cartesian product operation. Suppose that \(S\) and \(T\) are sets and that \(A \subseteq S\), \(B \subseteq S\) and \(C \subseteq T\), \(D \subseteq T\). The sets in the theorems below are subsets of \(S \times T\).
The most important rules that relate Cartesian product with union, intersection, and difference are the distributive rules:
Distributive rules for product sets
- \(A \times (C \cup D) = (A \times C) \cup (A \times D)\)
- \((A \cup B) \times C = (A \times C) \cup (B \times C)\)
- \(A \times (C \cap D) = (A \times C) \cap (A \times D)\)
- \((A \cap B) \times C = (A \times C) \cap (B \times C)\)
- \(A \times (C \setminus D) = (A \times C) \setminus (A \times D)\)
- \((A \setminus B) \times C = (A \times C) \setminus (B \times C)\)
Proof
- \( (x, y) \in A \times (C \cup D) \) if and only if \( x \in A \) and \( y \in C \cup D \) if and only if \( x \in A \) and either \( y \in C \) or \( y \in D \) if and only if \( x \in A \) and \( y \in C \), or, \( x \in A \) and \( y \in D \) if and only if \( (x, y) \in A \times C \) or \( (x, y) \in A \times D \) if and only if \( (x, y) \in (A \times C) \cup (A \times D) \).
- Similar to (a), but with the roles of the coordinates reversed.
- \( (x, y) \in A \times (C \cap D) \) if and only if \( x \in A \) and \( y \in C \cap D \) if and only if \( x \in A \) and \( y \in C \) and \( y \in D \) if and only if \( (x, y) \in A \times C \) and \( (x, y) \in A \times D \) if and only if \( (x, y) \in (A \times C) \cap (A \times D) \).
- Similar to (c) but with the roles of the coordinates reversed.
- \( (x, y) \in A \times (C \setminus D) \) if and only if \( x \in A \) and \( y \in C \setminus D \) if and only if \( x \in A \) and \( y \in C \) and \( y \notin D \) if and only if \( (x, y) \in A \times C \) and \( (x, y) \notin A \times D \) if and only if \( (x, y) \in (A \times C) \setminus (A \times D) \).
- Similar to (e) but with the roles of the coordinates reversed.
In general, the product of unions is larger than the corresponding union of products.
\((A \cup B) \times (C \cup D) = (A \times C) \cup (A \times D) \cup (B \times C) \cup (B \times D)\)
Proof
\( (x, y) \in (A \cup B) \times (C \cup D) \) if and only if \( x \in A \cup B \) and \( y \in C \cup D \) if and only if at least one of the following is true: \( x \in A \) and \( y \in C \), \( x \in A \) and \( y \in D \), \( x \in B \) and \( y \in C \), \( x \in B \) and \( y \in D \) if and only if \( (x, y) \in (A \times C) \cup (A \times D) \cup (B \times C) \cup (B \times D) \)
So in particular it follows that \((A \times C) \cup (B \times D) \subseteq (A \cup B) \times (C \cup D)\). On the other hand, the product of intersections is the same as the corresponding intersection of products.
\((A \times C) \cap (B \times D) = (A \cap B) \times (C \cap D)\)
Proof
\((x, y) \in (A \times C) \cap (B \times D)\) if and only if \( (x, y) \in A \times C \) and \( (x, y) \in B \times D \) if and only if \( x \in A \) and \( y \in C \) and \( x \in B \) and \( y \in D \) if and only if \( x \in A \cap B \) and \( y \in C \cap D \) if and only if \( (x, y) \in (A \cap B) \times (C \cap D) \).
In general, the product of differences is smaller than the corresponding difference of products.
\((A \setminus B) \times (C \setminus D) = [(A \times C) \setminus (A \times D)] \setminus [(B \times C) \setminus (B \times D)]\)
Proof
\( (x, y) \in (A \setminus B) \times (C \setminus D) \) if and only if \( x \in A \setminus B \) and \( y \in C \setminus D \) if and only if \( x \in A \) and \( x \notin B \) and \( y \in C \) and \( y \notin D \). On the other hand, \( (x, y) \in [(A \times C) \setminus (A \times D)] \setminus [(B \times C) \setminus (B \times D)] \) if and only if \( (x, y) \in (A \times C) \setminus (A \times D) \) and \( (x, y) \notin (B \times C) \setminus (B \times D) \). The first statement means that \( x \in A \) and \( y \in C \) and \( y \notin D \). The second statement is the negation of \( x \in B \) and \( y \in C \) and \( y \notin D \). The two statements both hold if and only if \( x \in A \) and \( x \notin B \) and \( y \in C \) and \( y \notin D \).
So in particular it follows that \((A \setminus B) \times (C \setminus D) \subseteq (A \times C) \setminus (B \times D)\),
Projections and Cross Sections
In this discussion, suppose again that \( S \) and \( T \) are nonempty sets, and that \( C \subseteq S \times T \).
Cross Sections
- The cross section of \( C \) in the first coordinate at \( x \in S \) is \(C_x = \{y \in T: (x, y) \in C\}\)
- The cross section of \( C \) at in the second coordinate at \( y \in T \) is \[ C^y = \{x \in S: (x, y) \in C\} \]
Note that \( C_x \subseteq T \) for \( x \in S \) and \( C^y \subseteq S \) for \( y \in T \).
Projections
- The projection of \(C\) onto \(T\) is \(C_T = \{y \in T: (x, y) \in C \text{ for some } x \in S\}\).
- The projection of \(C\) onto \(S\) is \(C^S = \{x \in S: (x, y) \in C \text{ for some } y \in T\}\).
The projections are the unions of the appropriate cross sections.
Unions
- \( C_T = \bigcup_{x \in S} C_x \)
- \( C^S = \bigcup_{y \in T} C^y \)
Cross sections are preserved under the set operations. We state the result for cross sections at \( x \in S \). By symmetry, of course, analgous results hold for cross sections at \( y \in T \).
Suppose that \( C, \, D \subseteq S \times T \). Then for \( x \in S \),
- \( (C \cup D)_x = C_x \cup D_x \)
- \( (C \cap D)_x = C_x \cap D_x \)
- \( (C \setminus D)_x = C_x \setminus D_x \)
Proof
- \( y \in (C \cup D)_x \) if and only if \( (x, y) \in C \cup D \) if and only if \( (x, y) \in C \) or \( (x, y) \in D \) if and only if \( y \in C_x \) or \( y \in D_x \).
- The proof is just like (a), with and replacing or.
- The proof is just like (a), with and not replacing or.
For projections, the results are a bit more complicated. We give the results for projections onto \( T \); naturally the results for projections onto \( S \) are analogous.
Suppose again that \( C, \, D \subseteq S \times T \). Then
- \( (C \cup D)_T = C_T \cup D_T \)
- \( (C \cap D)_T \subseteq C_T \cap D_T \)
- \( (C_T)^c \subseteq (C^c)_T \)
Proof
- Suppose that \( y \in (C \cup D)_T \). Then there exists \( x \in S \) such that \( (x, y) \in C \cup D \). Hence \( (x, y) \in C \) so \( y \in C_T \), or \( (x, y) \in D \) so \( y \in D_T \). In either case, \( y \in C_T \cup D_T \). Conversely, suppose that \( y \in C_T \cup D_T \). Then \( y \in C_T \) or \( y \in D_T \). If \( y \in C_T \) then there exists \( x \in S \) such that \( (x, y) \in C \). But then \( (x, y) \in C \cup D \) so \( y \in (C \cup D)_T \). Similarly if \( y \in D_T \) then \( y \in (C \cup D)_T \).
- Suppose that \( y \in (C \cap D)_T \). Then there exists \( x \in S \) such that \( (x, y) \in C \cap D \). Hence \( (x, y) \in C \) so \( y \in C_T \) and \( (x, y) \in D \) so \( y \in D_T \). Therefore \( y \in C_T \cap D_T \).
- Suppose that \( y \in (C_T)^c \). Then \( y \notin C_T \), so for every \( x \in S \), \( (x, y) \notin C \). Fix \( x_0 \in S \). Then \( (x_0, y) \notin C \) so \( (x_0, y) \in C^c \) and therefore \( y \in (C^c)_T \).
It's easy to see that equality does not hold in general in parts (b) and (c). In part (b) for example, suppose that \( A_1, \; A_2 \subseteq S \) are nonempty and disjoint and \( B \subseteq T \) is nonempty. Let \( C = A_1 \times B \) and \( D = A_2 \times B \). Then \( C \cap D = \emptyset \) so \( (C \cap D)_T = \emptyset \). But \( C_T = D_T = B \). In part (c) for example, suppose that \( A \) is a nonempty proper subset of \( S \) and \( B \) is a nonempty proper subset of \( T \). Let \( C = A \times B \). Then \( C_T = B \) so \( (C_T)^c = B^c \). On the other hand, \( C^c = (A^c \times B) \cup (A \times B^c) \cup (A^c \times B^c) \), so \( (C^c)_T = T \).
Cross sections and projections will be extended to very general product sets in the next section on Functions.
Computational Exercises
Subsets of \( \R \)
The universal set is \( [0, \infty) \). Let \( A = [0, 5] \) and \( B = (3, 7) \). Express each of the following in terms of intervals:
- \( A \cap B \)
- \( A \cup B \)
- \( A \setminus B \)
- \( B \setminus A \)
- \( A^c \)
Answer
- \( (3, 5] \)
- \( [0, 7) \)
- \( [0, 3] \)
- \( (5, 7) \)
- \( (5, \infty) \)
The universal set is \( \N \). Let \( A = \{n \in \N: n \text{ is even}\} \) and let \( B = \{n \in \N: n \le 9\} \). Give each of the following:
- \( A \cap B \) in list form
- \( A \cup B \) in predicate form
- \( A \setminus B \) in list form
- \( B \setminus A \) in list form
- \( A^c \) in predicate form
- \( B^c \) in list form
Answer
- \( \{0, 2, 4, 6, 8\} \)
- \( \{n \in \N: n \text{ is even or } n \le 9\} \)
- \( \{10, 12, 14, \ldots\} \)
- \( \{1, 3, 5, 7, 9\} \)
- \( \{n \in \N: n \text{ is odd}\} \)
- \( \{10, 11, 12, \ldots\} \)
Coins and Dice
Let \(S = \{1, 2, 3, 4\} \times \{1, 2, 3, 4, 5, 6\}\). This is the set of outcomes when a 4-sided die and a 6-sided die are tossed. Further let \(A = \{(x, y) \in S: x = 2\}\) and \(B = \{(x, y) \in S: x + y = 7\}\). Give each of the following sets in list form:
- \(A\)
- \(B\)
- \(A \cap B\)
- \(A \cup B\)
- \(A \setminus B\)
- \(B \setminus A\)
Answer
- \(\{(2, 1), (2, 2), (2, 3), (2, 4), (2, 5), (2, 6)\}\)
- \(\{(1, 6), (2, 5), (3, 4), (4, 3)\}\)
- \(\{(2, 5)\}\)
- \(\{(2, 1), (2, 2), (2, 3), (2, 4), (2, 5), (2, 6), (1, 6), (3, 4), (4, 3)\}\)
- \(\{(2, 1), (2, 2), (2, 3), (2, 4), (2, 6)\}\)
- \(\{(1, 6), (3, 4), (4, 3)\}\)
Let \(S = \{0, 1\}^3\). This is the set of outcomes when a coin is tossed 3 times (0 denotes tails and 1 denotes heads). Further let \(A = \{(x_1, x_2, x_3) \in S: x_2 = 1\}\) and \(B = \{(x_1, x_2, x_3) \in S: x_1 + x_2 + x_3 = 2\}\). Give each of the following sets in list form, using bit-string notation:
- \(S\)
- \(A\)
- \(B\)
- \(A^c\)
- \(B^c\)
- \(A \cap B\)
- \(A \cup B\)
- \(A \setminus B\)
- \(B \setminus A\)
Answer
- \(\{000, 100, 010, 001, 110, 101, 011, 111\}\)
- \(\{010, 110, 011, 111\}\)
- \(\{110, 011, 101\}\)
- \(\{000, 100, 001, 101\}\)
- \(\{000, 100, 010, 001, 111\}\)
- \(\{110, 011\}\)
- \(\{010, 110, 011, 111, 101\}\)
- \(\{010, 111\}\)
- \(\{101\}\)
Let \(S = \{0, 1\}^2\). This is the set of outcomes when a coin is tossed twice (0 denotes tails and 1 denotes heads). Give \(\mathscr{P}(S)\) in list form.
Answer
\(\{\emptyset, \{00\}, \{01\}, \{10\}, \{11\}, \{00, 01\}, \{00, 10\}, \{00, 11\}, \{01, 10\}, \{01, 11\}, \{10, 11\}, \{00, 01, 10\}, \{00, 01, 11\}, \{00, 10, 11\}, \{01, 10, 11\}, \{00, 01, 10, 11\}\}\)
Cards
A standard card deck can be modeled by the Cartesian product set \[ D = \{1, 2, 3, 4, 5, 6, 7, 8, 9, 10, j, q, k\} \times \{\clubsuit, \diamondsuit, \heartsuit, \spadesuit\} \] where the first coordinate encodes the denomination or kind (ace, 2–10, jack, queen, king) and where the second coordinate encodes the suit (clubs, diamonds, hearts, spades). Sometimes we represent a card as a string rather than an ordered pair (for example \(q \heartsuit\) for the queen of hearts). For the problems in this subsection, the card deck \(D\) is the universal set.
Let \(H\) denote the set of hearts and \(F\) the set of face cards. Find each of the following:
- \(H \cap F\)
- \(H \setminus F\)
- \(F \setminus H\)
- \(H \bigtriangleup F\)
Answer
- \(\{j \heartsuit, q \heartsuit, k \heartsuit\}\)
- \(\{1 \heartsuit, 2 \heartsuit, 3 \heartsuit, 4 \heartsuit, 5 \heartsuit, 6 \heartsuit, 7 \heartsuit, 8 \heartsuit, 9 \heartsuit, 10 \heartsuit\}\)
- \(\{j \spadesuit, q \spadesuit, k \spadesuit, j \diamondsuit, q \diamondsuit, k \diamondsuit, j \clubsuit, q \clubsuit, k \clubsuit\}\)
- \(\{1 \heartsuit, 2 \heartsuit, 3 \heartsuit, 4 \heartsuit, 5 \heartsuit, 6 \heartsuit, 7 \heartsuit, 8 \heartsuit, 9 \heartsuit, 10 \heartsuit, j \spadesuit, q \spadesuit, k \spadesuit, j \diamondsuit, q \diamondsuit, k \diamondsuit, j \clubsuit, q \clubsuit, k \clubsuit\}\)
A bridge hand is a subset of \( D \) with 13 cards. Often bridge hands are described by giving the cross sections by suit.
Suppose that \( N \) is a bridge hand, held by a player named North, defined by \[ N^\clubsuit = \{2, 5, q\}, \, N^\diamondsuit = \{1, 5, 8, q, k\}, \, N^\heartsuit = \{8, 10, j, q\}, \, N^\spadesuit = \{1\} \] Find each of the following:
- The nonempty cross sections of \( N \) by denomination.
- The projection of \( N \) onto the set of suits.
- The projection of \( N \) onto the set of denominations
Answer
- \( N_1 = \{\diamondsuit, \spadesuit\} \), \( N_2 = \{\clubsuit\} \), \( N_5 = \{\clubsuit, \diamondsuit\} \), \( N_8 = \{\diamondsuit, \heartsuit\} \), \( N_{10} = \{\heartsuit\} \), \( N_j = \{\heartsuit\} \), \( N_q = \{\clubsuit, \diamondsuit, \heartsuit\} \), \( N_k = \{\diamondsuit\} \)
- \( \{\clubsuit, \diamondsuit, \heartsuit, \spadesuit\} \)
- \( \{1, 2, 5, 8, 10, j, q, k\} \)
By contrast, it is usually more useful to describe a poker hand by giving the cross sections by denomination. In the usual version of draw poker, a hand is a subset of \( D \) with 5 cards.
Suppose that \( B \) is a poker hand, held by a player named Bill, with \[ B_1 = \{\clubsuit, \spadesuit\}, \, B_8 = \{\clubsuit, \spadesuit\}, \, B_q = \{\heartsuit\} \] Find each of the following:
- The nonempty cross sections of \( B \) by suit.
- The projection of \( B \) onto the set of suits.
- The projection of \( B \) onto the set of denominations
Answer
- \( B^\clubsuit = \{1, 8\} \), \( B^\heartsuit = \{q\} \), \( B^\spadesuit = \{1, 8\} \)
- \( \{\clubsuit, \heartsuit, \spadesuit\} \)
- \( \{1, 8, q\} \)
The poker hand in the last exercise is known as a dead man's hand. Legend has it that Wild Bill Hickock held this hand at the time of his murder in 1876.
General unions and intersections
For the problems in this subsection, the universal set is \(\R\).
Let \(A_n = [0, 1 - \frac{1}{n}]\) for \(n \in \N_+\). Find
- \(\bigcap_{n=1}^\infty A_n\)
- \(\bigcup_{n=1}^\infty A_n\)
- \(\bigcap_{n=1}^\infty A_n^c\)
- \(\bigcup_{n=1}^\infty A_n^c\)
Answer
- \(\{0\}\)
- \([0, 1)\)
- \((-\infty, 0) \cup [1, \infty)\)
- \(\R - \{0\}\)
Let \(A_n = (2 - \frac{1}{n}, 5 + \frac{1}{n})\) for \(n \in \N_+\). Find
- \(\bigcap_{n=1}^\infty A_n\)
- \(\bigcup_{n=1}^\infty A_n\)
- \(\bigcap_{n=1}^\infty A_n^c\)
- \(\bigcup_{n=1}^\infty A_n^c\)
Answer
- \([2, 5]\)
- \((1, 6)\)
- \((-\infty, 1] \cup [6, \infty)\)
- \((-\infty, 2) \cup (5, \infty)\)
Subsets of \( \R^2 \)
Let \( T \) be the closed triangular region in \( \R^2 \) with vertices \( (0, 0) \), \( (1, 0) \), and \( (1, 1) \). Find each of the following:
- The cross section \( T_x \) for \( x \in \R \)
- The cross section \( T^y \) for \( y \in \R \)
- The projection of \( T \) onto the horizontal axis
- The projection of \( T \) onto the vertical axis
Answer
- \( T_x = [0, x] \) for \( x \in [0, 1] \), \( T_x = \emptyset \) otherwise
- \( T^y = [y, 1] \) for \( y \in [0, 1] \), \( T^y = \emptyset \) otherwise
- \( [0, 1] \)
- \( [0, 1] \)


