1.2: Functions
- Page ID
- 10117
Functions play a central role in probability and statistics, as they do in every other branch of mathematics. For the most part, the proofs in this section are straightforward, so be sure to try them yourself before reading the ones in the text.
Definitions and Properties
Basic Definitions
We start with the formal, technical definition of a function. It's not very intuitive, but has the advantage that it only requires set theory.
A function \(f\) from a set \(S\) into a set \(T\) is a subset of the product set \(S \times T\) with the property that for each element \(x \in S\), there exists a unique element \(y \in T\) such that \((x, y) \in f\). If \(f\) is a function from \(S\) to \(T\) we write \(f: S \to T\). If \((x, y) \in f\) we write \(y = f(x)\).
Less formally, a function \(f\) from \(S\) into \(T\) is a rule
(or procedure
or algorithm
) that assigns to each \(x \in S\) a unique element \(f(x) \in T\). The definition of a function as a set of ordered pairs, is due to Kazimierz Kuratowski. The term map or mapping is also used in place of function, so we could say that \(f\) maps \(S\) into \(T\).
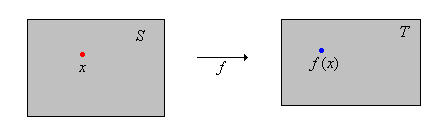
Figure \(\PageIndex{1}\): A function \( f\) from \( S \) into \( T \)
The sets \(S\) and \(T\) in the definition are clearly important.
Suppose that \(f: S \to T\).
- The set \(S\) is the domain of \(f\).
- The set \(T\) is the range space or co-domain of \(f\).
- The range of \(f\) is the set of function values. That is, \(\range\left(f\right) = \left\{y \in T: y = f(x) \text{ for some } x \in S\right\}\).
The domain and range are completely specified by a function. That's not true of the co-domain: if \(f\) is a function from \(S\) into \(T\), and \(U\) is another set with \(T \subseteq U\), then we can also think of \(f\) as a function from \(S\) into \(U\). The following definitions are natural and important.
Suppose again that \(f: S \to T\).
- \(f\) maps \(S\) onto \(T\) if \(\range\left(f\right) = T\). That is, for each \(y \in T\) there exists \(x \in S\) such that \(f(x) = y\).
- \(f\) is one-to-one if distinct elements in the domain are mapped to distinct elements in the range. That is, if \( u, \, v \in S \) and \( u \ne v \) then \( f(u) \ne f(v) \).
Clearly a function always maps its domain onto its range. Note also that \(f\) is one-to-one if \( f(u) = f(v) \) implies \( u = v \) for \(u, \, v \in S\).
Inverse functions
A funtion that is one-to-one and onto can be reversed
in a sense.
If \(f\) maps \(S\) one-to-one onto \(T\), the inverse of \(f\) is the function \(f^{-1}\) from \(T\) onto \(S\) given by \[ f^{-1}(y) = x \iff f(x) = y; \quad x \in S, \; y \in T \]
If you like to think of a function as a set of ordered pairs, then \(f^{-1} = \{(y, x) \in T \times S: (x, y) \in f\}\). The fact that \(f\) is one-to-one and onto ensures that \(f^{-1}\) is a valid function from \(T\) onto \(S\). Sets \(S\) and \(T\) are in one-to-one correspondence if there exists a one-to-one function from \(S\) onto \(T\). One-to-one correspondence plays an essential role in the study of cardinality.
Restrictions
The domain of a function can be restricted to create a new funtion.
Suppose that \(f: S \to T\) and that \(A \subseteq S\). The function \(f_A: A \to T\) defined by \(f_A(x) = f(x)\) for \( x \in A \) is the restriction of \(f\) to \(A\).
As a set of ordered pairs, note that \(f_A = \{(x, y) \in f: x \in A\}\).
Composition
Composition is perhaps the most important way to combine two functions to create another function.
Suppose that \(g: R \to S\) and \(f: S \to T\). The composition of \(f\) with \(g\) is the function \(f \circ g: R \to T\) defined by \[ \left(f \circ g\right)(x) = f\left(g(x)\right), \quad x \in R \]
Composition is associative:
Suppose that \(h: R \to S\), \(g: S \to T\), and \(f: T \to U\). Then \[ f \circ \left(g \circ h\right) = \left(f \circ g\right) \circ h \]
Proof
Note that both functions map \( R \) into \( U \). Using the definition of composition, the value of both functions at \( x \in R \) is \( f\left(g\left(h(x)\right)\right) \).
Thus we can write \(f \circ g \circ h\) without ambiguity. On the other hand, composition is not commutative. Indeed depending on the domains and co-domains, \( f \circ g \) might be defined when \( g \circ f \) is not. Even when both are defined, they may have different domains and co-domains, and so of course cannot be the same function. Even when both are defined and have the same domains and co-domains, the two compositions will not be the same in general. Examples of all of these cases are given in the computational exercises below.
Suppose that \(g: R \to S\) and \(f: S \to T\).
- If \(f\) and \(g\) are one-to-one then \(f \circ g\) is one-to-one.
- If \(f\) and \(g\) are onto then \(f \circ g\) is onto.
Proof
- Suppose that \( u, \, v \in R \) and \( (f \circ g)(u) = (f \circ g)(v) \). Then \( f\left(g(u)\right) = f\left(g(v)\right) \). Since \( f \) is one-to-one, \( g(u) = g(v) \). Since \( g \) is one-to-one, \( u = v \).
- Suppose that \( z \in T \). Since \( f \) is onto, there exist \( y \in S \) with \( f(y) = z \). Since \( g \) is onto, there exists \( x \in R \) with \( g(x) = y \). Then \( (f \circ g)(x) = f\left(g(x)\right) = f(y) = z \).
The identity function on a set \(S\) is the function \(I_S\) from \(S\) onto \(S\) defined by \(I_S(x) = x\) for \(x \in S\)
The identity function acts like an identity with respect to the operation of composition.
If \(f: S \to T\) then
- \(f \circ I_S = f\)
- \(I_T \circ f = f\)
Proof
- Note that \( f \circ I_S: S \to T \). For \( x \in S \), \( (f \circ I_S)(x) = f\left(I_S(x)\right) = f(x) \).
- Note that \( I_T \circ f: S \to T \). For \( x \in S \), \( (I_T \circ f)(x) = I_T\left(f(x)\right) = f(x) \).
The inverse of a function is really the inverse with respect to composition.
Suppose that \(f\) is a one-to-one function from \(S\) onto \(T\). Then
- \(f^{-1} \circ f = I_S\)
- \(f \circ f^{-1} = I_T\)
Proof
- Note that \( f^{-1} \circ f : S \to S \). For \( x \in S \), \( \left(f^{-1} \circ f\right)(x) = f^{-1}\left(f(x)\right) = x \).
- Note that \( f \circ f^{-1}: T \to T \). For \( y \in T \), \(\left(f \circ f^{-1}\right)(y) = f\left(f^{-1}(y)\right) = y \)
An element \(x \in S^n\) can be thought of as a function from \(\{1, 2, \ldots, n\}\) into \(S\). Similarly, an element \(x \in S^\infty\) can be thought of as a function from \(\N_+\) into \(S\). For such a sequence \(x\), of course, we usually write \(x_i\) instead of \(x(i)\). More generally, if \(S\) and \(T\) are sets, then the set of all functions from \(S\) into \(T\) is denoted by \(T^S\). In particular, as we noted in the last section, \( S^\infty \) is also (and more accurately) written as \( S^{\N_+} \).
Suppose that \(g\) is a one-to-one function from \(R\) onto \(S\) and that \(f\) is a one-to-one function from \(S\) onto \(T\). Then \(\left(f \circ g\right)^{-1} = g^{-1} \circ f^{-1}\).
Proof
Note that \( (f \circ g)^{-1}: T \to R \) and \( g^{-1} \circ f^{-1}: T \to R \). For \( y \in T \), let \(x = \left(f \circ g\right)^{-1}(y) \). Then \( \left(f \circ g\right)(x) = y \) so that \( f\left(g(x)\right) = y \) and hence \( g(x) = f^{-1}(y) \) and finally \( x = g^{-1}\left(f^{-1}(y)\right) \).
Inverse Images
Inverse images of a function play a fundamental role in probability, particularly in the context of random variables.
Suppose that \(f: S \to T\). If \(A \subseteq T\), the inverse image of \(A\) under \(f\) is the subset of \(S\) given by \[f^{-1}(A) = \{x \in S: f(x) \in A\}\]
So \(f^{-1}(A)\) is the subset of \(S\) consisting of those elements that map into \(A\).
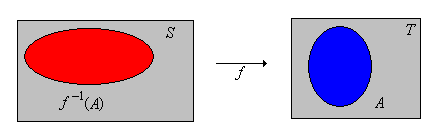
Figure \(\PageIndex{2}\): The inverse image of \( A \) under \( f \)
Technically, the inverse images define a new function from \(\mathscr{P}(T)\) into \(\mathscr{P}(S)\). We use the same notation as for the inverse function, which is defined when \(f\) is one-to-one and onto. These are very different functions, but usually no confusion results. The following important theorem shows that inverse images preserve all set operations.
Suppose that \(f: S \to T\), and that \(A, \, B \subseteq T\). Then
- \(f^{-1}(A \cup B) = f^{-1}(A) \cup f^{-1}(B)\)
- \(f^{-1}(A \cap B) = f^{-1}(A) \cap f^{-1}(B)\)
- \(f^{-1}(A \setminus B) = f^{-1}(A) \setminus f^{-1}(B)\)
- If \(A \subseteq B\) then \(f^{-1}(A) \subseteq f^{-1}(B)\)
- If \(A\) and \(B\) are disjoint, so are \(f^{-1}(A)\) and \(f^{-1}(B)\)
Proof
- \( x \in f^{-1}(A \cup B) \) if and only if \( f(x) \in A \cup B \) if and only if \( f(x) \in A \) or \( f(x) \in B \) if and only if \(x \in f^{-1}(A)\) or \( x \in f^{-1}(B) \) if and only if \( x \in f^{-1}(A) \cup f^{-1}(B) \)
- The proof is the same as (a), with intersection replacing union and with and replacing or throughout.
- The proof is the same as (a), with set difference replacing union and with and not replacing or throughout.
- Suppose \( A \subseteq B \). If \( x \in f^{-1}(A) \) then \( f(x) \in A \) and hence \( f(x) \in B \), so \( x \in f^{-1}(B) \).
- If \( A \) and \( B \) are disjoint, then from (b), \( f^{-1}(A) \cap f^{-1}(B) = f^{-1}(A \cap B) = f^{-1}(\emptyset) = \emptyset \).
The result in part (a) holds for arbitrary unions, and the result in part (b) holds for arbitrary intersections. No new ideas are involved; only the notation is more complicated.
Suppose that \( \{A_i: i \in I\} \) is a collection of subsets of \( T \), where \( I \) is a nonempty index set. Then
- \( f^{-1}\left(\bigcup_{i \in I} A_i\right) = \bigcup_{i \in I} f^{-1}(A_i) \)
- \( f^{-1}\left(\bigcap_{i \in I} A_i\right) = \bigcap_{i \in I} f^{-1}(A_i) \)
Proof
- \(x \in f^{-1}\left(\bigcup_{i \in I} A_i\right) \) if and only if \( f(x) \in \bigcup_{i \in I} A_i \) if and only if \( f(x) \in A_i \) for some \( i \in I \) if and only if \( x \in f^{-1}(A_i) \) for some \( i \in I \) if and only if \(x \in \bigcup_{i \in I} f^{-1}(A_i) \)
- The proof is the same as (a), with intersection replacing union and with for every replacing for some.
Forward Images
Forward images of a function are a naturally complement to inverse images.
Suppose again that \(f: S \to T\). If \(A \subseteq S\), the forward image of \(A\) under \(f\) is the subset of \(T\) given by \[ f(A) = \left\{f(x): x \in A\right\} \]
So \(f(A)\) is the range of \(f\) restricted to \(A\).
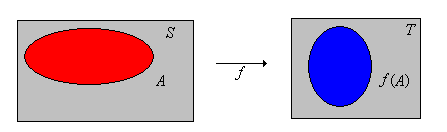
Figure \(\PageIndex{3}\): The forward image of \( A \) under \( f \)
Technically, the forward images define a new function from \(\mathscr{P}(S)\) into \(\mathscr{P}(T)\), but we use the same symbol \(f\) for this new function as for the underlying function from \(S\) into \(T\) that we started with. Again, the two functions are very different, but usually no confusion results.
It might seem that forward images are more natural than inverse images, but in fact, the inverse images are much more important than the forward ones (at least in probability and measure theory). Fortunately, the inverse images are nicer as well—unlike the inverse images, the forward images do not preserve all of the set operations.
Suppose that \(f: S \to T\), and that \(A, \, B \subseteq S\). Then
- \(f(A \cup B) = f(A) \cup f(B)\).
- \(f(A \cap B) \subseteq f(A) \cap f(B)\). Equality holds if \( f \) is one-to-one.
- \(f(A) \setminus f(B) \subseteq f(A \setminus B)\). Equality holds if \( f \) is one-to-one.
- If \(A \subseteq B\) then \(f(A) \subseteq f(B)\).
Proof
- Suppose \( y \in f(A \cup B) \). Then \( y = f(x) \) for some \( x \in A \cup B \). If \( x \in A \) then \( y \in f(A) \) and if \( x \in B \) then \( y \in f(B) \). In both cases \( y \in f(A) \cup f(B) \). Conversely suppose \( y \in f(A) \cup f(B) \). If \( y \in f(A) \) then \( y = f(x) \) for some \( x \in A \). But then \( x \in A \cup B \) so \( y \in f(A \cup B) \). Similarly, if \( y \in f(B) \) then \( y = f(x) \) for some \( x \in B \). But then \( x \in A \cup B \) so \( y \in f(A \cup B) \).
- If \( y \in f(A \cap B) \) then \( y = f(x) \) for some \( x \in A \cap B \). But then \( x \in A \) so \( y \in f(A) \) and \( x \in B \) so \( y \in f(B) \) and hence \( y \in f(A) \cap f(B) \). Conversely, suppose that \( y \in f(A) \cap f(B) \). Then \( y \in f(A) \) and \( y \in f(B) \), so there exists \( x \in A \) with \( f(x) = y \) and there exists \( u \in B \) with \( f(u) = y\). At this point, we can go no further. But if \( f \) is one-to-one, then \( u = x \) and hence \( x \in A \) and \( x \in B \). Thus \( x \in A \cap B \) so \( y \in f(A \cap B) \).
- Suppose \( y \in f(A) \setminus f(B) \). Then \( y \in f(A) \) and \( y \notin f(B) \). Hence \( y = f(x) \) for some \( x \in A \) and \( y \ne f(u) \) for every \( u \in B \). Thus, \( x \notin B \) so \( x \in A \setminus B \) and hence \( y \in f(A \setminus B) \). Conversely, suppose \( y \in f(A \setminus B) \). Then \( y = f(x) \) for some \( x \in A \setminus B \). Hence \( x \in A \) so \( y \in f(A) \). Again, the proof breaks down at this point. However, if \( f \) is one-to-one and \( f(u) = y \) for some \( u \in B \), then \( u = x \) so \( x \in B \), a contradiction. Hence \( f(u) \ne y \) for every \( u \in B \) so \( y \notin f(B) \). Thus \( y \in f(A \setminus B) \).
- Suppose \( A \subseteq B \). If \( y \in f(A) \) then \( y = f(x) \) for some \( x \in A \). But then \( x \in B \) so \( y \in f(B) \).
The result in part (a) hold for arbitrary unions, and the results in part (b) hold for arbitrary intersections. No new ideas are involved; only the notation is more complicated.
Suppose that \( \{A_i: i \in I\} \) is a collection of subsets of \( S \), where \( I \) is a nonempty index set. Then
- \( f\left(\bigcup_{i \in I} A_i\right) = \bigcup_{i \in I} f(A_i) \).
- \( f\left(\bigcap_{i \in I} A_i\right) \subseteq \bigcap_{i \in I} f(A_i) \). Equality holds if \( f \) is one-to-one.
Proof
- \( y \in f\left(\bigcup_{i \in I} A_i\right)\) if and only if \( y = f(x) \) for some \( x \in \bigcup_{i \in I} A_i \) if and only if \( y = f(x) \) for some \( x \in A_i \) and some \( i \in I \) if and only if \( y \in f(A_i) \) for some \( i \in I \) if and only if \(y \in \bigcup_{i \in I} f(A_i)\).
- If \( y \in f\left(\bigcap_{i \in I} A_i\right) \) then \( y = f(x) \) for some \( x \in \bigcap_{i \in I} A_i \). Hence \( x \in A_i \) for every \( i \in I \) so \( y \in f(A_i) \) for every \( i \in I \) and thus \( y \in \bigcap_{i \in I} f(A_i) \). Conversely, suppose that \( y \in \bigcap_{i \in I} f(A_i) \). Then \( y \in f(A_i) \) for every \( i \in I \). Hence for every \( i \in I \) there exists \( x_i \in A_i \) with \( y = f(x_i) \). If \( f \) is one-to-one, \( x_i = x_j \) for all \( i, \, j \in I \). Call the common value \( x \). Then \( x \in A_i \) for every \( i \in I \) so \( x \in \bigcap_{i \in I} A_i \) and therefore \( y \in f\left(\bigcap_{i \in I} A_i\right) \).
Suppose again that \(f: S \to T\). As noted earlier, the forward images of \(f\) define a function from \(\mathscr{P}(S)\) into \(\mathscr{P}(T)\) and the inverse images define a function from \(\mathscr{P}(T)\) into \(\mathscr{P}(S)\). One might hope that these functions are inverses of one another, but alas no.
Suppose that \(f: S \to T\).
- \(A \subseteq f^{-1}\left[f(A)\right]\) for \(A \subseteq S\). Equality holds if \( f \) is one-to-one.
- \(f\left[f^{-1}(B)\right] \subseteq B\) for \(B \subseteq T\). Equality holds if \( f \) is onto.
Proof
- If \( x \in A \) then \( f(x) \in f(A) \) and hence \( x \in f^{-1}\left[f(A)\right] \). Conversely suppose that \( x \in f^{-1}\left[f(A)\right] \). Then \( f(x) \in f(A) \) so \( f(x) = f(u) \) for some \( u \in A \). At this point we can go no further. But if \( f \) is one-to-one, then \( u = x \) and hence \( x \in A \).
- Suppose \( y \in f\left[f^{-1}(B)\right] \). Then \( y = f(x) \) for some \( x \in f^{-1}(B) \). But then \( y = f(x) \in B \). Conversely suppose that \( f \) is onto and \( y \in B \). There exist \( x \in S \) with \( f(x) = y \). Hence \( x \in f^{-1}(B) \) and so \( y \in f\left[f^{-1}(B)\right] \).
Spaces of Real Functions
Real-valued function on a given set \(S\) are of particular importance. The usual arithmetic operations on such functions are defined pointwise.
Suppose that\( f, \, g: S \to \R \) and \( c \in \R \), then \( f + g, \, f - g, \, f g, \, c f, \, f / g: S \to \R\) are defined as follows for all \( x \in S \).
- \( (f + g)(x) = f(x) + g(x) \)
- \( (f - g)(x) = f(x) - g(x) \)
- \( (f g)(x) = f(x) g(x) \)
- \( (c f)(x) = c f(x) \)
- \((f/g)(x) = f(x) / g(x)\) assuming that \(g(x) \ne 0\) for \(x \in S\).
Now let \(\mathscr V\) denote the collection of all functions from the given set \(S\) into \(\R\). A fact that is very important in probability as well as other branches of analysis is that \( \mathscr V \), with addition and scalar multiplication as defined above, is a vector space. The zero function \( \bs 0 \) is defined, of course, by \( \bs{0}(x) = 0 \) for all \( x \in S \).
\( (\mathscr V, +, \cdot) \) is a vector space over \( \R \). That is, for all \( f, \, g, \, h \in \mathscr V \) and \( a, \, b \in \R \)
- \( f + g = g + f \), the commutative property of vector addition.
- \( f + (g + h) = (f + g) + h \), the associative property of vector addition.
- \( a(f + g) = a f + a g \), scalar multiplication distributes over vector addition.
- \( (a + b)f = a f + b f \), scalar multiplication distributive over scalar addition.
- \( f + \bs 0 = f\), the existence of an zero vector.
- \( f + (-f) = \bs 0 \), the existence of additive inverses.
- \( 1 \cdot f = f \), the unity property.
Proof
Each of these properties follows from the corresponding property in \( \R \).
Various subspaces of \( \mathscr V \) are important in probability as well. We will return to the discussion of vector spaces of functions in the sections on partial orders and in the advanced sections on metric spaces and measure theory.
Indicator Functions
For our next discussion, suppose that \(S\) is the universal set, so that all other sets mentioned are subsets of \(S\).
Suppose that \(A \subseteq S\). The indicator function of \(A\) is the function \(\bs{1}_A: S \to \{0, 1\}\) defined as follows: \[ \bs{1}_A(x) = \begin{cases} 1, & x \in A \\ 0, & x \notin A \end{cases} \]
Thus, the indicator function of \( A \) simply indicates whether or not \( x \in A \) for each \( x \in S \). Conversely, any function on \(S\) that just takes the values 0 and 1 is an indicator function.
If \(f: S \to \{0, 1\}\) then \(f\) is the indicator function of the set \(A = f^{-1}\{1\} = \{x \in S: f(x) = 1\}\).
Thus, there is a one-to-one correspondence between \(\mathscr{P}(S)\), the power set of \(S\), and the collection of indicator functions \(\{0, 1\}^S\). The next result shows how the set algebra of subsets corresponds to the arithmetic algebra of the indicator functions.
Suppose that \(A, \, B \subseteq S\). Then
- \(\bs{1}_{A \cap B} = \bs{1}_A \, \bs{1}_B = \min\left\{\bs{1}_A, \bs{1}_B\right\}\)
- \(\bs{1}_{A \cup B} = 1 - \left(1 - \bs{1}_A\right)\left(1 - \bs{1}_B\right) = \max\left\{\bs{1}_A, \bs{1}_B\right\}\)
- \(\bs{1}_{A^c} = 1 - \bs{1}_A\)
- \(\bs{1}_{A \setminus B} = \bs{1}_A \left(1 - \bs{1}_B\right)\)
- \(A \subseteq B\) if and only if \(\bs{1}_A \le \bs{1}_B\)
Proof
- Note that both functions on the right just take the values 0 and 1. Moreover, \( \bs{1}_A(x) \bs{1}_B(x) = \min\left\{\bs{1}_A(x), \bs{1}_B(x)\right\} = 1\) if and only if \( x \in A \) and \( x \in B \).
- Note that both function on the right just take the values 0 and 1. Moreover, \( 1 - \left(1 - \bs{1}_A(x)\right)\left(1 - \bs{1}_B(x)\right) = \max\left\{\bs{1}_A(x), \bs{1}_B(x)\right\} = 1 \) if and only if \( x \in A \) or \( x \in B \).
- Note that \( 1 - \bs{1}_A \) just takes the values 0 and 1. Moreover, \( 1 - \bs{1}_A(x) = 1\) if and only if \( x \notin A \).
- Note that \( \bs{1}_{A \setminus B} = \bs{1}_{A \cap B^c} = \bs{1}_A \bs{1}_{B^c} = \bs{1}_A \left(1 - \bs{1}_B\right) \) by parts (a) and (c).
- Since both functions just take the values 0 and 1, note that \( \bs{1}_A \le \bs{1}_B \) if and only if \( \bs{1}_A(x) = 1 \) implies \( \bs{1}_B(x) = 1 \). But in turn, this is equivalent to \( A \subseteq B \).
The results in part (a) extends to arbitrary intersections and the results in part (b) extends to arbitrary unions.
Suppose that \( \{A_i: i \in I\} \) is a collection of subsets of \( S \), where \( I \) is a nonempty index set. Then
- \( \bs{1}_{\bigcap_{i \in I} A_i} = \prod_{i \in I} \bs{1}_{A_i} = \min\left\{\bs{1}_{A_i}: i \in I\right\} \)
- \( \bs{1}_{\bigcup_{i \in I} A_i} = 1 - \prod_{i \in I}\left(1 - \bs{1}_{A_i}\right) = \max\left\{\bs{1}_{A_i}: i \in I\right\} \)
Proof
In general, a product over an infinite index set may not make sense. But if all of the factors are either 0 or 1, as they are here, then we can simply define the product to be 1 if all of the factors are 1, and 0 otherwise.
- The functions in the middle and on the right just take the values 0 and 1. Moreover, both take the value 1 at \( x \in S \) if and only if \( x \in A_i \) for every \( i \in I \).
- The functions in the middle and on the right just take the values 0 and 1. Moreover, both take the value 1 at \( x \in S \) if and only if \( x \in A_i \) for some \( i \in I \).
Multisets
A multiset is like an ordinary set, except that elements may be repeated. A multiset \( A \) (with elements from a universal set \( S \)) can be uniquely associated with its multiplicity function \( m_A: S \to \N \), where \( m_A(x) \) is the number of times that element \( x \) is in \( A \) for each \( x \in S \). So the multiplicity function of a multiset plays the same role that an indicator function does for an ordinary set. Multisets arise naturally when objects are sampled with replacement (but without regard to order) from a population. Various sampling models are explored in the section on Combinatorial Structures. We will not go into detail about the operations on multisets, but the definitions are straightforward generalizations of those for ordinary sets.
Suppose that \( A \) and \( B \) are multisets with elements from the universal set \( S \). Then
- \( A \subseteq B \) if and only if \( m_A \le m_B \)
- \(m_{A \cup B} = \max\{m_A, m_B\}\)
- \( m_{A \cap B} = \min\{m_A, m_B\} \)
- \( m_{A + B} = m_A + m_B \)
Product Spaces
Using functions, we can generalize the Cartesian products studied earlier. In this discussion, we suppose that \(S_i\) is a set for each \(i\) in a nonempty index set \(I\).
Define the product set \[ \prod_{i \in I} S_i = \left\{x: x \text{ is a function from } I \text{ into } \bigcup_{i \in I} S_i \text{ such that } x(i) \in S_i \text{ for each } i \in I\right\} \]
Note that except for being nonempty, there are no assumptions on the cardinality of the index set \( I \). Of course, if \( I = \{1, 2 \ldots, n\} \) for some \( n \in \N_+ \), or if \( I = \N_+ \) then this construction reduces to \( S_1 \times S_2 \times \cdots \times S_n \) and to \( S_1 \times S_2 \times \cdots \), respectively. Since we want to make the notation more closely resemble that of simple Cartesian products, we will write \( x_i \) instead of \( x(i) \) for the value of the function \( x \) at \( i \in I \), and we sometimes refer to this value as the \( i \)th coordinate of \( x \). Finally, note that if \( S_i = S \) for each \( i \in I \), then \( \prod_{i \in I} S_i \) is simply the set of all functions from \( I \) into \( S \), which we denoted by \( S^I \) above.
For \( j \in I \) define the projection \( p_j: \prod_{i \in I} S_i \to S_j \) by \( p_j(x) = x_j \) for \( x \in \prod_{i \in I} S_i \).
So \( p_j(x) \) is just the \( j \)th coordinate of \( x \). The projections are of basic importance for product spaces. In particular, we have a better way of looking at projections of a subset of a product set.
For \( A \subseteq \prod_{i \in I} S_i \) and \( j \in I \), the forward image \( p_j(A) \) is the projection of \( A \) onto \( S_j \).
Proof
Note that \( p_j(A) = \{p_j(x): x \in A\} = \{x_j: x \in A\} \), the set of all \( j \)th coordinates of the points in \( A \).
So the properties of projection that we studied in the last section are just special cases of the properties of forward images. Projections also allow us to get coordinate functions in a simple way.
Suppose that \( R \) is a set, and that \( f: R \to \prod_{i \in I} S_i \). If \( j \in I \) then \( p_j \circ f : R \to S_j \) is the \( j \)th coordinate function of \( f \).
Proof
Note that for \( x \in R \), \( (p_j \circ f)(x) = p_j[f(x)] = f_j(x) \), the \( j \)th coordinate of \( f(x) \in \prod_{i \in I} S_i \).
This will look more familiar for a simple cartesian product. If \( f: R \to S_1 \times S_2 \times \cdots \times S_n \), then \( f = (f_1, f_2, \ldots, f_n) \) where \( f_j: R \to S_i \) is the \( j \)th coordinate function for \( j \in \{1, 2, \ldots, n\} \).
Cross sections of a subset of a product set can be expressed in terms of inverse images of a function. First we need some additional notation. Suppose that our index set \( I \) has at least two elements. For \( j \in I \) and \( u \in S_j \), define \( j_u : \prod_{i \in I - \{j\}} S_i \to \prod_{i \in I} S_i \) by \( j_u (x) = y \) where \( y_i = x_i \) for \( i \in I - \{j\} \) and \( y_j = u \). In words, \( j_u \) takes a point \( x \in \prod_{i \in I - \{j\}} S_i \) and assigns \( u \) to coordinate \( j \) to produce the point \( y \in \prod_{i \in I} S_i \).
In the setting above, if \( j \in I \), \( u \in S_j \) and \( A \subseteq \prod_{i \in I} S_i \) then \(j_u^{-1}(A)\) is the cross section of \( A \) in the \( j \)th coordinate at \( u \).
Proof
This follows from the definition of cross section: \( j_u^{-1}(A) \) is the set of all \(x \in \prod_{i \in I - \{j\}} S_i \) such that \( y \) defined above is in \( A \) and has \( j \)th coordinate \( u \).
Let's look at this for the product of two sets \( S \) and \( T \). For \( x \in S \), the function \( 1_x: T \to S \times T \) is given by \( 1_x(y) = (x, y) \). Similarly, for \( y \in T \), the function \( 2_y: S \to S \times T \) is given by \( 2_y(x) = (x, y) \). Suppose now that \( A \subseteq S \times T \). If \( x \in S \), then \( 1_x^{-1}(A) = \{y \in T: (x, y) \in A\} \), the very definition of the cross section of \( A \) in the first coordinate at \( x \). Similarly, if \( y \in T \), then \( 2_y^{-1}(A) = \{x \in S: (x, y) \in A\} \), the very definition of the cross section of \( A \) in the second coordinate at \( y \). This construction is not particularly important except to show that cross sections are inverse images. Thus the fact that cross sections preserve all of the set operations is a simple consequence of the fact that inverse images generally preserve set operations.
Operators
Sometimes functions have special interpretations in certain settings.
Suppose that \(S\) is a set.
- A function \(f: S \to S\) is sometimes called a unary operator on \(S\).
- A function \(g: S \times S \to S\) is sometimes called a binary operator on \(S\).
As the names suggests, a unary operator \(f\) operates on an element \(x \in S\) to produce a new element \(f(x) \in S\). Similarly, a binary operator \(g\) operates on a pair of elements \((x, y) \in S \times S\) to produce a new element \(g(x, y) \in S\). The arithmetic operators are quintessential examples:
The following are operators on \(\R\):
- \(\text{minus}(x) = -x\) is a unary operator.
- \(\text{sum}(x, y) = x + y\) is a binary operator.
- \(\text{product}(x, y) = x\,y\) is a binary operator.
- \(\text{difference}(x, y) = x - y\) is a binary operator.
For a fixed universal set \(S\), the set operators studied in the section on Sets provide other examples.
For a given set \(S\), the following are operators on \(\mathscr P(S)\):
- \(\text{complement}(A) = A^c\) is a unary operator.
- \(\text{union}(A, B) = A \cup B\) is a binary operator.
- \(\text{intersect}(A, B) = A \cap B\) is a binary operator.
- \(\text{difference}(A, B) = A \setminus B\) is a binary operator.
As these examples illustrate, a binary operator is often written as \( x \, f \, y \) rather than \( f(x, y) \). Still, it is useful to know that operators are simply functions of a special type.
Suppose that \(f\) is a unary operator on a set \(S\), \(g\) is a binary operator on \(S\), and that \(A \subseteq S\).
- \(A\) is closed under \(f\) if \(x \in A\) implies \(f(x) \in A\).
- \(A\) is closed under \(g\) if \((x, y) \in A \times A\) implies \(g(x, y) \in A\).
Thus if \(A\) is closed under the unary operator \(f\), then \(f\) restricted to \(A\) is unary operator on \(A\). Similary if \(A\) is closed under the binary operator \(g\), then \(g\) restricted to \(A \times A\) is a binary operator on \(A\). Let's return to our most basic example.
For the arithmetic operatoes on \(\R\),
- \(\N\) is closed under plus and times, but not under minus and difference.
- \(\Z\) is closed under plus, times, minus, and difference.
- \( \Q \) is closed under plus, times, minus, and difference.
Many properties that you are familiar with for special operators (such as the arithmetic and set operators) can now be formulated generally.
Suppose that \(f\) and \(g\) are binary operators on a set \(S\). In the following definitions, \(x\), \(y\), and \(z\) are arbitrary elements of \(S\).
- \(f\) is commutative if \(f(x, y) = f(y, x)\), that is, \( x \, f \, y = y \, f \, x \)
- \(f\) is associative if \(f(x, f(y, z)) = f(f(x, y), z)\), that is, \( x \, f \, (y \, f \, z) = (x \, f \, y) \, f \, z \).
- \(g\) distributes over \(f\) (on the left) if \(g(x, f(y, z)) = f(g(x, y), g(x, z))\), that is, \( x \, g \, (y \, f \, z) = (x \, g \, y) \, f \, (x \, g \, z) \)
The Axiom of Choice
Suppose that \(\mathscr{S}\) is a collection of nonempty subsets of a set \(S\). The axiom of choice states that there exists a function \(f: \mathscr{S} \to S\) with the property that \(f(A) \in A\) for each \(A \in \mathscr{S}\). The function \(f\) is known as a choice function.
Stripped of most of the mathematical jargon, the idea is very simple. Since each set \(A \in \mathscr{S}\) is nonempty, we can select an element of \(A\); we will call the element we select \(f(A)\) and thus our selections define a function. In fact, you may wonder why we need an axiom at all. The problem is that we have not given a rule (or procedure or algorithm) for selecting the elements of the sets in the collection. Indeed, we may not know enough about the sets in the collection to define a specific rule, so in such a case, the axiom of choice simply guarantees the existence of a choice function. Some mathematicians, known as constructionists do not accept the axiom of choice, and insist on well defined rules for constructing functions.
A nice consequence of the axiom of choice is a type of duality between one-to-one functions and onto functions.
Suppose that \(f\) is a function from a set \(S\) onto a set \(T\). There exists a one-to-one function \(g\) from \(T\) into \(S\).
Proof.
For each \(y \in T\), the set \(f^{-1}\{y\}\) is non-empty, since \(f\) is onto. By the axiom of choice, we can select an element \(g(y)\) from \(f^{-1}\{y\}\) for each \(y \in T\). The resulting function \(g\) is one-to-one.
Suppose that \(f\) is a one-to-one function from a set \(S\) into a set \(T\). There exists a function \(g\) from \(T\) onto \(S\).
Proof.
Fix a special element \(x_0 \in S\). If \(y \in \text{range}(f)\), there exists a unique \(x \in S\) with \(f(x) = y\). Define \(g(y) = x\). If \(y \notin \text{range}(f)\), define \(g(y) = x_0\). The function \(g\) is onto.
Computational Exercises
Some Elementary Functions
Each of the following rules defines a function from \(\R\) into \(\R\).
- \(f(x) = x^2\)
- \(g(x) = \sin(x)\)
- \(h(x) = \lfloor x \rfloor\)
- \(u(x) = \frac{e^x}{1 + e^x}\)
Find the range of the function and determine if the function is one-to-one in each of the following cases:
- \(f\)
- \(g\)
- \(h\)
- \(u\)
Answer
- Range \([0, \infty)\). Not one-to-one.
- Range \([-1, 1]\). Not one-to-one.
- Range \(\Z\). Not one-to-one.
- Range \((0, 1)\). One-to-one.
Find the following inverse images:
- \(f^{-1}[4, 9]\)
- \(g^{-1}\{0\}\)
- \(h^{-1}\{2, 3, 4\}\)
Answer
- \([-3, -2] \cup [2, 3]\)
- \(\{n \, \pi: n \in \Z\}\)
- \([2, 5)\)
The function \(u\) is one-to-one. Find (that is, give the domain and rule for) the inverse function \(u^{-1}\).
Answer
\(u^{-1}(p) = \ln\left(\frac{p}{1-p}\right)\) for \(p \in (0, 1)\)
Give the rule and find the range for each of the following functions:
- \(f \circ g\)
- \(g \circ f\)
- \(h \circ g \circ f\)
Answer
- \((f \circ g)(x) = \sin^2(x)\). Range \([0, 1]\)
- \((g \circ f)(x) = \sin\left(x^2\right)\). Range \([-1, 1]\)
- \((h \circ g \circ f)(x) = \lfloor \sin(x^2) \rfloor\). Range \(\{-1, 0, 1\}\)
Note that \( f \circ g \) and \( g \circ f \) are well-defined functions from \( \R \) into \( \R \), but \( f \circ g \ne g \circ f \).
Dice
Let \(S = \{1, 2, 3, 4, 5, 6\}^2\). This is the set of possible outcomes when a pair of standard dice are thrown. Let \(f\), \(g\), \( u \), and \( v \) be the functions from \(S\) into \(\Z\) defined by the following rules:
- \(f(x, y) = x + y\)
- \( g(x, y) = y - x \)
- \(u(x, y) = \min\{x, y\}\)
- \(v(x, y) = \max\{x, y\}\)
In addition, let \( F \) and \( U \) be the functions defined by \( F = (f, g) \) and \( U = (u, v) \).
Find the range of each of the following functions:
- \(f\)
- \( g \)
- \(u\)
- \(v\)
- \(U\)
Answer
- \(\{2, 3, 4, \ldots, 12\}\)
- \( \{-5, -4, \ldots, 4, 5\} \)
- \(\{1, 2, 3, 4, 5, 6\}\)
- \(\{1, 2, 3, 4, 5, 6\}\)
- \(\left\{(i, j) \in \{1, 2, 3, 4, 5, 6\}^2: i \le j\right\}\)
Give each of the following inverse images in list form:
- \(f^{-1}\{6\}\)
- \(u^{-1}\{3\}\)
- \(v^{-1}\{4\}\)
- \(U^{-1}\{(3, 4)\}\)
Answer
- \(\{(1,5), (2,4), (3,3), (4,2), (5,1)\}\)
- \(\{(3,3), (3,4), (4,3), (3,5), (5,3), (3,6), (6,3)\}\)
- \(\{(1,4), (4,1), (2,4), (4,2), (3,4), (4,3), (4,4)\}\)
- \(\{(3,4), (4,3)\}\)
Find each of the following compositions:
- \( f \circ U \)
- \( g \circ U \)
- \( u \circ F \)
- \( v \circ F \)
- \( F \circ U \)
- \( U \circ F \)
Answer
- \( f \circ U = f \)
- \( g \circ U = \left|g\right| \)
- \( u \circ F = g \)
- \( v \circ F = f \)
- \( F \circ U = \left(f, \left|g\right|\right) \)
- \( U \circ F = (g, f) \)
Note that while \( f \circ U \) is well-defined, \( U \circ f \) is not. Note also that \( f \circ U = f \) even though \( U \) is not the identity function on \( S \).
Bit Strings
Let \( n \in \N_+ \) and let \( S = \{0, 1\}^n \) and \( T = \{0, 1, \ldots, n\} \). Recall that the elements of \( S \) are bit strings of length \( n \), and could represent the possible outcomes of \( n \) tosses of a coin (where 1 means heads and 0 means tails). Let \( f: S \to T \) be the function defined by \( f(x_1, x_2, \ldots, x_n) = \sum_{i=1}^n x_i \). Note that \( f(\bs{x}) \) is just the number of 1s in the the bit string \( \bs{x} \). Let \( g: T \to S \) be the function defined by \( g(k) = \bs{x}_k \) where \( \bs{x}_k \) denotes the bit string with \( k \) 1s followed by \( n - k \) 0s.
Find each of the following
- \( f \circ g \)
- \( g \circ f \)
Answer
- \( f \circ g: T \to T \) and \( \left(f \circ g\right)(k) = k \).
- \( g \circ f: S \to S \) and \( \left(g \circ f\right)(\bs{x}) = \bs{x}_k \) where \( k = f(\bs{x}) = \sum_{i=1}^n x_i \). In words, \( \left(g \circ f\right)(\bs{x}) \) is the bit string with the same number of 1s as \( \bs{x} \), but rearranged so that all the 1s come first.
In the previous exercise, note that \( f \circ g \) and \( g \circ f \) are both well-defined, but have different domains, and so of course are not the same. Note also that \( f \circ g \) is the identity function on \( T \), but \( f \) is not the inverse of \( g \). Indeed \( f \) is not one-to-one, and so does not have an inverse. However, \( f \) restricted to \( \left\{\bs{x}_k: k \in T\right\} \) (the range of \( g \)) is one-to-one and is the inverse of \( g \).
Let \( n = 4 \). Give \( f^{-1}(\{k\}) \) in list form for each \( k \in T \).
Answer
- \( f^{-1}(\{0\}) = \{0000\} \)
- \( f^{-1}(\{1\}) = \{1000, 0100, 0010, 0001\} \)
- \( f^{-1}(\{2\}) = \{1100, 1010, 1001, 0110, 0101, 0011\} \)
- \( f^{-1}(\{3\}) = \{1110, 1101, 1011, 0111\} \)
- \( f^{-1}(\{4\}) = \{1111\}\)
Again let \( n = 4 \). Let \( A = \{1000, 1010\} \) and \( B = \{1000, 1100\} \). Give each of the following in list form:
- \( f(A) \)
- \( f(B) \)
- \( f(A \cap B) \)
- \( f(A) \cap f(B) \)
- \( f^{-1}\left(f(A)\right) \)
Answer
- \( \{1, 2\} \)
- \( \{1, 2\} \)
- \( \{1\} \)
- \( \{1, 2\} \)
- \( \{1000, 0100, 0010, 0001, 1100, 1010, 1001, 0110, 0101, 0011\} \)
In the previous exercise, note that \( f(A \cap B) \subset f(A) \cap f(B) \) and \(A \subset f^{-1}\left(f(A)\right) \).
Indicator Functions
Suppose that \(A\) and \(B\) are subsets of a universal set \(S\). Express, in terms of \(\bs{1}_A\) and \(\bs{1}_B\), the indicator function of each of the 14 non-trivial sets that can be constructed from \(A\) and \(B\). Use the Venn diagram app to help.
Answer
- \(\bs{1}_A \)
- \(\bs{1}_B \)
- \( \bs{1}_{A^c} = 1 - \bs{1}_A \)
- \( \bs{1}_{B^c} = 1 - \bs{1}_B \)
- \( \bs{1}_{A \cap B} = \bs{1}_A \bs{1}_B \)
- \( \bs{1}_{A \cup B} = \bs{1}_A + \bs{1}_B - \bs{1}_A \bs{1}_B \)
- \( \bs{1}_{A \cap B^c} = \bs{1}_A - \bs{1}_A \bs{1}_B \)
- \( \bs{1}_{B \cap A^c} = \bs{1}_B - \bs{1}_A \bs{1}_B \)
- \( \bs{1}_{A \cup B^c} = 1 - \bs{1}_B + \bs{1}_A \bs{1}_B \)
- \( \bs{1}_{B \cup A^c} = 1 - \bs{1}_A + \bs{1}_A \bs{1}_B \)
- \( \bs{1}_{A^c \cap B^c} = 1 - \bs{1}_A - \bs{1}_B + \bs{1}_A \bs{1}_B \)
- \( \bs{1}_{A^c \cup B^c} = 1 - \bs{1}_A \bs{1}_B \)
- \( \bs{1}_{(A \cap B^c) \cup (B \cap A^c)} = \bs{1}_A + \bs{1}_B - 2 \bs{1}_A \bs{1}_B \)
- \( \bs{1}_{(A \cap B) \cup (A^c \cap B^c)} = 1 - \bs{1}_A - \bs{1}_B + 2 \bs{1}_A \bs{1}_B \)
Suppose that \( A \), \( B \), and \( C \) are subsets of a universal set \( S \). Give the indicator function of each of the following, in terms of \( \bs{1}_A \), \(\bs{1}_B\), and \( \bs{1}_C \) in sum-product form:
- \( D = \{ x \in S: x \text{ is an element of exactly one of the given sets}\} \)
- \( E = \{ x \in S: x \text{ is an element of exactly two of the given sets}\} \)
Answer
- \( \bs{1}_D = \bs{1}_A + \bs{1}_B + \bs{1}_C - 2 \left(\bs{1}_A \bs{1}_B + \bs{1}_A \bs{1}_C + \bs{1}_B \bs{1}_C\right) + 3 \bs{1}_A \bs{1}_B \bs{1}_C \)
- \( \bs{1}_E = \bs{1}_A \bs{1}_B + \bs{1}_A \bs{1}_C + \bs{1}_B \bs{1}_C - 3 \bs{1}_A \bs{1}_B \bs{1}_C \)
Operators
Recall the standard arithmetic operators on \( \R \) discussed above.
We all know that sum is commutative and associative, and that product distributes over sum.
- Is difference commutative?
- Is difference associative?
- Does product distribute over difference?
- Does sum distributed over product?
Answer
- No. \( x - y \ne y - x \)
- No. \( x - (y - z) \ne (x - y) - z \)
- Yes. \( x (y - z) = (x y) - (x z) \)
- No. \( x + (y z) \ne (x + y) (x + z) \)
Multisets
Express the multiset \( A \) in list form that has the multiplicity function \( m: \{a, b, c, d, e\} \to \N \) given by \( m(a) = 2 \), \( m(b) = 3 \), \( m(c) = 1 \), \( m(d) = 0 \), \( m(e) = 4 \).
Answer
\( A = \{a, a, b, b, b, c, e, e, e, e\} \)
Express the prime factors of 360 as a multiset in list form.
Answer
\(\{2, 2, 2, 3, 3, 5\}\)


