10.1: Regression
- Page ID
- 5220
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)When comparing two different variables, two questions come to mind: “Is there a relationship between two variables?” and “How strong is that relationship?” These questions can be answered using regression and correlation. Regression answers whether there is a relationship (again this book will explore linear only) and correlation answers how strong the linear relationship is. To introduce both of these concepts, it is easier to look at a set of data.
Example \(\PageIndex{1}\) if there is a relationship
Is there a relationship between the alcohol content and the number of calories in 12-ounce beer? To determine if there is one a random sample was taken of beer’s alcohol content and calories ("Calories in beer," 2011), and the data is in Example \(\PageIndex{1}\).
| Brand | Brewery | Alcohol Content | Calories in 12 oz |
|---|---|---|---|
| Big Sky Scape Goat Pale Ale | Big Sky Brewing | 4.70% | 163 |
| Sierra Nevada Harvest Ale | Sierra Nevada | 6.70% | 215 |
| Steel Reserve | MillerCoors | 8.10% | 222 |
| O'Doul's | Anheuser Busch | 0.40% | 70 |
| Coors Light | MillerCoors | 4.15% | 104 |
| Genesee Cream Ale | High Falls Brewing | 5.10% | 162 |
| Sierra Nevada Summerfest Beer | Sierra Nevada | 5.00% | 158 |
| Michelob Beer | Anheuser Busch | 5.00% | 155 |
| Flying Dog Doggie Style | Flying Dog Brewery | 4.70% | 158 |
| Big Sky I.P.A. | Big Sky Brewing | 6.20% | 195 |
Solution
To aid in figuring out if there is a relationship, it helps to draw a scatter plot of the data. It is helpful to state the random variables, and since in an algebra class the variables are represented as x and y, those labels will be used here. It helps to state which variable is x and which is y.
State random variables
x = alcohol content in the beer
y = calories in 12 ounce beer
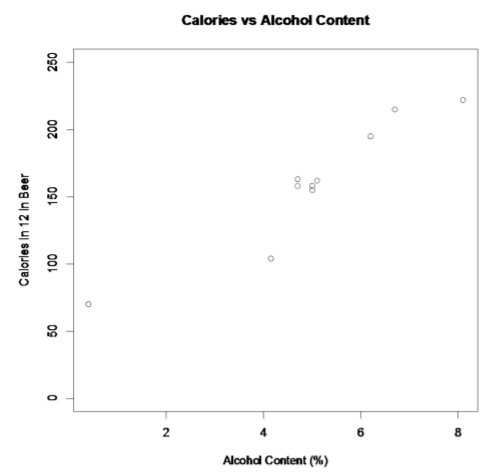.png?revision=1)
This scatter plot looks fairly linear. However, notice that there is one beer in the list that is actually considered a non-alcoholic beer. That value is probably an outlier since it is a non-alcoholic beer. The rest of the analysis will not include O’Doul’s. You cannot just remove data points, but in this case it makes more sense to, since all the other beers have a fairly large alcohol content.
To find the equation for the linear relationship, the process of regression is used to find the line that best fits the data (sometimes called the best fitting line). The process is to draw the line through the data and then find the distances from a point to the line, which are called the residuals. The regression line is the line that makes the square of the residuals as small as possible, so the regression line is also sometimes called the least squares line. The regression line and the residuals are displayed in Figure \(\PageIndex{2}\).
.png?revision=1)
To find the regression equation (also known as best fitting line or least squares line)
Given a collection of paired sample data, the regression equation is
\(\hat{y}=a+b x\)
where the slope = \(b=\dfrac{S S_{\mathrm{xy}}}{S S_{x}}\) and y-intercept = \(a=\overline{y}-b \overline{x}\)
Definition \(\PageIndex{1}\)
The residuals are the difference between the actual values and the estimated values.
residual \(=y-\hat{y}\)
Definition \(\PageIndex{2}\)
SS stands for sum of squares. So you are summing up squares. With the subscript xy, you aren’t really summing squares, but you can think of it that way in a weird sense.
\(\begin{array}{l}{S S_{x y}=\sum(x-\overline{x})(y-\overline{y})} \\ {S S_{x}=\sum(x-\overline{x})^{2}} \\ {S S_{y}=\sum(y-\overline{y})^{2}}\end{array}\)
Note
The easiest way to find the regression equation is to use the technology.
The independent variable, also called the explanatory variable or predictor variable, is the x-value in the equation. The independent variable is the one that you use to predict what the other variable is. The dependent variable depends on what independent value you pick. It also responds to the explanatory variable and is sometimes called the response variable. In the alcohol content and calorie example, it makes slightly more sense to say that you would use the alcohol content on a beer to predict the number of calories in the beer.
Definition \(\PageIndex{3}\)
The population equation looks like:
\(\begin{array}{l}{y=\beta_{o}+\beta_{1} x} \\ {\beta_{o}=\text { slope }} \\ {\beta_{1}=y \text { -intercept }}\end{array}\)
\(\hat{y}\) is used to predict y.
Assumptions of the regression line:
- The set \((x, y)\) of ordered pairs is a random sample from the population of all such possible \((x, y)\) pairs.
- For each fixed value of x, the y-values have a normal distribution. All of the y distributions have the same variance, and for a given x-value, the distribution of y-values has a mean that lies on the least squares line. You also assume that for a fixed y, each x has its own normal distribution. This is difficult to figure out, so you can use the following to determine if you have a normal distribution.
- Look to see if the scatter plot has a linear pattern.
- Examine the residuals to see if there is randomness in the residuals. If there is a pattern to the residuals, then there is an issue in the data.
Example \(\PageIndex{2}\) find the equation of the regression line
- Is there a positive relationship between the alcohol content and the number of calories in 12-ounce beer? To determine if there is a positive linear relationship, a random sample was taken of beer’s alcohol content and calories for several different beers ("Calories in beer," 2011), and the data are in Example \(\PageIndex{2}\).
- Use the regression equation to find the number of calories when the alcohol content is 6.50%.
- Use the regression equation to find the number of calories when the alcohol content is 2.00%.
- Find the residuals and then plot the residuals versus the x-values.
| Brand | Brewery | Alcohol Content | Calories in 12 oz |
|---|---|---|---|
| Big Sky Scape Goat Pale Ale | Big Sky Brewing | 4.70% | 163 |
| Sierra Nevada Harvest Ale | Sierra Nevada | 6.70% | 215 |
| Steel Reserve | MillerCoors | 8.10% | 222 |
| O'Doul's | Anheuser Busch | 0.40% | 70 |
| Coors Light | MillerCoors | 4.15% | 104 |
| Genesee Cream Ale | High Falls Brewing | 5.10% | 162 |
| Sierra Nevada Summerfest Beer | Sierra Nevada | 5.00% | 158 |
| Michelob Beer | Anheuser Busch | 5.00% | 155 |
| Flying Dog Doggie Style | Flying Dog Brewery | 4.70% | 158 |
| Big Sky I.P.A. | Big Sky Brewing | 6.20% | 195 |
Solution
a. State random variables
x = alcohol content in the beer
y = calories in 12 ounce beer
Assumptions check:
- A random sample was taken as stated in the problem.
- The distribution for each calorie value is normally distributed for every value of alcohol content in the beer.
- From Example \(\PageIndex{1}\), the scatter plot looks fairly linear.
- The residual versus the x-values plot looks fairly random. (See Figure \(\PageIndex{5}\).)
It appears that the distribution for calories is a normal distribution.
To find the regression equation on the TI-83/84 calculator, put the x’s in L1 and the y’s in L2. Then go to STAT, over to TESTS, and choose LinRegTTest. The setup is in Figure \(\PageIndex{3}\). The reason that >0 was chosen is because the question was asked if there was a positive relationship. If you are asked if there is a negative relationship, then pick <0. If you are just asked if there is a relationship, then pick \(\neq 0\). Right now the choice will not make a different, but it will be important later.
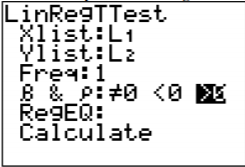.png?revision=1)
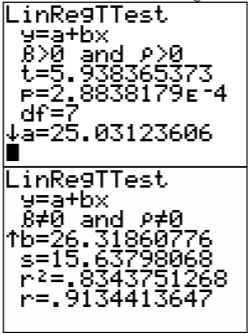.png?revision=1)
From this you can see that
\(\hat{y}=25.0+26.3 x\)
To find the regression equation using R, the command is lm(dependent variable ~ independent variable), where ~ is the tilde symbol located on the upper left of most keyboards. So for this example, the command would be lm(calories ~ alcohol), and the output would be
Call:
lm(formula = calories ~ alcohol)
Coefficients:
(Intercept) alcohol
25.03 26.32
From this you can see that the y-intercept is 25.03 and the slope is 26.32. So the regression equation is \(\hat{y}=25.0+26.3 x\).
Remember, this is an estimate for the true regression. A different random sample would produce a different estimate.
b. \(\begin{array}{l}{x_{o}=6.50} \\ {\hat{y}=25.0+26.3(6.50)=196 \text { calories }}\end{array}\)
If you are drinking a beer that is 6.50% alcohol content, then it is probably close to 196 calories. Notice, the mean number of calories is 170 calories. This value of 196 seems like a better estimate than the mean when looking at the original data. The regression equation is a better estimate than just the mean.
c. \(\begin{array}{l}{x_{o}=2.00} \\ {\hat{y}=25.0+26.3(2.00)=78 \text { calories }}\end{array}\)
If you are drinking a beer that is 2.00% alcohol content, then it has probably close to 78 calories. This doesn’t seem like a very good estimate. This estimate is what is called extrapolation. It is not a good idea to predict values that are far outside the range of the original data. This is because you can never be sure that the regression equation is valid for data outside the original data.
d. To find the residuals, find \(\hat{y}\) for each x-value. Then subtract each \(\hat{y}\) from the given y value to find the residuals. Realize that these are sample residuals since they are calculated from sample values. It is best to do this in a spreadsheet.
| x | y | \(\hat{y}=25.0+26.3 x\) | \(y-\hat{y}\) |
| 4.70 | 163 | 148.61 | 14.390 |
| 6.70 | 215 | 201.21 | 13.790 |
| 8.10 | 222 | 238.03 | -16.030 |
| 4.15 | 104 | 134.145 | -30.145 |
| 5.10 | 162 | 159.13 | 2.870 |
| 5.00 | 158 | 156.5 | 1.500 |
| 5.00 | 155 | 156.5 | -1.500 |
| 4.70 | 158 | 148.61 | 9.390 |
| 6.20 | 195 | 188.06 | 6.940 |
Notice the residuals add up to close to 0. They don’t add up to exactly 0 in this example because of rounding error. Normally the residuals add up to 0.
You can use R to get the residuals. The command is
lm.out = lm(dependent variable ~ independent variable) – this defines the linear model with a name so you can use it later.
Then residual(lm.out) – produces the residuals.
For this example, the command would be
lm(calories~alcohol)
Call:
lm(formula = calories ~ alcohol)
Coefficients:
(Intercept) alcohol
25.03 26.32
> residuals(lm.out)
\(\begin{array}{ccccc}{1} & {2} & {3} & {4} & {5} & {6} & {7} & {8} & {9} \\ {14.271307} & {13.634092} & {-16.211959} & {-30.253458} & {2.743864} & {1.375725} & {-1.624275} & {9.271307} & {6.793396}\end{array}\)
So the first residual is 14.271307 and it belongs to the first x value. The residual 13.634092 belongs to the second x value, and so forth.
You can then graph the residuals versus the independent variable using the plot command. For this example, the command would be plot(alcohol, residuals(lm.out), main="Residuals for Beer Calories versus Alcohol Content", xlab="Alcohol Content", ylab="Residuals"). Sometimes it is useful to see the x-axis on the graph, so after creating the plot, type the command abline(0,0).
The graph of the residuals versus the x-values is in Figure \(\PageIndex{5}\). They appear to be somewhat random.
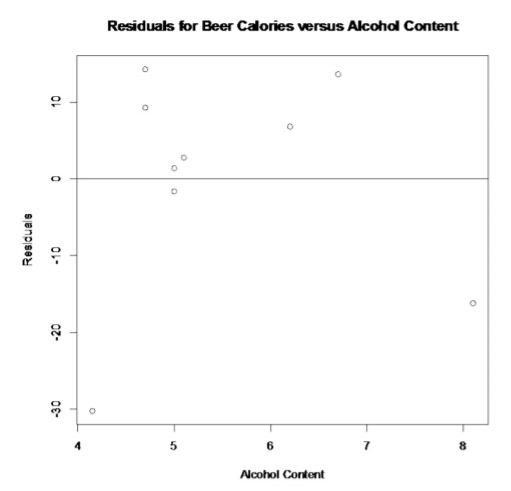.png?revision=1)
Notice, that the 6.50% value falls into the range of the original x-values. The processes of predicting values using an x within the range of original x-values is called interpolating. The 2.00% value is outside the range of original x-values. Using an x-value that is outside the range of the original x-values is called extrapolating. When predicting values using interpolation, you can usually feel pretty confident that that value will be close to the true value. When you extrapolate, you are not really sure that the predicted value is close to the true value. This is because when you interpolate, you know the equation that predicts, but when you extrapolate, you are not really sure that your relationship is still valid. The relationship could in fact change for different x-values.
An example of this is when you use regression to come up with an equation to predict the growth of a city, like Flagstaff, AZ. Based on analysis it was determined that the population of Flagstaff would be well over 50,000 by 1995. However, when a census was undertaken in 1995, the population was less than 50,000. This is because they extrapolated and the growth factor they were using had obviously changed from the early 1990’s. Growth factors can change for many reasons, such as employment growth, employment stagnation, disease, articles saying great place to live, etc. Realize that when you extrapolate, your predicted value may not be anywhere close to the actual value that you observe.
What does the slope mean in the context of this problem?
\(m=\dfrac{\Delta y}{\Delta x}=\dfrac{\Delta \text { calories }}{\Delta \text { alcohol content }}=\dfrac{26.3 \text { calories }}{1 \%}\)
The calories increase 26.3 calories for every 1% increase in alcohol content.
The y-intercept in many cases is meaningless. In this case, it means that if a drink has 0 alcohol content, then it would have 25.0 calories. This may be reasonable, but remember this value is an extrapolation so it may be wrong.
Consider the residuals again. According to the data, a beer with 6.7% alcohol has 215 calories. The predicted value is 201 calories.
Residual = actual - predicted
=215 - 201
=14
This deviation means that the actual value was 14 above the predicted value. That isn’t that far off. Some of the actual values differ by a large amount from the predicted value. This is due to variability in the dependent variable. The larger the residuals the less the model explains the variability in the dependent variable. There needs to be a way to calculate how well the model explains the variability in the dependent variable. This will be explored in the next section.
The following example demonstrates the process to go through when using the formulas for finding the regression equation, though it is better to use technology. This is because if the linear model doesn’t fit the data well, then you could try some of the other models that are available through technology.
Example \(\PageIndex{3}\) calculating the regression equation with the formula
Is there a relationship between the alcohol content and the number of calories in 12-ounce beer? To determine if there is one a random sample was taken of beer’s alcohol content and calories ("Calories in beer," 2011), and the data are in Example \(\PageIndex{2}\). Find the regression equation from the formula.
Solution
State random variables
x = alcohol content in the beer
y = calories in 12 ounce beer
| Alcohol Content | Calories | \(x-\overline{x}\) | \(y-\overline{y}\) | \((x-\overline{x})^{2}\) | \((y-\overline{y})^{2}\) | \((x-\overline{x})(y-\overline{y})\) |
|---|---|---|---|---|---|---|
| 4.70 | 163 | -0.8167 | -7.2222 | 0.6669 | 52.1065 | 5.8981 |
| 6.70 | 215 | 1.1833 | 44.7778 | 1.4003 | 2005.0494 | 52.9870 |
| 8.10 | 222 | 2.5833 | 51.7778 | 6.6736 | 2680.9383 | 133.7595 |
| 4.15 | 104 | -1.3667 | -66.2222 | 1.8678 | 4385.3827 | 90.5037 |
| 5.10 | 162 | -0.4167 | -8.2222 | 0.1736 | 67.6049 | 3.4259 |
| 5.00 | 158 | -0.5167 | -12.2222 | 0.2669 | 149.3827 | 6.3148 |
| 5.00 | 155 | -0.5167 | -15.2222 | 0.2669 | 231.7160 | 7.8648 |
| 4.70 | 158 | -0.8167 | -12.2222 | 0.6669 | 149.3827 | 9.9815 |
| 6.20 | 195 | 0.6833 | 24.7778 | 0.4669 | 613.9383 | 16.9315 |
| 5.516667 = \(\overline{x}\) | 170.2222 = \(\overline{y}\) | 12.45 = \(S S_{x}\) | 10335.5556 = \(S S_{y}\) | 327.6667 = \(S S_{xy}\) |
slope: \(b=\dfrac{S S_{x y}}{S S_{x}}=\dfrac{327.6667}{12.45} \approx 26.3\)
y-intercept: \(a=\overline{y}-b \overline{x}=170.222-26.3(5.516667) \approx 25.0\)
Regression equation: \(\hat{y}=25.0+26.3 x\)
Homework
Exercise \(\PageIndex{1}\)
For each problem, state the random variables. Also, look to see if there are any outliers that need to be removed. Do the regression analysis with and without the suspected outlier points to determine if their removal affects the regression. The data sets in this section are used in the homework for sections 10.2 and 10.3 also.
- When an anthropologist finds skeletal remains, they need to figure out the height of the person. The height of a person (in cm) and the length of their metacarpal bone 1 (in cm) were collected and are in Example \(\PageIndex{5}\) ("Prediction of height," 2013). Create a scatter plot and find a regression equation between the height of a person and the length of their metacarpal. Then use the regression equation to find the height of a person for a metacarpal length of 44 cm and for a metacarpal length of 55 cm. Which height that you calculated do you think is closer to the true height of the person? Why?
Length of Metacarpal (cm) Height of Person (cm) 45 171 51 178 39 157 41 163 48 172 49 183 46 173 43 175 47 173 Table \(\PageIndex{5}\): Data of Metacarpal versus Height - Example \(\PageIndex{6}\) contains the value of the house and the amount of rental income in a year that the house brings in ("Capital and rental," 2013). Create a scatter plot and find a regression equation between house value and rental income. Then use the regression equation to find the rental income a house worth $230,000 and for a house worth $400,000. Which rental income that you calculated do you think is closer to the true rental income? Why?
Value Rental Value Rental Value Rental Value Rental 81000 6656 77000 4576 75000 7280 67500 6864 95000 7904 94000 8736 90000 6240 85000 7072 121000 12064 115000 7904 110000 7072 104000 7904 135000 8320 130000 9776 126000 6240 125000 7904 145000 8320 140000 9568 140000 9152 135000 7488 165000 13312 165000 8528 155000 7488 148000 8320 178000 11856 174000 10400 170000 9568 170000 12688 200000 12272 200000 10608 194000 11232 190000 8320 214000 8528 208000 10400 200000 10400 200000 8320 240000 10192 240000 12064 240000 11648 225000 12480 289000 11648 270000 12896 262000 10192 244500 11232 325000 12480 310000 12480 303000 12272 300000 12480 Table \(\PageIndex{6}\): Data of House Value versus Rental - The World Bank collects information on the life expectancy of a person in each country ("Life expectancy at," 2013) and the fertility rate per woman in the country ("Fertility rate," 2013). The data for 24 randomly selected countries for the year 2011 are in Example \(\PageIndex{7}\). Create a scatter plot of the data and find a linear regression equation between fertility rate and life expectancy. Then use the regression equation to find the life expectancy for a country that has a fertility rate of 2.7 and for a country with fertility rate of 8.1. Which life expectancy that you calculated do you think is closer to the true life expectancy? Why?
Fertility Rate Life Expectancy 1.7 77.2 5.8 55.4 2.2 69.9 2.1 76.4 1.8 75.0 2.0 78.2 2.6 73.0 2.8 70.8 1.4 82.6 2.6 68.9 1.5 81.0 6.9 54.2 2.4 67.1 1.5 73.3 2.5 74.2 1.4 80.7 2.9 72.1 2.1 78.3 4.7 62.9 6.8 54.4 5.2 55.9 4.2 66.0 1.5 76.0 3.9 72.3 Table \(\PageIndex{7}\): Data of Fertility Rates versus Life Expectancy - The World Bank collected data on the percentage of GDP that a country spends on health expenditures ("Health expenditure," 2013) and also the percentage of women receiving prenatal care ("Pregnant woman receiving," 2013). The data for the countries where this information are available for the year 2011 is in Example \(\PageIndex{8}\). Create a scatter plot of the data and find a regression equation between percentage spent on health expenditure and the percentage of women receiving prenatal care. Then use the regression equation to find the percent of women receiving prenatal care for a country that spends 5.0% of GDP on health expenditure and for a country that spends 12.0% of GDP. Which prenatal care percentage that you calculated do you think is closer to the true percentage? Why?
Health Expenditure (% of GDP) Prenatal Care (%) 9.6 47.9 3.7 54.6 5.2 93.7 5.2 84.7 10.0 100.0 4.7 42.5 4.8 96.4 6.0 77.1 5.4 58.3 4.8 95.4 4.1 78.0 6.0 93.3 9.5 93.3 6.8 93.7 6.1 89.8 Table \(\PageIndex{8}\): Data of Health Expenditure versus Prenatal Care - The height and weight of baseball players are in Example \(\PageIndex{9}\) ("MLB heightsweights," 2013). Create a scatter plot and find a regression equation between height and weight of baseball players. Then use the regression equation to find the weight of a baseball player that is 75 inches tall and for a baseball player that is 68 inches tall. Which weight that you calculated do you think is closer to the true weight? Why?
Height (inches) Weight (pounds) 76 212 76 224 72 180 74 210 75 215 71 200 77 235 78 235 77 194 76 185 72 180 72 170 75 220 74 228 73 210 72 180 70 185 73 190 71 186 74 200 74 200 75 210 79 240 72 208 75 180 Table \(\PageIndex{9}\): Heights and Weights of Baseball Players - Different species have different body weights and brain weights are in Example \(\PageIndex{10}\). ("Brain2bodyweight," 2013). Create a scatter plot and find a regression equation between body weights and brain weights. Then use the regression equation to find the brain weight for a species that has a body weight of 62 kg and for a species that has a body weight of 180,000 kg. Which brain weight that you calculated do you think is closer to the true brain weight? Why?
Species Body Weight (kg) Brain Weight (kg) Newborn Human 3.20 0.37 Adult Human 73.00 1.35 Pithecanthropus Man 70.00 0.93 Squirrel 0.80 0.01 Hamster 0.15 0.00 Chimpanzee 50.00 0.42 Rabbit 1.40 0.01 Dog (Beagle) 10.00 0.07 Cat 4.50 0.03 Rat 0.40 0.00 Bottle-Nosed Dolphin 400.00 1.50 Beaver 24.00 0.04 Gorilla 320.00 0.50 Tiger 170.00 0.26 Owl 1.50 0.00 Camel 550.00 0.76 Elephant 4600.00 6.00 Lion 187.00 0.24 Sheep 120.00 0.14 Walrus 800.00 0.93 Horse 450.00 0.50 Cow 700.00 0.44 Giraffe 950.00 0.53 Green Lizard 0.20 0.00 Sperm Whale 35000.00 7.80 Turtle 3.00 0.00 Alligator 270.00 0.01 Table \(\PageIndex{10}\): Body Weights and Brain Weights of Species - A random sample of beef hotdogs was taken and the amount of sodium (in mg) and calories were measured. ("Data hotdogs," 2013) The data are in Example \(\PageIndex{11}\). Create a scatter plot and find a regression equation between amount of calories and amount of sodium. Then use the regression equation to find the amount of sodium a beef hotdog has if it is 170 calories and if it is 120 calories. Which sodium level that you calculated do you think is closer to the true sodium level? Why?
Calories Sodium 186 495 181 477 176 425 149 322 184 482 190 587 158 370 139 322 175 479 148 375 152 330 111 300 141 386 153 401 190 645 157 440 131 317 149 319 135 298 132 253 Table \(\PageIndex{11}\): Calories and Sodium Levels in Beef Hotdogs - Per capita income in 1960 dollars for European countries and the percent of the labor force that works in agriculture in 1960 are in Example \(\PageIndex{12}\) ("OECD economic development," 2013). Create a scatter plot and find a regression equation between percent of labor force in agriculture and per capita income. Then use the regression equation to find the per capita income in a country that has 21 percent of labor in agriculture and in a country that has 2 percent of labor in agriculture. Which per capita income that you calculated do you think is closer to the true income? Why?
Country Percent in Agriculture Per Capita Income Sweden 14 1644 Switzerland 11 1361 Luxembourg 15 1242 U. Kingdom 4 1105 Denmark 18 1049 W. Germany 15 1035 France 20 1013 Belgium 6 1005 Norway 20 977 Iceland 25 839 Netherlands 11 810 Austria 23 681 Ireland 36 529 Italy 27 504 Greece 56 324 Spain 42 290 Portugal 44 238 Turkey 79 177 Table \(\PageIndex{12}\): Percent of Labor in Agriculture and Per Capita Income for European Countries - Cigarette smoking and cancer have been linked. The number of deaths per one hundred thousand from bladder cancer and the number of cigarettes sold per capita in 1960 are in Example \(\PageIndex{13}\) ("Smoking and cancer," 2013). Create a scatter plot and find a regression equation between cigarette smoking and deaths of bladder cancer. Then use the regression equation to find the number of deaths from bladder cancer when the cigarette sales were 20 per capita and when the cigarette sales were 6 per capita. Which number of deaths that you calculated do you think is closer to the true number? Why?
Cigarette Sales (per Capita) Bladder Cancer Deaths (per 100 thousand) Cigarette Sales (per Capita) Bladder Cancer Deaths (per 100 Thousand) 18.20 2.90 42.40 6.54 25.82 3.52 28.64 5.98 18.24 2.99 21.16 2.90 28.60 4.46 29.14 5.30 31.10 5.11 19.96 2.89 33.60 4.78 26.38 4.47 40.46 5.60 23.44 2.93 28.27 4.46 23.78 4.89 20.10 3.08 29.18 4.99 27.91 4.75 18.06 3.25 26.18 4.09 20.94 3.64 22.12 4.23 20.08 2.94 21.84 2.91 22.57 3.21 23.44 2.86 14.00 3.31 21.58 4.65 25.89 4.63 28.92 4.79 21.17 4.04 25.91 5.21 21.25 5.14 26.92 4.69 22.86 4.78 24.96 5.27 28.04 3.20 22.06 3.72 30.34 3.46 16.08 3.06 23.75 3.95 27.56 4.04 23.32 3.72 Table \(\PageIndex{13}\): Number of Cigarettes and Number of Bladder Cancer Deaths in 1960 - The weight of a car can influence the mileage that the car can obtain. A random sample of cars’ weights and mileage was collected and are in Example \(\PageIndex{14}\) ("Passenger car mileage," 2013). Create a scatter plot and find a regression equation between weight of cars and mileage. Then use the regression equation to find the mileage on a car that weighs 3800 pounds and on a car that weighs 2000 pounds. Which mileage that you calculated do you think is closer to the true mileage? Why?
Weight (100 pounds) Mileage (mpg) 22.5 53.3 22.5 41.1 22.5 38.9 25.0 40.9 27.5 46.9 27.5 36.3 30.0 32.2 30.0 32.2 30.0 31.5 30.0 31.4 30.0 31.4 35.0 32.6 35.0 31.3 35.0 31.3 35.0 28.0 35.0 28.0 35.0 28.0 40.0 23.6 40.0 23.6 40.0 23.4 40.0 23.1 45.0 19.5 45.0 17.2 45.0 17.0 55.0 13.2 Table \(\PageIndex{14}\): Weights and Mileages of Cars
- Answer
-
For regression, only the equation is given. See solutions for the entire answer.
1. \(\hat{y}=1.719 x+93.709\)
3. \(\hat{y}=-4.706 x+84.873\)
5. \(\hat{y}=5.859 x-230.942\)
7. \(\hat{y}=4.0133 x-228.3313\)
9. \(\hat{y}=0.12182 x+1.08608\)


