4.4: Counting Techniques

There are times when the sample space or event space are very large, that it isn’t feasible to write it out. In that case, it helps to have mathematical tools for counting the size of the sample space and event space. These tools are known as counting techniques.

Definition \(\PageIndex{1}\)

Multiplication Rule in Counting Techniques

If task 1 can be done \(m_{1}\) ways, task 2 can be done \(m_{2}\) ways, and so forth to task n being done \(m_{n}\) ways. Then the number of ways to do task 1, 2,…, n together would be \(m_{1}^{*} m_{2}^{*} \stackrel{\Delta *}{r} m_{n}\).

Example \(\PageIndex{1}\) multiplication rule in counting

A menu offers a choice of 3 salads, 8 main dishes, and 5 desserts. How many different meals consisting of one salad, one main dish, and one dessert are possible?

Solution

There are three tasks, picking a salad, a main dish, and a dessert. The salad task can be done 3 ways, the main dish task can be done 8 ways, and the dessert task can be done 5 ways. The ways to pick a salad, main dish, and dessert are

\(\dfrac{3}{\text { salad }} \dfrac{8}{\text { main }} \dfrac{5}{\text { dessert }}=120\) different meals

Example \(\PageIndex{2}\) Multiplication rule in counting

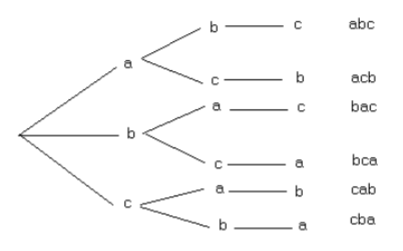
How many three letter “words” can be made from the letters a, b, and c with no letters repeating? A “word” is just an ordered group of letters. It doesn’t have to be a real word in a dictionary.

Solution

There are three tasks that must be done in this case. The tasks are to pick the first letter, then the second letter, and then the third letter. The first task can be done 3 ways since there are 3 letters. The second task can be done 2 ways, since the first task took one of the letters. The third task can be done 1 ways, since the first and second task took two of the letters. There are

\(\dfrac{3}{\text { first letter }} * \dfrac{2}{\text { second letter }} * \dfrac{1}{\text { third letter }}\)

Which is

\(3^{*} 2^{*} 1=6\)

You can also look at this in a tree diagram:

Figure \(\PageIndex{1}\): Tree diagram

So, there are 6 different “words.”

In Example \(\PageIndex{2}\), the solution was found by find \(3*2*1=6\). Many counting problems involve multiplying a list of decreasing numbers. This is called a factorial. There is a special symbol for this and a special button on your calculator.

Definition \(\PageIndex{2}\)

Factorial

\(n !=n(n-1)(n-2) \cdots(3)(2)(1)\)

As an example:

\(5 !=5 * 4 * 3 * 2 * 1=120\)

\(8 !=8 * 7 * 6 * 5 * 4 * 3 * 2 * 1=40320\)

0 factorial is defined to be 0!=1 and 1 factorial is defined to be 1!=1.

Sometimes you are trying to select r objects from n total objects. The number of ways to do this depends on if the order you choose the r objects matters or if it doesn’t. As an example if you are trying to call a person on the phone, you have to have their number in the right order. Otherwise, you call someone you didn’t mean to. In this case, the order of the numbers matters. If however you were picking random numbers for the lottery, it doesn’t matter which number you pick first. As long as you have the same numbers that the lottery people pick, you win. In this case the order doesn’t matter. A permutation is an arrangement of items with a specific order. You use permutations to count items when the order matters. When the order doesn’t matter you use combinations. A combination is an arrangement of items when order is not important. When you do a counting problem, the first thing you should ask yourself is “does order matter?”

Definition \(\PageIndex{3}\)

Permutation Formula

Picking r objects from n total objects when order matters

\(_{n} P_{r}=\dfrac{n !}{(n-r) !}\)

Definition \(\PageIndex{4}\)

Combination Formula

Picking r objects from n total objects when order doesn’t matter

\(_{n} C_{r}=\dfrac{n !}{r !(n-r) !}\)

Example \(\PageIndex{3}\) calculating the number of ways

In a club with 15 members, how many ways can a slate of 3 officers consisting of a president, vice-president, and secretary/treasurer be chosen?

Solution

In this case the order matters. If you pick person 1 for president, person 2 for vice-president, and person 3 for secretary/treasurer you would have different officers than if you picked person 2 for president, person 1 for vice-president, and person 3 for secretary/treasurer. This is a permutation problem with n=15 and r=3.

\(_{15} P_{3}=\dfrac{15 !}{(15-3) !}=\dfrac{15 !}{12 !}=2730\)

Example \(\PageIndex{4}\) calculating the number of ways

Suppose you want to pick 7 people out of 20 people to take part in a survey. How many ways can you do this?

Solution

In this case the order doesn’t matter, since you just want 7 people. This is a combination with n=20 and r=7.

\(_{20} C_{7}=\dfrac{20 !}{7 !(20-7) !}=\dfrac{20 !}{7 ! 13 !}=77520\)

Most calculators have a factorial button on them, and many have the combination and permutation functions also. R has a combination command.

Homework

Exercise \(\PageIndex{1}\)

1. You are going to a benefit dinner, and need to decide before the dinner what you want for salad, main dish, and dessert. You have 2 different salads to choose from, 3 main dishes, and 5 desserts. How many different meals are available?
2. How many different phone numbers are possible in the area code 928?
3. You are opening a T-shirt store. You can have long sleeves or short sleeves, three different colors, five different designs, and four different sizes. How many different shirts can you make?
4. The California license plate has one number followed by three letters followed by three numbers. How many different license plates are there?
5. Find \(_{9} P_{4}\)
6. Find \(_{10} P_{6}\)
7. Find \(_{10} P_{5}\)
8. Find \(_{20} P_{4}\)
9. You have a group of twelve people. You need to pick a president, treasurer, and secretary from the twelve. How many different ways can you do this?
10. A baseball team has a 25-man roster. A batting order has nine people. How many different batting orders are there?
11. An urn contains five red balls, seven yellow balls, and eight white balls. How many different ways can you pick two red balls?
12. How many ways can you choose seven people from a group of twenty?

Answer

1. 30 meals

3. 120 shirts

5. 3024

7. 252

9. 1320

11. 10

Data sources

Aboriginal deaths in custody. (2013, September 26). Retrieved from http://www.statsci.org/data/oz/custody.html

Activities of dolphin groups. (2013, September 26). Retrieved from http://www.statsci.org/data/general/dolpacti.html

Car preferences. (2013, September 26). Retrieved from http://www.statsci.org/data/oz/carprefs.html

Encyclopedia Titanica. (2013, November 09). Retrieved from www.encyclopediatitanica.org/

Leprosy: Number of reported cases by country. (2013, September 04). Retrieved from http://apps.who.int/gho/data/node.main.A1639

Madison, J. (2013, October 15). M&M's color distribution analysis. Retrieved from http://joshmadison.com/2007/12/02/mm...tion-analysis/