3.2: Measures of Spread
- Page ID
- 5172
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Variability is an important idea in statistics. If you were to measure the height of everyone in your classroom, every observation gives you a different value. That means not every student has the same height. Thus there is variability in people’s heights. If you were to take a sample of the income level of people in a town, every sample gives you different information. There is variability between samples too. Variability describes how the data are spread out. If the data are very close to each other, then there is low variability. If the data are very spread out, then there is high variability. How do you measure variability? It would be good to have a number that measures it. This section will describe some of the different measures of variability, also known as variation.
In Example \(\PageIndex{1}\), the average weight of a cat was calculated to be 8.02 pounds. How much does this tell you about the weight of all cats? Can you tell if most of the weights were close to 8.02 or were the weights really spread out? What are the highest weight and the lowest weight? All you know is that the center of the weights is 8.02 pounds. You need more information.
Definition \(\PageIndex{1}\)
The range of a set of data is the difference between the highest and the lowest data values (or maximum and minimum values).
\[\begin{align*} \text{Range} &= \text{highest value} - \text{lowest value} \\[4pt] &= \text{maximum value} - \text{minimum value} \end{align*}\]
Example \(\PageIndex{1}\): Finding the Range
Look at the following three sets of data. Find the range of each of these.
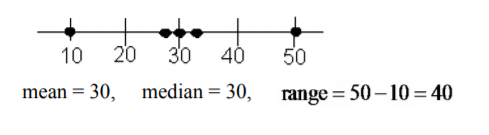
- \(10, 20, 30, 40, 50\)
- \(10, 29, 30, 31, 50\)
- \(28, 29, 30, 31, 32\)
Solution
a.
.png?revision=1)
b.
.png?revision=1)
c.
.png?revision=1)
Based on the mean, median, and range in Example \(\PageIndex{1}\), the first two distributions are the same, but you can see from the graphs that they are different. In Example \(\PageIndex{1}\)a the data are spread out equally. In Example \(\PageIndex{1}\)b the data has a clump in the middle and a single value at each end. The mean and median are the same for Example \(\PageIndex{1}\)c but the range is very different. All the data is clumped together in the middle.
The range doesn’t really provide a very accurate picture of the variability. A better way to describe how the data is spread out is needed. Instead of looking at the distance the highest value is from the lowest how about looking at the distance each value is from the mean. This distance is called the deviation.
Example \(\PageIndex{2}\): Finding the Deviations
Suppose a vet wants to analyze the weights of cats. The weights (in pounds) of five cats are 6.8, 8.2, 7.5, 9.4, and 8.2. Find the deviation for each of the data values.
Solution
Variable: \(x=\) weight of a cat
The mean for this data set is \(\overline{x}=8.02\) pounds.
| \(x\) | \(x-\overline{x}\) |
|---|---|
| 6.8 | 6.8-8.02 = -1.22 |
| 8.2 | 8.2-8.02=0.18 |
| 7.5 | 7.5-8.02=-0.52 |
| 9.4 | 9.4-8.02=1.38 |
| 8.2 | 8.2-8.02=0.18 |
Now you might want to average the deviation, so you need to add the deviations together.
| \(x\) | \(x-\overline{x}\) |
|---|---|
| 6.8 | 6.8-8.02 = -1.22 |
| 8.2 | 8.2-8.02=0.18 |
| 7.5 | 7.5-8.02=-0.52 |
| 9.4 | 9.4-8.02=1.38 |
| 8.2 | 8.2-8.02=0.18 |
| Total | 0 |
This can’t be right. The average distance from the mean cannot be 0. The reason it adds to 0 is because there are some positive and negative values. You need to get rid of the negative signs. How can you do that? You could square each deviation.
| \(x\) | \(x-\overline{x}\) | \((x-\overline{x})^{2}\) |
|---|---|---|
| 6.8 | 6.8-8.02 = -1.22 | 1.4884 |
| 8.2 | 8.2-8.02=0.18 | 0.0324 |
| 7.5 | 7.5-8.02=-0.52 | 0.2704 |
| 9.4 | 9.4-8.02=1.38 | 1.9044 |
| 8.2 | 8.2-8.02=0.18 | 0.0324 |
| Total | 0 | 3.728 |
Now average the total of the squared deviations. The only thing is that in statistics there is a strange average here. Instead of dividing by the number of data values you divide by the number of data values minus 1. In this case you would have
\(s^{2}=\dfrac{3.728}{5-1}=\dfrac{3.728}{4}=0.932 \text { pounds }^{2}\)
Notice that this is denoted as \(s^{2}\). This is called the variance and it is a measure of the average squared distance from the mean. If you now take the square root, you will get the average distance from the mean. This is called the standard deviation, and is denoted with the letter \(s\).
\(s=\sqrt{.932} \approx 0.965\) pounds
The standard deviation is the average (mean) distance from a data point to the mean. It can be thought of as how much a typical data point differs from the mean.
Definition \(\PageIndex{2}\): Sample Variance
The sample variance formula:
\(s^{2}=\dfrac{\sum(x-\overline{x})^{2}}{n-1}\)
where \(\overline{x}\) is the sample mean, \(n\) is the sample size, and \(\sum\) means to find the sum.
Definition \(\PageIndex{3}\): Sample Standard Deviation
The sample standard deviation formula:
\(s=\sqrt{s^{2}}=\sqrt{\dfrac{\sum(x-\overline{x})^{2}}{n-1}}\)
The \(n-1\) on the bottom has to do with a concept called degrees of freedom. Basically, it makes the sample standard deviation a better approximation of the population standard deviation.
Definition \(\PageIndex{4}\): Population Variance
The population variance formula:
\(\sigma^{2}=\dfrac{\sum(x-\mu)^{2}}{N}\)
where \(\sigma\) is the Greek letter sigma and \(\sigma^{2}\) represents the population variance, \(\mu\) is the population mean, and N is the size of the population.
Definition \(\PageIndex{5}\): Population Standard Deviation
The population standard deviation formula:
\(\sigma=\sqrt{\sigma^{2}}=\sqrt{\dfrac{\sum(x-\mu)^{2}}{N}}\)
Note
The sum of the deviations should always be 0. If it isn’t, then it is because you rounded, you used the median instead of the mean, or you made an error. Try not to round too much in the calculations for standard deviation since each rounding causes a slight error
Example \(\PageIndex{3}\): Finding the Standard Deviation
Suppose that a manager wants to test two new training programs. He randomly selects 5 people for each training type and measures the time it takes to complete a task after the training. The times for both trainings are in Example \(\PageIndex{4}\). Which training method is better?
| Training 1 | 56 | 75 | 48 | 63 | 59 |
| Training 2 | 60 | 58 | 66 | 59 | 58 |
Solution
It is important that you define what each variable is since there are two of them.
Variable 1: \(X_{1}=\) productivity from training 1
Variable 2: \(X_{2}=\) productivity from training 2
To answer which training method better, first you need some descriptive statistics. Start with the mean for each sample.
\(\overline{x}_{1}=\dfrac{56+75+48+63+59}{5}=60.2\) minutes
\(\overline{x}_{2}=\dfrac{60+58+66+59+58}{5}=60.2\) minutes
Since both means are the same values, you cannot answer the question about which is better. Now calculate the standard deviation for each sample.
| \(x_{1}\) | \(x_{1}-\overline{x}_{1}\) | \(\left(x_{1}-\overline{x}_{1}\right)^{2}\) |
|---|---|---|
| 56 | -4.2 | 17.64 |
| 75 | 14.8 | 219.04 |
| 48 | -12.2 | 148.84 |
| 63 | 2.8 | 7.84 |
| 59 | -1.2 | 1.44 |
| Total | 0 | 394.8 |
| \(x_{2}\) | \(x_{2}-\overline{x}_{2}\) | \(\left(x_{2}-\overline{x}_{2}\right)^{2}\) |
|---|---|---|
| 60 | -0.2 | 0.04 |
| 58 | -2.2 | 4.84 |
| 66 | 5.8 | 33.64 |
| 59 | -1.2 | 1.44 |
| 58 | -2.2 | 4.84 |
| Total | 0 | 44.8 |
The variance for each sample is:
\(s_{1}^{2}=\dfrac{394.8}{5-1}=98.7 \text { minutes }^{2}\)
\(s_{2}^{2}=\dfrac{44.8}{5-1}=11.2 \text { minutes }^{2}\)
The standard deviations are:
\(s_{1}=\sqrt{98.7} \approx 9.93\) minutes
\(s_{2}=\sqrt{11.2} \approx 3.35\) minutes
From the standard deviations, the second training seemed to be the better training since the data is less spread out. This means it is more consistent. It would be better for the managers in this case to have a training program that produces more consistent results so they know what to expect for the time it takes to complete the task.
You can do the calculations for the descriptive statistics using the technology. The procedure for calculating the sample mean ( \(\overline{x}) \) and the sample standard deviation ( \(s_{x}\)) for \(X_{2}\) in Example \(\PageIndex{3}\) on the TI-83/84 is in Figures 3.2.1 through 3.2.4 (the procedure is the same for \(X_{1}\)). Note the calculator gives you the population standard deviation ( \(\sigma_{x}\) ) because it doesn’t know whether the data you input is a population or a sample. You need to decide which value you need to use, based on whether you have a population or sample. In almost all cases you have a sample and will be using \(s_{x}\). Also, the calculator uses the notation \(s_{x}\) of instead of just \(s\). It is just a way for it to denote the information. First you need to go into the STAT menu, and then Edit. This will allow you to type in your data (see Figure \(\PageIndex{1}\)).
.png?revision=1)
Once you have the data into the calculator, you then go back to the STAT menu, move over to CALC, and then choose 1-Var Stats (see Figure \(\PageIndex{2}\)). The calculator will now put 1-Var Stats on the main screen. Now type in L2 (2nd button and 2) and then press ENTER. (Note if you have the newer operating system on the TI-84, then the procedure is slightly different.) The results from the calculator are in Figure \(\PageIndex{4}\).
.png?revision=1)
.png?revision=1)
.png?revision=1)
The processes for finding the mean, median, range, standard deviation, and variance on R are as follows:
variable<-c(type in your data)
To find the mean, use mean(variable)
To find the median, use median(variable)
To find the range, use range(variable). Then find maximum – minimum.
To find the standard deviation, use sd(variable)
To find the variance, use var(variable)
For the second data set in Example \(\PageIndex{3}\), the commands and results would be
productivity_2<-c(60, 58, 66, 59, 58)
mean(productivity_2)
[1] 60.2
median(productivity_2)
[1] 59
range(productivity_2)
[1] 58 66
sd(productivity_2)
[1] 3.34664
var(productivity_2)
[1] 11.2
In general a “small” standard deviation means the data is close together (more consistent) and a “large” standard deviation means the data is spread out (less consistent). Sometimes you want consistent data and sometimes you don’t. As an example if you are making bolts, you want to lengths to be very consistent so you want a small standard deviation. If you are administering a test to see who can be a pilot, you want a large standard deviation so you can tell who are the good pilots and who are the bad ones.
What do “small” and “large” mean? To a bicyclist whose average speed is 20 mph, s = 20 mph is huge. To an airplane whose average speed is 500 mph, s = 20 mph is nothing. The “size” of the variation depends on the size of the numbers in the problem and the mean. Another situation where you can determine whether a standard deviation is small or large is when you are comparing two different samples such as in example #3.2.3. A sample with a smaller standard deviation is more consistent than a sample with a larger standard deviation.
Many other books and authors stress that there is a computational formula for calculating the standard deviation. However, this formula doesn’t give you an idea of what standard deviation is and what you are doing. It is only good for doing the calculations quickly. It goes back to the days when standard deviations were calculated by hand, and the person needed a quick way to calculate the standard deviation. It is an archaic formula that this author is trying to eradicate it. It is not necessary anymore, since most calculators and computers will do the calculations for you with as much meaning as this formula gives. It is suggested that you never use it. If you want to understand what the standard deviation is doing, then you should use the definition formula. If you want an answer quickly, use a computer or calculator.
Use of Standard Deviation
One of the uses of the standard deviation is to describe how a population is distributed by using Chebyshev’s Theorem. This theorem works for any distribution, whether it is skewed, symmetric, bimodal, or any other shape. It gives you an idea of how much data is a certain distance on either side of the mean.
Definition \(\PageIndex{6}\): Chebyshev's Theorem
For any set of data:
- At least 75% of the data fall in the interval from \(\mu-2 \sigma \text { to } \mu+2 \sigma\).
- At least 88.9% of the data fall in the interval from \(\mu-3 \sigma \text { to } \mu+3 \sigma\).
- At least 93.8% of the data fall in the interval from \(\mu-4 \sigma \text { to } \mu+4 \sigma\).
Example \(\PageIndex{4}\): Using Chebyshev's Theorem
The U.S. Weather Bureau has provided the information in Example \(\PageIndex{7}\) about the total annual number of reported strong to violent (F3+) tornados in the United States for the years 1954 to 2012. ("U.S. tornado climatology," 17).
| 46 | 47 | 31 | 41 | 24 | 56 | 56 | 23 | 31 | 59 |
| 39 | 70 | 73 | 85 | 33 | 38 | 45 | 39 | 35 | 22 |
| 51 | 39 | 51 | 131 | 37 | 24 | 57 | 42 | 28 | 45 |
| 98 | 35 | 54 | 45 | 30 | 15 | 35 | 64 | 21 | 84 |
| 40 | 51 | 44 | 62 | 65 | 27 | 34 | 23 | 32 | 28 |
| 41 | 98 | 82 | 47 | 62 | 21 | 31 | 29 | 32 |
- Use Chebyshev’s theorem to find an interval centered about the mean annual number of strong to violent (F3+) tornados in which you would expect at least 75% of the years to fall.
- Use Chebyshev’s theorem to find an interval centered about the mean annual number of strong to violent (F3+) tornados in which you would expect at least 88.9% of the years to fall.
Solution
a. Variable: \(x =\) number of strong or violent (F3+) tornadoes Chebyshev’s theorem says that at least 75% of the data will fall in the interval from \(\mu-2 \sigma\) to \(\mu+2 \sigma\).
You do not have the population, so you need to estimate the population mean and standard deviation using the sample mean and standard deviation. You can find the sample mean and standard deviation using technology:
\(\overline{x} \approx 46.24, s \approx 22.18\)
So,
\(\mu \approx 46.24, \sigma \approx 22.18\)
\(\mu-2 \sigma \text { to } \mu+2 \sigma\)
\(46.24-2(22.18) \text { to } 46.24+2(22.18)\)
\(46.24-44.36 \text { to } 46.24+44.36\)
\(1.88 \text { to } 90.60\)
Since you can’t have fractional number of tornados, round to the nearest whole number.
At least 75% of the years have between 2 and 91 strong to violent (F3+) tornados. (Actually, all but three years’ values fall in this interval, that means that \(\dfrac{56}{59} \approx 94.9 \%\) actually fall in the interval.)
b. Variable: \(x =\) number of strong or violent (F3+) tornadoes Chebyshev’s theorem says that at least 88.9% of the data will fall in the interval from \(\mu-3 \sigma\) to \(\mu+3 \sigma\).
\(\mu-3 \sigma \text { to } \mu+3 \sigma\)
\(46.24-3(22.18) \text { to } 46.24+3(22.18)\)
\(46.24-66.54 \text { to } 46.24+66.54\)
\(-20.30 \text { to } 112.78\)
Since you can’t have negative number of tornados, the lower limit is actually 0. Since you can’t have fractional number of tornados, round to the nearest whole number.
At least 88.9% of the years have between 0 and 113 strong to violent (F3+) tornados.
(Actually, all but one year falls in this interval, that means that \(\dfrac{58}{59} \approx 98.3 \%\) actually fall in the interval.)
Chebyshev’s Theorem says that at least 75% of the data is within two standard deviations of the mean. That percentage is fairly high. There isn’t much data outside two standard deviations. A rule that can be followed is that if a data value is within two standard deviations, then that value is a common data value. If the data value is outside two standard deviations of the mean, either above or below, then the number is uncommon. It could even be called unusual. An easy calculation that you can do to figure it out is to find the difference between the data point and the mean, and then divide that answer by the standard deviation. As a formula this would be
\(\dfrac{x-\mu}{\sigma}\).
If you don’t know the population mean, \(\mu\), and the population standard deviation, \(\sigma\), then use the sample mean, \(\overline{x}\), and the sample standard deviation, \(s\), to estimate the population parameter values. However, realize that using the sample standard deviation may not actually be very accurate.
Example \(\PageIndex{5}\) determining if a value is unusual
- In 1974, there were 131 strong or violent (F3+) tornados in the United States. Is this value unusual? Why or why not?
- In 1987, there were 15 strong or violent (F3+) tornados in the United States. Is this value unusual? Why or why not?
Solution
a. Variable: \(x =\) number of strong or violent (F3+) tornadoes
To answer this question, first find how many standard deviations 131 is from the mean. From Example \(\PageIndex{4}\), we know \(\mu \approx 46.24\) and \(\sigma \approx 22.18\). For \(x = 131\),
\(\dfrac{x-\mu}{\sigma}=\dfrac{131-46.24}{22.18} \approx 3.82\)
Since this value is more than 2, then it is unusual to have 131 strong or violent (F3+) tornados in a year.
b. Variable: \(x =\) number of strong or violent (F3+) tornadoes For this question the \(x = 15\),
\(\dfrac{x-\mu}{\sigma}=\dfrac{15-46.24}{22.18} \approx-1.41\)
Since this value is between -2 and 2, then it is not unusual to have only 15 strong or violent (F3+) tornados in a year.
Homework
Exercise \(\PageIndex{1}\)
- Cholesterol levels were collected from patients two days after they had a heart attack (Ryan, Joiner & Ryan, Jr, 1985) and are in Example \(\PageIndex{8}\). Find the mean, median, range, variance, and standard deviation using technology.
270 236 210 142 280 272 160 220 226 242 186 266 206 318 294 282 234 224 276 282 360 310 280 278 288 288 244 236 Table \(\PageIndex{8}\): Cholesterol Levels - The lengths (in kilometers) of rivers on the South Island of New Zealand that flow to the Pacific Ocean are listed in Example \(\PageIndex{9}\) (Lee, 1994).
Table \(\PageIndex{9}\): Lengths of Rivers (km) Flowing to Pacific Ocean River Length (km) River Length (km) Clarence 209 Clutha 322 Conway 48 Taieri 288 Waiau 169 Shag 72 Hurunui 138 Kakanui 64 Waipara 64 Waitaki 209 Ashley 97 Waihao 64 Waimakariri 161 Pareora 56 Selwyn 95 Rangitata 121 Rakaia 145 Ophi 80 Ashburton 90 a. Find the mean and median.
b. Find the range.
c. Find the variance and standard deviation. - The lengths (in kilometers) of rivers on the South Island of New Zealand that flow to the Pacific Ocean are listed in Example \(\PageIndex{9}\) (Lee, 1994).
River Length (km) River Length (km) Hollyford 76 Waimea 48 Cascade 64 Motueka 108 Arawhata 68 Takaka 72 Haast 64 Aorere 72 Karangarua 37 Heaphy 35 Cook 32 Karamea 80 Waiho 32 Mokihinui 56 Whataroa 51 Buller 177 Wanganui 56 Grey 121 Waitaha 40 Taramakau 80 Hokitika 64 Arahura 56 Table \(\PageIndex{10}\): Lengths of Rivers (km) Flowing to Tasman Sea
a. Find the mean and median.
b. Find the range.
c. Find the variance and standard deviation. - Eyeglassmatic manufactures eyeglasses for their retailers. They test to see how many defective lenses they made the time period of January 1 to March 31. Example \(\PageIndex{11}\) gives the defect and the number of defects.
Defect type Number of defects Scratch 5865 Right shaped - small 4613 Flaked 1992 Wrong axis 1838 Chamfer wrong 1596 Crazing, cracks 1546 Wrong shape 1485 Wrong PD 1398 Spots and bubbles 1371 Wrong height 1130 Right shape - big 1105 Lost in lab 976 Spots/bubble - intern 976
Table \(\PageIndex{11}\): Number of Defective Lenses
a. Find the mean and median.
b. Find the range.
c. Find the variance and standard deviation. - Print-O-Matic printing company’s employees have salaries that are contained in Example \(\PageIndex{12}\). Find the mean, median, range, variance, and standard deviation using technology.
Employee Salary ($) Employee Salary ($) CEO 272,500 Administration 66,346 Driver 58,456 Sales 109,739 CD74 100,702 Designer 90,090 CD65 57,380 Platens 69,573 Embellisher 73,877 Polar 75,526 Folder 65,270 ITEK 64,553 GTO 74,235 Mgmt 108,448 Pre Press Manager 108,448 Handwork 52,718 Pre Press Manager/IT 98,837 Horizon 76,029 Pre Press/ Graphic Artist 75,311 Table \(\PageIndex{12}\): Salaries of Print-O-Matic Printing Company Employees - Print-O-Matic printing company spends specific amounts on fixed costs every month. The costs of those fixed costs are in Example \(\PageIndex{13}\).
Table \(\PageIndex{13}\): Fixed Costs for Print-O-Matic Printing Company Monthly charges Monthly cost ($) Bank charges 482 Cleaning 2208 Computer expensive 2471 Lease payments 2656 Postage 2117 Uniforms 2600 a. Find the mean and median.
b. Find the range.
c. Find the variance and standard deviation. - Compare the two data sets in problems 2 and 3 using the mean and standard deviation. Discuss which mean is higher and which has a larger spread of the data.
- Example \(\PageIndex{14}\) contains pulse rates collected from males, who are non-smokers but do drink alcohol ("Pulse rates before," 2013). The before pulse rate is before they exercised, and the after pulse rate was taken after the subject ran in place for one minute. Compare the two data sets using the mean and standard deviation. Discuss which mean is higher and which has a larger spread of the data.
Pulse before Pulse after Pulse before Pulse after 76 88 59 92 56 110 60 104 64 126 65 82 50 90 76 150 49 83 145 155 68 136 84 140 68 125 78 141 88 150 85 131 80 146 78 132 78 168 Table \(\PageIndex{14}\): Pulse Rates of Males Before and After Exercise - Example \(\PageIndex{15}\) contains pulse rates collected from females, who are non-smokers but do drink alcohol ("Pulse rates before," 2013). The before pulse rate is before they exercised, and the after pulse rate was taken after the subject ran in place for one minute. Compare the two data sets using the mean and standard deviation. Discuss which mean is higher and which has a larger spread of the data.
Pulse before Pulse after Pulse before Pulse after 96 176 92 120 82 150 70 96 86 150 75 130 72 115 70 119 78 129 70 95 90 160 68 84 88 120 47 136 71 125 64 120 66 89 70 98 76 132 74 168 70 120 85 130 Table \(\PageIndex{15}\): Pulse Rates of Females Before and After Exercise - To determine if Reiki is an effective method for treating pain, a pilot study was carried out where a certified second-degree Reiki therapist provided treatment on volunteers. Pain was measured using a visual analogue scale (VAS) immediately before and after the Reiki treatment (Olson & Hanson, 1997) and the data is in Example \(\PageIndex{16}\). Compare the two data sets using the mean and standard deviation. Discuss which mean is higher and which has a larger spread of the data.
VAS before VAS after VAS before VAS after 6 3 5 1 2 1 1 0 2 0 6 4 9 1 6 1 3 0 4 4 3 2 4 1 4 1 7 6 5 2 2 1 2 2 4 3 3 0 8 8 Table \(\PageIndex{16}\): Pain Measurements Before and After Reiki Treatment - Example \(\PageIndex{17}\) contains data collected on the time it takes in seconds of each passage of play in a game of rugby. ("Time of passages," 2013)
Table \(\PageIndex{17}\): Times (in seconds) of rugby plays 39.2 2.7 9.2 14.6 1.9 17.8 15.5 53.8 17.5 27.5 4.8 8.6 22.1 29.8 10.4 9.8 27.7 32.7 32 34.3 29.1 6.5 2.8 10.8 9.2 12.9 7.1 23.8 7.6 36.4 35.6 28.4 37.2 16.8 21.2 14.7 44.5 24.7 36.2 20.9 19.9 24.4 7.9 2.8 2.7 3.9 14.1 28.4 45.5 38 18.5 8.3 56.2 10.2 5.5 2.5 46.8 23.1 9.2 10.3 10.2 22 28.5 24 17.3 12.7 15.5 4 5.6 3.8 21.6 49.3 52.4 50.1 30.5 37.2 15 38.7 3.1 11 10 5 48.8 3.6 12.6 9.9 58.6 37.9 19.4 29.2 12.3 39.2 22.2 39.7 6.4 2.5 34 a. Using technology, find the mean and standard deviation.
b. Use Chebyshev’s theorem to find an interval centered about the mean times of each passage of play in the game of rugby in which you would expect at least 75% of the times to fall.
c. Use Chebyshev’s theorem to find an interval centered about the mean times of each passage of play in the game of rugby in which you would expect at least 88.9% of the times to fall. - Yearly rainfall amounts (in millimeters) in Sydney, Australia, are in table #3.2.18 ("Annual maximums of," 2013).
Table \(\PageIndex{18}\): Yearly Rainfall Amounts in Sydney, Australia 146.8 383 90.9 178.1 267.5 95.5 156.5 180 90.9 139.7 200.2 171.7 187.2 184.9 70.1 58 84.1 55.6 133.1 271.8 135.9 71.9 99.4 110.6 47.5 97.8 122.7 58.4 154.4 173.7 118.8 88 84.6 171.5 254.3 185.9 137.2 138.9 96.2 85 45.2 74.7 264.9 113.8 133.4 68.1 156.4 a. Using technology, find the mean and standard deviation.
b. Use Chebyshev’s theorem to find an interval centered about the mean yearly rainfall amounts in Sydney, Australia, in which you would expect at least 75% of the amounts to fall.
c. Use Chebyshev’s theorem to find an interval centered about the mean yearly rainfall amounts in Sydney, Australia, in which you would expect at least 88.9% of the amounts to fall. - The number of deaths attributed to UV radiation in African countries in the year 2002 is given in Example \(\PageIndex{19}\) ("UV radiation: Burden," 2013).
Table \(\PageIndex{19}\): Number of Deaths from UV Radiation 50 84 31 338 6 504 40 7 58 204 15 27 39 1 45 174 98 94 199 9 27 58 356 5 45 5 94 26 171 13 57 138 39 3 171 41 1177 102 123 433 35 40 456 125 a. Using technology, find the mean and standard deviation.
b. Use Chebyshev’s theorem to find an interval centered about the mean number of deaths from UV radiation in which you would expect at least 75% of the numbers to fall.
c. Use Chebyshev’s theorem to find an interval centered about the mean number of deaths from UV radiation in which you would expect at least 88.9% of the numbers to fall. - The time (in 1/50 seconds) between successive pulses along a nerve fiber ("Time between nerve," 2013) are given in Example \(\PageIndex{20}\).
Table \(\PageIndex{20}\): Time (in 1/50 seconds) Between Successive Pulses 10.5 1.5 2.5 5.5 29.5 3 9 27.5 18.5 4.5 7 9.5 1 7 4.5 2.5 7.5 11.5 7.5 4 12 8 3 5.5 7.5 4.5 1.5 10.5 1 7 12 14.5 8 3.5 3.5 2 1 7.5 6 13 7.5 16.5 3 25.5 5.5 14 18 7 27.5 14 a. Using technology, find the mean and standard deviation.
b. Use Chebyshev’s theorem to find an interval centered about the mean time between successive pulses along a nerve fiber in which you would expect at least 75% of the times to fall.
c. Use Chebyshev’s theorem to find an interval centered about the mean time between successive pulses along a nerve fiber in which you would expect at least 88.9% of the times to fall. - Suppose a passage of play in a rugby game takes 75.1 seconds. Would it be unusual for this to happen? Use the mean and standard deviation that you calculated in problem 11.
- Suppose Sydney, Australia received 300 mm of rainfall in a year. Would this be unusual? Use the mean and standard deviation that you calculated in problem 12.
- Suppose in a given year there were 2257 deaths attributed to UV radiation in an African country. Is this value unusual? Use the mean and standard deviation that you calculated in problem 13.
- Suppose it only takes 2 (1/50 seconds) for successive pulses along a nerve fiber. Is this value unusual? Use the mean and standard deviation that you calculated in problem 14.
- Answer
-
1. mean = 253.93, median = 268, range = 218, variance = 2276.29, st dev = 47.71
3. a. mean = 67.68 km, median = 64 km, b. range = 145 km, c. variance = 1107.9416 \(\mathrm{km}^{2}\), st dev = 33.29 km
5. mean = $89,370.42, median = $75,311, range = $219,782, variance =2298639399, st dev = $47,944.13
7. See solutions
9. \(\overline{x}_{1} \approx 75.45, s_{1} \approx 11.10, \overline{x}_{2} \approx 125.55, s_{2} \approx 24.72\)
11. a. \(\overline{x} \approx 21.24 \mathrm{sec}, s \approx 14.95 \mathrm{sec}\) b. \((-8.66 \mathrm{sec}, 51.14 \mathrm{sec})\) c. \((-23.61 \mathrm{sec}, 66.09 \mathrm{sec})\)
13. a. \(\overline{x} \approx 130.98, s \approx 205.44\) b. \((-279.90,541.86)\) c. \((-485.34,747.3)\)
15. 3.61
17. 10.35


