13.5: Mann-Whitney U Test
- Page ID
- 34948
The Mann-Whitney U Test is the non-parametric alternative to the independent t-test. The test was expanded on Frank Wilcoxon’s Rank Sum test by Henry Mann and Donald Whitney.

The independent t-test assumes the populations are normally distributed. When these conditions are not met, the Mann-Whitney Test is an alternative method.
If two groups come from the same distribution and were randomly assigned labels, then the two different groups should have values somewhat equally distributed between the two groups. The Mann-Whitney Test looks at all the possible rankings between the data points. For large sample sizes, a normal approximation of the distribution of ranks is used.
Small Sample Size Case \((n \leq 20)\)
Combine the data from both groups and sort from smallest to largest. Make sure to label the data values so you know which group they came from. Rank the data. Sum the ranks separately from each group. Let \(R_{1}\) = sum of ranks for group one and \(R_{2}\) = sum of ranks for group two.
Find the \(U\) statistic for both groups: \(U_{1} = R_{1} - \frac{n_{1} \left(n_{1}+1\right)}{2}, U_{2} = R_{2} - \frac{n_{2} \left(n_{2}+1\right)}{2}\).
The test statistic \(U = \text{Min} \left(U_{1}, U_{2}\right)\) is the smaller of \(U_{1}\) or \(U_{2}\). Critical values are found given in the tables in Figures 13-6 \((\alpha = 0.05)\) and 13-7 \((\alpha = 0.01)\).
| \(n_{2}\) | |||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| \(n_{1}\) | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 2 | - | - | - | - | - | - | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 2 | 2 | 2 | 2 |
| 3 | - | - | - | 0 | 1 | 1 | 2 | 2 | 3 | 3 | 4 | 4 | 5 | 5 | 6 | 6 | 7 | 7 | 8 |
| 4 | - | - | 0 | 1 | 2 | 3 | 4 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 11 | 12 | 13 | 13 |
| 5 | - | 0 | 1 | 2 | 3 | 5 | 6 | 7 | 8 | 9 | 11 | 12 | 13 | 14 | 15 | 17 | 18 | 19 | 20 |
| 6 | - | 1 | 2 | 3 | 5 | 6 | 8 | 10 | 11 | 13 | 14 | 16 | 17 | 19 | 21 | 22 | 24 | 25 | 27 |
| 7 | - | 1 | 3 | 5 | 6 | 8 | 10 | 12 | 14 | 16 | 18 | 20 | 22 | 24 | 26 | 28 | 30 | 32 | 34 |
| 8 | 0 | 2 | 4 | 6 | 8 | 10 | 13 | 15 | 17 | 19 | 22 | 24 | 26 | 29 | 31 | 34 | 36 | 38 | 41 |
| 9 | 0 | 2 | 4 | 7 | 10 | 12 | 15 | 17 | 21 | 23 | 26 | 28 | 31 | 34 | 37 | 39 | 42 | 45 | 48 |
| 10 | 0 | 3 | 5 | 8 | 11 | 14 | 17 | 20 | 23 | 26 | 29 | 33 | 36 | 39 | 42 | 45 | 48 | 52 | 55 |
| 11 | 0 | 3 | 6 | 9 | 13 | 16 | 19 | 23 | 26 | 30 | 33 | 37 | 40 | 44 | 47 | 51 | 55 | 58 | 62 |
| 12 | 1 | 4 | 7 | 11 | 14 | 18 | 22 | 26 | 29 | 33 | 37 | 41 | 45 | 49 | 53 | 57 | 61 | 65 | 69 |
| 13 | 1 | 4 | 8 | 12 | 16 | 20 | 24 | 28 | 33 | 37 | 41 | 45 | 50 | 54 | 59 | 63 | 67 | 72 | 76 |
| 14 | 1 | 5 | 9 | 13 | 17 | 22 | 26 | 31 | 36 | 40 | 45 | 50 | 55 | 59 | 64 | 67 | 74 | 78 | 83 |
| 15 | 1 | 5 | 10 | 14 | 19 | 24 | 29 | 34 | 39 | 44 | 49 | 54 | 59 | 64 | 70 | 75 | 80 | 85 | 90 |
| 16 | 1 | 6 | 11 | 15 | 21 | 26 | 31 | 37 | 42 | 47 | 53 | 59 | 64 | 70 | 75 | 81 | 86 | 92 | 98 |
| 17 | 2 | 6 | 11 | 17 | 22 | 28 | 34 | 39 | 45 | 51 | 57 | 63 | 67 | 75 | 81 | 87 | 93 | 99 | 105 |
| 18 | 2 | 7 | 12 | 18 | 24 | 30 | 36 | 42 | 48 | 55 | 61 | 67 | 74 | 80 | 86 | 93 | 99 | 106 | 112 |
| 19 | 2 | 7 | 13 | 19 | 25 | 32 | 38 | 45 | 52 | 58 | 65 | 72 | 78 | 85 | 92 | 99 | 106 | 113 | 119 |
| 20 | 2 | 8 | 14 | 20 | 27 | 34 | 41 | 48 | 55 | 62 | 69 | 76 | 83 | 90 | 98 | 105 | 112 | 119 | 127 |
| \(n_{2}\) | |||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| \(n_{1}\) | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 2 | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | 0 | 0 |
| 3 | - | - | - | - | - | - | - | 0 | 0 | 0 | 1 | 1 | 1 | 2 | 2 | 2 | 2 | 3 | 3 |
| 4 | - | - | - | - | 0 | 0 | 1 | 1 | 2 | 2 | 3 | 3 | 4 | 5 | 5 | 6 | 6 | 7 | 8 |
| 5 | - | - | - | 0 | 1 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 7 | 8 | 9 | 10 | 11 | 12 | 13 |
| 6 | - | - | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 9 | 10 | 11 | 12 | 13 | 15 | 16 | 17 | 18 |
| 7 | - | - | 0 | 1 | 3 | 4 | 6 | 7 | 9 | 10 | 12 | 13 | 15 | 16 | 18 | 19 | 21 | 22 | 24 |
| 8 | - | - | 1 | 2 | 4 | 6 | 7 | 9 | 11 | 13 | 15 | 17 | 18 | 20 | 22 | 24 | 26 | 28 | 30 |
| 9 | - | 0 | 1 | 3 | 5 | 7 | 9 | 11 | 13 | 16 | 18 | 20 | 22 | 24 | 27 | 29 | 31 | 33 | 36 |
| 10 | - | 0 | 2 | 4 | 6 | 9 | 11 | 13 | 16 | 18 | 21 | 24 | 26 | 29 | 31 | 34 | 37 | 39 | 42 |
| 11 | - | 0 | 2 | 5 | 7 | 10 | 13 | 16 | 18 | 21 | 24 | 27 | 30 | 33 | 36 | 39 | 42 | 45 | 46 |
| 12 | - | 1 | 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 | 27 | 31 | 34 | 37 | 41 | 44 | 47 | 51 | 54 |
| 13 | - | 1 | 3 | 7 | 10 | 13 | 17 | 20 | 24 | 27 | 31 | 34 | 38 | 42 | 45 | 49 | 53 | 56 | 60 |
| 14 | - | 1 | 4 | 7 | 11 | 15 | 18 | 22 | 26 | 30 | 34 | 38 | 42 | 46 | 50 | 54 | 58 | 63 | 67 |
| 15 | - | 2 | 5 | 8 | 12 | 16 | 20 | 24 | 29 | 33 | 37 | 42 | 46 | 51 | 55 | 60 | 64 | 69 | 73 |
| 16 | - | 2 | 5 | 9 | 13 | 18 | 22 | 27 | 31 | 36 | 41 | 45 | 50 | 55 | 60 | 65 | 70 | 74 | 79 |
| 17 | - | 2 | 6 | 10 | 15 | 19 | 24 | 29 | 34 | 39 | 44 | 49 | 54 | 60 | 65 | 70 | 75 | 81 | 86 |
| 18 | - | 2 | 6 | 11 | 16 | 21 | 26 | 31 | 37 | 42 | 47 | 53 | 58 | 64 | 70 | 75 | 81 | 87 | 92 |
| 19 | 0 | 3 | 7 | 12 | 17 | 22 | 28 | 33 | 39 | 45 | 51 | 56 | 63 | 69 | 74 | 81 | 87 | 93 | 99 |
| 20 | 0 | 3 | 8 | 13 | 18 | 24 | 30 | 36 | 42 | 46 | 54 | 60 | 67 | 73 | 79 | 86 | 92 | 99 | 105 |
If \(U\) is less than or equal to the critical value, then reject \(H_{0}\). Dashes indicate that the sample is too small to reject \(H_{0}\).
If you have only sample size above 20, use the following online calculator to find the critical value: https://www.socscistatistics.com/tests/mannwhitney/default.aspx.
Student employees are a major part of most college campus employment. Two major departments that participate in student hiring are listed below with the number of hours worked by students for a month. At the 0.05 level of significance, is there sufficient evidence to conclude a difference in hours between the two departments?
| Student | Department | Hours | Rank |
|---|---|---|---|
| 1 | Athletics | 12 | 1 |
| 2 | Athletics | 15 | 2 |
| 3 | Athletics | 17 | 3 |
| 4 | Athletics | 18 | 4.5 |
| 5 | Library | 18 | 4.5 |
| 6 | Athletics | 19 | 6.5 |
| 7 | Library | 19 | 6.5 |
| 8 | Athletics | 20 | 8.5 |
| 9 | Library | 20 | 8.5 |
| 10 | Library | 21 | 10 |
| 11 | Athletics | 22 | 11.5 |
| 12 | Library | 22 | 11.5 |
| 13 | Athletics | 24 | 13.5 |
| 14 | Library | 24 | 13.5 |
| 15 | Athletics | 25 | 15.5 |
| 16 | Library | 25 | 15.5 |
| 17 | Library | 26 | 17 |
| 18 | Library | 28 | 18 |
| 19 | Athletics | 30 | 19 |
| 20 | Library | 31 | 20 |
| 21 | Library | 35 | 21 |
Sum the ranks for each group:
\(R_{1} = 1 + 2 + 3 + 4.5 + 6.5 + 8.5 + 11.5 + 13.5 + 15.5 + 19 = 85\)
\(R_{2} = 4.5 + 6.5 +8.5 + 10 + 11.5 + 13.5 + 15.5 + 17 + 18 + 20 + 21 = 146\)
Compute the test statistic:
\(U_{1} = R_{1} - \frac{n_{1} \left(n_{1}+1\right)}{2} = 85 - \frac{10 \cdot 11}{2} = 30\)
\(U_{2} = R_{2} - \frac{n_{2} \left(n_{2}+1\right)}{2} = 146 - \frac{11 \cdot 12}{2} = 80\)
\(U = 30\)
Find the critical value using Figure 13-8, where \(n_{1} = 10\) and \(n_{2} = 11\). The critical value = 26.
Do not reject \(H_{0}\), since \(U = 30 > \text{CV} = 26\).
There is not enough evidence to support the claim that there is a difference in the number of hours student employees work for the athletics department and the library.
Large Sample Size Case (\(n_{1} > 20\) and \(n_{2} > 20\))
Find the \(U\) statistic for both groups: \(U_{1} = R_{1} - \frac{n_{1} \left(n_{1}+1\right)}{2}\), \(U_{2} = R_{2} - \frac{n_{2} \left(n_{2}+1\right)}{2}\).
Let \(U = \text{Min} \left(U_{1}, U_{2}\right)\), the smaller of \(U_{1}\) or \(U_{2}\). The formula for the test statistic is: \[z = \frac{\left(U - \left( \dfrac{n_{1} \cdot n_{2}}{2} \right)\right)}{\sqrt{\dfrac{n_{1} \cdot n_{2} \left(n_{1} + n_{2} + 1\right)}{12}}} \nonumber\]
A manager believes that the sales of coffee at their Portland store is more than the sales at their Cannon Beach store. They take a random sample of weekly sales from the two stores over the last year. Use the Mann-Whitney test to see if the manager’s claim could be true. Use the p-value method with \(\alpha = 0.05\).
| Order | Store | Sales | Rank | Order | Store | Sales | Rank | |
|---|---|---|---|---|---|---|---|---|
| 1 | Portland | 1257 | 1 | 22 | Cannon Beach | 3585 | 21 | |
| 2 | Portland | 1510 | 4.5 | 23 | Cannon Beach | 3853 | 23 | |
| 3 | Portland | 1510 | 4.5 | 24 | Portland | 4025 | 24 | |
| 4 | Cannon Beach | 1510 | 4.5 | 25 | Portland | 4125 | 26.5 | |
| 5 | Cannon Beach | 1510 | 4.5 | 26 | Portland | 4125 | 26.5 | |
| 6 | Cannon Beach | 1510 | 4.5 | 27 | Cannon Beach | 4125 | 26.5 | |
| 7 | Cannon Beach | 1510 | 4.5 | 28 | Cannon Beach | 4125 | 26.5 | |
| 8 | Portland | 1764 | 8.5 | 29 | Cannon Beach | 4399 | 30 | |
| 9 | Cannon Beach | 1764 | 8.5 | 30 | Cannon Beach | 4399 | 30 | |
| 10 | Cannon Beach | 2275 | 10.5 | 31 | Cannon Beach | 4399 | 30 | |
| 11 | Cannon Beach | 2275 | 10.5 | 32 | Portland | 4677 | 32 | |
| 12 | Cannon Beach | 2533 | 12.5 | 33 | Portland | 5244 | 35.5 | |
| 13 | Cannon Beach | 2533 | 12.5 | 34 | Portland | 5244 | 35.5 | |
| 14 | Portland | 3015 | 14 | 35 | Cannon Beach | 5244 | 35.5 | |
| 15 | Portland | 3055 | 15.5 | 36 | Cannon Beach | 5244 | 35.5 | |
| 16 | Portland | 3055 | 15.5 | 37 | Cannon Beach | 5244 | 35.5 | |
| 17 | Portland | 3319 | 18 | 38 | Cannon Beach | 5244 | 35.5 | |
| 18 | Portland | 3319 | 18 | 39 | Portland | 6128 | 39.5 | |
| 19 | Portland | 3319 | 18 | 40 | Portland | 6128 | 39.5 | |
| 20 | Cannon Beach | 3585 | 21 | 41 | Portland | 6134 | 41 | |
| 21 | Cannon Beach | 3585 | 21 | 42 | Portland | 6433 | 42 |
The hypotheses are:
\(H_{0}\): There is no difference in the coffee sales between the Portland and Cannon Beach stores.
\(H_{1}\): There is a difference in the coffee sales between the Portland and Cannon Beach stores.
Sum the ranks for each group.
The sum for the Portland store’s ranks: \(R_{1} = 459.5\).
The sum for the Cannon Beach store’s ranks: \(R_{2} = 443.5\).
Compute the test statistic:
\(U_{1} = R_{1} - \frac{n_{1} \left(n_{1}+1\right)}{2} = 459.5 - \frac{20 \cdot 21}{2} = 249.5\)
\(U_{2} = R_{2} - \frac{n_{2} \left(n_{2}+1\right)}{2} = 443.5 - \frac{22 \cdot 23}{2} = 190.5\)
\(U = 190.5\)
\(z = \frac{190.5 - \left(\frac{20 \cdot 22}{2}\right)}{\sqrt{ \left(\frac{20 \cdot 22 (20 + 22 + 1)}{12}\right) }} = -0.7429\)
This test uses the standard normal distribution with the same technique for finding a p-value or critical value as the z-test performed in previous chapters. Compute the p-value for a standard normal distribution for \(z = -0.7429\) for a two-tailed test using \(2 * \text{normalcdf}(-1E99,-0.7429,0,1) = 0.4575\).
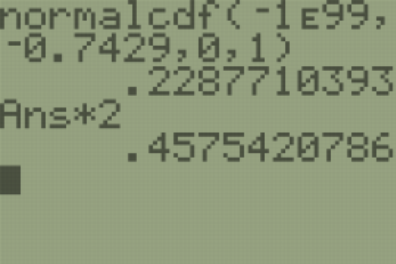.png?revision=1)
The p-value = \(0.4575 > \alpha = 0.05\); therefore, do not reject \(H_{0}\).
This is a two-tailed test with \(\alpha = 0.05\). Use the lower tail area of \(\alpha/2 = 0.05\) and you get critical values of \(z_{\alpha/2} = \pm 1.96\).
There is not enough evidence to support the claim that there is a difference in coffee sales between the Portland and Cannon beach stores.
There are no shortcut keys on the TI calculators or Excel for this Nonparametric Test. Note that if your data has tied ranks, there are several methods not addressed in this text, to correct the standard deviation. Hence, the z-score in some software packages may not match your results calculated by hand.


