5.5: Hypergeometric Distribution
- Page ID
- 26587
The hypergeometric distribution is a discrete probability distribution used to find the probability of success when there are two outcomes to each trial, and there are a set number of dependent trials. A hypergeometric probability distribution results from a random experiment that meets all of the following requirements. 12
- The procedure has a fixed sample size n taken from a population N.
- The trials are taken without replacement (dependent).
- Each trial has exactly two outcomes, the number of successes = a and the number of failures = b. Note a + b = N.
If a random experiment satisfies all of the above, the distribution of the random variable X, where X counts the number of successes, is called a hypergeometric distribution, we write X ~ H(n, a, N).
The hypergeometric distribution is P(X = x) = \(\frac{ {}_{a} C_{x} \cdot {}_{b} C_{n-x}}{ {}_{N} C_{n}}\), x = 0, 1, 2, … , n or a, whichever is smaller. Where n is the sample size taken without replacement from the population size N, x is the number of successes out of n that you are trying to find the probability for, a is the number of a successes and b = N – a is the number of failures out of the population N.
A committee of 5 people is to be formed from 15 volunteers and 6 appointed positions. Compute the probability that the committee will consist of 4 randomly selected volunteers.
Solution
There are a total of N = 15 + 6 = 21 people. A sample of n = 5 people are selected without replacement. The success is choosing a volunteer, so a = 15. Of the 15 volunteers, we are asked to find the probability of selecting x = 4. Substitute in each value: P(X = 4) = \(\frac{ {}_{15} C_{4} \cdot { }_{6} C_{1}}{ {}_{21} C_{5}} = 0.4025\).
There is a pattern to the numbers in the formula. The top two numbers on the left of the C’s add up to the bottom number on the left of C, and the top two numbers on the right of the C’s add up to the bottom number on the right of C.
The waiting room for jury selection has 40 people with a college degree and 30 people without. A jury of 12 is selected from this waiting room. What is the probability that exactly 5 of the jury members will have a college degree?
Solution
There are a total of N = 40 + 30 = 70 people. A sample of n = 12 people are selected without replacement. The success is choosing someone with a college degree, so a = 40. Of the 12 jurors we are asked to find the probability of selecting x = 5.
Substitute in each value: P(X = 5) = \(\frac{ {}_{40} C_{5} \cdot { }_{30} C_{7}}{ {}_{70} C_{12}} = 0.1259\).
A wallet contains three $100 bills and five $1 bills. You randomly choose four bills. What is the probability that you will choose exactly two $100 bills?
Solution
There are a total of N = 3 + 5 = 8 bills. A sample of n = 4 bills are selected without replacement. The success is choosing a $100 bill, so a = 3. Of the 3 $100 bills we are asked to find the probability of selecting x = 2. Substitute in each value: P(X = 2) = \(\frac{ {}_{3} C_{2} \cdot { }_{5} C_{2}}{ {}_{8} C_{4}} = 0.4286\).
Note: the calculator does not have the hypergeometric distribution shortcut. The following online calculator will calculate the probability: https://homepage.divms.uiowa.edu/~mbognar/applets/hg.html. The M = a is the number of successes a from our example, or use Excel.
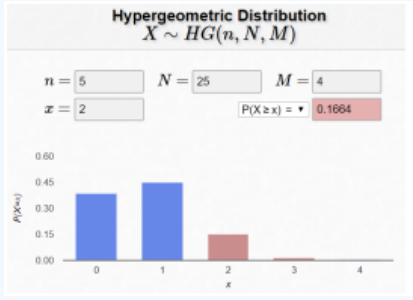
Figure 5-7 may help you decide when to use the “True” for cumulative in Excel. Figure 5-7 A bookstore owner examines 5 books from each lot of 25 to check for missing pages. If they find at least 2 books with missing pages, the entire lot is returned. If, indeed, there are 4 books with missing pages, find the probability that the lot will be returned. Sometimes the hardest part is determining which of the numbers goes in the right place in the formula. The population size is always the largest number, N = 25. A success is what you are trying to find the probability for, which is getting a book with a missing page. The number of successes out of the population is a = 4 (the 4 books with the missing pages). This means b = 25 – 4 = 21 (the number of books without missing pages). Note a + b = N. The sample size is the n = 5 is the number of books the owner examines. The owner will send the lot back if X is at least 2 missing pages. We can stop at X = 4 since there are only 4 books with missing pages. Your stopping point will be the smaller of n or a. P(X ≥ 2) = P(X = 2) + P(X = 3) + P(X = 4) = \(\frac{ {}_{4} C_{2} \cdot {}_{21} C_{3}}{ {}_{25} C_{5}} + \frac{ {}_{4} C_{3} \cdot {}_{21} C_{2}}{ {}_{25} C_{5}} + \frac{ {}_{4} C_{4} \cdot {}_{21} C_{1}}{ {}_{25} C_{5}} = 0.1502 + 0.0158 + 0.0004 = 0.1664\). In Excel use the formula: =1- HYPGEOM.DIST(1,5,4,25,TRUE). Figure 5-8 shows the online calculator at https://homepage.divms.uiowa.edu/~mbognar/applets/hg.html.
Figure 5-8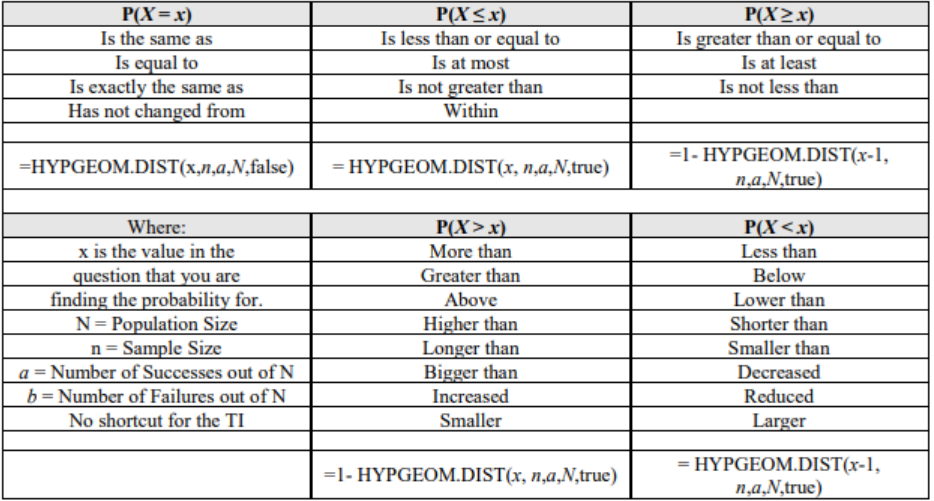
Solution