12.E: Tests of Means (Exercises)
- Page ID
- 2347
General Questions
Q1
The scores of a random sample of \(8\) students on a physics test are as follows: \(60, 62, 67, 69, 70, 72, 75, 78\).
- Test to see if the sample mean is significantly different from \(65\) at the \(0.05\) level. Report the \(t\) and \(p\) values.
- The researcher realizes that she accidentally recorded the score that should have been \(76\) as \(67\). Are these corrected scores significantly different from \(65\) at the \(0.05\) level? (relevant section)
Q2
A (hypothetical) experiment is conducted on the effect of alcohol on perceptual motor ability. Ten subjects are each tested twice, once after having two drinks and once after having two glasses of water. The two tests were on two different days to give the alcohol a chance to wear off. Half of the subjects were given alcohol first and half were given water first. The scores of the \(10\) subjects are shown below. The first number for each subject is their performance in the "water" condition. Higher scores reflect better performance. Test to see if alcohol had a significant effect. Report the \(t\) and \(p\) values. (relevant section)
|
water |
alcohol |
|
16 |
13 |
|
15 |
13 |
|
11 |
10 |
|
20 |
18 |
|
19 |
17 |
|
14 |
11 |
|
13 |
10 |
|
15 |
15 |
|
14 |
11 |
|
16 |
16 |
Q3
The scores on a (hypothetical) vocabulary test of a group of \(20\) year olds and a group of \(60\) year olds are shown below.
|
20 yr olds |
60 yr olds |
|
27 |
26 |
|
26 |
29 |
|
21 |
29 |
|
24 |
29 |
|
15 |
27 |
|
18 |
16 |
|
17 |
20 |
|
12 |
27 |
|
13 |
- Test the mean difference for significance using the \(0.05\) level. (relevant section).
- List the assumptions made in computing your answer.(relevant section)
Q4
The sampling distribution of a statistic is normally distributed with an estimated standard error of \(12\), (\(df = 20)\).
- What is the probability that you would have gotten a mean of \(107\) (or more extreme) if the population parameter were \(100\)? Is this probability significant at the \(0.05\) level (two-tailed)?
- What is the probability that you would have gotten a mean of \(95\) or less (one-tailed)? Is this probability significant at the \(0.05\) level? You may want to use the t Distribution calculator for this problem. (relevant section)
Q5
How do you decide whether to use an independent groups \(t\) test or a correlated \(t\) test (test of dependent means)? (relevant section & relevant section)
Q6
An experiment compared the ability of three groups of subjects to remember briefly-presented chess positions. The data are shown below.
|
Non-players |
Beginners |
Tournament players |
|
22.1 |
32.5 |
40.1 |
|
22.3 |
37.1 |
45.6 |
|
26.2 |
39.1 |
51.2 |
|
29.6 |
40.5 |
56.4 |
|
31.7 |
45.5 |
58.1 |
|
33.5 |
51.3 |
71.1 |
|
38.9 |
52.6 |
74.9 |
|
39.7 |
55.7 |
75.9 |
|
43.2 |
55.9 |
80.3 |
|
43.2 |
57.7 |
85.3 |
- Using the Tukey HSD procedure, determine which groups are significantly different from each other at the \(0.05\) level. (relevant section)
- Now compare each pair of groups using \(t\)-tests. Make sure to control for the familywise error rate (at \(0.05\)) by using the Bonferroni correction. Specify the alpha level you used.
Q7
Below are data showing the results of six subjects on a memory test. The three scores per subject are their scores on three trials (\(a\), \(b\), and \(c\)) of a memory task. Are the subjects getting better each trial? Test the linear effect of trial for the data.
|
a |
b |
c |
|
4 |
6 |
7 |
|
3 |
7 |
8 |
|
2 |
8 |
5 |
|
1 |
4 |
7 |
|
4 |
6 |
9 |
|
2 |
4 |
2 |
- Compute \(L\) for each subject using the contrast weights \(-1\), \(0\), and \(1\). That is, compute \((-1)(a) + (0)(b) + (1)(c)\) for each subject.
- Compute a one-sample \(t\)-test on this column (with the \(L\) values for each subject) you created. (relevant section)
Q8
Participants threw darts at a target. In one condition, they used their preferred hand; in the other condition, they used their other hand. All subjects performed in both conditions (the order of conditions was counterbalanced). Their scores are shown below.
|
Preferred |
Non-preferred |
|
12 |
7 |
|
7 |
9 |
|
11 |
8 |
|
13 |
10 |
|
10 |
9 |
- Which kind of \(t\)-test should be used?
- Calculate the two-tailed \(t\) and \(p\) values using this \(t\) test.
- Calculate the one-tailed \(t\) and \(p\) values using this \(t\) test.
Q9
Assume the data in the previous problem were collected using two different groups of subjects: One group used their preferred hand and the other group used their non-preferred hand. Analyze the data and compare the results to those for the previous problem (relevant section)
Q10
You have \(4\) means, and you want to compare each mean to every other mean.
- How many tests total are you going to compute?
- What would be the chance of making at least one Type I error if the Type I error for each test was \(0.05\) and the tests were independent? (relevant section & relevant section)
- Are the tests independent and how does independence/non-independence affect the probability in (b).
Q11
In an experiment, participants were divided into \(4\) groups. There were \(20\) participants in each group, so the degrees of freedom (error) for this study was \(80 - 4 = 76\). Tukey's HSD test was performed on the data.
- Calculate the \(p\) value for each pair based on the \(Q\) value given below. You will want to use the Studentized Range Calculator.
- Which differences are significant at the \(0.05\) level? (relevant section)
|
Comparison of Groups |
Q |
|
A - B |
3.4 |
|
A - C |
3.8 |
|
A - D |
4.3 |
|
B - C |
1.7 |
|
B - D |
3.9 |
|
C - D |
3.7 |
Q12
If you have \(5\) groups in your study, why shouldn't you just compute a \(t\) test of each group mean with each other group mean? (relevant section)
Q13
You are conducting a study to see if students do better when they study all at once or in intervals. One group of \(12\) participants took a test after studying for one hour continuously. The other group of \(12\) participants took a test after studying for three twenty minute sessions. The first group had a mean score of \(75\) and a variance of \(120\). The second group had a mean score of \(86\) and a variance of \(100\).
- What is the calculated \(t\) value? Are the mean test scores of these two groups significantly different at the \(0.05\) level?
- What would the \(t\) value be if there were only \(6\) participants in each group? Would the scores be significant at the \(0.05\) level?
Q14
A new test was designed to have a mean of \(80\) and a standard deviation of \(10\). A random sample of \(20\) students at your school take the test, and the mean score turns out to be \(85\). Does this score differ significantly from \(80\)? To answer this problem, you may want to use the Normal Distribution Calculator.(relevant section)
Q15
You perform a one-sample \(t\) test and calculate a \(t\) statistic of \(3.0\). The mean of your sample was \(1.3\) and the standard deviation was \(2.6\). How many participants were used in this study? (relevant section)
Q16
True/false: The contrasts \((-3, 1 1 1)\) and \((0, 0 , -1, 1)\) are orthogonal. (relevant section)
Q17
True/false: If you are making \(4\) comparisons between means, then based on the Bonferroni correction, you should use an alpha level of \(0.01\) for each test. (relevant section)
Q18
True/false: Correlated \(t\) tests almost always have greater power than independent \(t\) tests. (relevant section)
Q19
True/false:The graph below represents a violation of the homogeneity of variance assumption. (relevant section)
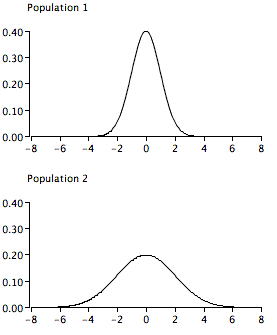
Q20
True/false: When you are conducting a one-sample \(t\) test and you know the population standard deviation, you look up the critical \(t\) value in the table based on the degrees of freedom. (relevant section)
Questions from Case Studies
The following questions use data from the Angry Moods (AM) case study.
Q21
(AM#17) Do athletes or non-athletes calm down more when angry? Conduct a \(t\) test to see if the difference between groups in Control-In scores is statistically significant.
Q22
Do people in general have a higher Anger-Out or Anger-In score? Conduct a \(t\) test on the difference between means of these two scores. Are these two means independent or dependent? (relevant section)
The following questions use data from the Smiles and Leniency (SL) case study.
Q23
Compare each mean to the neutral mean. Be sure to control for the familywise error rate. (relevant section)
Q24
Does a "felt smile" lead to more leniency than other types of smiles?
- Calculate \(L\) (the linear combination) using the following contrast weights \(false: -1,\; felt: 2,\; miserable: -1,\; neutral: 0\).
- Perform a significance test on this value of \(L\). (relevant section)
The following questions are from the Animal Research (AR) case study.
Q25
(AR#8) Conduct an independent samples \(t\) test comparing males to females on the belief that animal research is necessary. (relevant section)
Q26
(AR#9) Based on the \(t\) test you conducted in the previous problem, are you able to reject the null hypothesis if \(alpha = 0.05\)? What about if \(alpha = 0.1\)? (relevant section)
Q27
(AR#10) Is there any evidence that the \(t\) test assumption of homogeneity of variance is violated in the \(t\) test you computed in #25? (relevant section)
The following questions use data from the ADHD Treatment (AT) case study.
Q28
Compare each dosage with the dosage below it (compare \(d0\) and \(d15\), \(d15\) and \(d30\), and \(d30\) and \(d60\)). Remember that the patients completed the task after every dosage.
- If the familywise error rate is \(0.05\), what is the alpha level you will use for each comparison when doing the Bonferroni correction?
- Which differences are significant at this level? (relevant section)
Q29
Does performance increase linearly with dosage?
- Plot a line graph of this data.
- Compute \(L\) for each patient. To do this, create a new variable where you multiply the following coefficients by their corresponding dosages and then sum up the total: \((-3)d0 + (-1)d15 + (1)d30 + (3)d60\) (see #8). What is the mean of \(L\)?
- Perform a significance test on \(L\). Compute the \(95\%\) confidence interval for \(L\). (relevant section)
Select Answers
S1
- \(t(7) = 1.91\)
S4
- \(0.035\)
S7
- two-tailed \(p = 0.0088\)
S8
- \(p = 0.1662\)
S11
- \(A - B: p = 0.085\)
S13
- \(t(22) = 2.57\)
S23
\(t(76) = 3.04\)
S25
- \(p = 0.0745\)
S29
- \(p = 0.0006\)


