Skip to main content
Statistics LibreTexts

15.2.6: Chapter 7 Homework

  1. Last updated
  2. Save as PDF
  • Page ID
    28309

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

    \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

    \( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

    ( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

    \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

    \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

    \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

    \( \newcommand{\Span}{\mathrm{span}}\)

    \( \newcommand{\id}{\mathrm{id}}\)

    \( \newcommand{\Span}{\mathrm{span}}\)

    \( \newcommand{\kernel}{\mathrm{null}\,}\)

    \( \newcommand{\range}{\mathrm{range}\,}\)

    \( \newcommand{\RealPart}{\mathrm{Re}}\)

    \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

    \( \newcommand{\Argument}{\mathrm{Arg}}\)

    \( \newcommand{\norm}[1]{\| #1 \|}\)

    \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

    \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    \( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

    \( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

    \( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

    \( \newcommand{\vectorC}[1]{\textbf{#1}} \)

    \( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

    \( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

    \( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

    \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

    \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

    \(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)
    1. The completion time (in minutes) for a student to complete a short quiz follows the probability density function shown here, with some areas calculated.

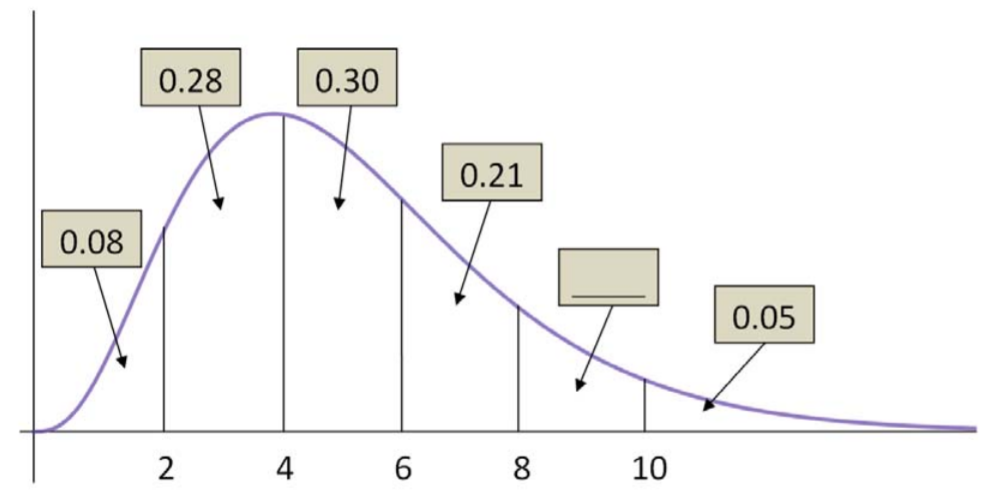
    clipboard_ebf3b119b615d74d05da53f328901dd32.png

    1. Find the probability that a student completes the exam in 4 minutes or less.
    2. Find the probability that a student needs between 8 and 10 minutes to finish the quiz.
    3. If the instructor allows 10 minutes for the quiz and the class has 40 students, how many students will run out of time before the quiz is finished?
    4. Find the 64th percentile of the distribution.
    1. A ferry boat leaves the dock once per hour. Your waiting time for the next ferry boat will follow a uniform distribution from 0 to 60 minutes.
      1. Find the mean and variance of this random variable.
      2. Find the probability of waiting more than 20 minutes for the next  ferry.
      3. Find the probability of waiting exactly 20 minutes for the next ferry.
      4. Find the probability of waiting between 15 and 35 minutes for the next ferry.
      5. Find the conditional probability of waiting at least 10 more minutes after you have already waited 15 minutes.
      6. Find the probability of waiting more than 45 minutes for the ferry on 3 consecutive independent days.
    2. The cycle times for a truck hauling concrete to a highway construction site are uniformly distributed over the interval 50 to 70 minutes.  
      1. Find the mean and variance for cycle times.
      2. Find the 5th and 95th percentile of cycle times.
      3. Find the interquartile range.
      4. Find the probability that the cycle time for a randomly selected truck exceeds 62 minutes.
      5. If you are given that the cycle time exceeds 55 minutes, find the probability that the cycle time is between 60 and 65 minutes.
    3. The amount of gas in a car’s tank (X) follows a Uniform Distribution, in which the minimum is zero and the maximum is 12 gallons.
      1. Find the mean and median amount of gas in the tank.
      2. Find the variance and standard deviation of gas in the tank.
      3. Find the probability that there is more than 3 gallons in the tank.
      4. Find the probability that there is between 4 and 6 gallons in the tank.
      5. Find the probability that there is exactly 3 gallons in the tank.
      6. Find the 80th percentile of gas in the tank.
    4. A normally distributed population of package weights has a mean of 63.5 g and a standard deviation of 12.2 g.
      1. What percentage of this population weighs 66 g or more?  
      2. What percentage of this population weighs 41 g or less?
      3. What percentage of this population weighs between 41 g and 66 g?
      4. Find the 60th percentile for distribution of weights.
      5. Find the three quartiles and the interquartile range.
    5. Assume the expected waiting time until the next RM (Richter Magnitude) 7.0 or greater earthquake somewhere in California follows an exponential distribution with \(\mu=10\) years.
      1. Find the probability of waiting 10 or more years for the next  RM 7.0 or greater earthquake.
      2. Determine the median waiting time until the next RM 7.0 or greater earthquake.
    6. High Fructose Corn Syrup (HFCS)  is a sweetener in food products that is linked to obesity and Type 2 Diabetes. The mean annual consumption in the United States in 2008 of HFCS was 60 lbs with a standard deviation of 20 lbs. Assume the population follows a Normal Distribution.
      1. Find the probability that a randomly selected American consumes more than 50 lbs of HFCS per year.
      2. Find the probability that a randomly selected American consumes between 30 and 90 lbs of HFCS per year.
      3. Find the 80th percentile of annual consumption of HFCS.
      4. Between what two numbers would you expect to contain 95% of Americans HFCS annual consumption?
      5. Find the quartiles and Interquartile range for this population.
      6. A teenager who loves soda consumes 105 lbs of HFCS per year. Is this result unusual? Use probability to justify your answer.
    7. A nuclear power plant experiences serious accidents once every 8 years. Let X = the waiting time until the next serious accident.
      1. What is the mean and standard deviation of the random variable X?
      2. Determine the probability of waiting more than 10 years before the next serious accident.
      3. Suppose a plant went  5 years without a serious accident. Find the probability of waiting more than 10 years before the next serious accident.
      4. Determine the probability of waiting less than 5 years before the next serious accident.
      5. What is median waiting time until the next serious accident?
      6. Find the Interquartile range for this distribution.

     

    This page titled 15.2.6: Chapter 7 Homework is shared under a CC BY-SA 4.0 license and was authored, remixed, and/or curated by Maurice A. Geraghty via source content that was edited to the style and standards of the LibreTexts platform.