7.3: Uniform Distribution

A uniform distribution is a continuous random variable in which all values between a minimum value and a maximum value have the same probability.  

The two parameters that define the Uniform Distribution are:

\(a\)= minimum         \(b\) = maximum

The probability density function is the constant function \(f(x) = 1/(b‐a)\), which creates a rectangular shape.  

Example: Loose leaf tea

A tea lover enjoys Tie Guan Yin loose leaf tea and drinks it frequently. To save money, when the supply gets to 50 grams he will purchase this popular Chinese tea in a 1000 gram package.  

The amount of tea currently in stock follows a uniform random variable.

Solution

\(X\) = the amount of tea currently in stock

\(a\) = minimum = 50 grams   

\(b\) = maximum = 1050 grams

\(f(x) = 1/(1050 ‐ 50) = 0.001\)

The expected value, population variance and standard deviation are calculated using the formulas:

\[\mu=\dfrac{a+b}{2} \qquad \sigma^{2}=\dfrac{(b-a)^{2}}{12} \qquad \sigma=\sqrt{\dfrac{(b-a)^{2}}{12}} \nonumber \]

For the loose leaf tea problem:

\(\mu=\dfrac{50+1050}{2}=550\)g

\(\sigma^{2}=\dfrac{(1050-50)^{2}}{12}=83,333\)

\(\sigma=\sqrt{83333}=289\)g

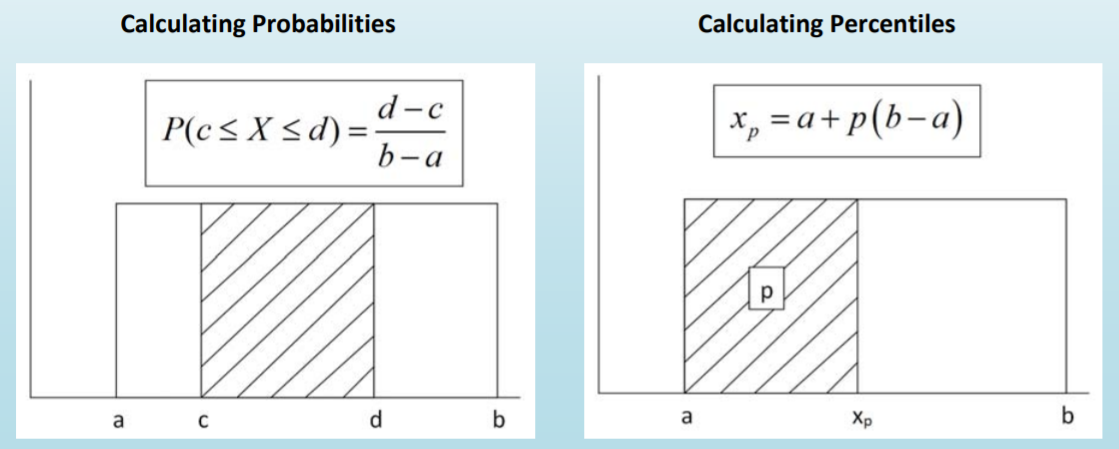
Probability problems can be easily solved by finding the area of rectangles.  

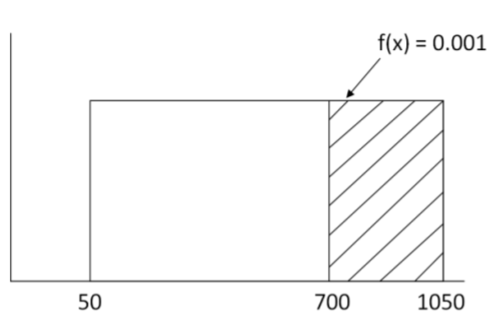
Find the probability that there are at least 700 grams of Tie Guan Yin tea in stock.

\(P(X \geq 700)=\text { width } \times \text { height }=(1050-700)(0.001)=0.35\)

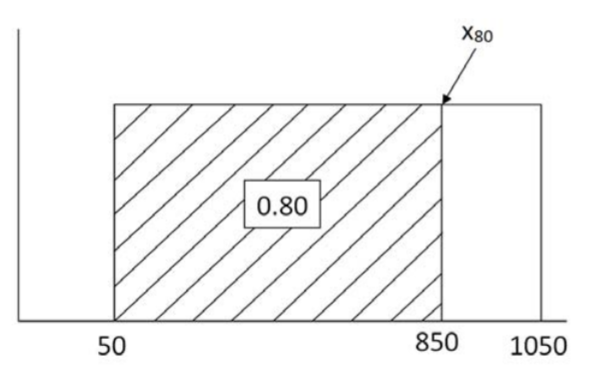
The \(p^{th}\) percentile of the Uniform Distribution is calculated by using linear interpolation: \(x_{p}=a+p(b-a)\)

Find the \(80^{th}\) percentile of Tie Guan Yin in stock:

\(x_{80}=50+0.80(1050-50)=850\) grams

The important features of the Uniform Distribution are summarized here:

Uniform Probability Distribution (parameters: \(a, b\))

\(a\) = minimum value

\(b\) = maximum value

\(a \leq X \leq b\): All values of \(X\) between \(a\) and \(b\) are equally likely

\(f(x)=\dfrac{1}{b-a}\)

\(\mu=\dfrac{a+b}{2}\)

\(\sigma^{2}=\dfrac{(b-a)^{2}}{12}\)

\(\sigma=\sqrt{\dfrac{(b-a)^{2}}{12}}\)

Example: Waiting for a train

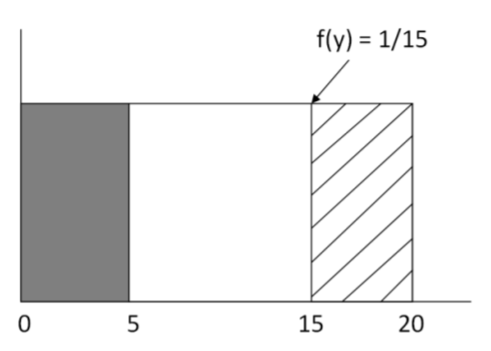
The Sounder commuter train⁶⁹ from Lakeview to Seattle, Washington arrives at Tacoma station every 20 minutes during the morning rush hour. Assume that this train is running on time.

1. Find the expected  waiting time, standard deviation, nad probability density function for \(X\).
2. Find the Interquartile Range for this Random Variable. First find the \(1^{st}\) and ^{rd}\) quartiles.
3. Find the probability of waiting at least 15 minutes for the next commuter train after arriving at Tacoma Station.
4. Find conditional probabilities for the Uniform Distribution.

Solution

Let \(X\) = the waiting time for the next train to arrive. X will follow a Uniform Distribution with the minimum waiting time of 0 minutes (you just catch the train) and a maximum waiting time of 20 minutes (you just miss the train).

1.     The expected  waiting time is 10 minutes: \(\mu=\dfrac{0+20}{2}=10\)

The standard deviation is 5.77 minutes: \(\sigma^{2}=\dfrac{(20-0)^{2}}{12}=33.33 \quad \sigma=\sqrt{33.33}=5.77\)

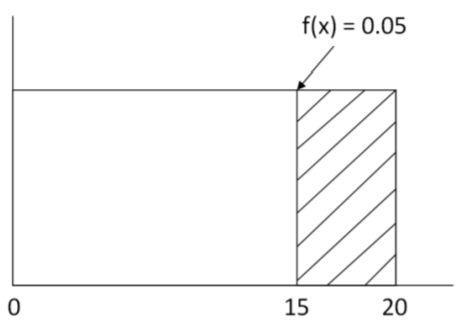
The probability density function for X is: \(f(x)=\dfrac{1}{20-0}=0.05\)

2. \(\begin{aligned}
   &Q 1=x_{25}=0+.25(20-0)=5 \\
   &Q 3=x_{75}=0+.75(20-0)=15
   \end{aligned}\)

Interquartile Range = \(Q 3-Q 1=15-5=10\) minutes

3. \(P(X \geq 15)=\dfrac{20-15}{20-0}=0.25\)

4. To find conditional probabilities for the Uniform Distribution, it easiest to just create a new Uniform Distribution from the information given.

After arriving at Tacoma Station, a commuter waits 5 minutes. Find that the probability the commuter is going to wait at least an additional 10 minutes ( a total of 15 minutes) before the next train arrives.  

The conditional probability statement can be written as \(P(X \geq 15 \mid X \geq 5)\).

Instead, simply define a new Random Variable \(Y\) = the expected total waiting time, assuming the commuter waits  at least 5 minutes.

\(a\) = minimum wait = 5 minutes

\(b\) = maximum wait = 20 minutes

\(P(Y \geq 15)=\dfrac{20-15}{20-5}=0.333\)