5.E: Testing Hypotheses (Exercises)
- Page ID
- 5437
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Chapter 5 Homework
- For each of the following questions, write the hypotheses that would be tested and then determine which hypothesis test should be used. Select from the following four choices.
\(\bullet\) 1 proportion Z test
\(\bullet\) 2 proportion Z test
\(\bullet\) 1 sample t test
\(\bullet\) 2 independent samples t test
a. Is the average commute time different when people use transit compared to if they drove?
\(H_0\):___________ \(H_1\):___________ Test: ________________________________
b. Do a majority of people eat raw cookie dough?
\(H_0\):___________ \(H_1\):___________ Test: ________________________________
c. In a statistics class, is the proportion of STEM students different than the proportion of social science student?
\(H_0\):___________ \(H_1\):___________ Test: ________________________________
d. Is the average income of a self-employed person greater than a person working for a large company?
\(H_0\):___________ \(H_1\):___________ Test: ________________________________
e. Do you average more than 7 hours of sleep a night?
\(H_0\):___________ \(H_1\):___________ Test: ________________________________
f. Is the proportion of students with student loans less than 0.60?
\(H_0\):___________ \(H_1\):___________ Test: ________________________________
g. In a long race, such as a marathon, is the difference between the second half split time faster than the first half split time. This can be phrased as: if the first split is subtracted from the second split, will the difference be less than 0? (For example, first half split: 1:06.44, second half split 1:06.01, so 1:06.01 - 1:06.44 = -0.43. The second half was faster than the first half. This is called negative splitting).
\(H_0\):___________ \(H_1\):___________ Test: ________________________________
Test the following hypotheses. Assume all assumptions for the tests have been met. Show the formulas, show the substitution and simplification, and write an appropriate concluding sentence. - When a young adult leaves home and lives on their own for the first time, they become responsible for feeding themselves. In general, there are two options, eat out or cook for themselves. Suppose someone hypothesized that the average the spent on eating out, including tax and tip, is less than $15 per day. For 30 days, they keep all their receipts and find the mean amount spent per day is $14.28 with a standard deviation of 4.6. Test the hypothesis that the mean they spend per day is less than $15.
\(\alpha = 0.05\)Write the hypotheses: \(H_0\): ___________, \(H_1\): ___________,
___________ _________________ ________________ ________________
Formula Substitution Test Statistic p-value
Fill in the blanks for the concluding sentence. At the _____ level of significance, the mean money spent per day _____ significantly less than $15 (t = ______________, p = _____________, n = ___________).
- When a child has been adopted, they may grow up wondering why their birth parents did not keep them. Technology and some changes in the laws now allow these children to find their birth parents. However, there is no guarantee the birth parent will be happy to be found. The child runs an enormous risk of being rejected. On the other hand, some birth parents are delighted to be found and fully appreciate the reunification. It has been hypothesized that a majority of the reunions have a favorable outcome. Test this hypothesis if a survey of children who found their birth parents resulted in 118 outof 179 having a favorable result. Let \(\alpha = 0.05\)
Write the hypotheses: \(H_0\): ___________, \(H_1\): ___________,
___________ _________________ ________________ ________________
Formula Substitution Test Statistic p-value
Fill in the blanks for the concluding sentence. At the ________ level of significance, the proportion of reunions that are favorable _________ significantly greater than 0.50 (\(z\) = __________, \(p\) = __________, \(n\) =_______)
- US News and World Report has stated what many think. The cheapest time to buy airline tickets is on Tuesdays after 3 pm Eastern time. money.usnews.com/money/personal- finance/articles/2012/04/18/8-insider-secrets-to-booking-cheap-airfare viewed 4-30-17. Use the data in the table below to determine if the mean difference between the Tuesday price and the price the rest of the week is less than 0.
Data was collected from Travelocity.com in May 2017 for round-trip flights on Sept 10-17 2017.Destination Airlines Day Price Tuesday Tuesday - Day Seattle to Boston Alaska Sunday 420.40 420.40 0 Chicago to Dallas United Thursday 446.40 470.40 24 San Francisco to Orlando Delta Thursday 399.60 362.60 -37 Memphis to Phoenix American Saturday 277.90 277.90 0 Denver to Las Vegas Frontier Thursday 205.95 195.98 -9.97 New York to LA Jet Blue Saturday 411.40 411.40 0 Albuquerque to Philadelphia American Sunday 513.20 513.20 0 \(H_0\): ___________, \(H_1\): ___________, \(\alpha = 0.05\)
___________ _________________ ________________ ________________
Formula Substitution Test Statistic p-value
Write the concluding sentence: - The concept of anchoring is one that makes us question our own rationality. An example of anchoring is when you see something you want to buy, but can’t afford and are then told the item is on sale. Suddenly, it looks like a good price. On the other hand, if someone told you they had bought the same item for half the price you paid, you would feel cheated. Daniel Kahneman and Amos Tversky were researchers who investigated anchoring. This concept was tested in an experiment with the Spring 2017 statistics class. The class was asked to write down the last two numbers of their phone number. Then they were asked to write down their guess for the population of Morocco. The objective is to determine if the people who wrote down numbers that were greater than or equal to 60 (last 2 digits of phone number) had a higher estimate of Morocco’s population than those with numbers less than or equal to 40. Use a level of significance of 0.10.
Write the hypotheses:
\(H_0\): ___________, \(H_1\): ___________,
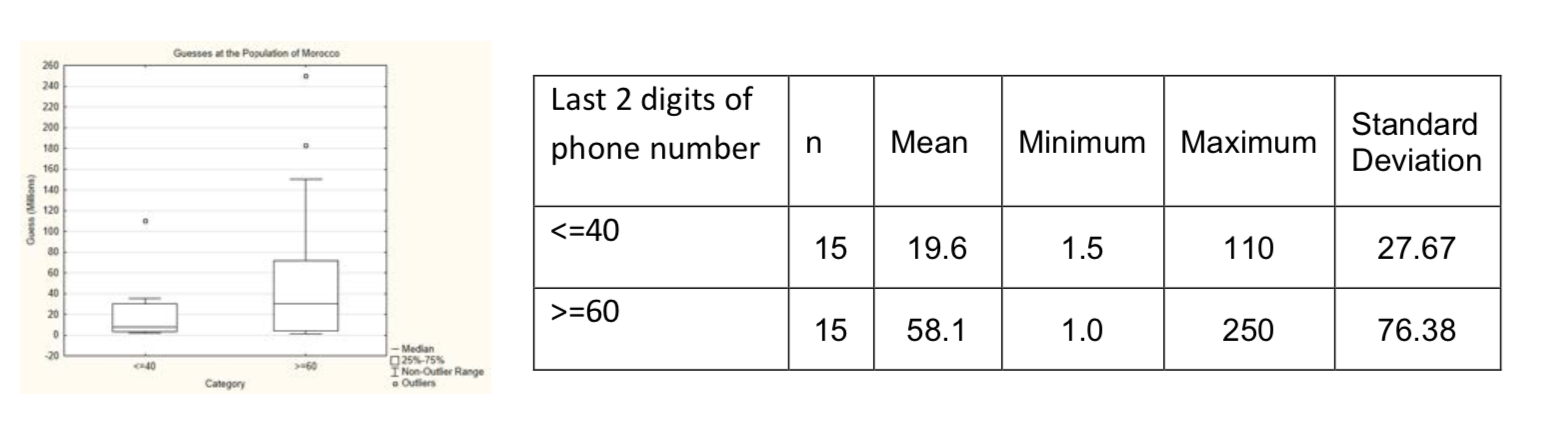
Formula Substitution
Test Statistic p-value significant?
Write the concluding sentence: - Since more people are aware of the problem of waste and are attempting to do their own part in reducing wasted bags by bringing their own reusable bags to a grocery store or not using a bag at all, is it possible that we now have fewer than half of shoppers using bags provided by the grocery store? Data: Out of 750 shoppers, 282 used a paper bag provided by the store (plastic bags are illegal in Seattle where this study by statistics students was conducted). \(\alpha = 0.05\)
\(H_0\): ___________, \(H_1\): ___________, What is the sample proportion?___________
___________ _________________ ________________ ________________
Formula Substitution Test Statistic p-value
- The Tacoma-Pierce County Health Department conducts a Healthy Youth Survey to assess the health related behaviors of Pierce County.(www.tpchd.org/resources/publi...-health-risks/) The survey is given to students in grades 6,8,10 and 12. The data from the 2002 and 2012 reports will be used to determine if there has been an increase in the use of marijuana or hashish in \(12^{\text{th}}\) grade students. Use a 5% level of significance.
a. Write the hypotheses that will be tested.
The Data: In 2012, \(x_{2012} = 165\), \(n_{2012} = 630\), \(x_{2002} = 537\), \(n_{2002} = 2184\)b. Find the sample proportions for each year. 2002_________ 2012 __________
c. Test the hypotheses.___________ _________________ ________________ ________________
Formula Substitution Test Statistic p-value
d. Write a concluding sentence. At the 5% level of significance ___________________________________________________________________________________ __________________________
e. Washington just legalized recreational use of marijuana for adults. Do you expect the use of marijuana by \(12^{\text{th}}\) graders to increase, remain the same, or decrease because of this new law? Why? Circle one: increase remain the same decrease Why? ______________________________________________________________________________________________________________
-
Briefing 5.2: Trailblazing Women
In 1966, Bobbi Gibb applied to participate in the Boston Marathon. The director wrote her back saying “women are not physiologically able to run marathon distances, and we wouldn't want to take the medical liability. “6 That was during a time when opportunities were limited for women because of the assumption they were physically incapable of doing many of the things that men could do. The brief story is that Bobbi crashed the race wearing her brother’s shorts and a sweatshirt, but within 30 seconds, some of the men realized she was a woman and where glad she was in the race.
Spectators realized it too. “As Gibb ran by the crowds, she saw their reactions. Men were cheering and clapping, and women were jumping wildly up and down and weeping.” She finished ahead of two thirds of the other runners. Six years later, the rules were changed to allow women to run in the Boston Marathon.(http://www.californiareport.org/arch...201304150850/b)Now that women are allowed to compete on an equal basis with men, we can explore the differences in performance in longer athletic events. One of the most grueling competitions is the Ironman Triathlon in which participants swim 2.4 miles, bicycle 112 miles and then run a full 26.2-mile marathon. Results from the 2013 Canadian Ironman Triathlon in Whistler, BC will be used to compare the times of the non-professional participants. The question is whether there is a significant difference in the mean times of the men and women who finished the course. Use a 5% level of significance.
a. Complete the design layout table.
Research Design Table Research Question: Type of Research Observational Study
Observational Experiment
Manipulative ExperimentWhat is the response variable? What is the parameter that will be calculated? Mean Proportion Correlation List potential confounding variables. Grouping/explanatory Variables 1 (if present) Levels: b. Write the hypotheses. \(H_0\): ___________, \(H_1\): ___________, \(\alpha = 0.05\)
Data
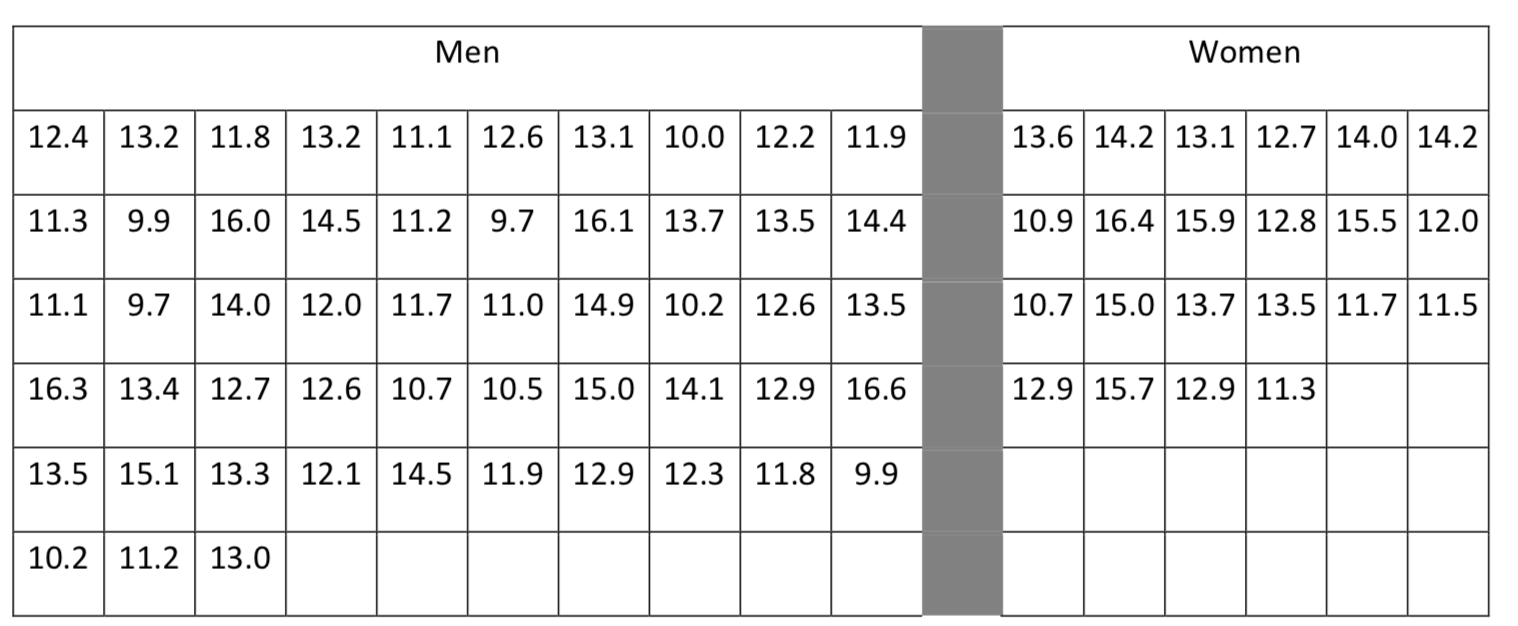
Enter the data into your calculator to find the statistics needed for 7e and 7f.
c. Make a side-by-side box plot.
d. Find the mean and standard deviation for the men and women.n mean standard deviation Men Women e. Test the hypotheses (you may use your calculator, you don’t need to write the formula).
________________ __________Test Statistic p-value
f. Write a concluding sentence.
g Based on the results of this study, what can be concluded about the physical capabilities of women compared to men in endurance activities? _________ _______________________________________ - Why Statistical Reasoning is Important for Psychology Students and Professionals In collaboration with Tom Link, Professor of Psychology Based on the research article “How Does Stigma “Get Under the Skin”?”(Hatzenbuehler, M. L., Nolen-Hoeksema, S., & Dovidio, J. (2009). How does stigma “get under the skin”? The mediating role of emotion regulation. Psychological Science, 20(10), 1282-1289.) by Mark Hatzenbuehler, Susan Nolen-Hoeksema, and John Dovidio, published in the Jorunal of the Association for Psychological Science in 2009.
This topic is taught in Psyc 100 (General Psychology) and Psyc 210 (Social Psychology)
What strategies are most effective for avoiding adverse mental health issues for victims of discrimination?
Briefing 6.3
Various groups of people feel stigma-related stress. The concept of social stigma was originally discussed by psychologist Erving Goffman in the 1963 publication Stigma: Notes on the Management of Spoiled Identity. Stigma is defined as “a set of negative and often unfair beliefs that a society or group of people have about something”. (www.merriam-webster.com 11-14-13) These groups include African Americans, LGB (lesbian, gay, bisexual), women, criminals, and obese individuals. There is some research that links stigma-related stressors to adverse mental and behavioral health. Stigma can be concealed for LGB individuals or criminals but not for the other groups. This means that people cannot tell if another person is gay unless they have been told, so the stigma is concealed from them (also called discreditable stigma). In contrast, skin color or gender is evident to another person instantly (also called discredited stigma).
Individuals subjected to discrimination have a variety of ways to respond. Two of the ways include rumination and distraction. Rumination is the process of focusing on yourself and reflecting on why you received such treatment. Distraction is to have your thoughts focused on something other than how you feel and the discrimination situation. Psychological distress, the dependent variable, will be used as a measure of mental health. It will be measured with a commonly used test.
There are three questions that will be asked in this problem. To answer these three questions, the researchers used undergraduate students and community members. The data to answer the first question will come from a daily diary the subjects maintain. The data for the second question will come from surveys given to the subjects after they wrote about a time when they were victims of discrimination. The data for the third question will be based on another survey the subjects take after they are directed towards one of the two coping mechanisms, rumination or distraction, using a random process (e.g. coin flip).
You may use your calculator to test these hypotheses. You do not need to write the formulas or show substitution.
a. Is the proportion of days with a discriminatory incident different for African Americans than it is for LGB individuals? \(\alpha = 0.05\)
African American and LGB subjects maintained a journal for 20 days.n At least one stigma- related stressor days of data African Americans 19 139 190 LGB 31 226 310 \(H_0\): ___________, \(H_1\): ___________,
Test Statistic p-value
Conclusion:
b. Is there a significant difference between the mean psychological distress score of African Americans and LGB individuals following an experiment in which the individual had to recall a discrimination issue they faced? \(\alpha = 0.05\)n Average Psychological Distress Standard Deviation African Americans 19 4.71 3.96 LGB 31 4.51 4.52 \(H_0\): ___________, \(H_1\): ___________,
Test Statistic p-value
Conclusion:
c. Is there a significant difference between the mean psychological distress score of those who used rumination to cope with the discrimination and those who used distraction?
Is there a significant difference between the psychological distress score of those who used rumination to cope with the discrimination and those who used distraction?
n Mean Standard Deviation Rumination 26 13.24 6.14 Distraction 26 10.07 4.10 \(H_0\): ___________, \(H_1\): ___________,
Test Statistic p-value
Conclusion:
d. The subjects in this research were undergraduate students and community members living near Yale University in Connecticut. Does this affect the conclusions that have been drawn? Why or why not?


