11.2: Chi-Square One-Sample Goodness-of-Fit Tests
- Page ID
- 514
- To understand how to use a chi-square test to judge whether a sample fits a particular population well.
Suppose we wish to determine if an ordinary-looking six-sided die is fair, or balanced, meaning that every face has probability \(1/6\) of landing on top when the die is tossed. We could toss the die dozens, maybe hundreds, of times and compare the actual number of times each face landed on top to the expected number, which would be \(1/6\) of the total number of tosses. We wouldn’t expect each number to be exactly \(1/6\) of the total, but it should be close. To be specific, suppose the die is tossed \(n=60\) times with the results summarized in Table \(\PageIndex{1}\). For ease of reference we add a column of expected frequencies, which in this simple example is simply a column of \(10s\). The result is shown as Table \(\PageIndex{2}\). In analogy with the previous section we call this an “updated” table. A measure of how much the data deviate from what we would expect to see if the die really were fair is the sum of the squares of the differences between the observed frequency \(O\) and the expected frequency \(E\) in each row, or, standardizing by dividing each square by the expected number, the sum
\[\dfrac{Σ(O−E)^2}{E} \nonumber \]
If we formulate the investigation as a test of hypotheses, the test is
\[H_0: \text{The die is fair}\\ vs.\\ H_a: \text{The die is not fair} \nonumber \]
| Die Value | Assumed Distribution | Observed Frequency |
|---|---|---|
| \(1\) | \(1/6\) | \(9\) |
| \(2\) | \(1/6\) | \(15\) |
| \(3\) | \(1/6\) | \(9\) |
| \(4\) | \(1/6\) | \(8\) |
| \(5\) | \(1/6\) | \(6\) |
| \(6\) | \(1/6\) | \(13\) |
| Die Value | Assumed Distribution | Observed Freq. | Expected Freq. |
|---|---|---|---|
| \(1\) | \(1/6\) | \(9\) | \(10\) |
| \(2\) | \(1/6\) | \(15\) | \(10\) |
| \(3\) | \(1/6\) | \(9\) | \(10\) |
| \(4\) | \(1/6\) | \(8\) | \(10\) |
| \(5\) | \(1/6\) | \(6\) | \(10\) |
| \(6\) | \(1/6\) | \(13\) | \(10\) |
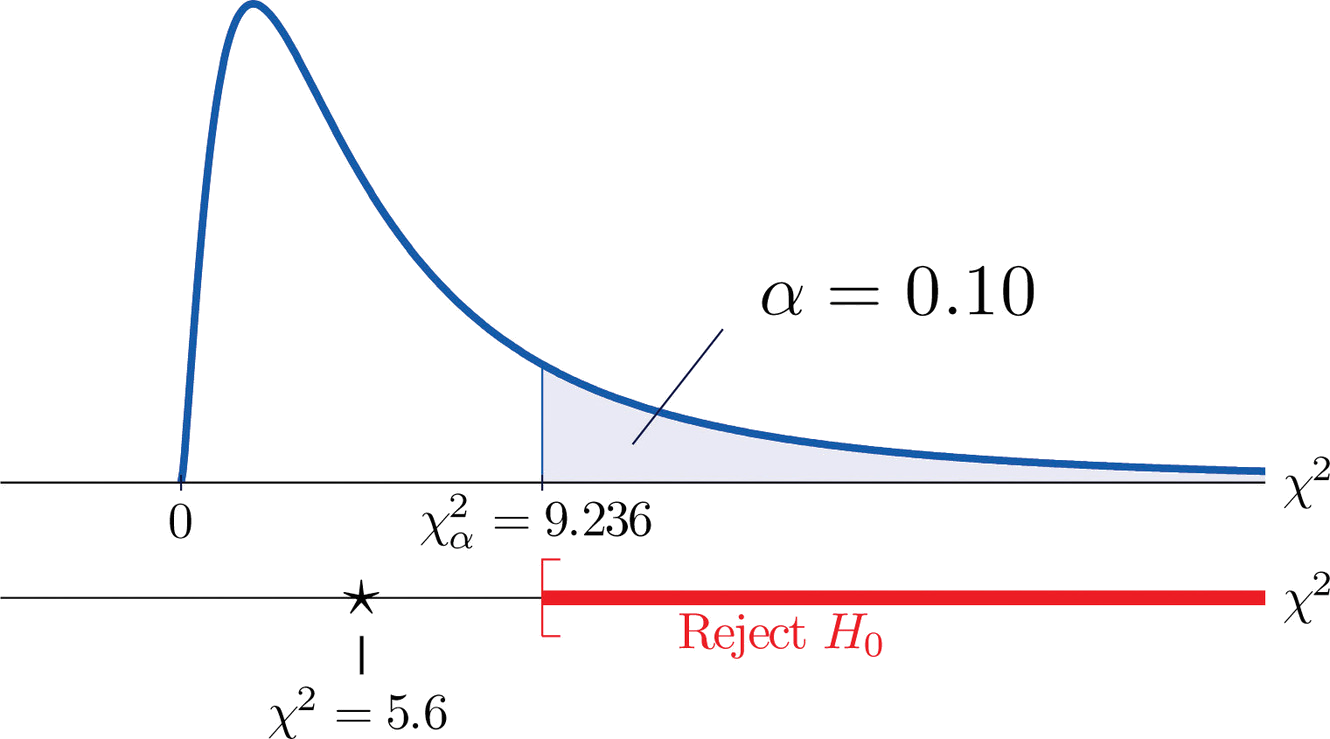
We would reject the null hypothesis that the die is fair only if the number \(\dfrac{Σ(O−E)^2}{E}\) is large, so the test is right-tailed. In this example the random variable \(\dfrac{Σ(O−E)^2}{E}\) has the chi-square distribution with five degrees of freedom. If we had decided at the outset to test at the \(10\%\) level of significance, the critical value defining the rejection region would be, reading from Figure 7.1.6, \(\chi _{\alpha }^{2}=\chi _{0.10}^{2}=9.236\), so that the rejection region would be the interval \[[9.236,\infty ) \nonumber \]. When we compute the value of the standardized test statistic using the numbers in the last two columns of Table \(\PageIndex{2}\), we obtain
\[\begin{align*} \sum \frac{(O-E)^2}{E} &= \frac{(-1)^2}{10}+\frac{(5)^2}{10}+\frac{(-1)^2}{10}+\frac{(-2)^2}{10}+\frac{(-4)^2}{10}+\frac{(3)^2}{10}\\ &= 0.1+2.5+0.1+0.4+1.6+0.9\\ &= 5.6 \end{align*} \nonumber \]
Since \(5.6<9.236\) the decision is not to reject \(H_0\). See Figure \(\PageIndex{1}\). The data do not provide sufficient evidence, at the \(10\%\) level of significance, to conclude that the die is loaded.
In the general situation we consider a discrete random variable that can take \(I\) different values, \(x_1,\: x_2,\cdots ,x_I\), for which the default assumption is that the probability distribution is
\[\begin{array}{c|c c c c} x & x_1 & x_2 & \cdots & x_I \\ \hline P(x) &p_1 &p_2 &\cdots &p_I\\ \end{array} \nonumber \]
We wish to test the hypotheses:
\[H_0: \text{The assumed probability distribution for X is valid}\\ vs.\\ H_a: \text{The assumed probability distribution for X is not valid} \nonumber \]
We take a sample of size \(n\) and obtain a list of observed frequencies. This is shown in Table \(\PageIndex{3}\). Based on the assumed probability distribution we also have a list of assumed frequencies, each of which is defined and computed by the formula
\[Ei=n×pi \nonumber \]
| Factor Levels | Assumed Distribution | Observed Frequency |
|---|---|---|
| \(1\) | \(p_1\) | \(O_1\) |
| \(2\) | \(p_2\) | \(O_2\) |
| \(\vdots\) | \(\vdots\) | \(\vdots\) |
| \(I\) | \(p_I\) | \(O_I\) |
Table \(\PageIndex{3}\) is updated to Table \(\PageIndex{4}\) by adding the expected frequency for each value of \(X\). To simplify the notation we drop indices for the observed and expected frequencies and represent Table \(\PageIndex{4}\) by Table \(\PageIndex{5}\).
| Factor Levels | Assumed Distribution | Observed Freq. | Expected Freq. |
|---|---|---|---|
| \(1\) | \(p_1\) | \(O_1\) | \(E_1\) |
| \(2\) | \(p_2\) | \(O_2\) | \(E_2\) |
| \(\vdots\) | \(\vdots\) | \(\vdots\) | \(\vdots\) |
| \(I\) | \(p_I\) | \(O_I\) | \(E_I\) |
| Factor Levels | Assumed Distribution | Observed Freq. | Expected Freq. |
|---|---|---|---|
| \(1\) | \(p_1\) | \(O\) | \(E\) |
| \(2\) | \(p_2\) | \(O\) | \(E\) |
| \(\vdots\) | \(\vdots\) | \(\vdots\) | \(\vdots\) |
| \(I\) | \(p_I\) | \(O\) | \(E\) |
Here is the test statistic for the general hypothesis based on Table \(\PageIndex{5}\), together with the conditions that it follow a chi-square distribution.
\[\chi ^2 =\sum \frac{(O-E)^2}{E} \nonumber \]
where the sum is over all the rows of the table (one for each value of \(X\)).
If
- the true probability distribution of \(X\) is as assumed, and
- the observed count \(O\) of each cell in Table \(\PageIndex{5}\) is at least \(5\),
then \(\chi ^2\) approximately follows a chi-square distribution with \(df=I-1\) degrees of freedom.
The test is known as a goodness-of-fit \(\chi ^2\) test since it tests the null hypothesis that the sample fits the assumed probability distribution well. It is always right-tailed, since deviation from the assumed probability distribution corresponds to large values of \(\chi ^2\).
Testing is done using either of the usual five-step procedures.
Table \(\PageIndex{6}\) shows the distribution of various ethnic groups in the population of a particular state based on a decennial U.S. census. Five years later a random sample of \(2,500\) residents of the state was taken, with the results given in Table \(\PageIndex{7}\) (along with the probability distribution from the census year). Test, at the \(1\%\) level of significance, whether there is sufficient evidence in the sample to conclude that the distribution of ethnic groups in this state five years after the census had changed from that in the census year.
| Ethnicity | White | Black | Amer.-Indian | Hispanic | Asian | Others |
|---|---|---|---|---|---|---|
| Proportion | \(0.743\) | \(0.216\) | \(0.012\) | \(0.012\) | \(0.008\) | \(0.009\) |
| Ethnicity | Assumed Distribution | Observed Frequency |
|---|---|---|
| White | \(0.743\) | \(1732\) |
| Black | \(0.216\) | \(538\) |
| American-Indian | \(0.012\) | \(32\) |
| Hispanic | \(0.012\) | \(42\) |
| Asian | \(0.008\) | \(133\) |
| Others | \(0.009\) | \(23\) |
Solution
We test using the critical value approach.
- Step 1. The hypotheses of interest in this case can be expressed as \[H_0: \text{The distribution of ethnic groups has not changed}\\ vs.\\ H_a: \text{The distribution of ethnic groups has changed} \nonumber \]
- Step 2. The distribution is chi-square.
- Step 3. To compute the value of the test statistic we must first compute the expected number for each row of Table \(\PageIndex{7}\). Since \(n=2500\), using the formula \(E_i=n\times p_i\) and the values of \(p_i\) from either Table \(\PageIndex{6}\) or Table \(\PageIndex{7}\), \[E_1=2500×0.743=1857.5\\ E_2=2500×0.216=540\\ E_3=2500×0.012=30\\ E_4=2500×0.012=30\\ E_5=2500×0.008=20\\ E_6=2500×0.009=22.5 \nonumber \]
Table \(\PageIndex{7}\) is updated to Table \(\PageIndex{8}\).
| Ethnicity | Assumed Dist. | Observed Freq. | Expected Freq. |
|---|---|---|---|
| White | \(0.743\) | \(1732\) | \(1857.5\) |
| Black | \(0.216\) | \(538\) | \(540\) |
| American-Indian | \(0.012\) | \(32\) | \(30\) |
| Hispanic | \(0.012\) | \(42\) | \(30\) |
| Asian | \(0.008\) | \(133\) | \(20\) |
| Others | \(0.009\) | \(23\) | \(22.5\) |
The value of the test statistic is
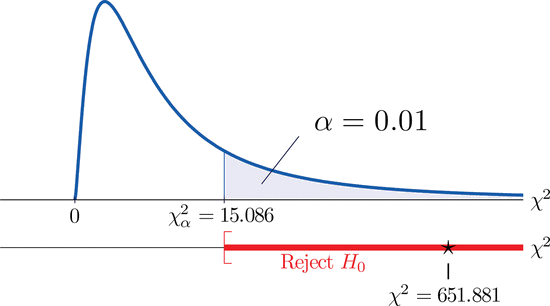
\[\begin{align*} \chi ^2 &= \sum \frac{(O-E)^2}{E}\\ &= \frac{(1732-1857.5)^2}{1857.5}+\frac{(538-540)^2}{540}+\frac{(32-30)^2}{30}+\frac{(42-30)^2}{30}+\frac{(133-20)^2}{20}+\frac{(23-22.5)^2}{22.5}\\ &= 651.881 \end{align*} \nonumber \]
Since the random variable takes six values, \(I=6\). Thus the test statistic follows the chi-square distribution with \(df=6-1=5\) degrees of freedom.
Since the test is right-tailed, the critical value is \(\chi _{0.01}^{2}\). Reading from Figure 7.1.6, \(\chi _{0.01}^{2}=15.086\), so the rejection region is \([15.086,\infty )\).
Since \(651.881>15.086\) the decision is to reject the null hypothesis. See Figure \(\PageIndex{2}\). The data provide sufficient evidence, at the \(1\%\) level of significance, to conclude that the ethnic distribution in this state has changed in the five years since the U.S. census.
- The chi-square goodness-of-fit test can be used to evaluate the hypothesis that a sample is taken from a population with an assumed specific probability distribution.


