10.2: Rank Abundance Graphs and Habitat Suitability Index
- Page ID
- 2933
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Rank Abundance Graphs
Species abundance distribution can also be expressed through rank abundance graphs. A common approach is to plot some measure of species abundance against their rank order of abundance. Such a plot allows the user to compare not only relative richness but also evenness. Species abundance models (also called abundance curves) use all available community information to create a mathematical model that describes the number and relative abundance of all species in a community. These models include the log normal, geometric, logarithmic, and MacArthur’s brokenstick model. Many ecologists use these models as a way to express resource partitioning where the abundance of a species is equivalent to the percentage of space it occupies (Magurran 1988). Abundance curves offer an alternative to single number diversity indices by graphically describing community structure.
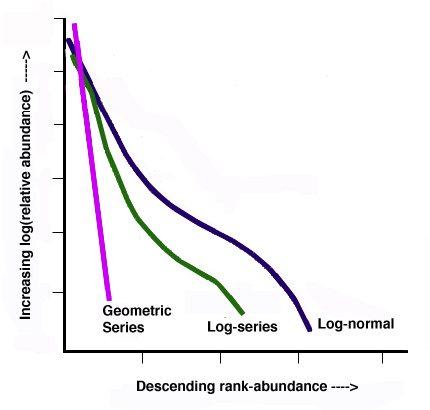
Figure \(\PageIndex{1}\). Generic Rank-abundance diagram of three common mathematical models used to fit species abundance distributions: Motomura’s geometric series, Fisher’s logseries, and Preston’s log-normal series (modified from Magurran 1988) by Aedrake09.
Let’s compare the indices and a very simple abundance distribution in two different situations. Stand A and B both have the same number of species (same richness), but the number of individuals in each species is more similar in Stand A (greater evenness). In Stand B, species 1 has the most individuals, with the remaining nine species having a substantially smaller number of individuals per species. Richness, the compliment to Simpson’s D, and Shannon’s H’ are computed for both stands. These two diversity indices incorporate both richness and evenness. In the abundance distribution graph, richness can be compared on the x-axis and evenness by the shape of the distribution. Because Stand A displays greater evenness it has greater overall diversity than Stand B. Notice that Stand A has higher values for both Simpson’s and Shannon’s indices compared to Stand B.
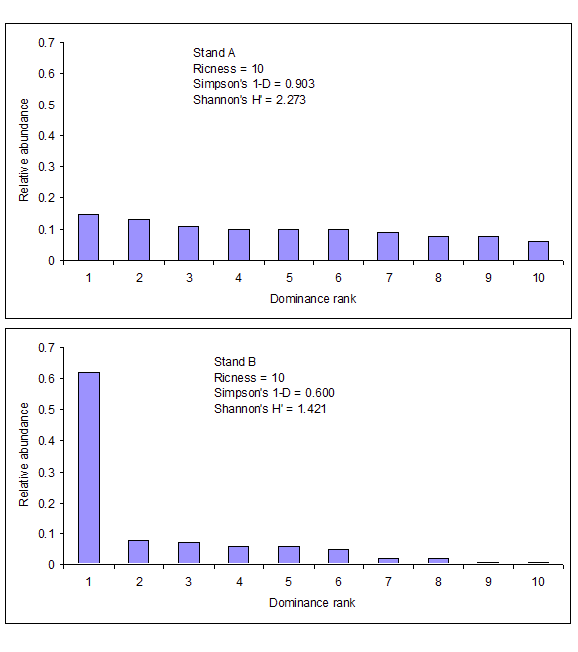
Figure \(\PageIndex{2}\). Two stands comparing richness, Simpson’s D, and Shannon’s index.
Indices of diversity vary in computation and interpretation so it is important to make sure you understand which index is being used to measure diversity. It is unsuitable to compare diversity between two areas when different indices are computed for each area. However, when multiple indices are computed for each area, the sampled areas will rank similarly in diversity as measured by the different indices. Notice in this previous example both Simpson’s and Shannon’s index rank Stand A as more diverse and Stand B as less diverse.
Similarity between Sites
There are also indices that compare the similarity (and dissimilarity) between sites. The ideal objective is to express the ecological similarity of different sites; however, it is important to identify the aim or focus of the investigation in order to select the most appropriate index. While many indices are available, van Tongeren (1995) states that most of the indices do not have a firm theoretical basis and suggests that practical experience should guide the selection of available indices.
The Jaccard index (1912) compares two sites based on the presence or absence of species and is used with qualitative data (e.g., species lists). It is based on the idea that the more species both sites have in common, the more similar they are. The Jaccard index is the proportion of species out of the total species list of the two sites, which is common to both sites:
\[SJ = \frac {c} {(a + b + c)}\]
where SJ is the similarity index, c is the number of shared species between the two sites and a and b are the number of species unique to each site. Sørenson (1948) developed a similarity index that is frequently referred to as the coefficient of community (CC):
\[CC = \frac {2c} {(a + b + 2c)}\]
As you can see, this index differs from Jaccard’s in that the number of species shared between the two sites is divided by the average number of species instead of the total number of species for both sites. For both indices, the higher the value the more ecologically similar two sites are.
If quantitative data are available, a similarity ratio (Ball 1966) or a percentage similarity index, such as Gauch (1982), can be computed. Not only do these indices compare number of similar and dissimilar species present between two sites, but also incorporate abundance. The similarity ratio is:
\[SR_{ij} = \dfrac {\sum y_{ki}y_{kj}}{\sum y_{ki}^2 +\sum y_{kj}^2 -\sum(y_{ki}y_{kj})}\]
where yki is the abundance of the kth species at site i (sites i and j are compared). Notice that this equation resolves to Jaccard’s index when just presence or absence data is available. The percent similarity index is:
\[PS_{ij} = \dfrac {200\sum min (y_{ki},y_{kj})} {\sum y_{ki}+\sum y_{kj}}\]
Again, notice how this equation resolves to Sørenson’s index with qualitative data only. So let’s look at a simple example of how these indices allow us to compare similarity between three sites. The following example presents hypothetical data on species abundance from three different sites containing seven different species (A-G).
|
Site |
|||
|
Species |
1 |
2 |
3 |
|
A |
4 |
0 |
1 |
|
B |
0 |
1 |
0 |
|
C |
0 |
0 |
0 |
|
D |
1 |
0 |
1 |
|
E |
1 |
4 |
0 |
|
F |
3 |
1 |
1 |
|
G |
1 |
0 |
3 |
Let’s begin by computing Jaccard’s and Sørenson’s indices for the three comparisons (site 1 vs. site 2, site 1 vs. site 3, and site 2 vs. site 3).
\(SJ1,2=\frac {2}{(3+1+2)}=0.33\) \(SJ1,3 = \frac {4}{(4+1+0)}=0.80\) \(SJ2,3 =\frac {1}{(1+2+3)} = 0.17 \nonumber \)
\(CC1,2=\frac {2(2)}{(3+1+2(2))} = 0.50\) \(CC1,3 =\frac {2(4)}{(1+0+2(4))} = 0.89\) \(CC2,3 =\frac {2(1)}{(2+3+2(1))} = 0.29 \nonumber \)
Both of these qualitative indices declare that sites 1 and 3 are the most similar and sites 2 and 3 are the least similar. Now let’s compute the similarity ratio and the percent similarity index for the same site comparisons.
\[SR1,2=\dfrac {[(4 \times 0)+(0 \times 1) +(0\times 0)+(1\times 0)+(1\times4)+(3\times 1)+(1\times 0)]}{(4^2+0^2+0^2+1^2+1^2+3^2+1^2)+(0^0+1^2+0^2+0^2+4^2+1^2+0^2)+(4 \times 0)+(0 \times 1) +(0\times 0)+(1\times 0)+(1\times4)+(3\times 1)+(1\times 0)} \nonumber \]
\[SR1,2= 0.23\]
\[SR1,3=\dfrac {[(4\times 1)+(0\times 0)+(0\times 0)+(1\times 1)+(1\times 0)+(3\times 1)+(1\times 3)]}{(4^2 +0^2+0^2+1^2+1^2+3^2+1^2)+(1^2+0^2+0^2+1^2+0^2+1^2+3^2)+(4\times 1)+(0\times 0)+(0\times 0)+(1\times 1)+(1\times 0)+(3\times 1)+(1\times 3)} \nonumber \]
\[SR1,3= 0.38\]
\[SR2,3=\dfrac {[(0\times 1)+(1\times 0)+(0\times 0)+(0\times 1) +(4\times 0) +(1\times 1) +(0\times 3)]}{(0^2+1^2+0^2+0^2+4^2+1^2+0^2)+(1^2+0^2+0^2+1^2+0^2+1^2+3^2)+(0\times 1)+(1\times 0)+(0\times 0)+(0\times 1) +(4\times 0) +(1\times 1) +(0\times 3)} \nonumber \]
\[SR1,3= 0.03\]
\[PS1,2=\dfrac {200(0+0+0+0+1+1+0)}{(4+0+0+1+1+3+1)+(0+1+0+0+4+1+0)}=25.0 \nonumber \]
\[PS1,3=\dfrac {200(1+0+0+1+0+1+1)}{(4+0+0+1+1+3+1)+(1+0+0+1+0+1+3)} = 50.0 \nonumber \]
\[PS2,3=\dfrac {200(0+0+0+0+0+1+0)}{(0+1+0+0+4+1+0)+(1+0+0+1+0+1+3)} = 16.7 \nonumber \]
A matrix of percent similarity values allows for easy interpretation (especially when comparing more than three sites).
\[\begin{array}{c|cc}
& \mathbf{1} & \mathbf{2} \\
\hline \mathbf{2} & 25.0 & \\
\mathbf{3} & 50.0 & 16.7
\end{array} \nonumber \]
Table \(\PageIndex{1}\). A matrix of percent similarity for three sites.
The quantitative indices return the same conclusions as the qualitative indices. Sites 1 and 3 are the most similar ecologically, and sites 2 and 3 are the least similar; and also site 2 is most unlike the other two sites.
Habitat Suitability Index (HSI)
In 1980, the U.S. Fish and Wildlife Service (USFWS) developed a procedure for documenting predicted impacts to fish and wildlife from proposed land and water resource development projects. The Habitat Evaluation Procedures (HEP) (Schamberger and Farmer 1978) were developed in response to the need to document the non-monetary value of fish and wildlife resources. HEP incorporates population and habitat theories for each species and is based on the assumption that habitat quality and quantity can be numerically described so that changes to the area could be assessed and compared. It is a species-habitat approach to impact assessment and habitat quality, for a specific species is quantified using a habitat suitability index (HSI).
Habitat suitability index (HSI) models provide a numerical index of habitat quality for a specific species (Schamberger et al. 1982) and in general assume a positive, linear relationship between carrying capacity (number of animals supported by some unit area) and HSI. Today’s natural resource manager often faces economically and socially important decisions that will affect not only timber but wildlife and its habitat. HSI models provide managers with tools to investigate the requirements necessary for survival of a species. Understanding the relationships between animal habitat and forest management prescription is vital towards a more comprehensive management approach of our natural resources. An HSI model synthesizes habitat use information into a framework appropriate for fieldwork and is scaled to produce an index value between 0.0 (unsuitable habitat) to 1.0 (optimum habitat), with each increment of change being identical to another. For example, a change in HSI from 0.4 to 0.5 represents the same magnitude of change as from 0.7 to 0.8. The HSI values are multiplied by area of available habitat to obtain Habitat Units (HUs) for individual species. The U.S. Fish and Wildlife Service (USFWS) has documented a series of HSI models for a wide variety of species (FWS/OBS-82/10).
Let’s examine a simple HSI model for the marten (Martes americana) which inhabits late successional forest communities in North America (Allen 1982). An HSI model must begin with habitat use information, understanding the species needs in terms of food, water, cover, reproduction, and range for this species. For this species, the winter cover requirements are more restrictive than cover requirements for any other season so it was assumed that if adequate winter cover was available, habitat requirements for the rest of the year would not be limiting. Additionally, all winter habitat requirements are satisfied in boreal evergreen forests. Given this, the research identified four crucial variables for winter cover that needed to be included in the model.

Figure \(\PageIndex{3}\). Habitat requirements for the marten.
For each of these four winter cover variables (V1, V2, V3, and V4), suitability index graphs were created to examine the relationship between various conditions of these variables and suitable habitat for the marten. A reproduction of the graph for % tree canopy closure is presented below.
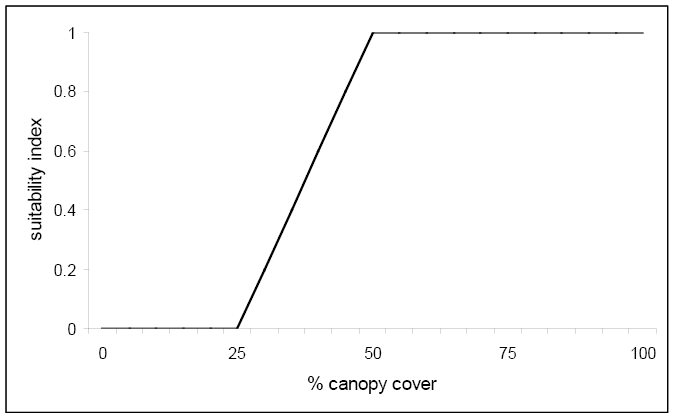
Figure \(\PageIndex{4}\). Suitability index graph for percent canopy cover.
Notice that any canopy cover less than 25% results in unacceptable habitat based on this variable alone. However, once 50% canopy cover is reached the suitability index reaches 1.0 and optimum habitat for this variable is achieved. The following equation was created that combined the life requisite values for the marten using these four variables:
\[\frac{(V_1 \times V_2 \times V_3 \times V_4)} {2} \nonumber \]
Since winter cover was the only life requisite considered in this model, the HSI equals the winter cover value. As you can see, the more life requisites included in the model, the more complex the model becomes.
While HSI values identify the quality of the habitat for a specific species, wildlife diversity as a whole is a function of size and spatial arrangement of the treated stands (Porter 1986). Horizontal and structural diversity are important. Generally speaking, the more stands of different character an area contains, the greater the wildlife diversity. The spatial distribution of differing types of stands supports animals that need multiple cover types. In order to promote wildlife species diversity, a manager must develop forest management prescription that varies the spatial and temporal patterns of timber reproduction, thereby providing greater horizontal and vertical structural diversity.
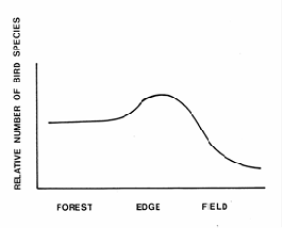
Figure \(\PageIndex{5}\): Bird species diversity nesting across a forest to field gradient (After Strelke and Dickson 1980).
Typically, even-aged management reduces vertical structural diversity, but options such as the shelterwood method tend to mitigate this problem. Selection system tends to promotes both horizontal and vertical diversity.
Integrated natural resource management can be a complicated process but not impossible. Vegetation response to silvicultural prescriptions provides the foundation for understanding the wildlife response. By examining the present characteristics of the managed stands, understanding the future response due to management, and comparing those with the requirements of specific species, we can achieve habitat manipulation together with timber management.


