7.2: Simple Linear Regression
- Page ID
- 2912
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Once we have identified two variables that are correlated, we would like to model this relationship. We want to use one variable as a predictor or explanatory variable to explain the other variable, the response or dependent variable. In order to do this, we need a good relationship between our two variables. The model can then be used to predict changes in our response variable. A strong relationship between the predictor variable and the response variable leads to a good model.
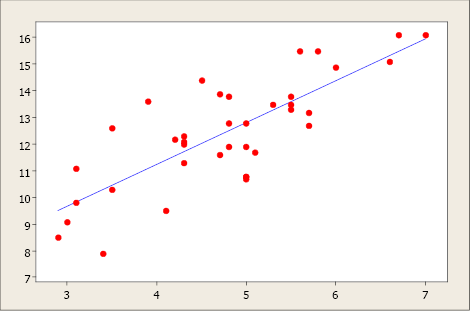
Figure \(\PageIndex{1}\). Scatterplot with regression model.
A simple linear regression model is a mathematical equation that allows us to predict a response for a given predictor value.
Our model will take the form of \(\hat y = b_0+b_1x\) where b0 is the y-intercept, b1 is the slope, x is the predictor variable, and ŷ an estimate of the mean value of the response variable for any value of the predictor variable.
The y-intercept is the predicted value for the response (y) when x = 0. The slope describes the change in y for each one unit change in x. Let’s look at this example to clarify the interpretation of the slope and intercept.
A hydrologist creates a model to predict the volume flow for a stream at a bridge crossing with a predictor variable of daily rainfall in inches.
- Answer
-
\[\hat y = 1.6 +29 x \nonumber\]
The y-intercept of 1.6 can be interpreted this way: On a day with no rainfall, there will be 1.6 gal. of water/min. flowing in the stream at that bridge crossing. The slope tells us that if it rained one inch that day the flow in the stream would increase by an additional 29 gal./min. If it rained 2 inches that day, the flow would increase by an additional 58 gal./min.
What would be the average stream flow if it rained 0.45 inches that day?
- Answer
-
\[\hat y= 1.6 + 29x = 1.6 + 29(0.45) = 14.65 gal./min \nonumber\]
The Least-Squares Regression Line (shortcut equations)
The equation is given by
\[\hat y = b_0+b_1x\]
where \(b_1 = r\left ( \dfrac {s_y}{s_x} \right )\) is the slope and \(b_0=\hat y -b_1\bar x\) is the y-intercept of the regression line.
An alternate computational equation for slope is:
\[b_1 = \dfrac {\sum xy - \dfrac {(\sum x)(\sum y)}{n}} {\sum x^2 - \dfrac {(\sum x)^2}{n}} = \dfrac {S_{xy}}{S_{xx}}\]
This simple model is the line of best fit for our sample data. The regression line does not go through every point; instead it balances the difference between all data points and the straight-line model. The difference between the observed data value and the predicted value (the value on the straight line) is the error or residual. The criterion to determine the line that best describes the relation between two variables is based on the residuals.
\[Residual = Observed – Predicted\]
For example, if you wanted to predict the chest girth of a black bear given its weight, you could use the following model.
Chest girth = 13.2 +0.43 weight
The predicted chest girth of a bear that weighed 120 lb. is 64.8 in.
Chest girth = 13.2 + 0.43(120) = 64.8 in.
But a measured bear chest girth (observed value) for a bear that weighed 120 lb. was actually 62.1 in.
The residual would be 62.1 – 64.8 = -2.7 in.
A negative residual indicates that the model is over-predicting. A positive residual indicates that the model is under-predicting. In this instance, the model over-predicted the chest girth of a bear that actually weighed 120 lb.
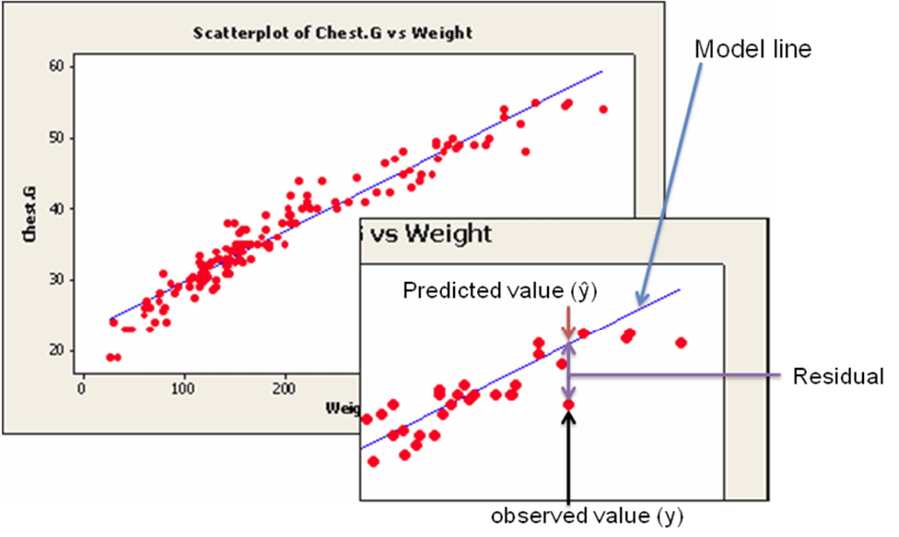
Figure \(\PageIndex{2}\). Scatterplot with regression model illustrating a residual value.
This random error (residual) takes into account all unpredictable and unknown factors that are not included in the model. An ordinary least squares regression line minimizes the sum of the squared errors between the observed and predicted values to create a best fitting line. The differences between the observed and predicted values are squared to deal with the positive and negative differences.
Coefficient of Determination
After we fit our regression line (compute b0 and b1), we usually wish to know how well the model fits our data. To determine this, we need to think back to the idea of analysis of variance. In ANOVA, we partitioned the variation using sums of squares so we could identify a treatment effect opposed to random variation that occurred in our data. The idea is the same for regression. We want to partition the total variability into two parts: the variation due to the regression and the variation due to random error. And we are again going to compute sums of squares to help us do this.
Suppose the total variability in the sample measurements about the sample mean is denoted by \(\sum (y_i - \bar y)^2\), called the sums of squares of total variability about the mean (SST). The squared difference between the predicted value \(\hat y\) and the sample mean is denoted by \(\sum (\hat {y_i} - \bar y)^2\), called the sums of squares due to regression (SSR). The SSR represents the variability explained by the regression line. Finally, the variability which cannot be explained by the regression line is called the sums of squares due to error (SSE) and is denoted by \(\sum (y_i - \hat y)^2\). SSE is actually the squared residual.
|
SST |
= SSR |
+ SSE |
|
\(\sum (y_i - \bar y)^2\) |
= \(\sum (\hat {y_i} - \bar y)^2\) |
+\(\sum (\hat {y_i} - \bar y)^2\) |
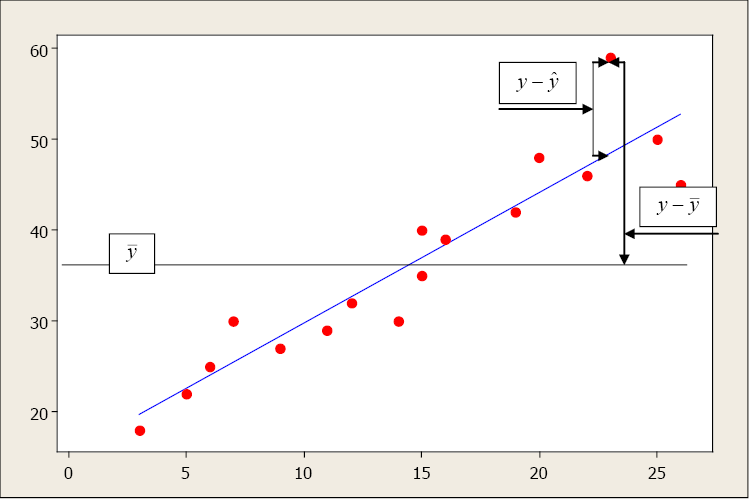
Figure \(\PageIndex{3}\). An illustration of the relationship between the mean of the y’s and the predicted and observed value of a specific y.
The sums of squares and mean sums of squares (just like ANOVA) are typically presented in the regression analysis of variance table. The ratio of the mean sums of squares for the regression (MSR) and mean sums of squares for error (MSE) form an F-test statistic used to test the regression model.
The relationship between these sums of square is defined as
\[Total \ Variation = Explained \ Variation + Unexplained \ Variation\]
The larger the explained variation, the better the model is at prediction. The larger the unexplained variation, the worse the model is at prediction. A quantitative measure of the explanatory power of a model is \(R^2\), the Coefficient of Determination:
\[R^2 = \dfrac {Explained \ Variation}{Total \ Variation}\]
The Coefficient of Determination measures the percent variation in the response variable (y) that is explained by the model.
- Values range from 0 to 1.
- An \(R^2\) close to zero indicates a model with very little explanatory power.
- An \(R^2\) close to one indicates a model with more explanatory power.
The Coefficient of Determination and the linear correlation coefficient are related mathematically.
\[R^2 = r^2\]
However, they have two very different meanings: r is a measure of the strength and direction of a linear relationship between two variables; R2 describes the percent variation in “y” that is explained by the model.
Residual and Normal Probability Plots
Even though you have determined, using a scatterplot, correlation coefficient and R2, that x is useful in predicting the value of y, the results of a regression analysis are valid only when the data satisfy the necessary regression assumptions.
- The response variable (y) is a random variable while the predictor variable (x) is assumed non-random or fixed and measured without error.
- The relationship between y and x must be linear, given by the model \(\hat y = b_0 + b_1x\).
- The error of random term the values ε are independent, have a mean of 0 and a common variance \(\sigma^2\), independent of x, and are normally distributed.
We can use residual plots to check for a constant variance, as well as to make sure that the linear model is in fact adequate. A residual plot is a scatterplot of the residual (= observed – predicted values) versus the predicted or fitted (as used in the residual plot) value. The center horizontal axis is set at zero. One property of the residuals is that they sum to zero and have a mean of zero. A residual plot should be free of any patterns and the residuals should appear as a random scatter of points about zero.
A residual plot with no appearance of any patterns indicates that the model assumptions are satisfied for these data.
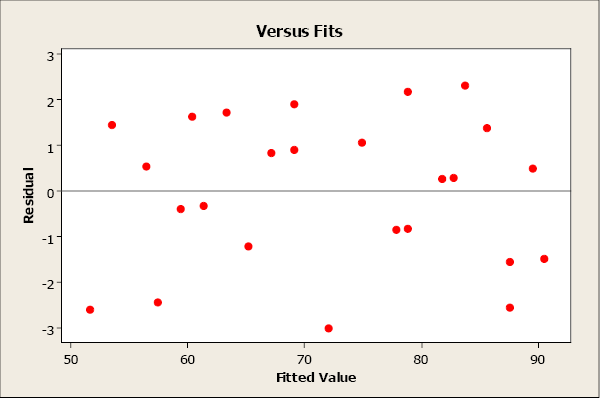
Figure \(\PageIndex{4}\). A residual plot.
A residual plot that has a “fan shape” indicates a heterogeneous variance (non-constant variance). The residuals tend to fan out or fan in as error variance increases or decreases.
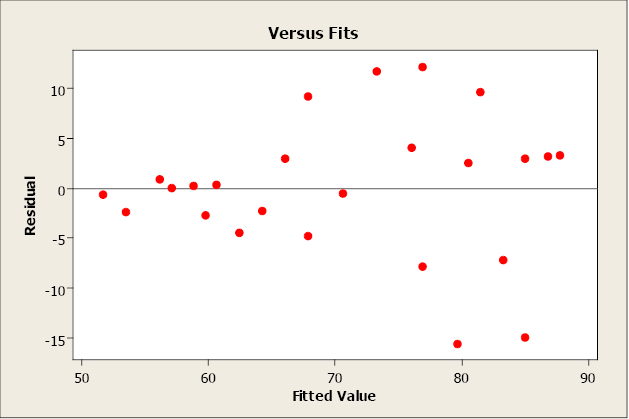
Figure \(\PageIndex{5}\). A residual plot that indicates a non-constant variance.
A residual plot that tends to “swoop” indicates that a linear model may not be appropriate. The model may need higher-order terms of x, or a non-linear model may be needed to better describe the relationship between y and x. Transformations on x or y may also be considered.
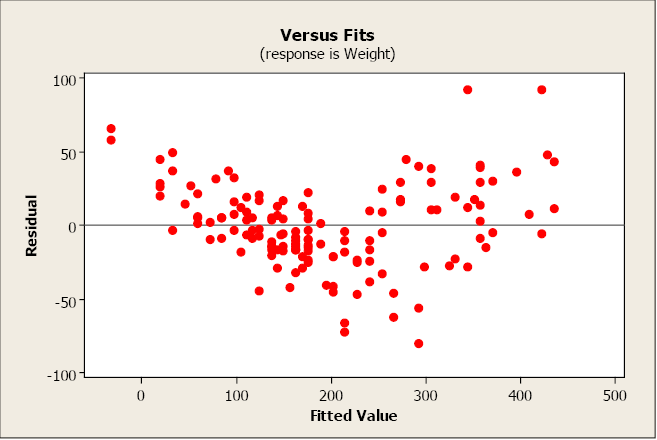
Figure \(\PageIndex{6}\). A residual plot that indicates the need for a higher order model.
A normal probability plot allows us to check that the errors are normally distributed. It plots the residuals against the expected value of the residual as if it had come from a normal distribution. Recall that when the residuals are normally distributed, they will follow a straight-line pattern, sloping upward.
This plot is not unusual and does not indicate any non-normality with the residuals.
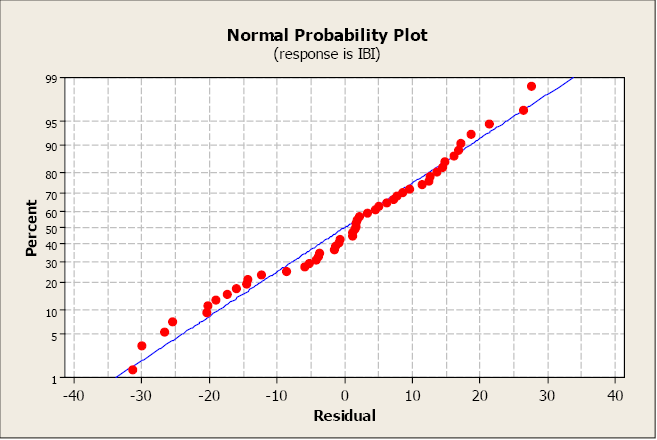
Figure \(\PageIndex{7}\). A normal probability plot.
This next plot clearly illustrates a non-normal distribution of the residuals.
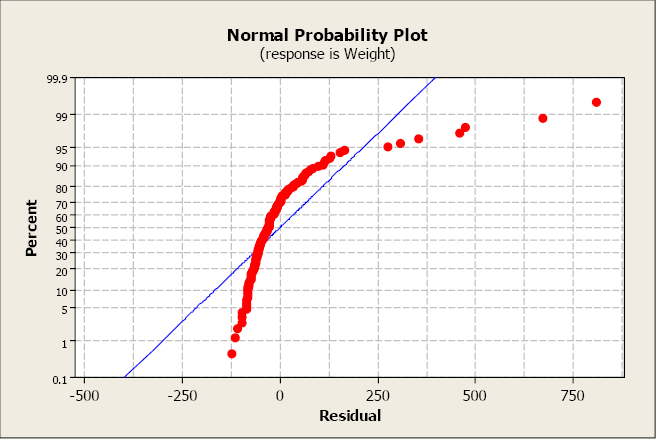
Figure \(\PageIndex{8}\). A normal probability plot, which illustrates non-normal distribution.
The most serious violations of normality usually appear in the tails of the distribution because this is where the normal distribution differs most from other types of distributions with a similar mean and spread. Curvature in either or both ends of a normal probability plot is indicative of nonnormality.


