4.4: Inferences about Two Population Proportions

Inferences about Two Population Proportions

We can apply the same methods we just learned with means to our two-sample proportion problems. We have two populations with two samples and we want to compare the population proportions.

• Is the proportion of lakes in New York with invasive species different from the proportion of lakes in Michigan with invasive species?
• Is the proportion of construction companies using certified lumber greater in the northeast than in the southeast?

A test of two population proportions is very similar to a test of two means, except that the parameter of interest is now “p” instead of “µ”. With a one-sample proportion test, we used \(\hat p =\frac {x}{n}\)as the point estimate of p. We expect that p̂ would be close to p. With a test of two proportions, we will have two p̂’s, and we expect that (p̂1 – p̂2) will be close to (p1 – p2). The test statistic accounts for both samples.

• With a one-sample proportion test, the test statistic is

\[z = \frac {\hat p - p}{\sqrt {\frac {p(1-p)}{n}}}\]

and it has an approximate standard normal distribution.

• For a two-sample proportion test, we would expect the test statistic to be

\[z=\frac {(\hat {p_1} -\hat {p_2})-(p_1-p_2)}{\sqrt {\frac {p_1(1-p_1)}{n_1}+\frac {p_2(1-p_2)}{n_2}}}\]

HOWEVER, the null hypothesis will be that p1 = p2. Because the H0 is assumed to be true, the test assumes that p1 = p2. We can then assume that p1 = p2 equals p, a common population proportion. We must compute a pooled estimate of p (its unknown) using our sample data.

\[\bar p = \frac {x_1+x_2}{n_1+n_2}\]

The test statistic then takes the form of

\[z=\frac {(\hat {p_1} -\hat {p_2})-(p_1-p_2)}{\sqrt {\frac {\bar p(1-\bar p)}{n_1}+\frac {\bar p(1-\bar p)}{n_2}}}\]

The hypothesis test follows the same steps that we have seen in previous sections:

• State the null and alternative hypotheses
• State the level of significance and determine the critical value
• Compute the test statistic
• Compare the critical value and the test statistic and state a conclusion

The assumptions that we set for a one-sample proportion test still hold true for both samples. Both must be random samples from normally distributed populations satisfying the following statements:

• \(n(p)(1 – p) \ge 10\)
• Each sample size is no more than 5% of the population size.

We can again use the same three pairs of null and alternative hypotheses. Notice that we are working with population proportions so the parameter is p.

Table \(\PageIndex{1}\). Null and alternative hypotheses.

Two-sided	Left-sided	Right=sided
\(\mathrm{H}_{\mathrm{0}}:p_1=p_2\)	\(\mathrm{H}_{\mathrm{0}}: p_1=p_2 \)	(\mathrm{H}_{\mathrm{0}}: p_1=p_2 \)
\(\mathrm{H}_1: \p_1 \neq p_2 \)	\(\mathrm{H}_1: \p_1 < p_2 \)	\(\mathrm{H}_1: \p_1> p_2 \)

The critical value comes from the standard normal table and depends on the alternative hypothesis (is the question one- or two-sided?). As usual, you must state a conclusion. You must always answer the question that is asked in the alternative hypothesis.

Example \(\PageIndex{1}\):

A researcher believes that a greater proportion of construction companies in the northeast are using certified lumber in home construction projects compared to companies in the southeast. She collected a random sample of 173 companies in the southeast and found that 86 used at least 30% certified lumber. She collected another random sample of 115 companies from the northeast and found that 68 used at least 30% certified lumber. Test the researcher’s claim that a greater proportion of companies in the northeast use at least 30% certified lumber compared to the southeast. α = 0.05.

Southeast	Northeast
\(n_1 = 173\)	\(n_2 = 115\)
\(x_1 = 86\)	\(x_2 = 68\)

Solution

Write the null and alternative hypotheses:

\(H_0: p_1 = p_2\) or \(p_1 – p_2 = 0\)

\(H_1: p_1 < p_2\)

The critical value comes from the standard normal table. It is a one-sided test, so alpha is all in the left tail. The critical value is -1.645.

Compute the point estimates

\[\hat {p_1} = \frac {86}{173}=0.497\]

\[\hat {p_2} = \frac {68}{115} = 0.591\]

Now compute p̄

\[\bar p = \frac {x_1+x_2}{n_1+n_2} = \frac {86+68}{173+115} = 0.535\]

The test statistic is

\[z=\frac {(\hat {p_1} -\hat {p_2})-(p_1-p_2)}{\sqrt {\frac {\bar p(1-\bar p)}{n_1}+\frac {\bar p(1-\bar p)}{n_2}}} = \frac {(0.497-0.591)-0}{\sqrt {\frac {0.535(1-0.535)}{173}+\frac {0.535(1-0.535)}{115}}} = -1.57\]

Now compare the critical value to the test statistic and state a conclusion.

Figure \(\PageIndex{1}\): A comparison of the critical value and the test statistic.

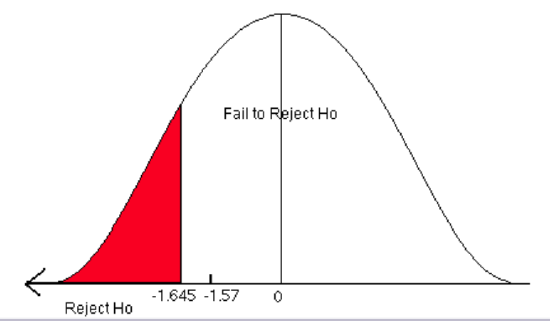
We fail to reject the null hypothesis. There is not enough evidence to support the claim that a greater proportion of companies in the northeast use at least 30% certified lumber compared to companies in the southeast.

Using the P-Value Approach

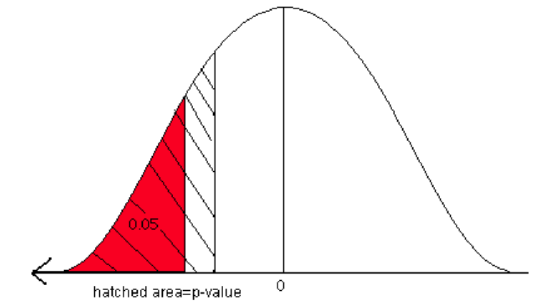
We can also answer this question using the p-value approach. The p-value is the area associated with the test statistic. This is a left-tailed problem with a test statistic of -1.57 so the p-value is the area to the left of -1.57. Look up the area associated with the Z-score -1.57 in the standard normal table.

The p-value is 0.0582.

The hatched area (p-value) is greater than the 5% level of significance (red area). We fail to reject the null hypothesis. There is not enough statistical evidence to support the claim that a greater proportion of companies in the northeast use at least 30% certified lumber compared to companies in the southeast.

Figure \(\PageIndex{2}\): Comparison of p-value and the level of significance.

Construct and Interpret a Confidence Interval about the Difference of Two Proportions

Just like a two-sample t-test about the means, we can answer this question by constructing a confidence interval about the difference of the proportions. The point estimate is \(\hat {p_1} - \hat {p_2}\). The standard error is \(\sqrt {\frac {\hat {p_1}(1-\hat {p_1})}{n_1}+\frac {\hat {p_2}(1-\hat {p_2})}{n_2}} \)and the critical value \(z_{\alpha/2}\)comes from the standard normal table.

The confidence interval takes the form of the point estimate ± the margin of error.

\[(\hat {p_1}- \hat {p_2}) \pm z_{\alpha/2} \sqrt {\frac {\hat {p_1}(1-\hat {p_1})}{n_1} + \frac {\hat {p_2}(1-\hat {p_2})}{n_2}}\]

We will use the same three steps to construct a confidence interval about the difference of the proportions. Notice the estimate of the standard error of the differences. We do not rely on the pooled estimate of p when constructing confidence intervals to estimate the difference in proportions. This is because we are not making any assumptions regarding the equality of p1 and p2, as we did in the hypothesis test.

1) critical value \(z_{\alpha/2}\)

2) \(E = z_{\alpha/2} \sqrt {\frac {\hat {p_1}(1-\hat {p_1})}{n_1}+\frac {\hat {p_2}(1-\hat {p_2}}{n_2}}\)

3) \((\hat {p_1}-\hat {p_2}) \pm E\)

Let’s revisit Ex. 6 again, but this time we will construct a confidence interval about the difference between the two proportions.

Example \(\PageIndex{2}\):

The researcher claims that a greater proportion of companies in the northeast use at least 30% certified lumber compared to companies in the southeast. We can test this claim by constructing a 90% confidence interval about the difference of the proportions.

1) critical value \(z_{\alpha/2}= 1.645\)

2) \(E = z_{\alpha/2} \sqrt {\frac {\hat {p_1}(1-\hat {p_1})}{n_1}+\frac {\hat {p_2}(1-\hat {p_2}}{n_2}}=1.645\sqrt {\frac {0.497(1-0.497)}{173}+\frac {0.591(1-0.591)}{115}}=0.098\)

3) \((\hat {p_1}-\hat {p_2}) \pm E= (0.497-0.591) ± 0.098\)

The 90% confidence interval about the difference of the proportions is (-0.192, 0.004).

BUT, this doesn’t answer the question the researcher asked. We must use one of the three interpretations seen in the previous section. In this problem, the confidence interval contains zero. Therefore we can conclude that there is no significant difference between the proportions of companies using certified lumber in the northeast and in the southeast.

Example \(\PageIndex{3}\):

A hydrologist is studying the use of Best Management Plans (BMP) in managed forest stands to protect riparian zones. He collects information from 62 stands that had a management plan by a forester and finds that 47 stands had correctly implemented BMPs to protect the riparian zones. He collected information from 58 stands that had no management plan and found that 26 of them had correctly implemented BMPs for riparian zones. Do these data suggest that there is a significant difference in the proportion of stands with and without management plans that had correct BMPs for riparian zones? α = 0.05.

Plan	No Plan
\(x_1 = 47\)	\(x_2 = 26\)
\(n_1 = 62\)	\(n_2 = 58\)

Let’s answer this question both ways by first using a hypothesis test and then by constructing a confidence interval about the difference of the proportions.

\(H_0: p_1 = p_2\) or \(p_1 – p_2 = 0\)

\(H_1: p_1 \ne p_2\)

Critical value: ±1.96

Test statistic:

\[z=\frac {(\hat {p_1}-\hat {p_2})-(p_1 - p_2)}{\sqrt {\frac {\bar p (1- \bar p)}{n_1}+\frac {\bar p(1-\bar p)}{n_2}}}= \frac {(0.758-0.448)-0}{\sqrt {\frac {0.608(1-0.608)}{62}+\frac {0.608(1-0.608)}{58}}}=3.48 \nonumber \]

The test statistic is greater than 1.96 and falls in the rejection zone. There is enough evidence to support the claim that there is a significant difference in the proportion of correctly implemented BMPs with and without management plans.

Now compute the p-value and compare it to the level of significance. The p-value is two times the area under the curve to the right of 3.48. Look for the area (in the standard normal table) associated with a Z-score of 3.48. The area to the right of 3.48 is 1 – 0.9997 = 0.0003. The p-value is 2 x 0.0003 = 0.0006.

The p-value is less than 0.05. We will reject the null hypothesis and support the claim that the proportions are different.

Now, answer this question using a confidence interval.

1) critical value \(z_{\alpha/2}= 1.96\)

2) \(E = z_{\alpha/2} \sqrt {\frac {\hat {p_1}(1-\hat {p_1})}{n_1}+\frac {\hat {p_2}(1-\hat {p_2})}{n_2}}=1.96\sqrt {\frac {0.758(1-0.758)}{62}+\frac {0.448(1-0.448)}{58}}=0.1666\)

3) \(\hat {p_1}-\hat {p_2} \pm E = (0.758,-0.448) \pm 0.1666\)

The 95% confidence interval about the difference of the proportions is (0.143, 0.477). The confidence interval contains all positive values, telling you that there is a significant difference between the proportions AND the first group (BMPs used with management plans) is significantly greater than the second group (BMPs with no plans). This confidence interval estimates the difference in proportions. For this problem, we can say that correctly implemented BMPs with a plan occur in a greater proportion (14.3% to 44.7%) compared to those implemented without a management plan.

Software Solutions

Minitab

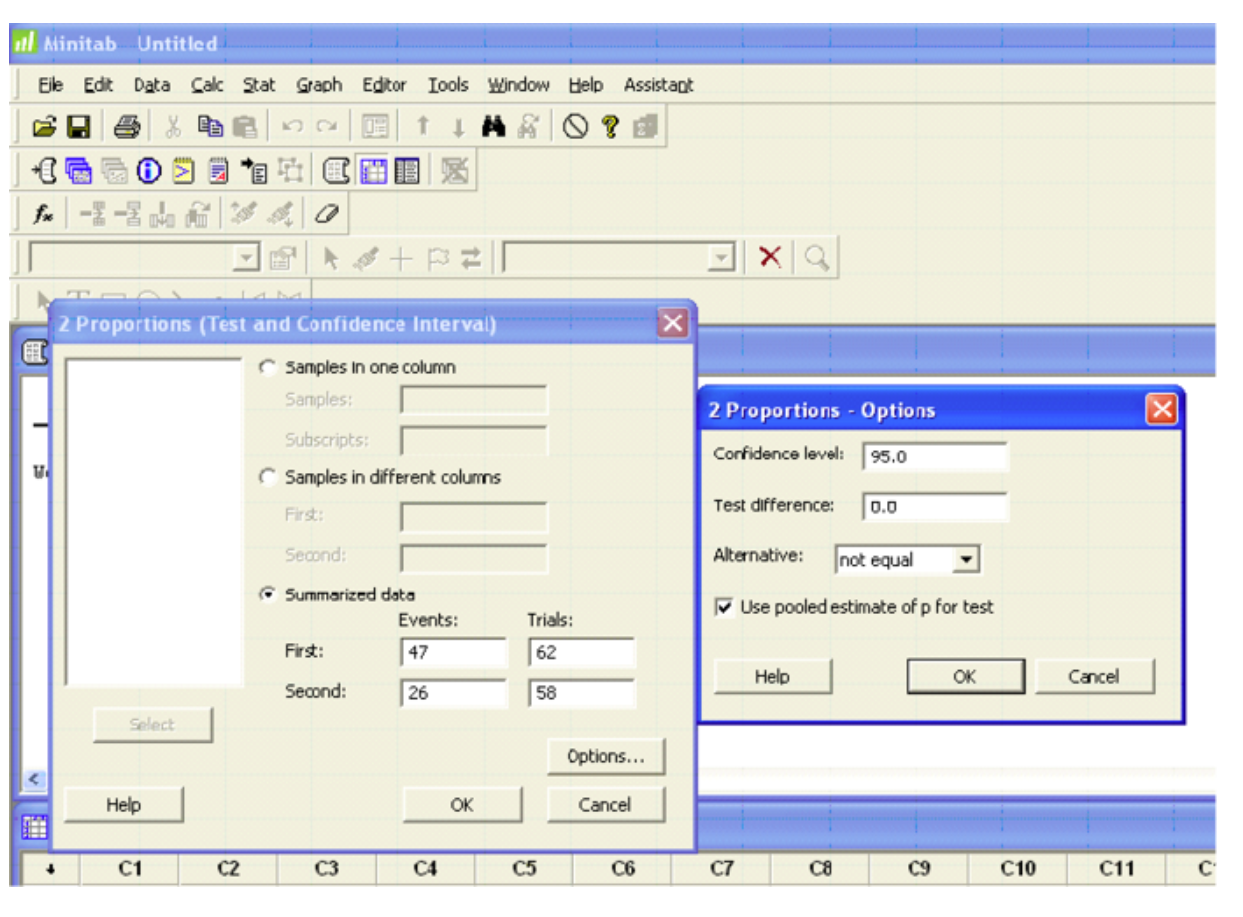
Test and CI for Two Proportions

Sample	X	N	Sample p
1	47	62	0.758065
2	26	58	0.448276
Difference = p (1) – p (2)
Estimate for difference: 0.309789
95% CI for difference: (0.143223, 0.476355)
Test for difference = 0 (vs. not = 0): Z = 3.47 p-value = 0.001
Fisher’s exact test: p-value = 0.001

The p-value equals 0.001 which tells us to reject the null hypothesis. There is a significant difference in the proportion of correctly implemented BMPs with and without management plans. The confidence interval for the difference in proportions is also given (0.143223, 0.476355) which allows us to estimate the difference.

Excel

Excel does not analyze data from proportions.