17.5: Testing regression coefficients
- Page ID
- 45253
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Introduction
Whether the goal is to create a predictive model or an explanatory model, then there are two related questions the analyst asks about the linear regression model fitted to the data:
- Does a line actually fit the data
- Is the linear regression statistically significant?
We will turn to the first question pertaining to fit in time, but for now, focus on the second question.
Like the one-way ANOVA, we have the null and alternate hypothesis for the regression model itself. We write our hypotheses for the regression:
\(H_{O}\): linear regression fits the data vs. \(H_{A}\): linear regression does not fit
We see from the output in R and Rcmdr that an ANOVA table has been provided. Thus, the test of the regression is analogous to an ANOVA — we partition the overall variability in the response variable into two parts: the first part is the part of the variation that can be explained by there being a linear regression (the linear regression sum of squares) plus a second part that accounts for the rest of the variation in the data that is not explained by the regression (the residual or error sum of squares). Thus, we have \[SS_{total} = SS_{regression} + SS_{residual} \nonumber\]
As we did in ANOVA, we calculate Mean Squares \(MS_{x} = SS_{x} / DF_{x}\), where \(x\) refers to either “regression” or “residual” sums of squares and degrees of freedom. We then calculate \(F\)-values, the test statistics for the regression, to test the null hypothesis.
The degrees of freedom (DF) in simple linear regression are always \[\begin{align*} & DF_{total} = n - 1 \\ & DF_{regresion} = 1 \\ & DF_{residual} = DF_{total} - DF_{regression} = n - 2 \end{align*}\]
where \[F = \frac{MS_{regression}}{MS_{residual}} \nonumber\]
and \(F_{DF \ regression}\), \(DF_{residual}\) are compared to the critical value at Type I error rate \(\alpha\), with \(DF_{regression}\), \(DF_{residual}\).
Linear regression inference
Estimation of the slope and intercept is a first step and should be accompanied by the calculation of confidence intervals.
What we need to know if we are to conclude that there’s a functional relationship between the \(X\) and \(Y\) variable is whether the same relationship exists in the population. We’ve sampled from the population, calculated an equation to describe the relationship between them. However, just as in all cases of inferential statistics, we need to consider the possibility that, through chance alone, we may have committed a Type I error.
The graph below (Fig. \(\PageIndex{1}\)) shows a possible outcome under a scenario in which the statistical analyst would likely conclude that there is a statistically significant linear model fit to the data, but the true relationship in the population was a slope of zero. How can this happen? Under this scenario, by chance alone the researchers sampled points (circled in red) from the population that fall along a line. We will conclude that there is linear relationship — that’s what are inferential statistics work would indicate — but there was none in the population from which the sampling was done; there would be no way for us to recognize the error except to repeat the experiment — the principal of research reproducibility — with a different sample.

So in conclusion, you must keep in mind the meaning of statistical significance in the context of statistical inference: it is inference done on a background of random chance, the chance that sampling from the population leads to a biased sample of subjects.
If you think about what I did with this data for the Figure \(\PageIndex{1}\) graph, purposely selecting data that showed a linear relationship between Y and X (red circles), then you should recognize this as an example of data dredging or p-hacking, cf. discussion in Head et al (2015); Stefan and Schönbrodt (2023). However, the graph is supposed to be read as if we could do a census and therefore have full knowledge of the true relationship between \(y\) and \(x\). The red circles indicate the chance that sampling from a population may sometimes yield incorrect conclusions.
Tests of coefficients
One criterion for a good model is that the coefficients in the model, the intercept and the slope(s) are all statistically significant.
For the statistical of the slope, \(b_{1}\), we generally treat the test as a two-tailed test of the null hypothesis that the regression slope is equal to zero.
\(H_{O}: b_{1} = 0\) vs. \(H_{A}: b_{1} \neq 0\)
Similarly, for the statistical of the intercept, \(b_{0}\), we generally treat the test as a two-tailed test of the null hypothesis that the Y-intercept is equal to zero.
\(H_{O}: b_{0} = 0\) vs. \(H_{A}: b_{0} \neq 0\)
For both slope and intercept we use \(t\)-statistics. \[t = \frac{b}{SE_{b}} \nonumber\]
We’ll illustrate the tests of the slope and intercept by letting R and Rcmdr do the work. You’ll find this simple data set at the bottom of this page (scroll or click here). The first variable is the number of matings, the second is the size of the paired female, and the third is the size of the paired male. All body mass are in grams.
R code
After loading the worksheet into R and Rcmdr, begin by selecting
Rcmdr: Statistics → Fit model → Linear Regression
Note that more than one predictor can be entered, but only one response (dependent) variable may be selected (Fig. \(\PageIndex{2}\).
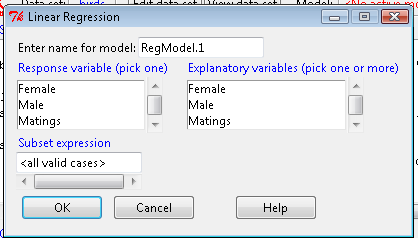
This procedure will handle simple and multiple regression problems. But before we go further, answer these two questions for the data set.
Question 1. What is the Response variable?
Question 2. What is the Explanatory variable?
Answers. See below in the R output to see if you were correct!
If there is only one predictor, then this is a Simple Linear Regression; if more than one predictor is entered, then this is a Multiple Linear Regression. We’ll get some more detail, but for now, identify the test of the slope (labeled after the name of the predictor variable), the test of the intercept, and some new stuff.
R output
RegModel.1 <- lm=(Matings ~ Female, data=birds)
summary(RegModel.1)
Call: lm(formula = Matings ~ Female, data = birds)
Residuals:
Min 1Q Median 3Q Max
-2.32805 -1.59407 -0.04359 1.77292 2.67195
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -8.6175 3.5323 -2.440 0.02528 *
Female 0.3670 0.1042 3.524 0.00243 **
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 1.774 on 18 degrees of freedom
Multiple R-squared: 0.4082, Adjusted R-squared: 0.3753 F-statistic: 12.42 on 1 and 18 DF, p-value: 0.002427
In this example, slope = 0.367 and the intercept = -8.618. The first new term we encounter is called “R-squared” \((R^{2})\) — it’s also called the coefficient of determination. It’s the ratio of the sum of squares due to the regression to the total sums of squares. \(R^{2}\) ranges from zero to 1, with a value of 1 indicating a perfect fit of the regression to the data.
If you are looking for a link between correlation and simple linear regression, then here it is: \(R^{2}\) is the square of the product-moment correlation, \(r\) (see also Chapter 17.2). Thus, \(r = \sqrt{R^{2}}\).
Interpretation of \(R^{2}\) goes like this: If \(R^{2}\) is close to zero, then the regression model does not explain much of the variation in the dependent variable; conversely, if \(R^{2}\) is close to one, then the regression model explains a lot of the variation in the dependent variable.
Did you get the Answers?
Answer 1: Number of matings
Answer 2: Size of females
Interpreting the output
Recall that \(SS_{total} = SS_{regression} + SS_{residual}\)
then \(R_{2} = SS_{regression} SS_{total}\)
From the output we see that \(R^{2}\) was 0.408, which means that about 40% of the variation in numbers of matings may be explained by size of the females alone.
To complete the analysis get the ANOVA table for the regression.
Rcmdr: Models → Hypothesis tests → ANOVA table…
> Anova(RegModel.1, type="II")
Anova Table (Type II tests)
Sum Sq Df F value Pr(>F)
Female 39.084 1 12.415 0.002427 **
Residuals 56.666 18
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
With only one predictor (explanatory) variable, note that the regression test in the ANOVA is the same (has the same probability vs. the null hypothesis) as the test of the slope.
Test two slopes
A more general test of the null hypothesis involving the slope might be
\(H_{O}: b_{1} = b\) vs. \(H_{A}: b_{1} \neq b\)
where \(b\) can be any value, including zero. Again, the \(t\)-test would then be used to conduct the test of the slope, where the \(t\)-test would have the form \[t = \frac{b_{1} - b_{2}}{SE_{b_{1} - b_{2}}} \nonumber\]
where \(SE_{b_{1} - b_{2}}\) is the standard error of the difference between the two regression coefficients. We saw something similar to this value back when we did a paired \(t\)-test. To obtain \(SE_{b_{1} - b_{2}}\), we need the pooled residual mean square and the squared sums of the \(X\) values for each of our sample.
First, the pooled (hence the subscript \(p\)) residual mean square is calculated as \[\left(s_{y \cdot x}^{2}\right)_{p} = \frac{resSS_{1}}{resDF_{1}} + \frac{resSS_{2}}{resDF_{2}} \nonumber\]
where \(resSS\) and \(resDF\) refer to residual sums of squares and residual degrees of freedom for the first (1) and second (2) regression equations.
Second, the standard error of the difference between regression coefficients (squared!!) is calculated as \[s_{b_{1} - b_{2}} = \frac{\left(s_{y \cdot x}^{2}\right)_{p}}{\sum x_{1}^{1}} + \frac{\left(s_{y \cdot x}^{2}\right)_{p}}{\sum x_{2}^{2}} \nonumber\]
where the subscript “1” and “2” refer to the \(X\) values from the first sample (e.g., the body size values for the males) and the second sample (e.g., the body size values for the females).
To obtain the squared sum in R and Rcmdr, use the Calc function (e.g., to sum the squared X values for the females, use SUM(‘Female’*’Female’)).
We can then use our \(t\)-test, with the degrees of freedom now \[DF = n_{1} + n_{2} - 4 \nonumber\]
Alternatively, the \(t\)-test of two slopes can be written as \[t = \frac{b_{1} - b_{2}}{\left(SE_{b_{1}}^{2} + SE_{b_{2}}^{2}\right)^{2} \nonumber\]
with again \(DF = n_{1} + n_{2} - 4\).
In this way, we can see a way to test any two slopes for equality. This would be useful if we wanted to compare two samples (e.g., males and females) and wanted to see if the regressions were the same (e.g., metabolic rate covaried with body mass in the same way — that is, the slope of the relationship was the same). This situation arises frequently in biology. For example, we might want to know if male and female birds have different mean field metabolic rates, in which case we might be tempted to use a one-way ANOVA or \(t\)-test (since there is one factor with two levels). However, if males and females also differ for body size, then any differences we might see in metabolic rate could be due to differences in metabolic rate or to differences in the covariable of body size. The test is generally referred to as the analysis of covariance (ANCOVA), which is the subject of Chapter 17.6. In brief, ANCOVA allows you to test for mean differences in traits like metabolic rate between two or more groups, but after first accounting for covariation due to another variable (e.g., body size). However, ANCOVA makes the assumption that the relationship between the covariable and the response variable is the same in the two groups. This is the same as saying that the regression slopes are the same. Let’s proceed to see how we can compare regression slopes, then move to a more general treatment in Chapter 17.6.
Example
For a sample of 13 tadpoles (Rana pipiens), hatched in the laboratory.
M. Dohm unpublished results from my undergraduate days, You’ll find this simple data set at the bottom of this page (scroll or click here).
You should confirm your self, but the slope of the regression equation of oxygen consumption (ml O2/hour) on body mass (g) was 444.95 (with SE = 65.89). Plot of data shown in Figure \(\PageIndex{3}\).
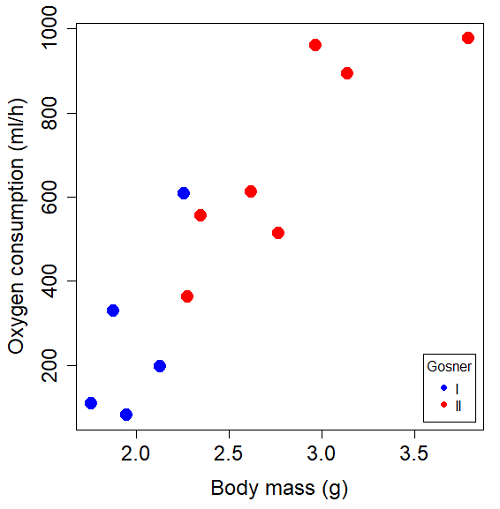
The project looked at whether metabolism as measured by oxygen consumption was consistent across two developmental stages. Metamorphosis in frogs and other amphibians represents profound reorganization of the organism as the tadpole moves from water to air. Thus, we would predict some cost as evidenced by change in metabolism associated with later stages of development. Figure \(\PageIndex{4}\) shows a box plot of tadpole oxygen consumption by Gosner (1960) developmental stage.
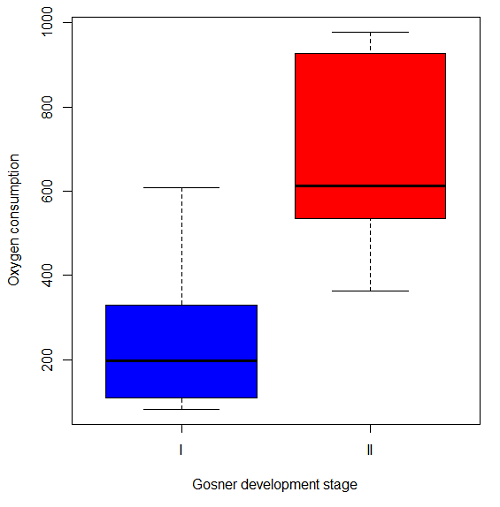
Looking at Figure \(\PageIndex{4}\) we see a trend consistent with our prediction; developmental stage may be associated with increased metabolism. However, older tadpoles also tend to be larger, and the plot in Figure \(\PageIndex{4}\) does not account for that. Thus, body mass is a confounding variable in this example. There are several options for analysis here (e.g., ANCOVA), but one way to view this is to compare the slopes for the two developmental stages. While this test does not compare the means, it does ask a related question: is there evidence of change in rate of oxygen consumption relative to body size between the two developmental stages? The assumption that the slopes are equal is a necessary step for conducting the ANCOVA, which we describe in Chapter 17.6.
So, divide the data set into two groups by developmental stage (12 tadpoles could be assigned to one of two developmental stages; one was at a lower Gosner stage than the others and so is dropped from the subset.
Gosner stage I:
| Body mass | VO2 |
| 1.76 | 109.41 |
| 1.88 | 329.06 |
| 1.95 | 82.35 |
| 2.13 | 198 |
| 2.26 | 607.7 |
Gosner stage II:
| Body mass | VO2 |
| 2.28 | 362.71 |
| 2.35 | 556.6 |
| 2.62 | 612.93 |
| 2.77 | 514.02 |
| 2.97 | 961.01 |
| 3.14 | 892.41 |
| 3.79 | 976.97 |
The slopes and standard errors were
| Gosner Stage I | Gosner stage II | |
| slope | 750.0 | 399.9 |
| standard error of slope | 444.6 | 111.2 |
Rcmdr: Models – Compare model coefficients..
compareCoefs(gosI.1, gosII.1)
Calls:
1: lm(formula = VO2 ~ Body.mass, data = gosI)
2: lm(formula = VO2 ~ Body.mass, data = gosII)
Model 1 Model 2
(Intercept) -1232 -441
SE 891 321
Body.mass 750 400
SE 445 111
Are the two slopes equal?
Looking at the table, we would say No, because the slopes look different (750 vs 399.9). However, the errors are large and, given this is a small data set, we need to test statistically; are the slopes indistinguishable \(\left(H_{O}: b_{I} = b_{II}\right)\), where \(b_{I}\) is the slope for the Gosner Stage I subset and \(b_{II}\) is the slope for the Gosner Stage II subset?
To use our tests discussed above, we need the sum of squared \(X\) values for Gosner Stage I and sum of squared \(X\) values for Gosner stage II results. We can get these from the ANOVA tables. Recall that we can apply:
ANOVA regression Gosner Stage I
Anova(gosI.1, type="II")
Anova Table (Type II tests)
Response: VO2
Sum Sq Df F value Pr(>F)
Body.mass 89385 1 2.8461 0.1902
Residuals 94220 3
ANOVA regression Gosner Stage II
Anova(gosII.1, type="II")
Anova Table (Type II tests)
Response: VO2
Sum Sq Df F value Pr(>F)
Body.mass 258398 1 12.935 0.0156 *
Residuals 99882 5
SSgosnerI = 89385
SSgosnerII = 258398
We also need the residual Mean Squares (SSresidual/DFresidual) from the ANOVA tables
MSgosnerI = 94220/3 = 31406.67
MSgosnerII = 99882/5 = 19976.4
Therefore, the pooled residual MS is \(\left(s_{x \cdot y}^{2}\right)_{p} = 51383.07\) and the pooled SE of the difference is \(s_{b_{1} - b_{2}} = 3440.359\) using the formulas above.
Now, we plug in the values to get a \(t\)-test: \(t = \dfrac{750 - 444.6}{3440.359} = 0.0887698\).
The DF for this t-test are \(n_{1} + n_{2} - 4 = 4 + 6 - 4 = 6\).
Using Table of Student’s \(t\) distribution (Appendix), I find the two-tailed critical value for \(t\) at alpha = 5% with DF = 6 is equal to 3.758. Since \(0.0887698 << 3.758\), we cannot conclude that the two slopes are statistically different.
Questions
Metabolic rates like oxygen consumption over time are well-known examples of allometric relationships. That is, many biological variables (e.g., \(\dot{V} O_{2}\) is related as \(a \cdot M^{b}\), where \(M\) is body mass, \(b\) is scaling exponent (the slope!), and \(a\) is a constant (the intercept!)) are best evaluated on log-log scale. Redo the linear regression of oxygen consumption vs. body mass for the tadpoles, but this time, apply log10-transform to VO2 and to Body.mass.
Data in this page, bird matings
| Body mass | Matings |
| 29 | 0 |
| 29 | 2 |
| 29 | 4 |
| 32 | 4 |
| 32 | 2 |
| 35 | 6 |
| 36 | 3 |
| 38 | 3 |
| 38 | 5 |
| 38 | 8 |
| 40 | 6 |
Data in this page, Oxygen consumption, \(\dot{V} O_{2}\), of Anuran tadpoles
| Gosner | Body mass | VO2 |
| NA | 1.46 | 170.91 |
| I | 1.76 | 109.41 |
| I | 1.88 | 329.06 |
| I | 1.95 | 82.35 |
| I | 2.13 | 198 |
| II | 2.28 | 362.71 |
| I | 2.26 | 607.7 |
| II | 2.35 | 556.6 |
| II | 2.62 | 612.93 |
| II | 2.77 | 514.02 |
| II | 2.97 | 961.01 |
| II | 3.14 | 892.41 |
| II | 3.79 | 976.97 |
Gosner refers to Gosner (1960), who developed a criteria for judging metamorphosis staging.


