17.1: Simple linear regression

Introduction

Linear regression is a toolkit for developing linear models of cause and effect between a ratio scale data type, response or dependent variable, often labeled \(Y\), and one or more ratio scale data type, predictor or independent variables, \(X\). Like ANOVA, linear regression is a special case of the general linear model. Regression and correlation both test linear hypotheses: we state that the relationship between two variables is linear (the alternate hypothesis) or it is not (the null hypothesis). The difference?

• Correlation is a test of association (are variables correlated, we ask?), but are not tests of causation: we do not imply that one variable causes another to vary, even if the correlation between the two variables is large and positive, for example. Correlations are used in statistics on data sets not collected from explicit experimental designs incorporated to test specific hypotheses of cause and effect.
• Linear regression is to cause and effect as correlation is to association. With regression and ANOVA, which again, are special cases of the general linear model (LM), we are indeed making a case for a particular understanding of the cause of variation in a response variable: modeling cause and effect is the goal.

We start our LM model as \(Y \sim model\) where “\(\sim\)”, tilda, is an operator used by R in formulas to define the relationship between the response variable and the predictor variable(s).

From R Commander we call the linear model function by Statistics → Fit models → Linear model … , which brings up a menu with several options (Fig. 1).

Figure \(\PageIndex{1}\): R commander menu interface for linear model.

Our model was

Matings ~ Body.Mass

R commander will keep track of the models created and enter a name for the object. You can, and probably should, change the object name yourself. The example shown in Figure \(\PageIndex{1}\) is a simple linear regression, with Body.Mass as the Y variable and Matings the X variable. No other information need be entered and one would simply click OK to begin the analysis.

Example

The purpose of regression is similar to ANOVA. We want a model, a statistical representation to explain the data sample. The model is used to show what causes variation in a response (dependent) variable using one or more predictors (independent variables). In life history theory, mating success is an important trait or characteristic that varies among individuals in a population. For example we may be interested in determining the effect of age \(\left(X_{1}\right)\) and body size \(\left(X_{2}\right)\) on mating success for a bird species. We could handle the analysis with ANOVA, but we would lose some information. In a clinical trial, we may predict that increasing Age \(\left(X_{1}\right)\) and BMI \(\left(X_{1}\right)\) causes increase blood pressure \((Y)\).

Our causal model looks like \(X_{1} + X_{2} \rightarrow Y\).

Let’s review the case for ANOVA first.

The response (dependent variable), the number of successful matings for each individual, would be a quantitative (interval scale) variable. (Reminder: You should be able to tell me what kind of analysis you would be doing if the dependent variable was categorical!) If we use ANOVA, then factors have levels. For example, we could have several adult birds differing in age (factor 1) and of different body sizes. Age and body size are quantitative traits, so, in order to use our standard ANOVA, we would have to assign individuals to a few levels. We could group individuals by age (e.g., < 6 months, 6 – 10 months, > 12 months) and for body size (e.g., small, medium, large). For the second example, we might group the subjects into age classes (20-30, 30-40, etc), and by AMA recommended BMI levels (underweight < 18.5, normal weight 18.5 – 24.9, overweight 25-29.9, obese > 30).

We have not done anything wrong by doing so, but if you are a bit uneasy by this, then your intuition will be rewarded later when we point out that in most cases you are best to leave it as a quantitative trait. We proceed with the test of ANOVA, but we are aware that we’ve lost some information — continuous variables (age, body size, BMI) were converted to categories — and so we suspect (correctly) that we’ve lost some power to reject the null hypothesis. By the way, when you have a “factor” that is a continuous variable, we call it a “covariate.” Factor typically refers to a categorical explanatory (independent) variable.

We might be tempted to use correlation — at least to test if there’s a relationship between Body Mass and Number of Matings. Correlation analysis is used to measure the intensity of association between a pair of variables. Correlation is also used to to test whether the association is greater than that expected by chance alone. We do not express one as causing variation in the other variable, but instead, we ask if the two variables are related (covary). We’ve already talked about some properties of correlation: it ranges from \(-1\) to \(+1\) and the null hypothesis is that the true association between two variables is equal to zero. We will formalize the correlation next time to complete our discussion of the linear relationship between two variables.

But regression is appropriate here because we are indeed making a causal claim: we selected Age and Body Size, and we selected Age and BMI in the second example wish to develop a model so we can predict and maybe even advise.

Least squares regression explained

Regression is part of the general linear model family of tests. If there is one linear predictor variable, then that is a simple linear regression (SLR), also called ordinary least squares (OLS), if there are two or more linear predictor variables, then that is a multiple linear regression (MLR, Chapter 18).

First, consider one predictor variable. We begin by looking at how we might summarize the data by fitting a line to the data; we see that there’s a relationship between mass and mating success in both young and old females (and maybe in older males).

The data set was

Table \(\PageIndex{1}\). Our data set of number of matings by male bird by body mass (g).

ID	Body.Mass	Matings
1	29	0
2	29	2
3	29	4
4	32	4
5	32	2
6	35	6
7	36	3
8	38	3
9	38	5
10	38	8
11	40	6

And a scatterplot of the data (Fig. \(\PageIndex{2}\))

Figure \(\PageIndex{2}\): Number of matings by body mass (g) of the male bird.

There’s some scatter, but our eyes tell us that as body size increases, the number of matings also increases. We can go so far as to say that we can predict (imperfectly) that larger birds will have more matings. We fit the best-fit line to the data and added the line to our scatterplot (Fig. \(\PageIndex{3}\)). The best-fit line meets the requirements that the error about the line is minimized (see below). Thus, we would predict about six matings for a 40-gram bird, but only two matings for a 28-gram bird. And this is a good feature of regression, prediction, as long as used with some caution.

Figure \(\PageIndex{3}\): Same data as in Fig. \(\PageIndex{2}\), but with the “best fit” line.

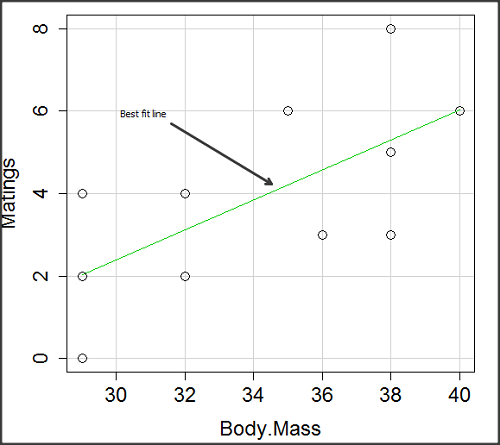
Note that prediction works best for the range of data for which the regression model was built. Outside the range of values, we predict with caution.

The simplest linear relationship between two variables is the SLR. This would be the parameter version (population, not samples), where \(Y_{i} = \alpha + \beta X_{i} + \epsilon_{i}\)

\(\alpha\) = the Y-intercept coefficient and it is defined as \(a = \bar{Y} - b \bar{X}\). Solve for intercept by setting \(X = 0\).

\(\beta\) = the regression coefficient (slope)

\(\beta\) = \dfrac{\sum \left(X_{i} - \bar{X}\right) \cdot \left(Y_{i} - \bar{Y}\right)}{\sum \left(X_{i} - \bar{X}\right)^{2}}\)

Note that the denominator is just our corrected sums of squares that we’ve seen many times before. The numerator is the cross-product and is referred to as the covariance.

\(\epsilon\) = the error or “residual”, \(\epsilon_{i} = Y_{i} - \hat{Y}_{i}\)

The residual is an important concept in regression. We briefly discussed “what’s left over,” in ANOVA, where an observation \(Y_{i}\) is equal to the population mean plus the factor effect of level \(i\) plus the remainder or “error”.

In regression, we speak of residuals as the departure (difference) of an actual \(Y_{i}\) (observation) from the predicted \(Y\) (\(\hat{Y}\), say “Y-hat”).

The linear regression predicts \(Y\), and what remains unexplained by the regression equation is called the residual. There will be as many residuals as there were observations.

But why THIS particular line? We could draw lines anywhere through the points. Well, this line is termed the “best fit“ because it is the only line that minimizes the sum of the squared deviations for all values of \(Y\) (the observations) and the predicted \(\hat{Y}\). The best fit line minimizes the sum of the squared residuals, \(\displaystyle \sum_{i=1}^{n} \left(Y_{i} - \hat{Y}_{i}\right)^{2}\).

Thus, like ANOVA, we can account for the total sums of squares \(\left(SS_{tot}\right)\) as equal to the sums of squares (variation), explained by the regression model, \(\left(SS_{reg}\right)\), plus what’s not explained, what’s left over, the residual sums of squares, \(\left(SS_{res}\right)\), aka \(\left(SS_{error}\right)\).

\[SS_{tot} = SS_{reg} + SS_{res} \nonumber\]

Models used to predict new values

Once a line has been estimated, one use is to predict new observations not previously measured!

Figure \(\PageIndex{4}\): Figure \(\PageIndex{3}\) redrawn to extend the line to the \(Y\)-intercept.

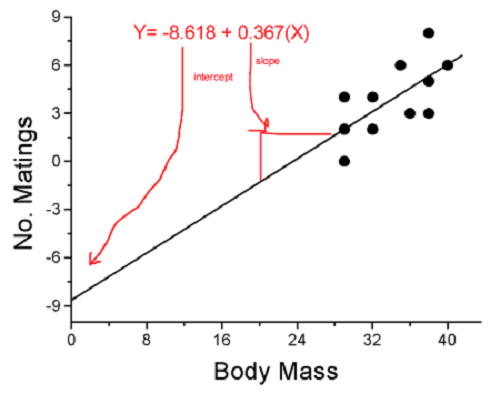
This is an important use of models in statistics: use an equation to fit to some data, then predict \(Y\) values from new values of \(X\). To use the equation, simply insert new values of \(X\) into the equation, because the slope and intercept are already “known.” Then for any \(X_{i}\) we can determine \(\hat{Y}\) (predicted \(Y\) value that is on the best-fit regression line).

This is what people do when they say

“if you are a certain weight (or BMI) you have this increased risk of heart disease”

“if you have this number of black rats in the forest you will have this many nestlings survive to leave the nest”

“if you have this much run-off pollution into the ocean you have this many corals dying”

“if you add this much enzyme to the solution you will have this much resulting product”.

R Code

We can use the drop down menu in Rcmdr to do the bulk of the work, supplemented with a little R code entered and run from the script window. Scrape data from Table \(\PageIndex{1}\) and save to R as bird.matings.

LinearModel.3 <- lm(Matings ~ Body.Mass, data=bird.matings)
summary(LinearModel.3)

Output from R:

Call:
lm(formula = Matings ~ Body.Mass, data = bird.matings)

Residuals:
     Min       1Q   Median      3Q     Max 
-2.29237 -1.34322 -0.03178 1.33792 2.70763

Coefficients:
            Estimate Std. Error  t value  Pr(>|t|) 
(Intercept)  -8.4746     4.6641   -1.817    0.1026 
Body.Mass     0.3623     0.1355    2.673    0.0255 *
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 1.776 on 9 degrees of freedom
Multiple R-squared: 0.4425, Adjusted R-squared: 0.3806 
F-statistic: 7.144 on 1 and 9 DF, p-value: 0.02551

Get the sum of squares from the ANOVA table

myAOV.full <- anova(LinearModel.3); myAOV.full

Output from R, the ANOVA table

Analysis of Variance Table

Response: Matings
           Df  Sum Sq  Mean Sq  F value     Pr(>F)
Body.Mass   1  22.528  22.5277   7.1438   0.02551 *
Residuals   9  28.381   3.1535
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

We can do more,

str(myAOV.full)

Note:

str() command lets us look at an object created in R. Type ?str or help(str) to bring up the R documentation. Here, we use str() to look at the structure of the object we created, myAOV.full. “Classes” refers to the R programming class attribute inherited by the object.

Output from R:

Classes 'anova' and 'data.frame': 2 obs. of 5 variables:
$ Df : int 1 9
$ Sum Sq : num 22.5 28.4
$ Mean Sq: num 22.53 3.15
$ F value: num 7.14 NA
$ Pr(>F) : num 0.0255 NA
- attr(*, "heading")= chr [1:2] "Analysis of Variance Table\n" "Response: Matings"

Extract the sum of squares: type the object name then $"Sum Sq" at the R prompt.

myAOV.full $"Sum Sq"

Output from R:

[1] 22.52773 28.38136

Get the residual sum of squares.

SSE.myAOV.full <- myAOV.full $"Sum Sq"[2]; SSE.myAOV.full

Output from R:

[1] 22.52773

Get the regression sum of squares.

SSR.myAOV.full <- myAOV.full $"Sum Sq"[1]; SSR.myAOV.full

Output from R:

[1] 50.90909

Now, get the total sums of squares for the model.

ssTotal.myAOV.full <- SSE.myAOV.full + SSR.myAOV.full; ssTotal.myAOV.full

Calculate the coefficient of determination.

myR_2 <- 1 - (SSE.myAOV.full/(ssTotal.myAOV.full)); myR_2

Output from R:

[1] 0.4425091

Which matches what we got before, as it should.

Regression equations may be useful to predict new observations

True. However, you should avoid making estimates beyond the range of the \(X\)-values that were used to calculate the best-fit regression equation! Why? The answer has to do with the shape of the confidence interval around the regression line.

I’ve drawn an exaggerated confidence interval (CI), for a regression line between an \(X\) and a \(Y\) variable. Note that the \(CI\) is narrow in the middle, but wider at the end. Thus, we have more confidence in predicting new \(Y\) values for data that fall within the original data because this is the region where we are most confident.

Calculating the \(CI\) for the linear model follows from \(CI\) calculations for other estimates. It is a simple concept — both the intercept and slope were estimated with error, so we combine these into a way to generalize our confidence in the regression model as a whole given the error in slope and intercept estimation. \[95\% \ CI = b_{1} \pm t_{df} SE_{b1} \nonumber\]

The calculation of confidence interval for the linear regression involves the standard error of the residuals, the sample size, and expressions relating the standard deviation of the predictor variable \(X\) — we use the \(t\)-distribution.

Figure \(\PageIndex{5}\): 95% confidence interval about the best fit line.

How I got this graph

plot(bird_matings$Body.Mass,bird_matings$Mating,xlim=c(25,45),ylim=c(0,10))
mylm <- lm(bird_matings$Mating~bird_matings$Body.Mass)
predict(mylm, interval = c("confidence"))
abline(mylm, col = "black")
x<-bird_matings$Body.Mass
lines(x, prd[,2], col= "red", lty=2)
lines(x, prd[,3], col= "red", lty=2)

Nothing wrong with my code, but getting all of this to work in R might best be accomplished by adding another package, a plug-in for Rcmdr called RcmdrPlugin.HH. HH refers to Heiberger and Holland, who designed this package specializing in graphical displays of data and data analysis.

Assumptions of OLS, introduction

We will cover assumptions of OLS in detail in 17.8, Assumptions and model diagnostics for Simple Linear Regression. For now, briefly, the assumptions for OLS regression include:

1. Linear model is appropriate: the data are well described (fit) by a linear model
2. Independent values of \(Y\) and equal variances. Although there can be more than one \(Y\) for any value of \(X\), the \(Y\)’s cannot be related to each other (that’s what we mean by independent). Since we allow for multiple \(Y\)’s for each \(X\), then we assume that the variances of the range of \(Y\)’s are equal for each \(X\) value (this is similar to our ANOVA assumptions for equal variance by groups).
3. Normality. For each \(X\) value there is a normal distribution of \(Y\)’s (think of doing the experiment over and over)
4. Error (residuals) are normally distributed with a mean of zero.

Additionally, we assume that measurement of \(X\) is done without error (the equivalent, but less restrictive practical application of this assumption is that the error in \(X\) is at least negligible compared to the measurements in the dependent variable). Multiple regression makes one more assumption, about the relationship between the predictor variables (the \(X\) variables). The assumption is that there is no multicolinearity: the \(X\) variables are not related or associated to each other.

In some sense the first assumption is obvious if not trivial — of course a “line” needs to fit the data so why not plow ahead with the OLS regression method, which has desirable statistical properties and let the estimation of slopes, intercept and fit statistics guide us? One of the really good things about statistics is that you can readily test your intuition about a particular method using data simulated to meet, or not to meet, assumptions.

Coming up with datasets like these can be tricky for beginners. Thankfully others have stepped in and provide tools useful for data simulations which greatly facilitate the kinds of testing of assumptions statisticians greatly encourage us all to do (see Chatterjee and Firat 2007).

---

Questions

1. True or False. Regression analysis results in a model of the cause-effect relationship between a dependent and one (simple linear) or more (multiple) predictor variables. The equation can be used to predict new observations of the dependent variable.
2. True or False. The value of \(X\) at the \(Y\)-intercept is always equal to zero in a simple linear regression.
3. Anscombe’s quartet (Anscombe 1973) is a famous example of this approach and the fictitious data can be used to illustrate the fallacy of relying solely on fit statistics and coefficient estimates.
   
   Here are the data (modified from Anscombe 1973, p. 19) — I leave it to you to discover the message by using linear regression on Anscombe’s data set. Hint: play naïve and generate the appropriate descriptive statistics, make scatterplots for each \(X, Y\) set, then run regression statistics, first on each of the \(X, Y\) pairs (there were four sets of \(X, Y\) pairs).

   Set 1		Set 2		Set 3		Set 4
   x1	y1	x2	y2	x3	y3	x4	y4
   10	8.04	10	9.14	10	7.46	8	6.58
   8	6.95	8	8.14	8	6.77	8	5.76
   13	7.58	13	8.74	13	12.74	8	7.71
   9	8.81	9	8.77	9	7.11	8	8.84
   11	8.33	11	9.26	11	7.81	8	8.47
   14	9.96	14	8.1	14	8.84	8	7.04
   6	7.24	6	6.13	6	6.08	8	5.25
   4	4.26	4	3.1	4	5.39	19	12.5
   12	10.84	12	9.13	12	8.15	8	5.56
   7	4.82	7	7.26	7	6.42	8	7.91
   5	5.68	5	4.74	5	5.73	8	6.89