15.1: Kruskal-Wallis and ANOVA by ranks

Introduction

When the data are NOT normally distributed OR when the variances in the different samples are NOT equal, one option is to opt for a non-parametric alternative and use the Kruskal-Wallis test.

It is known that the an ANOVA on ranks of the original data will yield the same results as the original data.

Kruskal-Wallis

Rcmdr: Statistics → Nonparametric test → Kruskal-Wallis test…

Rcmdr Output of Kruskal-Wallis test

tapply(Pop_data$Stuff, Pop_data$Pop, median, na.rm=TRUE)

Pop1 Pop2 Pop3 Pop4 
 146   90  122  347 
kruskal.test(Stuff ~ Pop, data=Pop_data) 
Kruskal-Wallis rank sum test 
data: Stuff by Pop 
Kruskal-Wallis chi-squared = 25.6048, df = 3, p-value = 1.154e-05

End of R output

So, we reject the null hypothesis, right?

Compare parametric test and alternative non-parametric test

Let’s compare the nonparametric test results to those from an analysis of the ranks (ANOVA of ranks).

To get the ranks in R Commander (example.15.1 data set is available at bottom of this page; scroll down or click here).

Rcmdr: Data → Manage variables in active data set → Compute new variable …

The command for ranks is…. wait for it …. rank(). In the popup menu box, name the new variable (Ranks) and in the Expression to compute box enter rank(Values).

Figure \(\PageIndex{1}\): Screenshot of Rcmdr menu, Create New Variable.

Note:

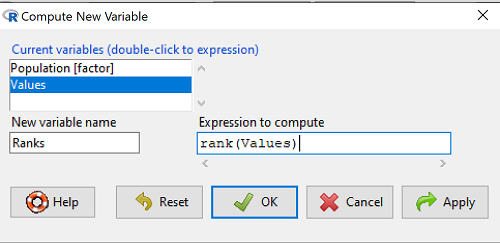
It's not a good idea to name an object Ranks, because that’s similar to a function name in R, rank.

And the R code is simply

example.15.1$Ranks <- with(example.15.1, rank(Values))

Note:

The object example.15.1$Ranks adds our new variable to our data frame.

That’s one option, to rank across the entire data set. Another option would be to rank within groups.

R code:

example.15.1$xRanks <- ave(Values, Population, FUN=rank)

Note:

The ave() function averages within subsets of the data and applies whatever summary function (FUN) you choose. In this case we used rank. Alternative approaches could use split or lapply or variations of dplyr. ave() is in the base package and at least in this case is simply to use to solve our rank within groups problem. xRanks would then be added to the existing data frame.

Here are the results of ranking within groups.

Population 1	Rank1	Population 2	Rank2	Population 3	Rank3	Population 4	Rank4
105	11.5	100	9	130	17.5	310	33
132	19	65	4	95	7	302	32
156	22	60	2.5	100	9	406	38
198	29	125	16	124	15	325	34
120	13.5	80	5.5	120	13.5	298	31
196	28	140	21	180	26	412	39.5
175	24	50	1	80	5.5	385	39.5
180	26	180	26	210	30	329	35
136	20	60	2.5	100	9	375	37
105	115	130	17.5	170	23	365	36

Question. Which do you choose, rank across groups (Ranks) or rank within groups (xRanks)? Recall that this example began with a nonparametric alternative to the one-way ANOVA, and we were testing the null hypothesis that the group means were the same.

\(H_{O}: \bar{X}_{1} = \bar{X}_{2} = \bar{X}_{3}\)

Answer. Rank the entire data set, ignoring the groups. The null hypothesis here is that there is no difference in median ranks among the groups. Ranking within groups simply shuffles observations within the group. This is basically the same thing as running Kruskal-Wallis test.

Run the one-way ANOVA, now on the Ranked variable. The ANOVA table is summarized below.

Source	DF	SS	MS	F	P†
Population	3	3495.1	1165.0	22.94	< 0.001
Error	36	1828.0	50.8
Total	39	5323.0

Note:

† The exact p-value returned by R was 0.0000000178. This level of precision is a bit suspect given that calculations of p-values are subject to bias too, like any estimate. Thus, some advocate to report p-values to three significant figures, and if less than 0.001, report as shown in this table. Occasionally, you may see P = 0.000 written in a journal article. This is a definite no-no; p-values are estimates of the probability of getting results more extreme then our results and the null hypothesis holds. It’s an estimate, not certainty; p-values cannot equal zero.

So, how do you choose between the parametric ANOVA and the non-parametric Kruskal-Wallis (ANOVA by Ranks) test? Think like a statistician — It is all about the type I error rate and potential bias of a statistical test. The purpose of statistics is to help us separate real effects from random chance differences. If we are employing the NHST approach, then we must consider our chance that we are committing either a Type I error or a Type II error, and conservative tests, e.g., tests based on comparing medians and not means, implies an increased chance of committing Type II errors.

---

Questions

1. Saying that nonparametric tests make fewer assumptions about the data should not be interpreted that they make no assumptions about the data. Thinking about our discussions about experimental design and our discussion about test assumptions, what assumptions must hold regardless of the statistical test used?
2. Go ahead and carry out the one-way ANOVA on the within group ranks (xRanks). What’s the p-value from the ANOVA?
3. One could take the position that only nonparametric alternative tests should be employed in place of parametric tests, in part because they make fewer assumptions about the data. Why is this position unwarranted?

---

Data used in this page

Dataset for Kruskal-Wallis test

Population	Values
Pop1	105
Pop1	132
Pop1	156
Pop1	198
Pop1	120
Pop1	196
Pop1	175
Pop1	180
Pop1	136
Pop1	105
Pop2	100
Pop2	65
Pop2	60
Pop2	125
Pop2	80
Pop2	140
Pop2	50
Pop2	180
Pop2	60
Pop2	130
Pop3	130
Pop3	95
Pop3	100
Pop3	124
Pop3	120
Pop3	180
Pop3	80
Pop3	210
Pop3	100
Pop3	170
Pop4	310
Pop4	302
Pop4	406
Pop4	325
Pop4	298
Pop4	412
Pop4	385
Pop4	329
Pop4	375
Pop4	365

Simulated values from three populations