Skip to main content
Statistics LibreTexts

9.4: Using Technology - Equal Slopes Model

  1. Last updated
  2. Save as PDF
  • Page ID
    33169

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    Using Technology

    SAS Example

    Using our Salary example using the data in the table below, we can run through the steps for the ANCOVA.

    Females Males
    Salary Years Salary Years
    80 5 78 3
    50 3 43 1
    30 2 103 5
    20 1 48 2
    60 4 80 4
    Steps in SAS
    Step 1: Are all regression slopes = 0?

    A simple linear regression can be run for each treatment group, Males and Females.

    Running these procedures using statistical software we get the following:

    Males

    Use the following SAS code:

    data equal_slopes;
input gender $ salary years;
datalines;
m 78 3
m 43 1
m 103 5
m 48 2
m 80 4
f 80 5
f 50 3
f 30 2
f 20 1
f 60 4
;
proc reg data=equal_slopes;
where gender='m';
model salary=years;
title 'Males';
run; quit;

    And here is the output that you get:

    The REG Procedure
    Mode1:: MODEL1
    Dependent Variable: salary
    Number of Observations Read 5
    Number of Observations Used 5
    Analysis of Variance
    Source DF Sum of Squares Mean Square F Value Pr > F
    Model 1 2310.40000 2310.40000 44.78 F" class=" ">0.0068
    Error 3 154.80000 51.60000   F" class=" ">
    Corrected Total 4 2465.20000  

    Females

    Use the following SAS code:

    data equal_slopes;
input gender $ salary years;
datalines;
m 78 3
m 43 1
m 103 5
m 48 2
m 80 4
f 80 5
f 50 3
f 30 2
f 20 1
f 60 4
;
proc reg data=equal_slopes;
where gender='f';
model salary=years;
title 'Females';
run; quit;

    And here is the output for this run:

    The REG Procedure
    Mode1:: MODEL1
    Dependent Variable: salary
    Number of Observations Read 5
    Number of Observations Used 5
    Analysis of Variance
    Source DF Sum of Squares Mean Square F Value Pr > F
    Model 1 2250.00000 2250.00000 225.00 F" class=" ">0.0006
    Error 3 30.00000 10.00000   F" class=" ">
    Corrected Total 4 2280.00000     F" class=" ">

    In both cases, the simple linear regressions are significant, so the slopes are not = 0.

    Step 2: Are the slopes equal?

    We can test for this using our statistical software.

    In SAS we now use proc mixed and include the covariate in the model.

    We will also include a "treatment × covariate" interaction term and the significance of this term answers our question. If the slopes differ significantly among treatment levels, the interaction \(p\)-value will be < 0.05.

    If the slopes differ significantly among treatment levels, the interaction p-value will be < 0.05.

    data equal_slopes;
input gender $ salary years;
datalines;
m 78 3
m 43 1
m 103 5
m 48 2
m 80 4
f 80 5
f 50 3
f 30 2
f 20 1
f 60 4
;
proc mixed data=equal_slopes;
class gender;
model salary = gender years gender*years;
run;
    Note

    In SAS, we specify the treatment in the class statement, indicating that these are categorical levels. By NOT including the covariate in the class statement, it will be treated as a continuous variable for regression in the model statement.

    The Mixed Procedure
    Type 3 Tests of Fixed Effects
    Effect Num DF Den DF F Value Pr > F
    years 1 6 148.06 F" class=" "><.0001
    gender 1 6 7.01 F" class=" ">0.0381
    years*gender 1 6 0.01 F" class=" ">0.9384

    So here we see that the slopes are equal and in a plot of the regressions, we see that the lines are parallel.

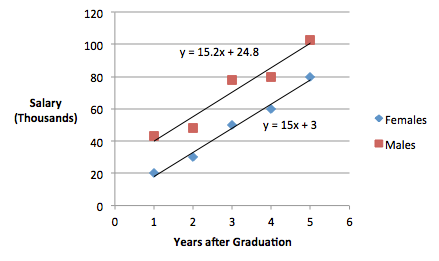
    Graph of salary in thousands vs years since graduation, separated by gender. The line of best fit for males has equation y=15.2x + 24.8, and the line of best fit for females has equation y=15x + 3.
    Figure \(\PageIndex{a1}\): Parallel lines of best fit

    To obtain the plot in SAS, we can use the following SAS code:

    SAS code:

    ods graphics on;
proc sgplot data=equal_slopes;
styleattrs datalinepatterns=(solid);
reg y=salary x=years / group=gender;
run;
    Step 3: Fit an Equal Slopes Model

    We can now proceed to fit an Equal Slopes model by removing the interaction term. Again, we will use our statistical software SAS.

    data equal_slopes;
input gender $ salary years;
datalines;
m 78 3
m 43 1
m 103 5
m 48 2
m 80 4
f 80 5
f 50 3
f 30 2
f 20 1
f 60 4
;
proc mixed data=equal_slopes;
class gender;
model salary = gender years;
lsmeans gender / pdiff adjust=tukey;
/* Tukey unnecessary with only two treatment levels */
title 'Equal Slopes Model';
run;

    We obtain the following results:

    The Mixed Procedure
    Type 3 Tests of Fixed Effects
    Effect Num DF Den DF F Value Pr > F
    years 1 7 172.55 F" class=" "><.0001
    gender 1 7 47.46 F" class=" ">0.0002
    Least Squares Means
    Effect gender Estimate Standard Error DF t Value Pr > |t|
    gender f 48.0000 2.2991 7 20.88 |t|" class=" "><.0001
    gender m 70.4000 2.2991 7 30.62 |t|" class=" "><.0001

    In SAS, the model statement automatically creates an intercept, and so the ANCOVA model is technically over-parameterized. To get the slopes and intercepts for the covariate directly, we have to re-parameterize the model. This entails suppressing the intercept ( noint ), and then specifying that we want the solutions, ( solution ), to the model. Here is what the SAS code looks like for this:

    data equal_slopes;
input gender $ salary years;
datalines;
m 78 3
m 43 1
m 103 5
m 48 2
m 80 4
f 80 5
f 50 3
f 30 2
f 20 1
f 60 4
;
proc mixed data=equal_slopes;
class gender;
model salary = gender years / noint solution;
ods select SolutionF;
title 'Equal Slopes Model';
run;

    Here is the output:

    Solution for Fixed Effects
    Effect gender Estimate Standard Error DF t Value Pr > |t|
    gender f 2.7000 4.1447 7 0.65 |t|" class=" ">0.5356
    gender m 25.1000 4.1447 7 6.06 |t|" class=" ">0.0005
    years   15.1000 1.1495 7 13.14 |t|" class=" "><.0001

    In the first section of the output above is reported a separate intercept for each gender, the ‘Estimate’ value for each gender, and a common slope for both genders, labeled ‘Years’.

    Thus, the estimated regression equation for Females is \(\hat{y} = 2.7 + 15.1(\text{Years})\), and for Males it is \(\hat{y} = 25.1 _ 15.1(\text{Years})\).

    To this point in this analysis, we can see that 'gender' is now significant. By removing the impact of the covariate, we went from

    Type 3 Tests of Fixed Effects
    Effect Num DF Den DF F Value Pr > F
    gender 1 8 2.11 F" class=" ">0.1840

    (without covariate consideration)

    to

    gender 1 7 47.46 0.0002

    (adjusting for the covariate)

    Minitab Example

    Using our Salary example and the data in the table below, we can run through the steps for the ANCOVA. On this page, we will go through the steps using Minitab.

    Females Males
    Salary Years Salary Years
    80 5 78 3
    50 3 43 1
    30 2 103 5
    20 1 48 2
    60 4 80 4
    Steps in Minitab
    Step 1: Are all regression slopes = 0?

    A simple linear regression can be run for each treatment group, Males and Females. To perform regression analysis on each gender group in Minitab, we will have to subdivide the salary data manually and separately, saving the male data into the Male Salary Dataset and the female data into the Female Salary dataset.

    Running these procedures using statistical software we get the following:

    Males

    Open the Male dataset in the Minitab project file (Male Salary Dataset).

    Then, from the menu bar, select Stat > Regression > Regression > Fit Regression Model

    In the pop-up window, select salary into Response and years into Predictors as shown below.

    Minitab popup with a response of "salary" and a continuous predictor of "years".
    Figure \(\PageIndex{b1}\): Minitab Regressions pop-up window

    Click OK, and Minitab will output the following.

    Regression Analysis: Salary versus years

    Regression Equation: salary = 24.8 + 15.2 years

    Coefficients

    Term Coef SE Coef T-Value P-Value VIF
    Constant 24.80 7.53 3.29 0.046  
    years 15.20 2.27 6.69 0.007 1.00

    Model Summary

    S R-sq R-sq (adj) R-sq (pred)
    7.18331 R-Sq = 93.7% 91.6% 85.94%

    Analysis of Variance

    Source DF SS MS F-Value P-Value
    Regression 1 2310.4 2310.40 44.78 0.007
    years 1 2310.4 2310.40 44.78 0.007
    Residual Error 3 154.8 51.6    
    Total 4 2465.2      

    Females

    Open Minitab dataset Female Salary Dataset. Follow the same procedure as was done for the Male dataset and Minitab will output the following:

    Regression Analysis: Salary versus years

    Regression Equation: salary = 3.00 + 15.00 years

    Coefficients

    Term Coef SE Coef T-Value P-Value VIF
    Constant 3.00 3.32 0.90 0.432  
    years 15.00 1.00 15.00 0.001 1.00

    Model Summary

    S R-sq R-sq (adj) R-sq (pred)
    3.16228 98.68% 98.25% 95.92%

    Analysis of Variance

    Source DF SS MS F-Value P-Value
    Regression 1 2250.0 2250.0 225.00 0.001
    years 1 2250.0 2250.0 225.00 0.001
    Residual Error 3 30.0 10.0    
    Total 4 2280.0      

    In both cases, the simple linear regressions are significant, so the slopes are not = 0.

    Step 2: Are the slopes equal?

    We can test for this using our statistical software. In Minitab, we must now use GLM (general linear model) and be sure to include the covariate in the model. We will also include a "treatment x covariate" interaction term and the significance of this term is what answers our question. If the slopes differ significantly among treatment levels, the interaction p-value will be < 0.05.

    First, open the dataset in the Minitab project file Salary Dataset. Then, from the menu select Stat > ANOVA > General Linear Model > Fit General Linear Model

    In the dialog box, select salary into Responses, gender into Factors, and years into Covariates.

    General Linear Model popup in Minitab, with "salary" selected for Responses, "gender" selected for Factors, and "years" selected for Covariates.Figure \(\PageIndex{b2}\): Minitab GLM pop-up selections

    To add the interaction term, first click Model…. Then, use the shift key to highlight gender and years, and click Add. Click OK, then OK again, and Minitab will display the following output.

    Analysis of Variance

    Source DF Adj SS Adj MS F-Value P-Value
    year 1 4560.20 4560.20 148.06 0.000
    gender 1 216.02 216.02 7.01 0.038
    years*gender 1 0.20 0.20 0.01 0.938
    Error 6 184.80 30.80    
    Total 9 5999.60      

    It is clear the interaction term is not significant. This suggests the slopes are equal. In a plot of the regressions, we can also see that the lines are parallel.

    Graph of salary in thousands vs years since graduation, separated by gender. The line of best fit for males has equation y=15.2x + 24.8, and the line of best fit for females has equation y=15x + 3.
    Figure \(\PageIndex{b3}\): Parallel lines of best fit
    Step 3: Fit an Equal Slopes Model

    We can now proceed to fit an Equal Slopes model by removing the interaction term. This can be easily accomplished by starting again with STAT > ANOVA > General Linear Model > Fit General Linear Model

    GLM model window shows the years*gender term being removed from the model.
    Figure \(\PageIndex{b4}\): Removing the years*gender term from the model

    Click OK, then OK again, and Minitab will display the following output.

    Analysis of Variance

    Source DF Adj SS Adj MS F-Value P-Value
    year 1 4560.20 4560.20 172.55 0.000
    gender 1 1254.4 1254.40 47.46 0.000
    Error 7 185.0 26.43    
    Total 9 5999.6      

    To generate the mean comparisons select STAT > ANOVA > General Linear Model > Comparisons... and fill in the dialog box as seen below.

    Comparisons window with "salary" selected as the response, "pairwise" as the type of comparison, "Tukey" as the method, and "gender" as the term for comparisons.
    Figure \(\PageIndex{b5}\): Comparisons window selections

    Click OK and Minitab will produce the following output.

    Comparison of salary

    Tukey Pairwise Comparisons: gender
    Grouping information Using the Tukey Method and 95% Confidence

    gender N Mean Grouping
    Male 5 70.4 A
    gender 5 48.0 B

    Means that do not share a letter are significantly different.

    R Example

    Steps for the ANCOVA for the Salary example in R:

    • Run a simple linear model for each treatment group.
    • Testing whether the slopes are equal.
    • Plot the regression lines.
    • Fit an equal slopes model.
    Steps in R

    1. Run a simple linear model for each treatment group (males and females) by using the following commands:

    Males

    males_regression <- lm(salary~years,data=subset(equal_slopes_data,gender=="m"))
anova(males_regression)
#Analysis of Variance Table
#Response: salary
#          Df  Sum Sq  Mean Sq  F value    Pr(>F)   
#years      1  2310.4   2310.4   44.775  0.006809 **
#Residuals  3   154.8     51.6                    
#---
#Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
#summary(males_regression)$coefficients
#              Estimate  Std. Error    t value     Pr(>|t|)
#(Intercept)       24.8    7.533923   3.291778  0.046016514
#years             15.2    2.271563   6.691427  0.006808538

    Females

    females_regression <- lm(salary~years,data=subset(equal_slopes_data,gender=="f"))
anova(females_regression)
#Analysis of Variance Table
#Response: salary
#          Df  Sum Sq  Mean Sq  F value     Pr(>F)    
#years      1    2250     2250      225  0.0006431 ***
#Residuals  3      30       10                      
#---
#Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
#  summary(females_regression)$coefficients
#              Estimate  Std. Error   t value       Pr(>|t|)
#(Intercept)          3    3.316625  0.904534   0.4323889978
#years               15    1.000000 15.000000   0.0006431193

    2. Test whether the slopes are equal by using the following commands:

    ancova_model<-lm(salary ~ gender + years + gender:years,equal_slopes_data)
anova(ancova_model)
Analysis of Variance Table
Response: salary
             Df  Sum Sq  Mean Sq  F value     Pr(>F)    
gender        1  1254.4   1254.4  40.7273  0.0006961 ***
years         1  4560.2   4560.2 148.0584  1.874e-05 ***
gender:years  1     0.2      0.2   0.0065  0.9383948    
Residuals     6   184.8     30.8                       
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

    With a p-value of 0.9383948 in the interaction term (gender*years), we can conclude that the slopes are equal.

    3. Plot the regression line for males and females by using the following commands:

    plot(years,salary, xlab="Years after graduation", ylab="Salary(Thousands)",pch=23, col=ifelse(gender=="m","red","blue"), lwd=2)
abline(males_regression)
abline(females_regression)
text(locator(1),"y=15.2x+24.8",col="red")
text(locator(1),"y=15x+3",col="blue")
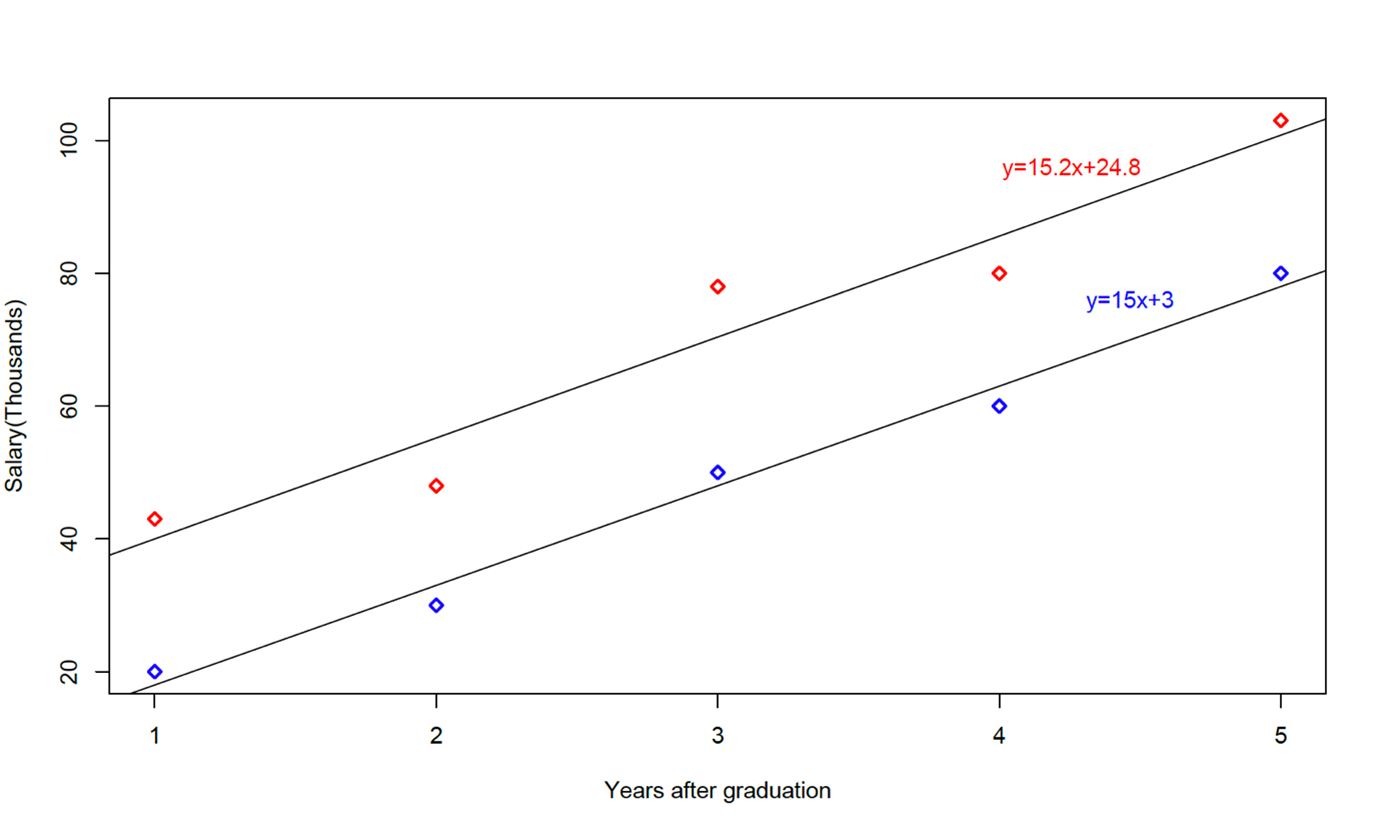
    Regression plot of salary in thousands vs years after graduation, separated by gender.
    Figure \(\PageIndex{c1}\): Regression lines for male and female data

    4. Fit an equal slopes model by using the following commands:

    equal_slopes_model<-lm(salary ~ gender + years,equal_slopes_data)
anova(equal_slopes_model)
#Analysis of Variance Table
#Response: salary
#          Df  Sum Sq  Mean Sq  F value     Pr(>F)    
#gender     1  1254.4   1254.4   47.464  0.0002335 ***
#years      1  4560.2   4560.2  172.548  3.458e-06 ***
#Residuals  7   185.0     26.4                      
#---
#Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

    We can see that gender is significant now. To estimate the two regression lines, we need the following output:

    summary(equal_slopes_model)$coefficients
#Coefficients:
#            Estimate  Std. Error  t value  Pr(>|t|)    
#(Intercept)    2.700       4.145    0.651  0.535560    
#genderm       22.400       3.251    6.889  0.000234
#years         15.100       1.150   13.136  3.46e-06
detach(equal_slopes_data)

    The estimate for the years (15.1) is the slope of the models. The intercept for females is 2.7 and the intercept for males is 2.7+22.4=25.1

    Thus, the estimated regression equation for females is \(y=15.1x + 2.7\) and for males it's \(y=15.1x + 25.1\).

    This page titled 9.4: Using Technology - Equal Slopes Model is shared under a CC BY-NC 4.0 license and was authored, remixed, and/or curated by Penn State's Department of Statistics via source content that was edited to the style and standards of the LibreTexts platform; a detailed edit history is available upon request.