14.3.1: Correlation versus Causation in Graphs
- Page ID
- 17411
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)What does the presence or the absence of a correlation between two measures mean? How should correlations be interpreted? As discussed previously, and will be discussed in more detail soon, a correlational analysis can only show the strength and direction of a linear relations. Let's use graphs to show that correlation does not equal causation.
Sometimes there's no correlation, but there is causation.
Let’s start with a case where we would expect a causal connection between two measurements. Consider, buying a snake plant for your home. Snake plants are supposed to be easy to take care of because you can mostly ignore them. But, like all plants, snake plants do need some water to stay alive. Unfortunately, they need just the right amount of water. Imagine an experiment where 1000 snake plants were grown in a house. Each snake plant is given a different amount of water per day, from zero teaspoons of water per day to 1000 teaspoons of water per day. The amount of water given each snake plant per day is one of our variables, probably the IV because it is part of the causal process that allows snake plants to grow. Every week the experimenter measures snake plant growth, which will be the second measurement. Plant growth is proably our DV, because we think that water will cause growth. Now, can you imagine for yourself what a scatter plot of weekly snake plant growth by tablespoons of water would look like?
The first plant given no water at all would have a very hard time and eventually die. It should have the least amount of weekly growth, perhaps even negative growth! How about the plants given only a few teaspoons of water per day. This could be just enough water to keep the plants alive, so they will grow a little bit but not a lot. If you are imagining a scatter plot, with each dot being a snake plant, then you should imagine some dots starting in the bottom left hand corner (no water & no plant growth), moving up and to the right (a bit of water, and a bit of growth). As we look at snake plants getting more and more water, we should see more and more plant growth, right? “Sure, but only up to a point”. Correct, there should be a trend for a positive correlation with increasing plant growth as amount of water per day increases. But, what happens when you give snake plants too much water? From Dr. Crump's personal experience, they die. So, at some point, the dots in the scatter plot will start moving back down again. Snake plants that get way too much water will not grow very well.
The imaginary scatter plot you should be envisioning could have an upside U shape. Going from left to right, the dot’s go up, they reach a maximum, then they go down again reaching a minimum. The scatter plot could look something like Figure \(\PageIndex{1}\):
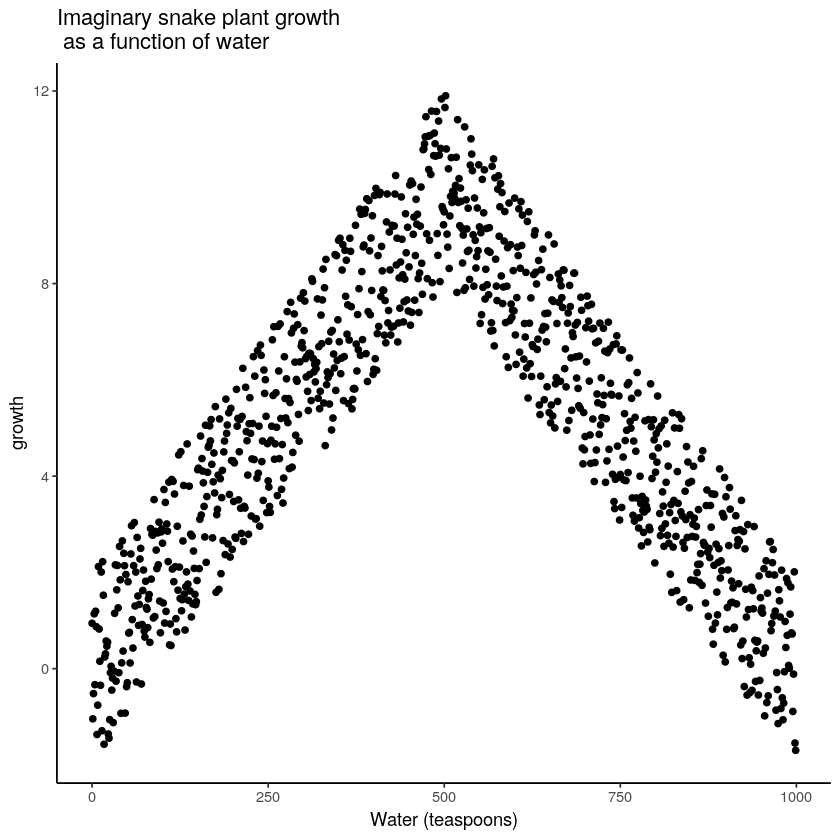
Figure \(\PageIndex{1}\): Illustration of a possible relationship between amount of water and snake plant growth. (CC-BY-SA Matthew J. C. Crump via Answering Questions with Data)
Granted this looks more like an inverted V, than an inverted U, but you get the idea right? Growth goes up with water, but eventually goes back down as too much water makes snake plants die.
Computing Pearson’s \(r\) for data like this can give you \(r\) values close to zero. Based on this statistical analysis, there is no relationship between water and growth, but the scatterplot clearly shows that there is a relations. It's just not a linear relationship (a straight line), so Pearson's \(r\) won't find it. As a result, when we compute the correlation in terms of Pearson’s r, we get a value suggesting no relationship. What this really means is there is no linear relationship (there is no relationship between the two variables that can be described by a single straight line). When we need lines or curves going in more than one direction, we have a non-linear, or cuvilinear, relationship.
This example illustrates some conundrums in interpreting correlations. We already know that water is needed for plants to grow, so we are rightly expecting there to be a relationship between our measure of amount of water and plant growth. If we look at the first half of the data we see a positive correlation (as water goes up, growth goes up), if we look at the last half of the data we see a negative correlation (as water goes up, growth goes down), and if we look at all of the data we see no correlation. Yikes. So, even when there is a causal connection between two measures, we won’t necessarily obtain clear evidence of the connection just by computing a correlation coefficient.
This is one reason why plotting your data is so important. If you see a U-shaped or reverse-U shape pattern, then a correlation analysis is probably not the best analysis for your data. There are statistical analyses that will work with these curvilinear relationships, but they are beyond the scope of an introductory statistics textbook.
Confound It: Sometimes there's a correlation, but something else causes both variables.
We discussed this "third variable" issue previously. Can you think of two quantitative variables that are related, but only because they are both caused by something else? A statistically significant correlation can occur between two measures because of a third variable that is not directly measured. So, just because we find a correlation, does not mean we can conclude anything about a causal connection between two measurements.
For example, in one of Dr. MO's courses, she found a positive correlation between the number of pens in students' bags and their final grade percentage. Does having more pens actually cause students to learn more and earn more points? Probably not. It's mroe likely that students are maybe over-achievers or want to be totally prepared have more pens in their bags, and also study in ways that result in learning.
Correlation and Random Chance: Sometimes there's a correlation that's really a Type I Error
Another very important aspect of correlations is the fact that they can be produced by random chance. This means that you can find a statistically significant correlation between two measures, even when they have absolutely nothing to do with one another. You might have hoped to find zero correlation when two measures are totally unrelated to each other. Although this certainly happens, unrelated measures can accidentally produce spurious correlations, just by chance alone.
Let's get back to the final grades and pens-in-the-bag example. Once Dr. MO found that correlation, she's tried to replicate it with other classes for several years, and has never been able to. It appears that we had one wonky sample that produced a signficant correlation, but that there is actually no real correlation between pens and grades in the population of students.
Watching Random Correlations
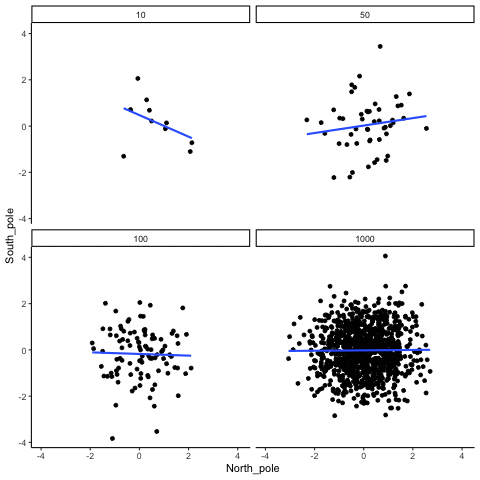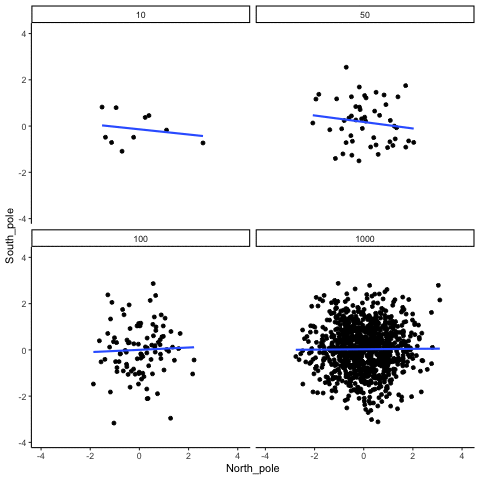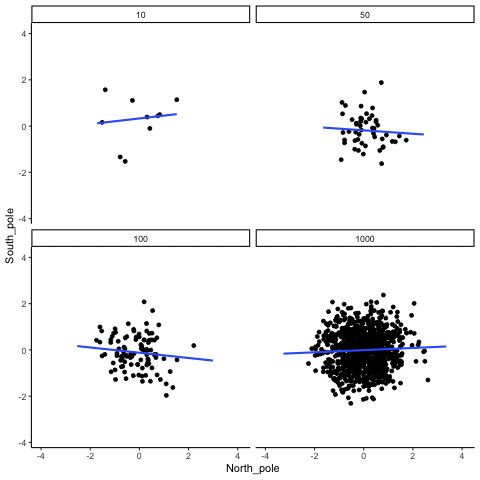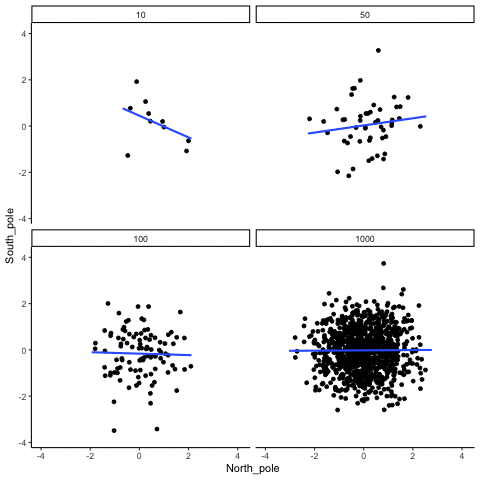
In Figure \(\PageIndex{2}\), Dr. Crump wrote code to randomly sample numbers for two variables, plot them, and show the correlation using a line. There are four panels, each showing the number of observations in the samples (N), from 10, 50, 100, to 1,000 in each sample.
Remember, because these are randomly sampled numbers, there should be no relationship between the two variables. But, as we have been discussing, because of chance, we can sometimes observe a correlation due to chance alone, a Type I Error. The important thing to watch is how the line behaves across the four panels when you see these online. This line shows the best-fit line for all of the data. The closer that the dots are to the line, the stronger the correlation. As you can see, the line twirls around in all directions when the sample size is 10. It is also moves around quite a bit when the sample size is 50 or 100. It still moves a bit when the sample size is 1,000, but much less. In all cases we expect that the line should be parallel with the horizon (x-axis), but every time there's a new sample, sometimes the line shows us pseudo patterns. The best fit line is not very stable for small sample-sizes, but becomes more reliably flat as sample-size increases.

Which line should you trust? Well, hopefully you can see that the line for 1000 samples is the most stable. It tends to be parallel to the horizon every time, and it does not depend so much on the particular sample. The line with 10 observations per sample goes all over the place. The take home here, is that if someone told you that they found a correlation, you should want to know how many observations they hand in their sample. If they only had 10 observations, how could you trust the claim that there was a correlation? You can’t!!! Not now that you know samples that are that small can do all sorts of things by chance alone. If instead, you found out the sample was very large, then you might trust that finding a little bit more. For example, in the above movie you can see that when there are 1000 samples, we never see a strong or weak correlation; the line is always flat. This is because chance almost never produces strong correlations when the sample size is very large.
In the above example, we sampled numbers random numbers from a uniform distribution. Many examples of real-world data will come from a normal or approximately normal distribution. We can repeat the above, but sample random numbers from the same normal distribution. There will still be zero actual correlation between the X and Y variables, because everything is sampled randomly. But, we still see the same behavior as above. The computed correlation for small sample-sizes fluctuate wildly, and large sample sizes do not.
OK, so what do things look like when there actually is a correlation between variables?
Watching Real Correlations
Sometimes there really are correlations between two variables that are not caused by chance. Figure \(\PageIndex{4}\) has four more animated scatter plots. Each shows the correlation between two variables. Again, we change the sample-size in steps of 10, 50 100, and 1,000. The data have been programmed to contain a real positive correlation (as the scores on the x-axis variable increase, scores on the y-axis variable should also increase). Positive correlations have a trend that goes up and to the right. So, we should expect that the line will be going up from the bottom left to the top right. However, there is still variability in the data. So this time, sampling error due to chance will fuzz the correlation. We know it is there, but sometimes chance will cause the correlation to be eliminated.
Notice that in the top left panel (sample-size 10), the line is twirling around much more than the other panels. Every new set of samples produces different correlations. Sometimes, the line even goes flat or downward. However, as we increase sample-size, we can see that the line doesn’t change very much, it is always going up showing a positive correlation.

The main takeaway here is that even when there is a positive correlation between two things, you might not be able to see it if your sample size is small. For example, you might get unlucky with the one sample that you measured, like the sample that Dr. MO found with her pen data. Your sample could show a negative correlation, even when the actual correlation is positive! Unfortunately, in the real world we usually only have the sample that we collected, so we always have to wonder if we got lucky or unlucky.


