2.3: Graphical Displays

Last updated
Save as PDF

Page ID: 44193

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$\newcommand{\avec}{\mathbf a}$ $\newcommand{\bvec}{\mathbf b}$ $\newcommand{\cvec}{\mathbf c}$ $\newcommand{\dvec}{\mathbf d}$ $\newcommand{\dtil}{\widetilde{\mathbf d}}$ $\newcommand{\evec}{\mathbf e}$ $\newcommand{\fvec}{\mathbf f}$ $\newcommand{\nvec}{\mathbf n}$ $\newcommand{\pvec}{\mathbf p}$ $\newcommand{\qvec}{\mathbf q}$ $\newcommand{\svec}{\mathbf s}$ $\newcommand{\tvec}{\mathbf t}$ $\newcommand{\uvec}{\mathbf u}$ $\newcommand{\vvec}{\mathbf v}$ $\newcommand{\wvec}{\mathbf w}$ $\newcommand{\xvec}{\mathbf x}$ $\newcommand{\yvec}{\mathbf y}$ $\newcommand{\zvec}{\mathbf z}$ $\newcommand{\rvec}{\mathbf r}$ $\newcommand{\mvec}{\mathbf m}$ $\newcommand{\zerovec}{\mathbf 0}$ $\newcommand{\onevec}{\mathbf 1}$ $\newcommand{\real}{\mathbb R}$ $\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$ $\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$ $\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$ $\newcommand{\laspan}[1]{\text{Span}\{#1\}}$ $\newcommand{\bcal}{\cal B}$ $\newcommand{\ccal}{\cal C}$ $\newcommand{\scal}{\cal S}$ $\newcommand{\wcal}{\cal W}$ $\newcommand{\ecal}{\cal E}$ $\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$ $\newcommand{\gray}[1]{\color{gray}{#1}}$ $\newcommand{\lgray}[1]{\color{lightgray}{#1}}$ $\newcommand{\rank}{\operatorname{rank}}$ $\newcommand{\row}{\text{Row}}$ $\newcommand{\col}{\text{Col}}$ $\renewcommand{\row}{\text{Row}}$ $\newcommand{\nul}{\text{Nul}}$ $\newcommand{\var}{\text{Var}}$ $\newcommand{\corr}{\text{corr}}$ $\newcommand{\len}[1]{\left|#1\right|}$ $\newcommand{\bbar}{\overline{\bvec}}$ $\newcommand{\bhat}{\widehat{\bvec}}$ $\newcommand{\bperp}{\bvec^\perp}$ $\newcommand{\xhat}{\widehat{\xvec}}$ $\newcommand{\vhat}{\widehat{\vvec}}$ $\newcommand{\uhat}{\widehat{\uvec}}$ $\newcommand{\what}{\widehat{\wvec}}$ $\newcommand{\Sighat}{\widehat{\Sigma}}$ $\newcommand{\lt}{<}$ $\newcommand{\gt}{>}$ $\newcommand{\amp}{&}$ $\definecolor{fillinmathshade}{gray}{0.9}$

Statistical graphs are useful in getting the audience’s attention in a publication or presentation. Data presented graphically is easier to summarize at a glance compared to frequency distributions or numerical summaries. Graphs are useful to reinforce a critical point, summarize a data set, or discover patterns or trends over a period of time. Florence Nightingale (1820-1910) was one of the first people to use graphical representations to present data. Nightingale was a nurse in the Crimean War and used a type of graph that she called polar area diagram, or coxcombs to display mortality figures for contagious diseases such as cholera and typhus.

Nightingale

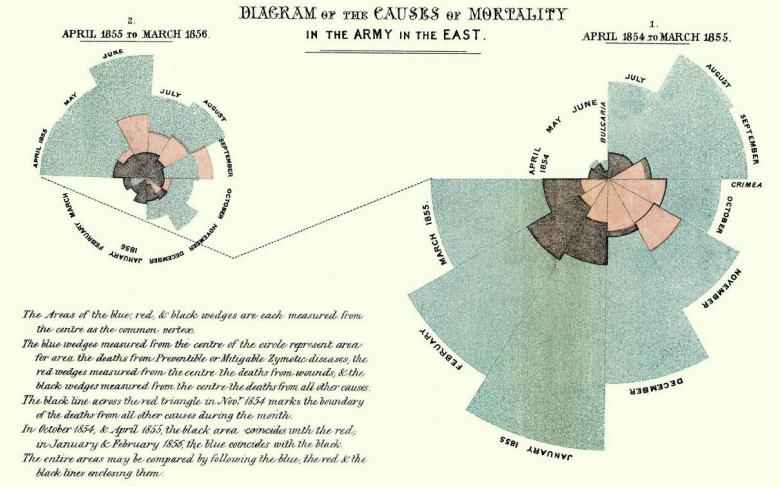
Nightingale-mortality.jpg. (2021, May 18). Wikimedia Commons, the free media repository. Retrieved July 2021 from https://commons.wikimedia.org/w/index.php?title=File:Nightingale-mortality.jpg&oldid=561529217.

It is hard to provide a complete overview of the most recent developments in data visualization with the onset of technology. The development of a variety of highly interactive software has accelerated the pace and variety of graphical displays across a wide range of disciplines.

2.3.1 Stem-and-Leaf Plot

Stem-and-leaf plots (or stemplots) are a useful way of getting a quick picture of the shape of a distribution by hand. Turn the graph sideways and you can see the shape of your data. You can now easily identify outliers. Each observation is divided into two pieces; the stem and the leaf. If the number is just two digits then the stem would be the tens digit and the leaf would be the ones digit. When a number is more than two digits then the cut point should split the data into enough classes that is useful to see the shape of the data.

To create a stem-and-leaf plot:

Separate each observation into a stem and a leaf.
Write the stems in a vertical column in ascending order (from smallest to largest). Fill in missing numbers even if there are gaps in the data. Draw a vertical line to the right of this column.
Write each leaf in the row to the right of its stem, in increasing order.

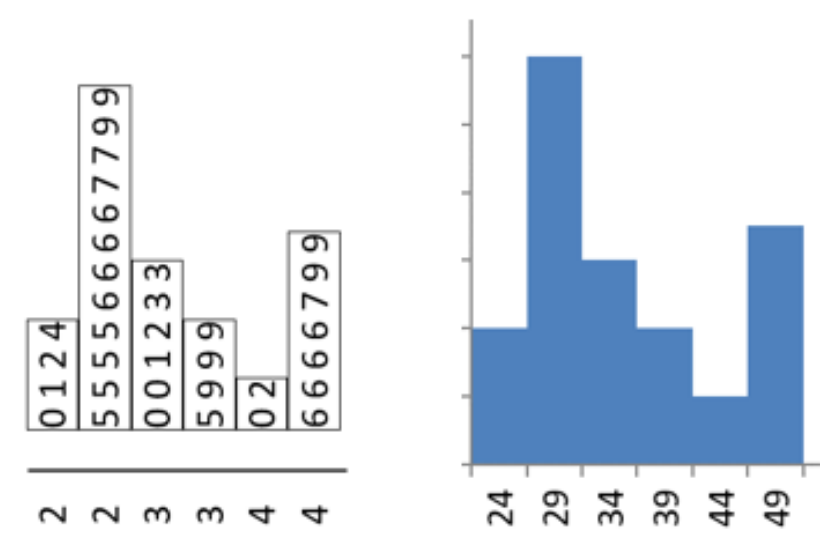
Create a stem-and-leaf plot for the sample of 35 ages.

46 47 49 25 46 22 42 24 46 40 39 27 25 30 33 27 46 21 29 20 26 25 25 26 35 49 33 26 32 31 39 30 39 29 26

Solution

Divide each number so that the tens digit is the stem and the ones digit is the leaf. The smallest observation is 20. The stem = 2 and the leaf = 0. The next value is 21 and the stem = 2 and the leaf = 1, up to the last value of 49 which would have a stem = 4 and a leaf = 9. If we use the tens categories we have the stems 2, 3 and 4. Line up the stems without skipping a number even if there are no values in that stem. In other words, the stems should have equal spacing (for example, count by ones, tens, hundreds, thousands, etc.). Then place a vertical line to the right of the stems. In each row put the leaves with a space between each leaf. Sort each row from smallest to largest. In Figure 2- 6 the 2 | 0 = 20.

\begin{array}{l|llllllllllllllll}
2 & 0 & 1 & 2 & 4 & 5 & 5 & 5 & 5 & 6 & 6 & 6 & 6 & 7 & 7 & 9 & 9 \\
3 & 0 & 0 & 1 & 2 & 3 & 3 & 5 & 9 & 9 & 9 \\
4 & 0 & 2 & 6 & 6 & 6 & 6 & 7 & 9 & 9
\end{array}

Figure 2-6

It is hard to see the shape with so few classes and so many leaves in each class.

We can break each stem in half, putting leaves 0-4 in the first row and 5-9 in the second row, as in Figure 2-7.

\begin{array}{l|llllllllllll}
2 & 0 & 1 & 2 & 4 \\
2 & 5 & 5 & 5 & 5 & 6 & 6 & 6 & 6 & 7 & 7 & 9 & 9 \\
3 & 0 & 0 & 1 & 2 & 3 & 3 \\
3 & 5 & 9 & 9 & 9 \\
4 & 0 & 2 \\
4 & 6 & 6 & 6 & 6 & 7 & 9 & 9
\end{array}

Figure 2-7

Now, add labels and make sure the leaves are in ascending order. Be careful to line the leaves up in columns. You need to be able to compare the lengths of the rows when you interpret the graph.

Imagine lines around the leaves and turn the graph 90 degrees to the left. You can now see in Figure 2-8 the shape of the distribution. Note that Excel uses the upper class limit for the axis label.

Figure 2-8

If a leaf takes on more than the ones category then supply a footnote at the bottom of the plot with the units.

A small sample of house prices in thousands of dollars was collected: 375, 189, 432, 225, 305, 275. Make a stem-and-leaf plot.

Solution

If we were to split the stem and leaf between the ones and tens place, then we would need stems going from 18 up to 43. Twenty-six stems for only six data points is too many. The next break then for a stem would be between the tens and hundreds. This would give stems from 1 to 4. Then each leaf will be the ones and tens. For example, then number 375 would have a stem = 3 and a leaf = 75.

\begin{array}{l|ll}
1 & 89 \\
2 & 25 & 75 \\
3 & 05 & 75 \\
4 & 32
\end{array}

Leaf = $1000

A small sample of coffee prices: 3.75, 1.89, 4.32, 2.25, 3.05, 2.75 was collected. Make a stem-and-leaf plot.

Solution

\begin{array}{l|ll}
1 & 89 \\
2 & 25 & 75 \\
3 & 05 & 75 \\
4 & 32
\end{array}

Leaf = $0.01

Note that the last two stem-and-leaf plots look identical except for the footnote. It is important to include units to tell people what the stems and leaves mean by inserting a legend.

Back-to-back stem-and-leaf plots let us compare two data sets on the same number line. The two samples share the same set of stems. The sample on the right is written backward from largest leaf to smallest leaf, and the sample on the left has leaves from smallest to largest.

Use the following back-to-back stem-and-leaf plot to compare pulse rates before and after exercise.

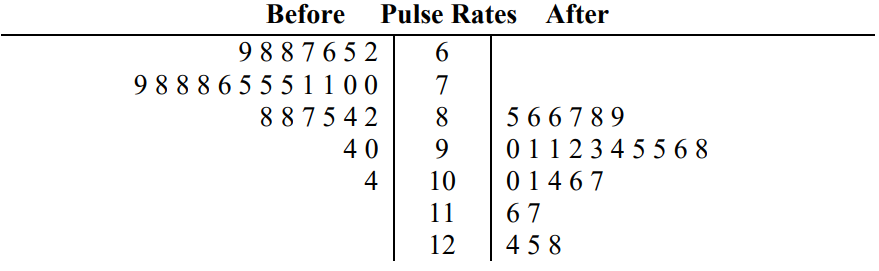
Solution

The group on the left has leaves going in descending order and represent the pulse rates before exercise. The stems are in the middle column. The group on the right has leaves going in ascending order and represent the pulse rates after exercise. The first row has pulse rates of 62, 65, 66, 67, 68, 68 and 69. The last row of pulse rates are 124, 125, and 128.

2.3.2 Histogram

A histogram is a graph for quantitative data (we call these bar graphs for qualitative data). The data is divided into a number of classes. The class limits become the horizontal axis demarcated with a number line and the vertical axis is either the frequency or the relative frequency of each class. Figure 2-9 is an example of a histogram.

The histogram for quantitative data looks similar to a bar graph, except there are some major differences.

First, in a bar graph the categories can be put in any order on the horizontal axis. There is no set order for these nominal data. You cannot say how the data is distributed based on the shape, since the shape can change just by putting the categories in different orders. With quantitative data, the data are in a specific order, since you are dealing with numbers. With quantitative data, you can talk about a distribution shape.

This leads to the second difference from bar graphs. In a bar graph, the categories that you made in the frequency table were the words used for the category name. In quantitative data, the categories are numerical categories, and the numbers are determined by how many classes you choose. If two people have the same number of categories, then they will have the same frequency distribution. Whereas in qualitative data, there can be many different categories depending on the point of view of the author.

The third difference is that the bars touch with quantitative data, and there will be no gaps in the graph. The reason that bar graphs have gaps is to show that the categories do not continue on, as they do in quantitative data. Since the graph for quantitative data is different from qualitative data, it is given a different name of histogram.

Some key features of a histogram:

Equal spacing on each axis
Bars are the same width
Label each axis and title the graph
Show the scale on the frequency axis
Label the categories on the category axis
The bars should touch at the class boundaries

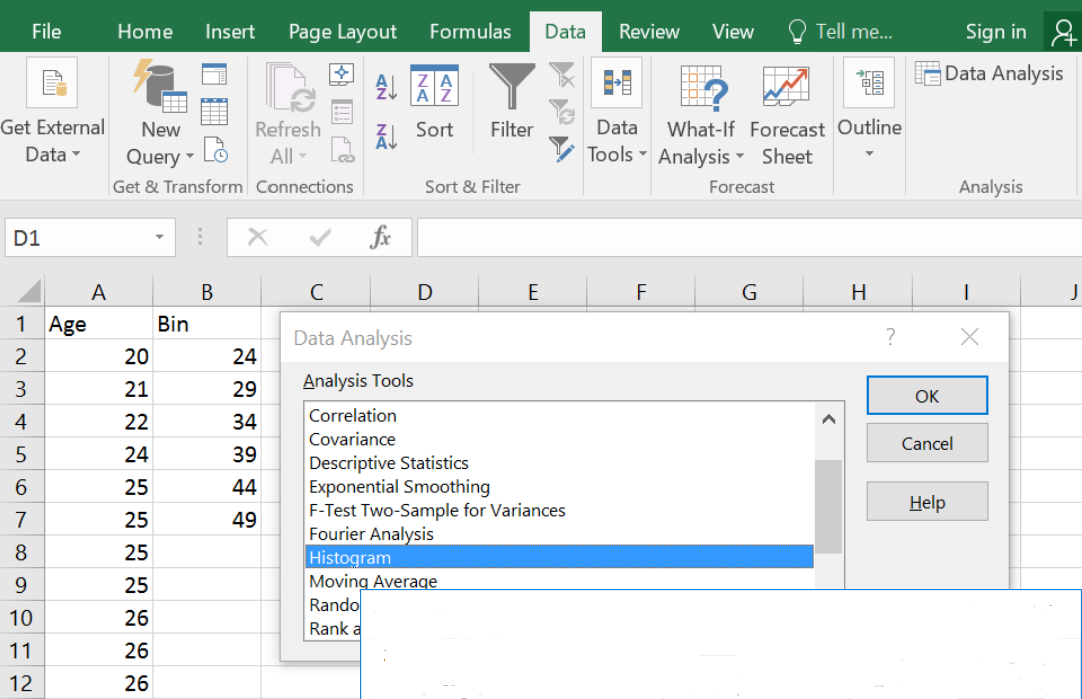
To create a histogram, you must first create a frequency distribution. Software and calculators can create histograms easily when a large amount of sample data is being analyzed.

Excel

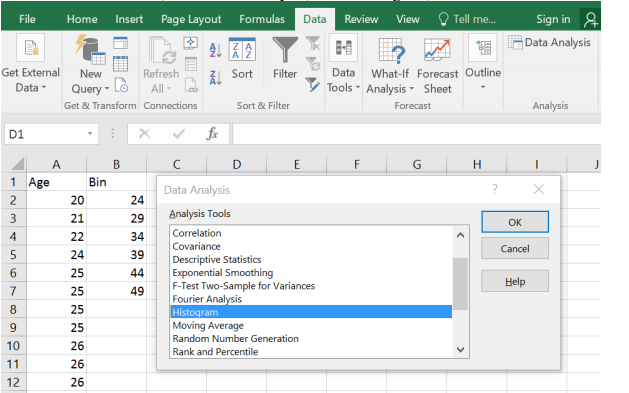
To create a histogram in Excel you will need to first install the Data Analysis tool.

If your Data Analysis is not showing in the Data tab, follow the directions for installing the free add-in here: https://support.office.com/en-us/article/Load-the-Analysis-ToolPak-in-Excel-6a63e598-cd6d-42e3-9317- 6b40ba1a66b4.

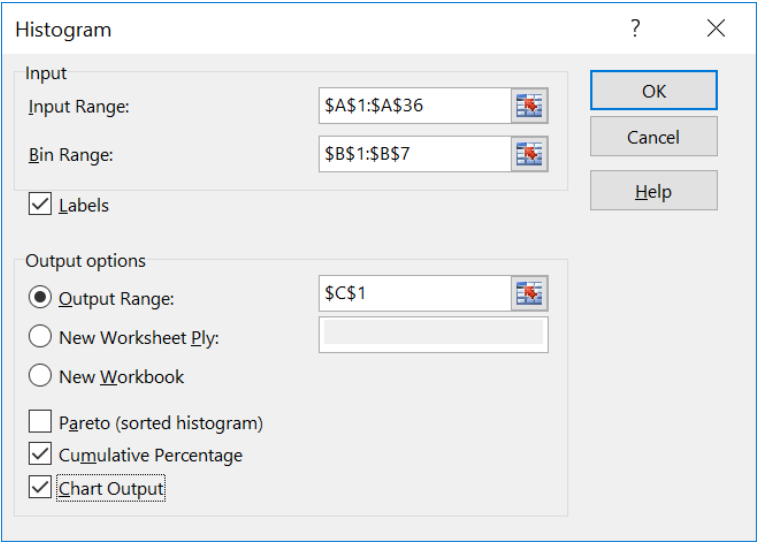
Type in the data into one blank column in any order. If you want to have class widths other than Excel’s default setting, type in a new column the endpoints of each class found in your frequency distribution, these are called the bins in Excel.

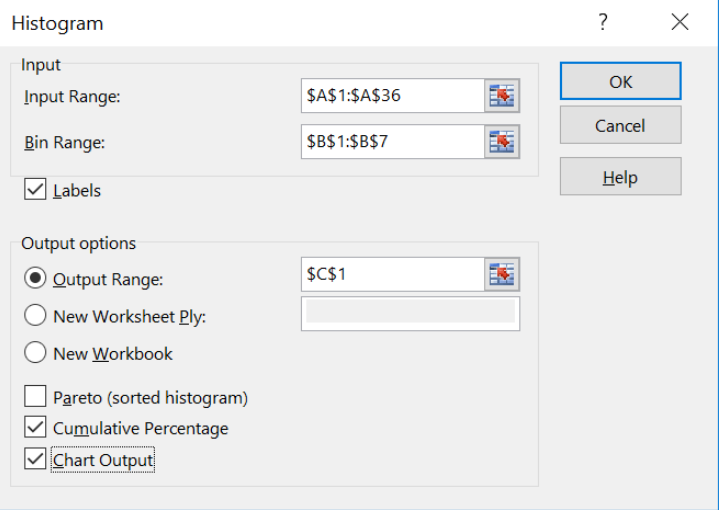
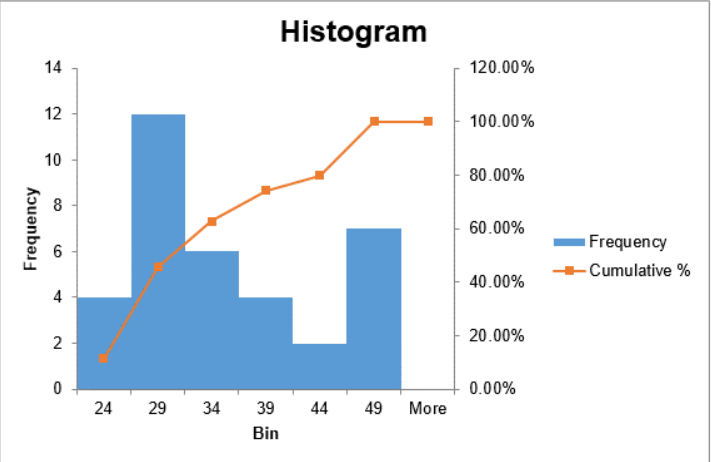
Using the sample of 35 ages, make a histogram using Excel.

46 47 49 25 46 22 42 24 46 40 39 27 25 30 33 27 46 21 29 20 26 25 25 26 35 49 33 26 32 31 39 30 39 29 26

Solution

Type the data in any order into column A and the bins in order in column B as shown below. Then select the Data tab, select Data Analysis, select Histogram, then select OK.

In the dialogue box, click into the Input Range box, then use your mouse and highlight the ages including the label.

Then click into the Bin Range box and use your mouse to highlight the bins including the label.

Select the box for Labels only if you included the labels in your ranges. You can have your output default to a new worksheet, or select the circle to the left of Output Range, click into the box to the right of Output Range and then select one blank cell on your spreadsheet where you want the top left-hand corner of your table and graph to start. Then check the boxes next to Cumulative Percentage and Chart Output. Then select OK, and see below.

A histogram needs to have bars that touch, which is not the default in Excel. To get the bars to touch, right-click on one of the blue bars and select Format Data Series and slide the Gap Width to 0%.

Excel produces both a frequency table and a histogram. The table has the frequencies and the cumulative relative frequencies.

Bin	Frequency	Cumulative %
24	4	11.43%
29	12	45.71%
34	6	62.86%
39	4	74.29%
44	2	80.00%
49	7	100.00%
More	0	100.00%

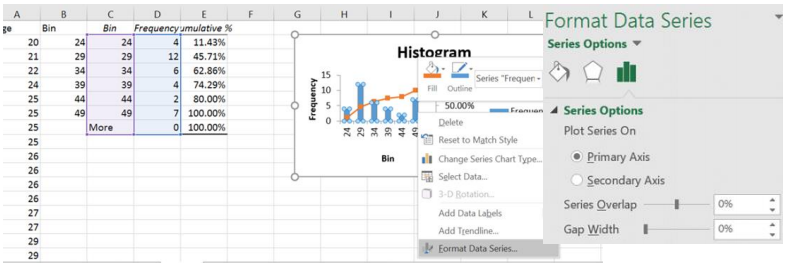
The histogram has bars for the height of each frequency and then makes a line graph of the cumulative relative frequencies over the bars. This red line is a line graph of the cumulative relative frequencies, also called an ogive and is discussed in a later section.

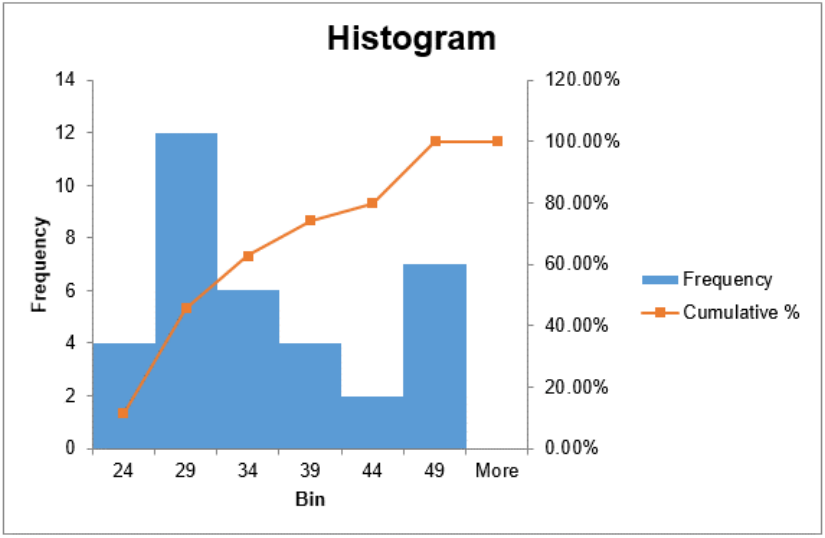
It is important to note that the number of classes that are used and the value of the first class boundary will change the shape of the histogram.

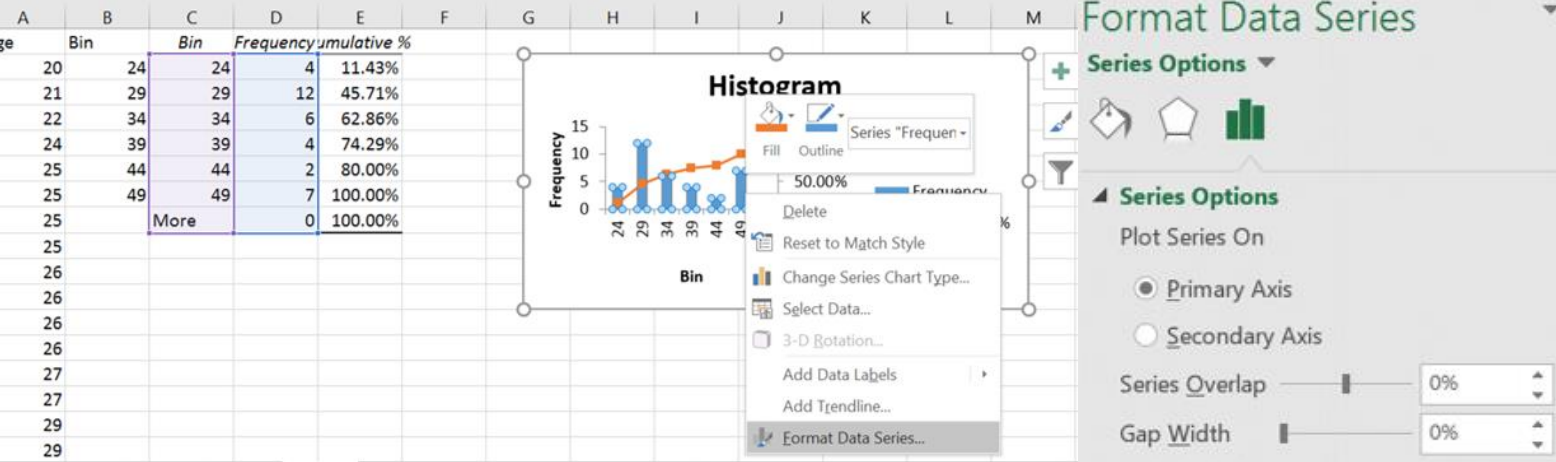
A relative frequency histogram is when the relative frequencies are used for the vertical axis instead of the frequencies and the y-axis will represent a percent instead of the number of people.

In Excel, after you create your histogram, you can manually change the frequency column to the relative frequency values by dividing each number by the sample size. Here is a screen shot just as the last number was changed, note as soon as you hit enter the bars will shrink and adjust.

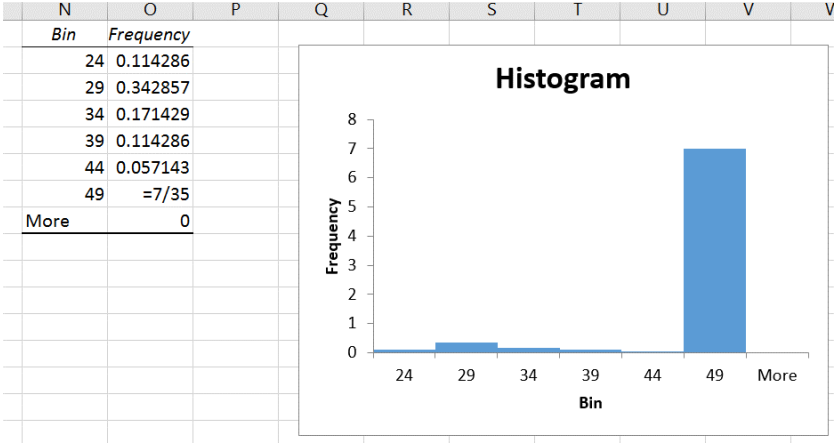
After the last value =7/35 was entered and the label changed to Relative Frequency you get the following graph.

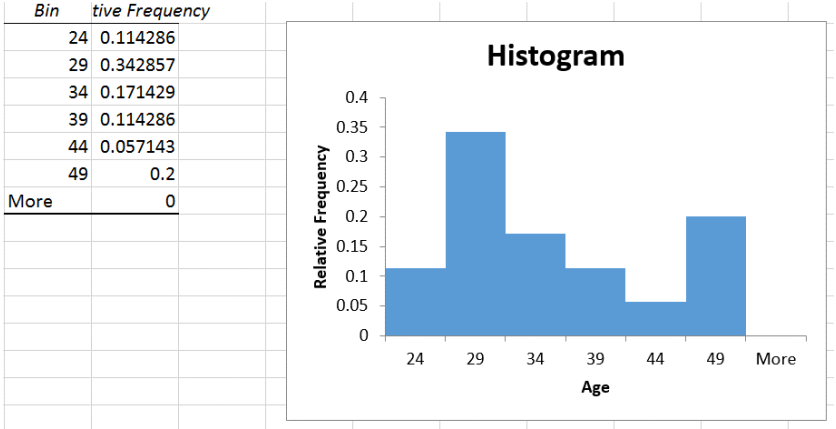
The shape of the histogram will be the same for the relative frequency distribution and the frequency distribution; the height, though, is the proportion instead of frequency.

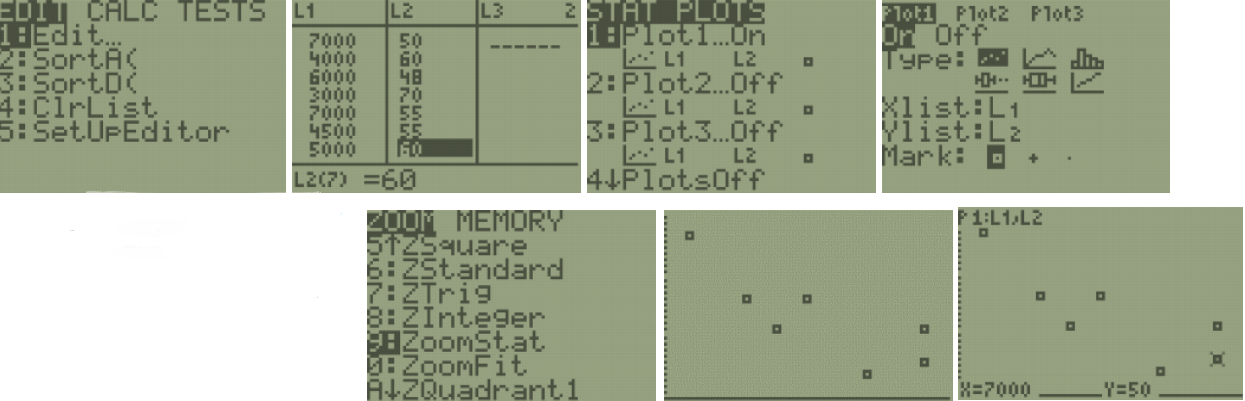
TI-84: To make a histogram, enter the data by pressing [STAT]. The first option is already highlighted (1:Edit) so you can either press [ENTER] or [1]. Make sure the cursor is in the list, not on the list name and type the desired values pressing [ENTER] after each one.

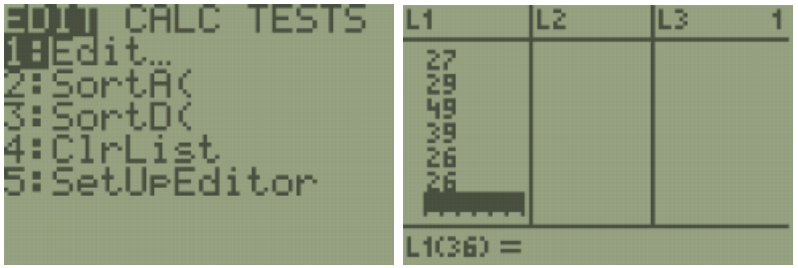
Press [2nd] [QUIT] to return to the home screen. To clear a previously stored list of data values, arrow up to the list name you want to clear, press [CLEAR], and then press enter. An alternative way is press [STAT], press 4 for 4:ClrList, press [2nd], then press the number key corresponding to the data list you wish to clear, for example, [2^nd] [1] will clear L₁, then press [ENTER]. After you enter the data, press [2^nd] [STAT PLOT]. Select the first plot by hitting [Enter] or the number [1:Plot 1]. Turn the plot [On] by moving the cursor to On and selecting Enter. Select the Histogram option using the right arrow keys. Select [Zoom], then [ZoomStat].

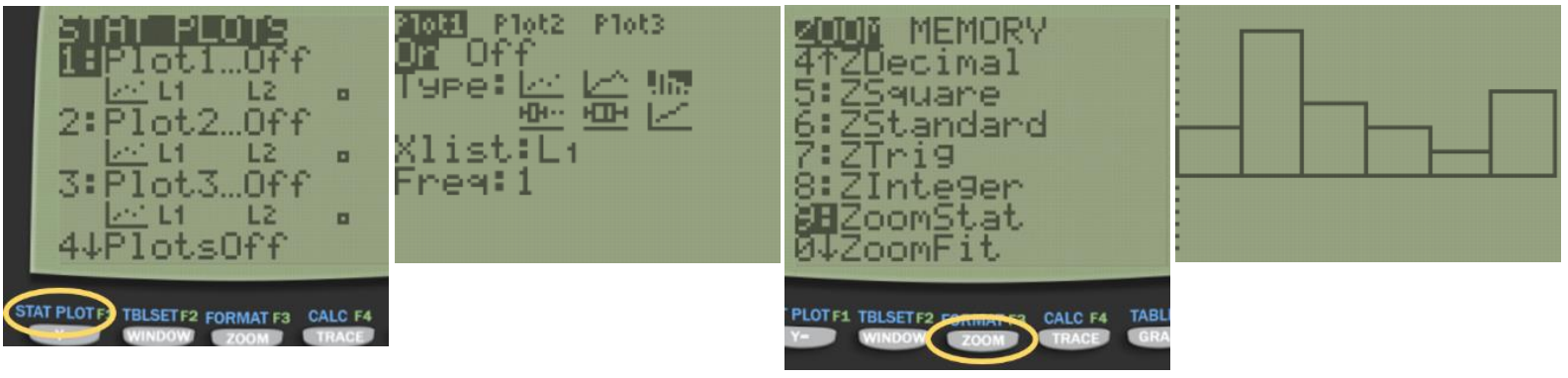
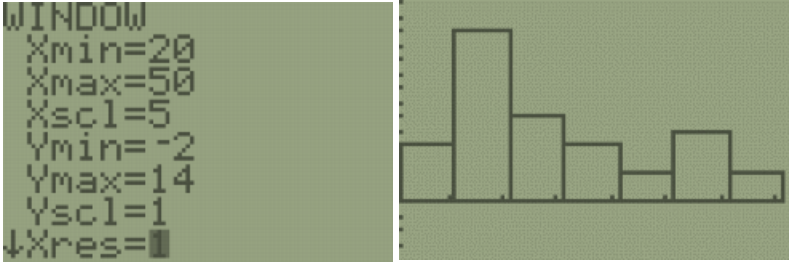
You can see and change the class width by selecting [Window], then change the minimum x value Xmin=20, the maximum x value Xmax=50, the x-scale to Xscl=5 and the minimum y value Ymin=-6.5 and the maximum y value to Ymax=14. Select the [GRAPH] button. We get a similar looking Histogram compared to the stem-and-leaf plot and Excel histogram. Select the [TRACE] button to see the height of each bar and the classes.

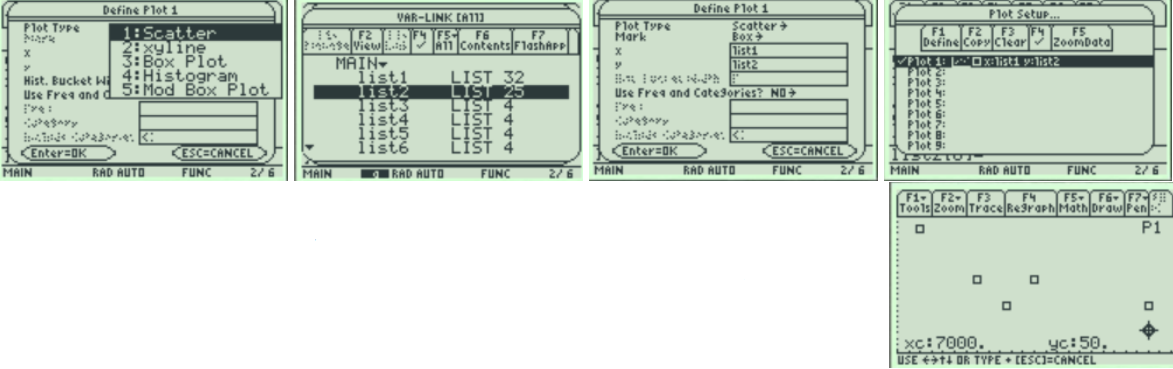
TI-89: First, enter the data into the Stat/List editor under list 1. Press [APP] then scroll down to Stat/List Editor, on the older style TI-89 calculators, go into the Flash/App menu, and then scroll down the list. Make sure the cursor is in the list, not on the list name, and type the desired values pressing [ENTER] after each one. To clear a previously stored list of data values, arrow up to the list name you want to clear, press [CLEAR], and then press enter. After you enter the data, select Press [F2] Plots, scroll down to [1: Plot Setup] and press [Enter].

Select [F1] Define. Use your arrow keys to select Histogram for Type, and then scroll down to the x-variable box. Press [2^nd] [Var-Link] this key is above the [+] sign. Then arrow down until you find your List1 name under the Main file folder. Then press [Enter] and this will bring the name List1 back to the menu. You will now see that Plot1 has a small picture of a histogram. To view the histogram, select [F5] [Zoom Data].

The histogram looks a little different from Excel; you can change the settings for the bucket to match your table. Press [♦] [F2:Window]. Change the minimum x value xmin=20, the maximum x value xmax=50, the x-scale to xscl=5 and the minimum y value ymin=-6.5 and the maximum y value to ymax=14. Then press the [♦] [F3:GRAPH] button. Select [F3:Trace] to see the frequency for each bar. Then use your left and right arrow keys to move to the other bars.

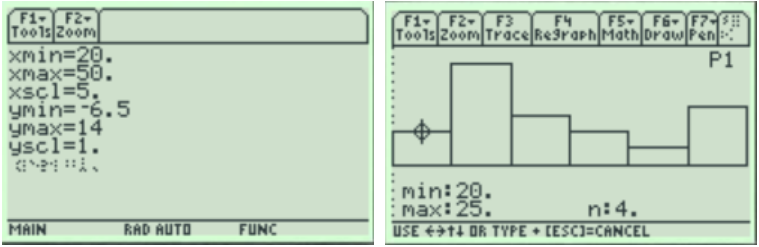
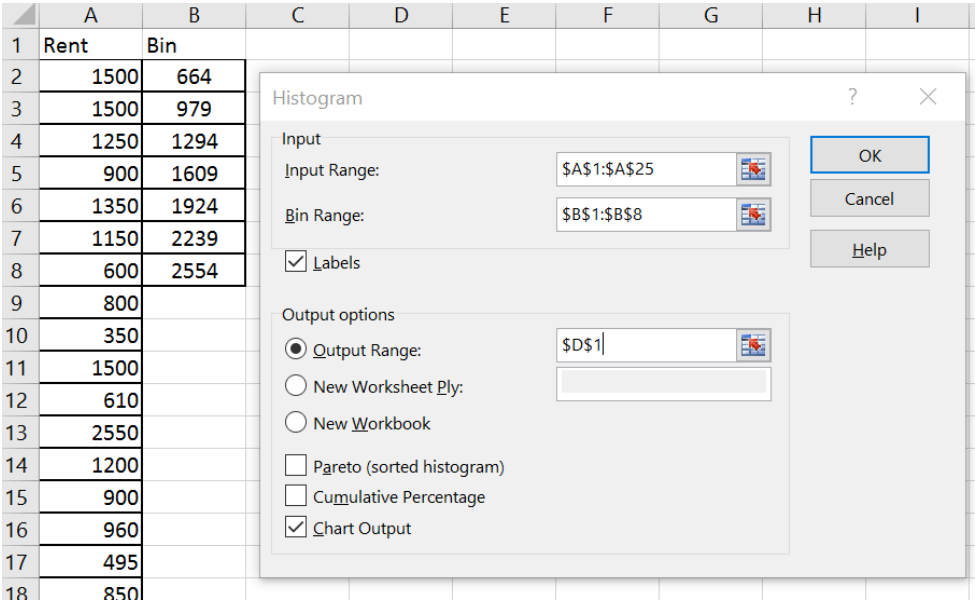
Make a histogram for the following random sample of student rent prices using Excel.

1500 1350 350 1200 850 900 1500 1150 1500 900 1400 1100 1250 600 610 960 890 1325 900 800 2550 495 1200 690

Solution

Start by making a relative frequency distribution table with 7 classes.

Find the range: largest value – smallest value = 2550 – 350 = 2200, range = $2,200.
Find the class width: width = $\frac{\text { range }}{\text { 7 }}$ = $\frac{\text { 2000 }}{\text { 7 }}$ ≈ 314.286. Round up to 315. Always round up to the next integer even if the width is already an integer.
Find the class limits: Start at the smallest observation. This is the lower class limit for the first class. Add the class width to get the lower limit of the next class. Keep adding the class width to get all the lower limits, 350 + 315 = 665, 665 + 315 = 980, 980 + 315 = 1295, etc. The upper limit is one unit less than the next lower limit: so, for the first class the upper class limit would be 665 – 1 = 664. When you have all 7 classes, make sure the last number, in this case the 2550, is at least as large as the largest value in the data. If not, you made a mistake somewhere.

Using Excel: Type the raw data in Excel in column A, the right-hand class endpoints for the bins in column B. Select Data, Data Analysis, Histogram.

Select the Input Range, Bin Range, Labels (if you selected them), output option, Chart Output, then OK.

See finished histogram below in Figure 2-13.

Figure 2-10

By hand: Tally and find the frequency of the data.

Frequency Distribution for Monthly Rent

Class Limits	Tally	Frequency	Relative Frequency
350-664	4	4	0.1667
665-979	8	8	0.333
980-1294	5	5	0.2083
1295-1609	6	6	0.25
1610-1924	0	0	0
1925-2239	0	0	0
2240-2554	1	1	0.0417
Total	0	24	1

Figure 2-11

Make sure the total of the frequencies is the same as the number of data points and the total of the relative frequency is one. Since we want the bars on the histogram to touch, the number line needs to use the class boundaries that are half way between the endpoints of the class limits. Start by finding the distance between the class endpoints and divide by two: (665-664)/2 = 0.5. Then subtract 0.5 from the left-hand side of each class limit and this will give you the points to use on the x-axis: 349.5, 664.5, 979.5, 1294.5, 1609.5, 1924.5, 2239.5, and 2554.5. Then draw your graph as in Figure 2-12. You can use frequencies or relative frequencies for the y-axis.

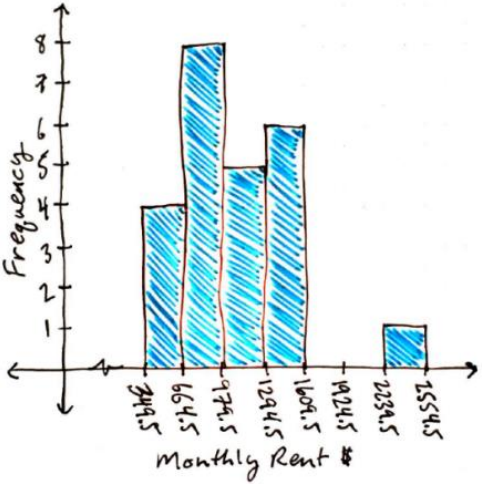
Figure 2-12

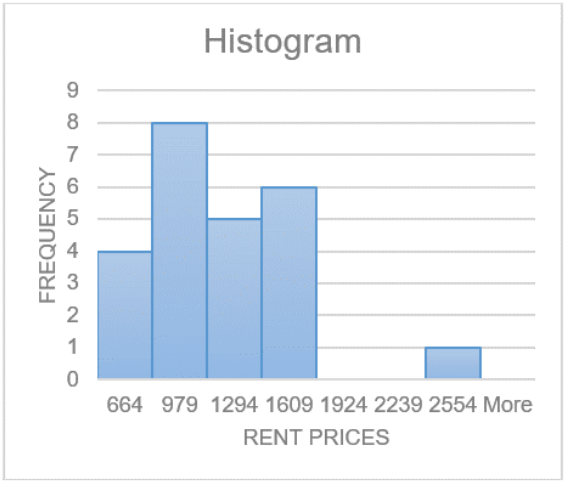
Figure 2-13

Reviewing the graph in Figure 2-13, you can see that most of the students pay around $750 per month for rent, with about $1,500 being the other common value. Most students pay between $600 and $1,600 per month for rent. Of course, these values are just estimates pulled from the graph.

There is a large gap between the $1,500 class and the highest data value. This seems to say that one student is paying a great deal more than everyone else is. This value may be an outlier.

An outlier is a data value that is far from the rest of the values. It may be an unusual value or a mistake. It is a data value that should be investigated. In this case, the student lives in a very expensive part of town, thus the value is not a mistake, and is just very unusual. There are other aspects that can be discussed, but first some other concepts need to be introduced.

2.3.3 Ogive

The line graph for the cumulative or cumulative relative frequency is called an ogive (oh-jyve). To create an ogive, first create a scale on both the horizontal and vertical axes that will fit the data. Then plot the points of the upper class boundary versus the cumulative (or cumulative relative) frequency. Make sure you include the point with the lowest class and the zero cumulative frequency. Then just connect the dots.

The steeper the line the more accumulation occurs across the corresponding class. If the line is flat then the frequency for that class is zero. The ogive graph will always be going uphill from left to right and should never dip below the previous point. Figure 2-14 is an example of an ogive.

Ogive comes from the uphill shape used in architecture. Here is an example of an ogive in the East Hall staircase at PSU.

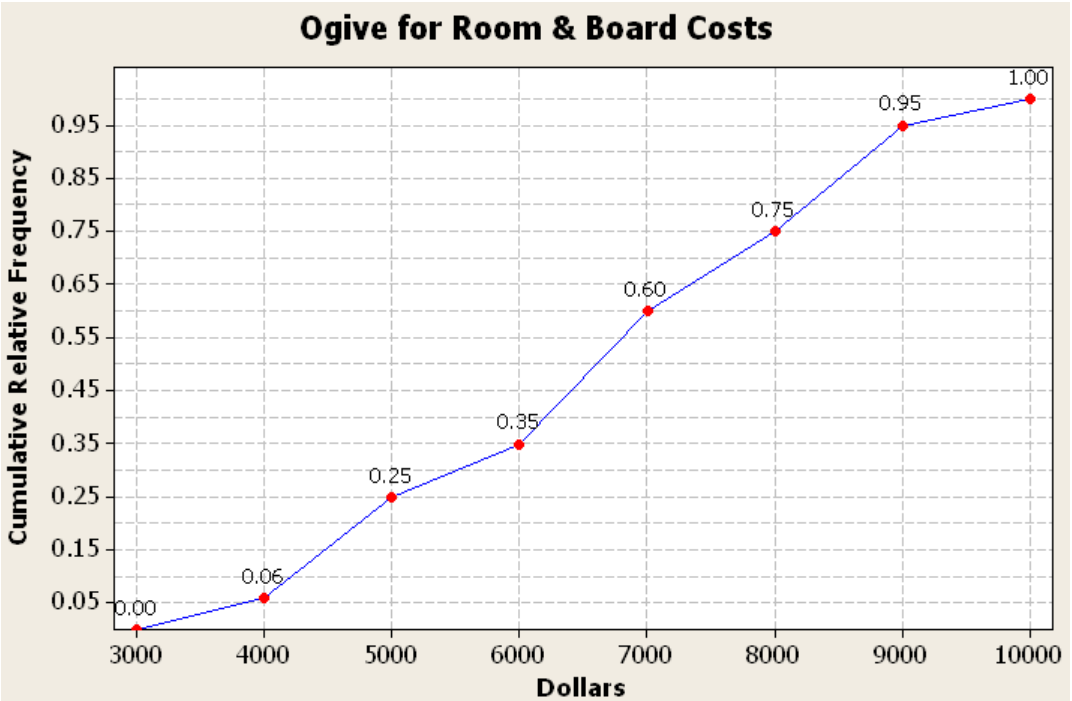
Figure 2-14

Make an ogive for the following random sample of rent prices students pay with the corresponding cumulative frequency distribution table.

1500 1350 350 1200 850 900 1250 600 610 960 890 1325 1500 1150 1500 900 1400 1100 900 800 2550 495 1200 690

Class Limits	Frequency	Cumulative Frequency
350 - 664	4	4
665 - 979	8	12
980 - 1294	5	17
1295 - 1609	6	23
1610 - 1924	0	23
1925 - 2239	0	23
2240 - 2554	1	24

Solution

Find the class boundaries, 349.5, 664.5 … use these for the tick mark labels on the horizontal x-axis, the same as what was used for the histogram. The y-axis uses the cumulative frequencies. The largest cumulative frequency is 24. Every third number is marked on the y-axis units. See Figure 2-15 and Figure 2-16.

By hand:

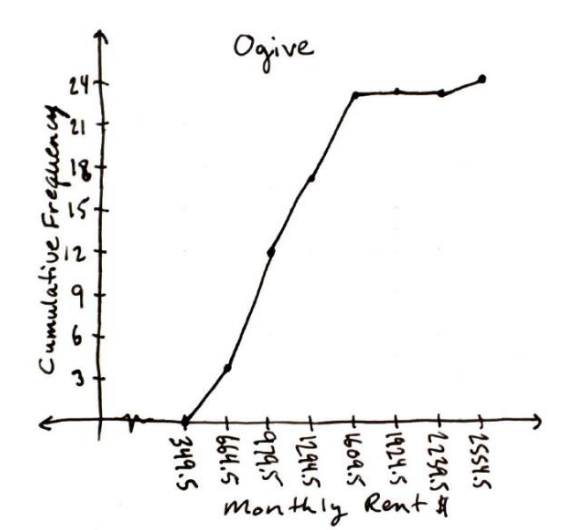
Figure 2-15

Using software:

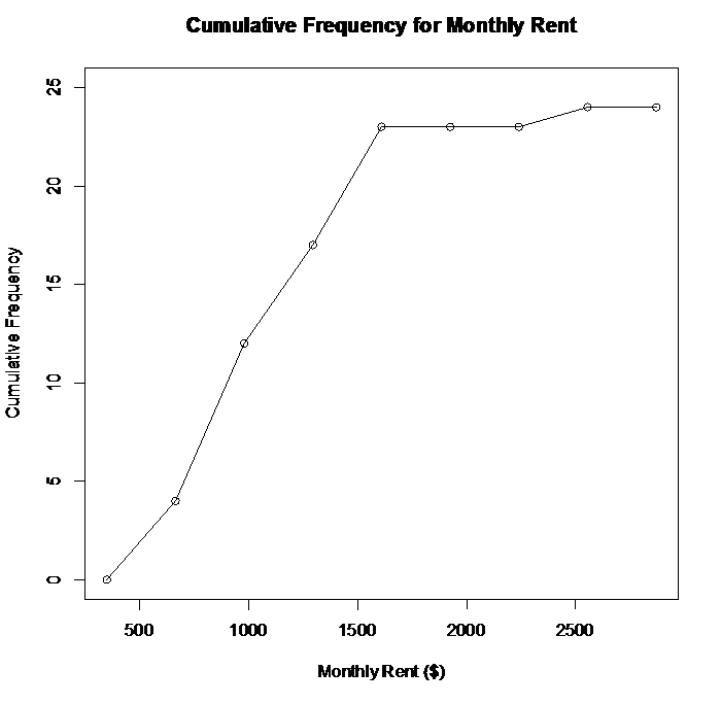
Figure 2-16

The usefulness of an ogive is to allow the reader to find out how many students pay less than a certain value, and what amount of monthly rent a certain number of students pay.

For instance, if you want to know how many students pay less than $1,500 a month in rent, then you can go up from the $1,500 until you hit the line and then you go left to the cumulative frequency axis to see what cumulative frequency corresponds to $1,500. It appears that around 21 students pay less than $1,500. See Figure 2-17.

If you want to know the cost of rent that 15 students pay less than, then you start at 15 on the vertical axis and then go right to the line and down to the horizontal axis to the monthly rent of about $1,200. You can see that about 15 students pay less than about $1,200 a month. See Figure 2-18.

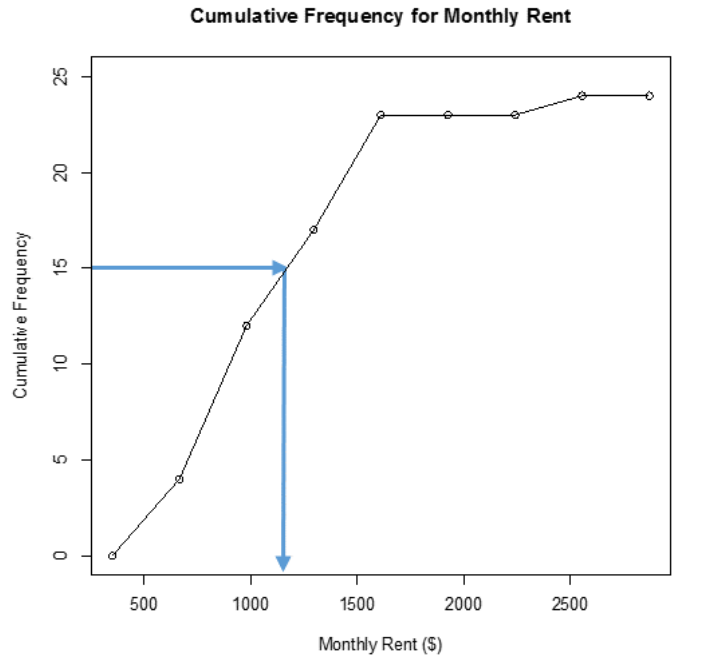
Figure 2-17

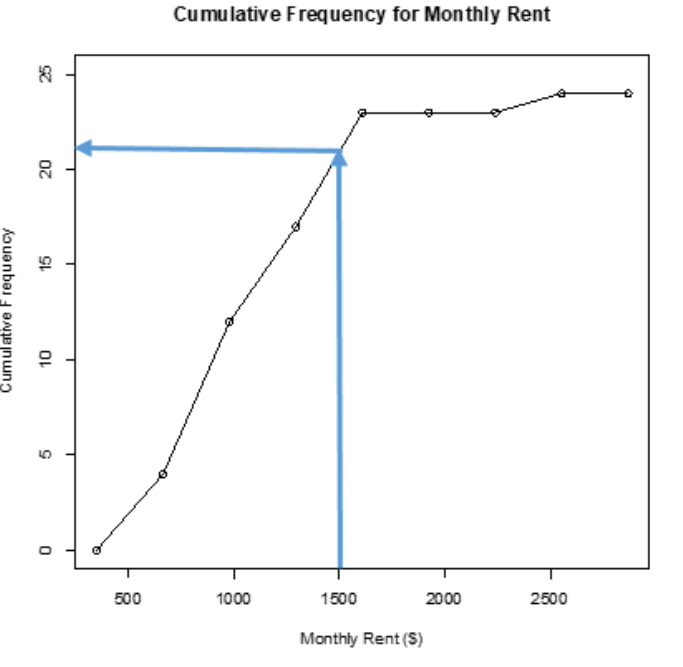
Figure 2-18

If you graph the cumulative relative frequency then you can find out what percentage is below a certain number instead of just the number of people below a certain value.

Using the sample of 35 ages, make an ogive.

46 47 49 25 46 22 42 24 46 40 39 27 25 30 33 27 46 21 29 20 26 25 25 26 35 49 33 26 32 31 39 30 39 29 26

Solution

Excel

Excel will plot an ogive over a histogram as one of its options, but the scale is harder to read.

Type the data in any order into column A and the bins in order in column B as shown below. Then select the Data tab, select Data Analysis, select Histogram, then select OK, see below.

In the dialogue box, click into the Input Range box, then use your mouse and highlight the ages including the label. Then click into the Bin Range box and use your mouse to highlight the bins including the label. Select the box for Labels only if you included the labels in your ranges. You can have your output default to a new worksheet, or select the circle to the left of Output Range, click into the box to the right of Output Range and then select one blank cell on your spreadsheet where you want the top left-hand corner of your table and graph to start. Then check the boxes next to Cumulative Percentage and Chart Output. Then select OK.

Excel produces both a frequency table and a histogram. The table has the frequencies and the cumulative relative frequencies.

Bin	Frequency	Cumulative %
24	4	11.43%
29	12	45.71%
34	6	62.86%
39	4	74.29%
44	2	80.00%
49	7	100.00%
More	0	100.00%

The orange line is the ogive and the vertical axis is on the right side.

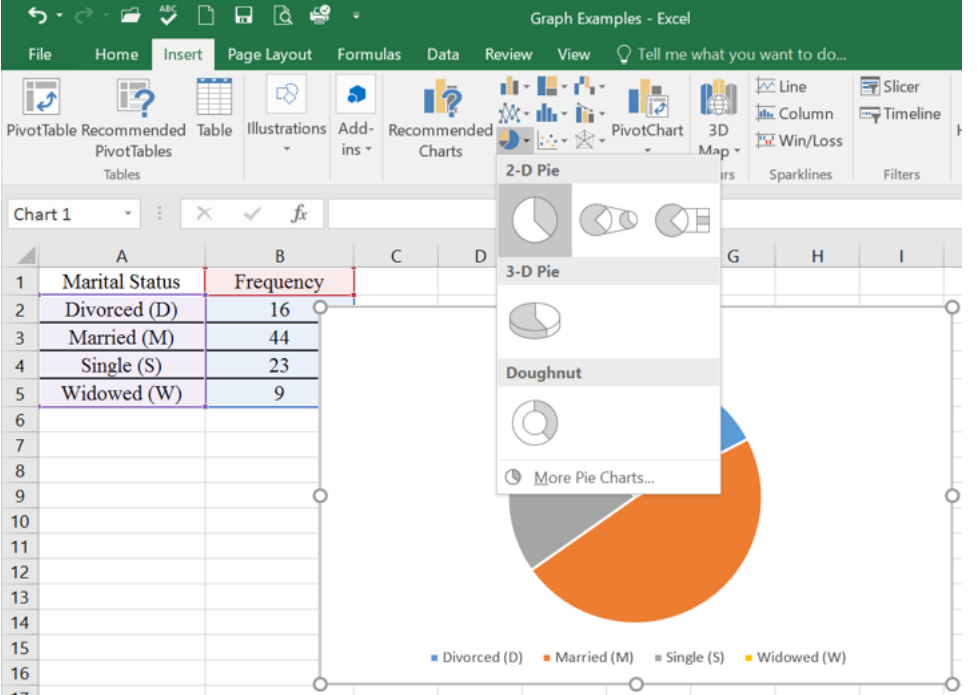
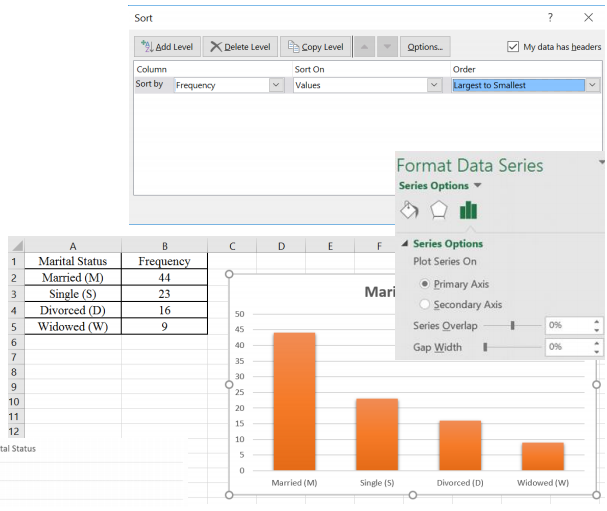
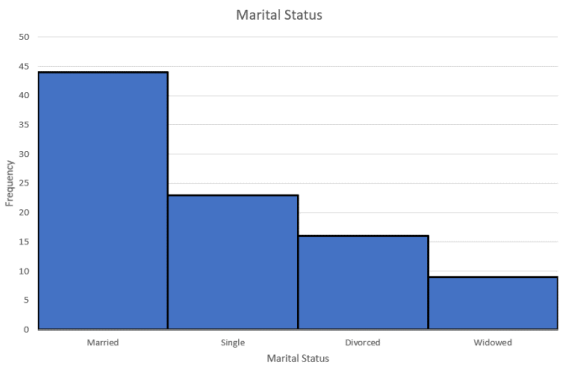
2.3.4 Pie Chart

You cannot make stem-and-leaf plots, histograms, ogives or time series graphs for qualitative data. Instead, we use bar or pie charts for a qualitative variable, which lists the categories and gives either the frequency (count) or the relative frequency (percent) of individual items that fall into each category.

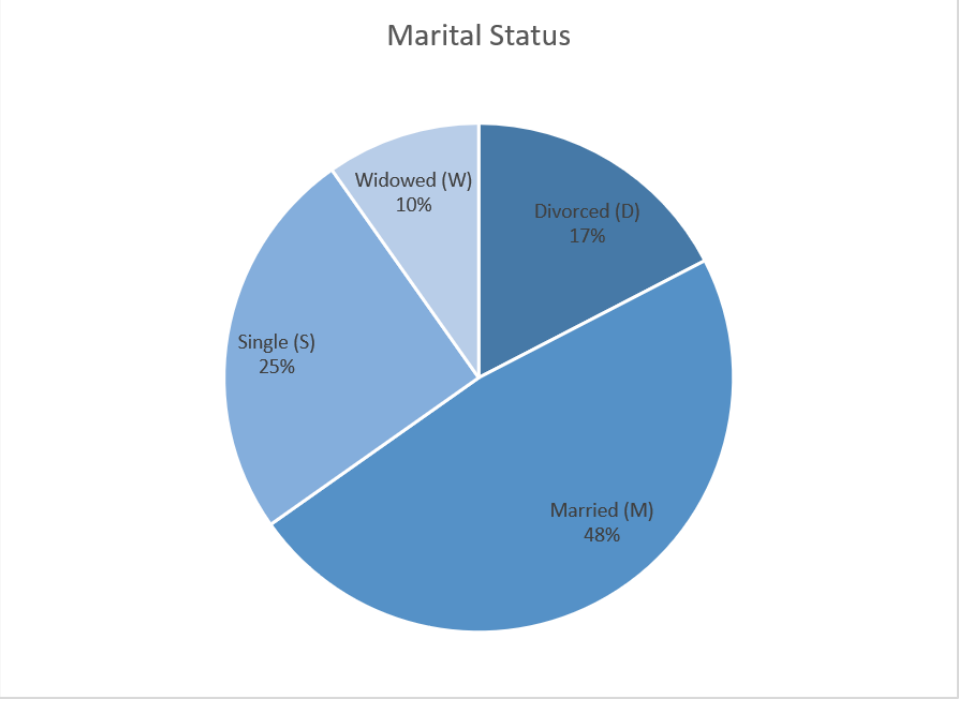
A pie chart or pie graph is a very common and easy-to-construct graph for qualitative data. A pie chart takes a circle and divides the circle into pie shaped wedges that are proportional to the size of the relative frequency. There are 360 degrees in a full circle. Relative frequency is just the percentage as a decimal. To find the angle for each pie wedge, multiply the relative frequency for each category by 360 degrees. Figure 2-19 is an example of a pie chart.

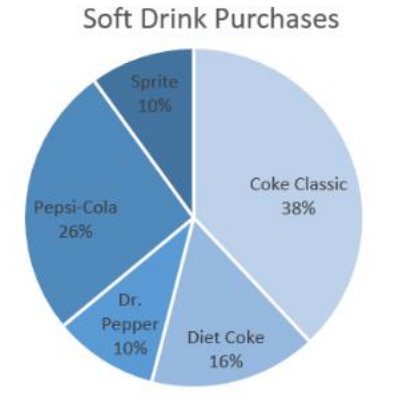
Figure 2-19

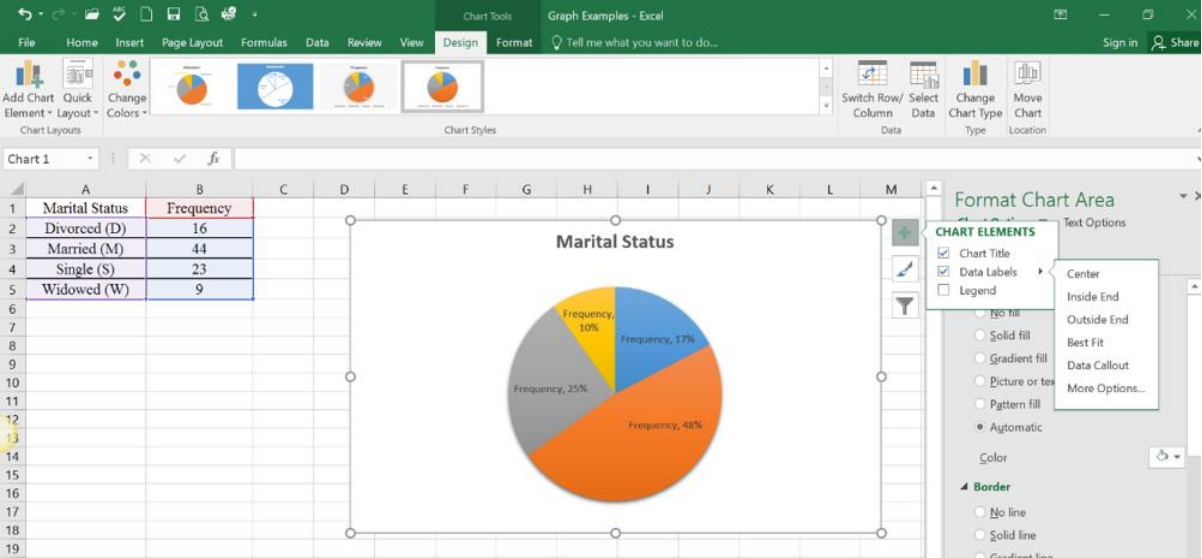
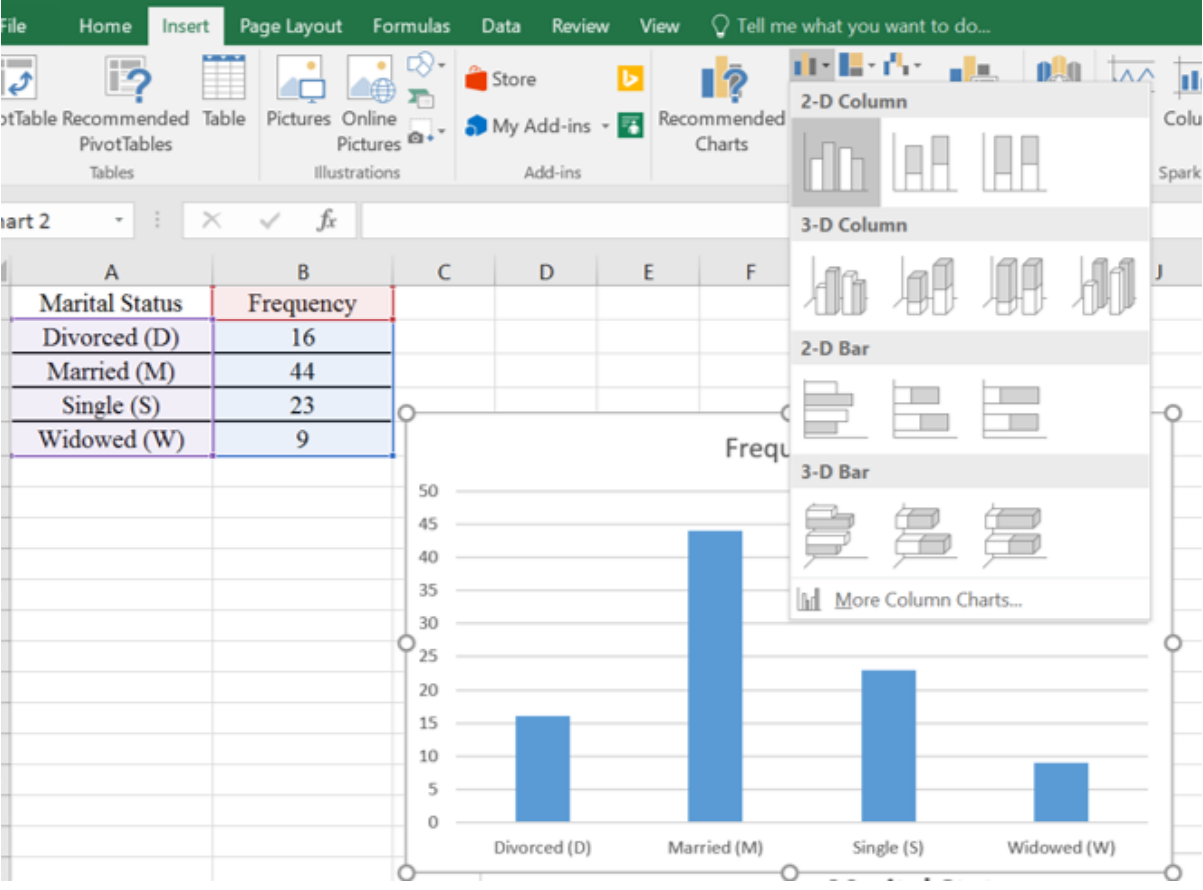
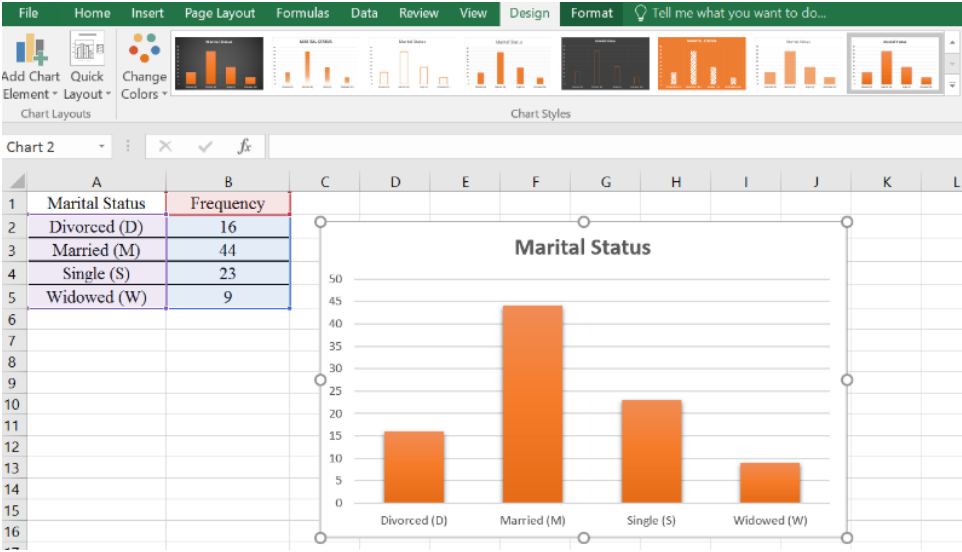
Use Excel to make a pie chart for the following frequency distribution of marital status.

Marital Status Frequency Divorced (D) 16 Married (M) 44 Single (S) 23 Widowed (W) 9

Solution

In Excel, type in the table as it appears, then use your mouse and highlight the entire table. Select the Insert tab, then select the pie graph icon, then select the first option under the 2-D Pie.

Once you have the pie chart you can select the Design window to get a graph to your liking.

It is good practice to include the class label and the percent. The percent should add up to 100%, although with rounding sometimes the sum can be off by 1%.

You can also click on the green plus sign to the right of the graph and add different formatting options, or the paintbrush to change colors.

Here is the finished pie graph.

2.3.5 Bar Graph

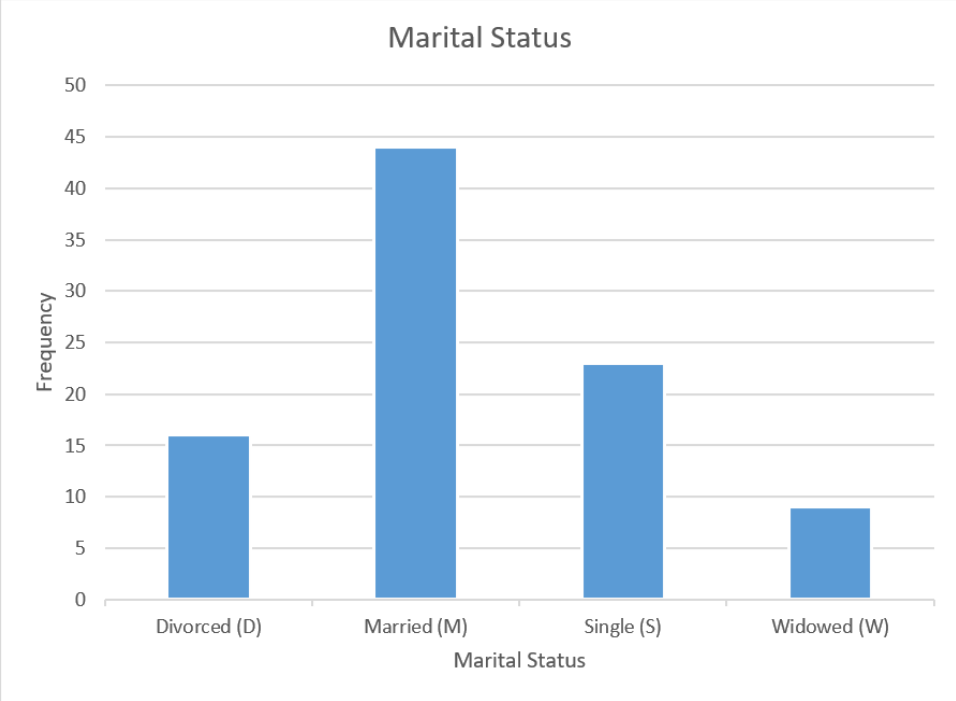
A bar graph (column graph or bar chart) is another graph of a distribution for qualitative data. Bar graphs or charts consist of frequencies on one axis and categories on the other axis. Then you draw rectangles for each category with a height (if frequency is on the vertical axis) or length (if frequency is on the horizontal axis) that is equal to the frequency. All of the rectangles should be the same width, and there should be equally wide gaps between each bar. Figure 2-20 is an example of a bar chart.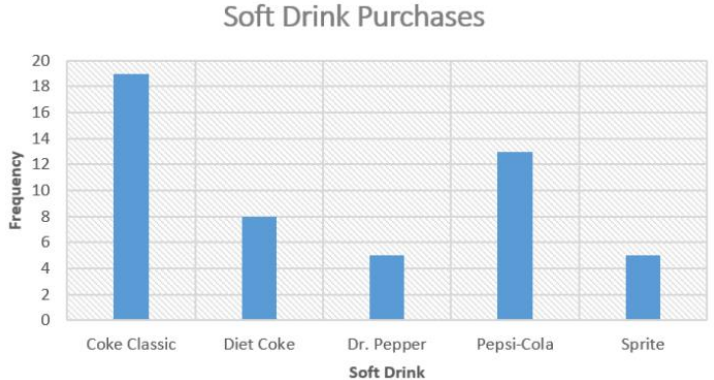

Figure 2-20

Some key features of a bar graph:

Equal spacing on each axis
Bars are the same width
Label each axis and title the graph
Show the scale on the frequency axis
Label the categories on the category axis
The bars do not touch.

You can draw a bar graph with frequency or relative frequency on the vertical axis. The relative frequency is useful when you want to compare two samples with different sample sizes. The relative frequency graph and the frequency graph should look the same, except for the scaling on the frequency axis.

Use Excel to make a bar chart for the following frequency distribution of marital status.

Marital Status Frequency Divorced (D) 16 Married (M) 44 Single (S) 23 Widowed (W) 9

Solution

In Excel, type in the table as it appears, then use your mouse and highlight the entire table.

Similar steps as the pie chart, but this time choose the column graph option we get the following bar graph for marital status.

Then format the graph as needed.

The completed bar graph is below.

Pie charts are useful for comparing sizes of categories. Bar charts show similar information. It really is a personal preference and what information you are trying to address. However, pie charts are best when you only have a few categories and the data can be expressed as a percentage.

The data does not have to be percentages to draw the pie chart, but if a data value can fit into multiple categories, you cannot use a pie chart to display the data. As an example, if you are asking people which is their favorite national park and you ask them to pick their top three choices, then the total number of answers can add up to more than 100% of the people surveyed. Therefore, you cannot use a pie chart to display the favorite national park, but a bar chart would be appropriate.

2.3.6 Pareto Chart

A Pareto (pronounced pə-RAY-toh) chart is a bar graph that starts from the most frequent class to the least frequent class. The advantage of Pareto charts is that you can visually see the more popular answer to the least popular. This is especially useful in business applications, where you want to know what services your customers like the most, what processes result in more injuries, which issues employees find more important, and other type of questions where you are interested in comparing frequency. Figure 2-21 is an example of a Pareto chart.

Pareto

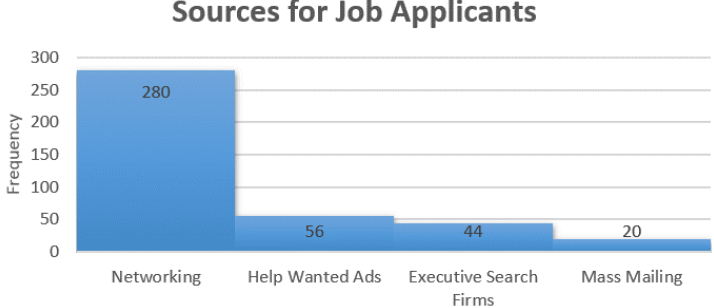
Figure 2-21

Use Excel to make a Pareto chart for the following frequency distribution of marital status.

Marital Status Frequency Divorced (D) 16 Married (M) 44 Single (S) 23 Widowed (W) 9

Solution

In Excel, type in the table as it appears, then use your mouse and highlight the entire table. Highlight the table, then select the Home tab, then select Sort & Filter, then select Custom Sort.

Change the Sort by to Frequency and the Order to Largest to Smallest and click OK.

This will automatically arrange the bars in your bar chart from largest to smallest.

Many Pareto charts will have the bars touching. You can right click on the bars, choose format data series, and then change the Gap Width to zero.

Here is the completed Pareto chart.

There are many other types of graphs used on qualitative data. There are software packages that will create most of them. It depends on your data as to which graph may be best to display the data.

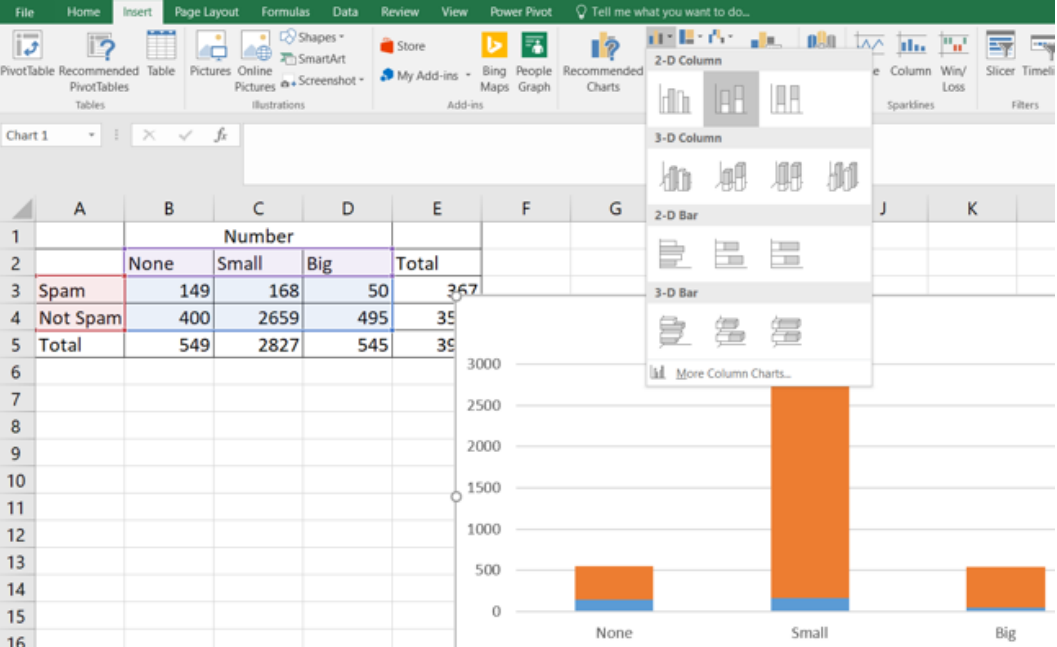
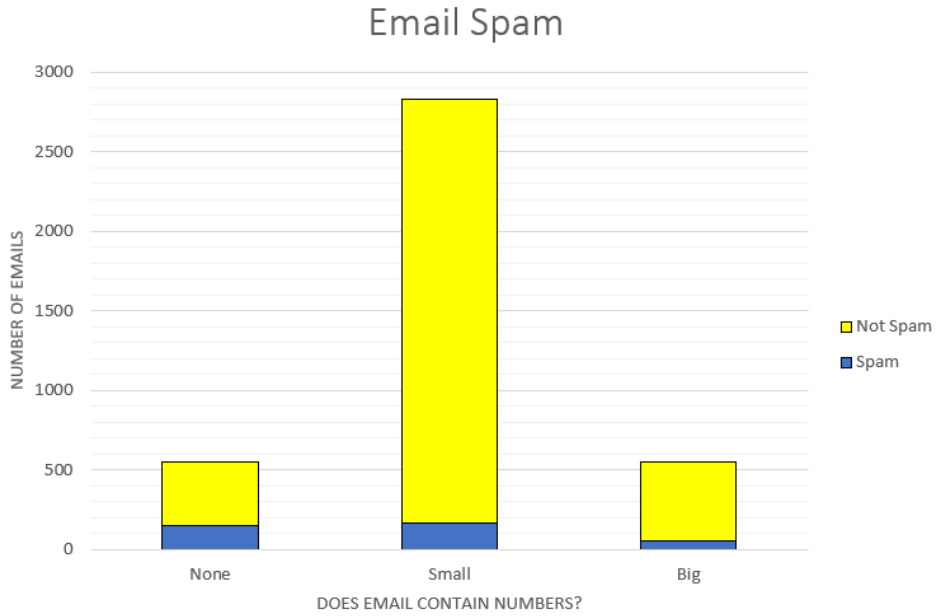
2.3.7 Stacked Column Chart

The next example illustrates one of these types known as a stacked column chart. Stacked column (bar) charts are used when we need to show the ratio between a total and its parts. Each color shows the different series as a part of the same single bar, where the entire bar is used as a total.

In the Wii Fit game, you can do four different types of exercises: yoga, strength, aerobic, and balance. The Wii system keeps track of how many minutes you spend on each of the exercises every day. The following graph is the data for Niko over one-week time-period. Discuss any interpretations you can infer from the graph.

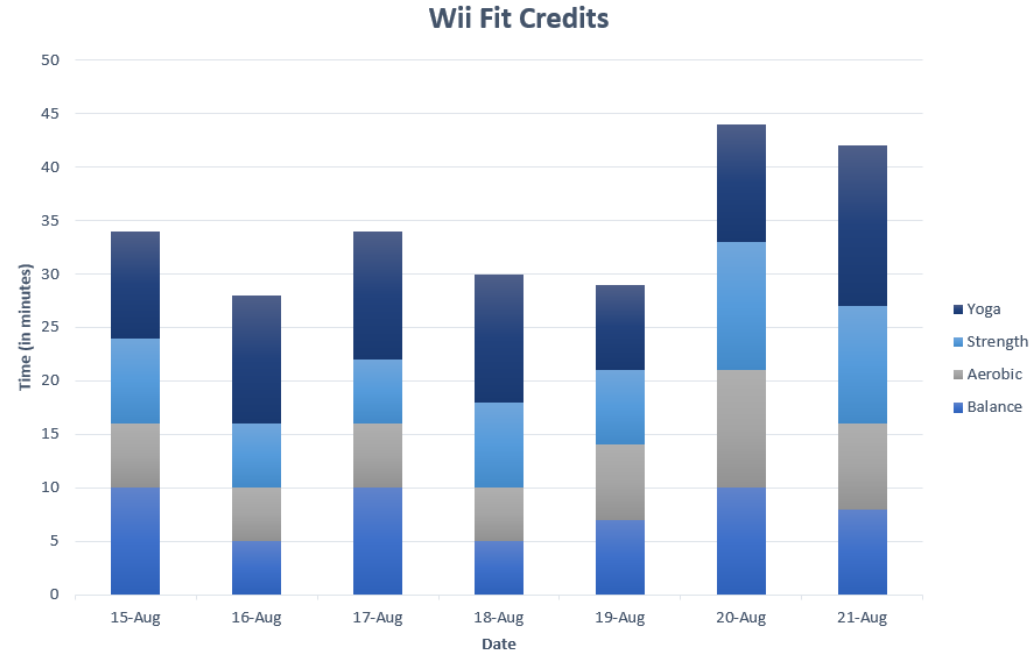
Figure 2-22

Solution

It appears that Niko spends more time on yoga than on any other exercises on any given day. He seems to spend less time on aerobic exercises on a given day. There are several days when the amount of exercise in the different categories is almost equal. The usefulness of a stacked column chart is the ability to compare several different categories over another variable, in this case time. This allows a person to interpret the data with a little more ease.

Data scientists write programming using statistics to filter spam from incoming email messages. By noting specific characteristics of an email, a data scientist may be able to classify some emails as spam or not spam with high accuracy. One of those characteristics is whether the email contains no numbers, small numbers, or big numbers. Make a stacked column chart with the data in the table. Which type of email is more likely to be spam?

Number None Small Big Total Spam 149 168 50 367 Not Spam 400 2659 495 3554 Total 549 2827 545 3921

Example from OpenIntroStatistics.

Solution

Type the summarized table into Excel. Highlight just the inside of the table from the row label, column label and data (do not include the totals or Number label). Select the Insert tab, and then select the 2nd option under the column chart. Add a legend, labels and change colors for clarity.

The completed stacked bar graph is shown in Figure 2-23.

Figure 2-23

Emails with no numbers have a relatively high rate of spam email (149/549 = 0.271) about 27%. On the other hand, less than 10% of email with small numbers (168/2827 = 0.059) or big numbers (50/545 = 0.092) are spam.

2.3.8 Multiple or Side-by-Side Bar Graph

A multiple bar graph, also called a side-by-side bar graph, allows comparisons of several different categories over another variable.

The percentages of people who use certain contraceptives in Central American countries are displayed in the graph below. Use the graph to find the type of contraceptive that is most used in Costa Rica and El Salvador.

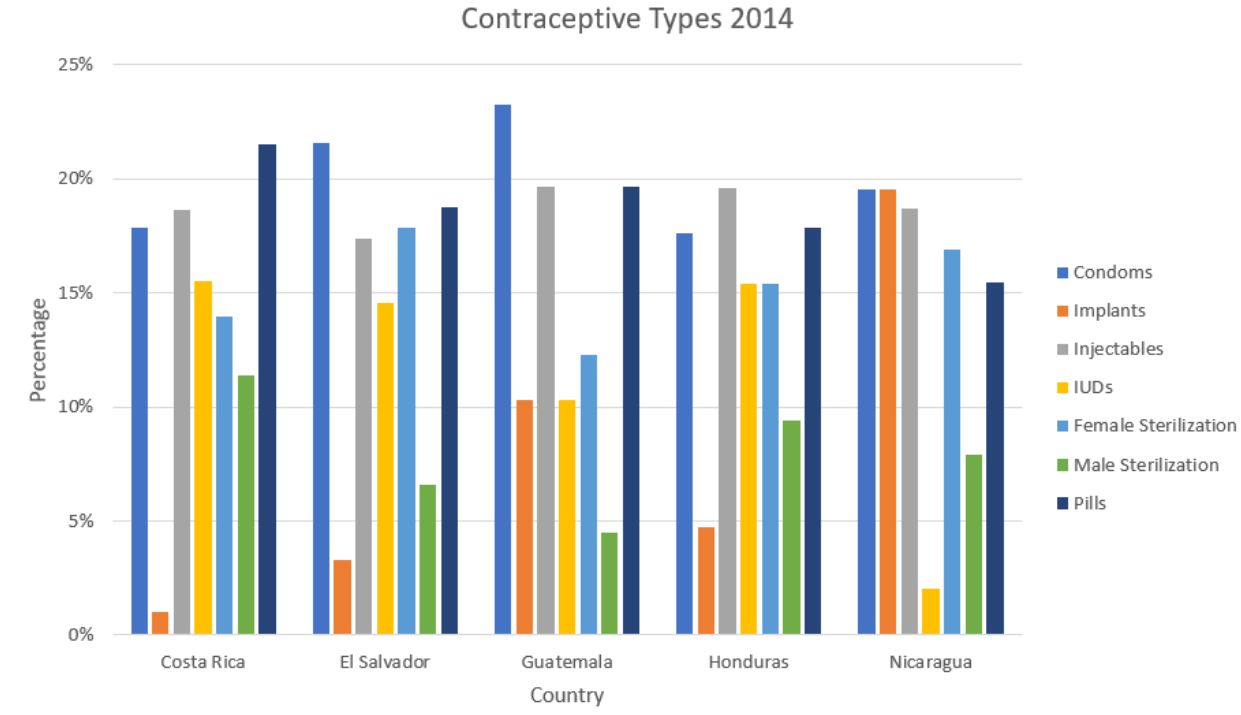
(9/21/2020) Retrieved from https://public.tableau.com/profile/prbdata#!/vizhome/AccesstoContraceptiveMethods/AccesstoContraceptiveMethods

Figure 2-24

Solution

This side-by-side bar graph allows you to quickly see the differences between the countries. For instance, the birth control pill is used most often in Costa Rica, while condoms are most used in El Salvador.

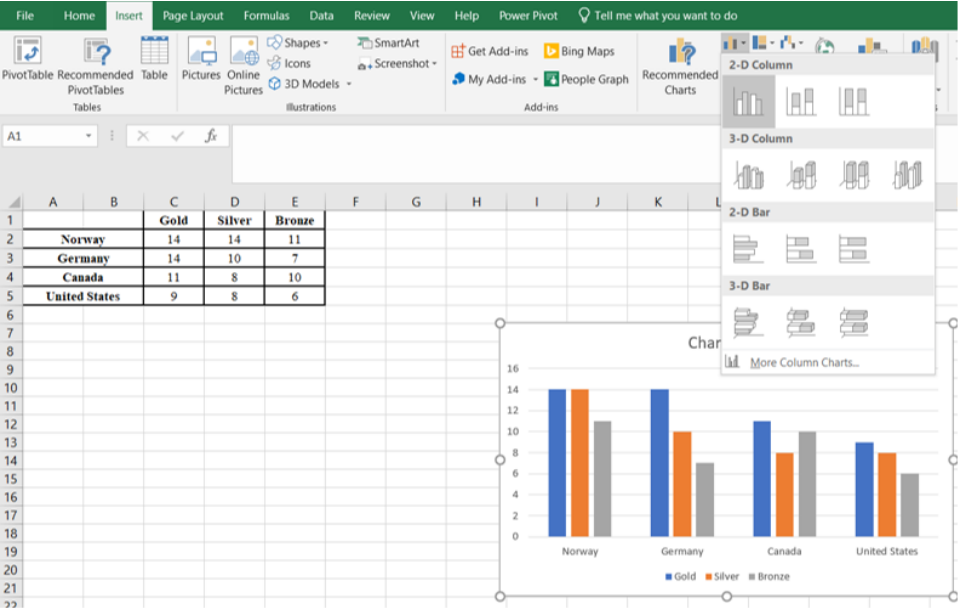
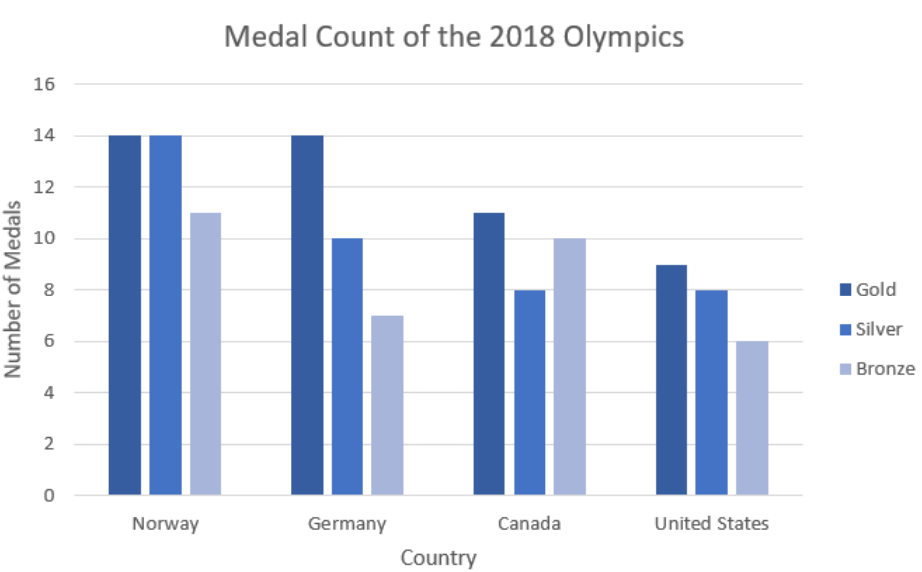
Make a side-by-side bar graph for the following medal count for the 2018 Olympics.

GoldSilverBronzeNorway 14 14 11 Germany 14 10 7 Canada 11 8 10 United States 9 8 6

Solution

Copy the table over to Excel. Highlight the entire table, then use similar steps as the regular bar graph.

Add labels and change the color. The completed graph is shown below.

2.3.9 Time-Series Plot

A time-series plot is a graph showing the data measurements in chronological order, where the data is quantitative data. For example, a time-series plot is used to show profits over the last 5 years. To create a time-series plot, time always goes on the horizontal axis, and the frequency or relative frequency goes on the vertical axis. Then plot the ordered pairs and connect the dots. A time series allows you to see trends over time. Caution: You must realize that the trend may not continue. Just because you see an increase does not mean the increase will continue forever. As an example, prior to 2007, many people noticed that housing prices were increasing. The belief at the time was that housing prices would continue to increase. However, the housing bubble burst in 2007, and many houses lost value during the recession.

The New York Stock Exchange (NYSE) has a website where you can download information on the stock market. Use technology to make a time-series plot.

The daily trading volume for two weeks was downloaded at http://www.nyxdata.com/Data-Products/NYSE-Volume-Summary#summaries.

Trade Date	NYSE Trades	NYSE Volume	NYSE Dollar Volume
2-Nov-17	3,126,422	900,365,416	$35,252,842,833
1-Nov-17	2,951,960	862,960,656	$32,609,257,159
31-Oct-17	2,712,611	944,584,968	$37,697,844,745
30-Oct-17	2,749,134	855,767,500	$33,455,644,270
27-Oct-17	2,816,612	882,117,579	$34,636,857,517
26-Oct-17	2,771,894	866,549,040	$34,105,511,597
25-Oct-17	2,823,272	895,997,132	$36,504,371,518
24-Oct-17	2,369,409	763,566,128	$31,139,796,280
23-Oct-17	2,165,477	745,070,262	$30,216,979,896
20-Oct-17	2,198,245	861,995,044	$37,745,087,429
19-Oct-17	2,211,641	692,171,878	$28,682,027,691
18-Oct-17	2,108,579	669,011,182	$28,642,623,992
17-Oct-17	2,045,857	680,893,022	$28,072,416,838
16-Oct-17	2,078,792	685,406,032	$27,524,409,199
13-Oct-17	2,151,643	757,155,836	$30,624,653,749

Solution

Using Excel, we will make a time series plot for NYSE daily trading volume. Using the Ctrl key highlight just the date column and the NYSE Volume, then select the Insert tab and the first 2-D line graph option.

You can then select different designs.

One can use time-series plots to see when they want to cash out or buy a stock.

The time-series graph shows the behavior of one variable over time and does not reflect other variables that are influencing the trading volume.

2.3.10 Scatter Plot

Sometimes you have two quantitative variables and you want to see if they are related in any way. A scatter plot helps you to see what the relationship may look like. A scatter plot is just a plotting of the ordered pairs.

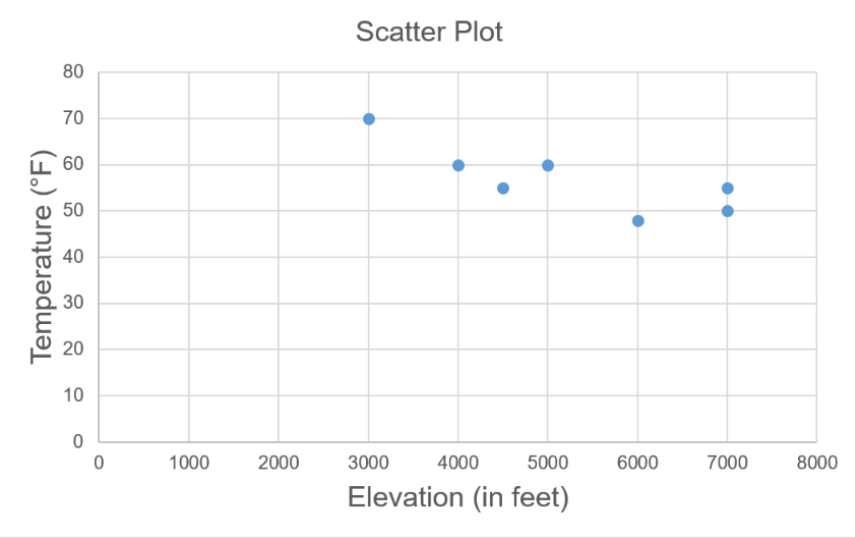
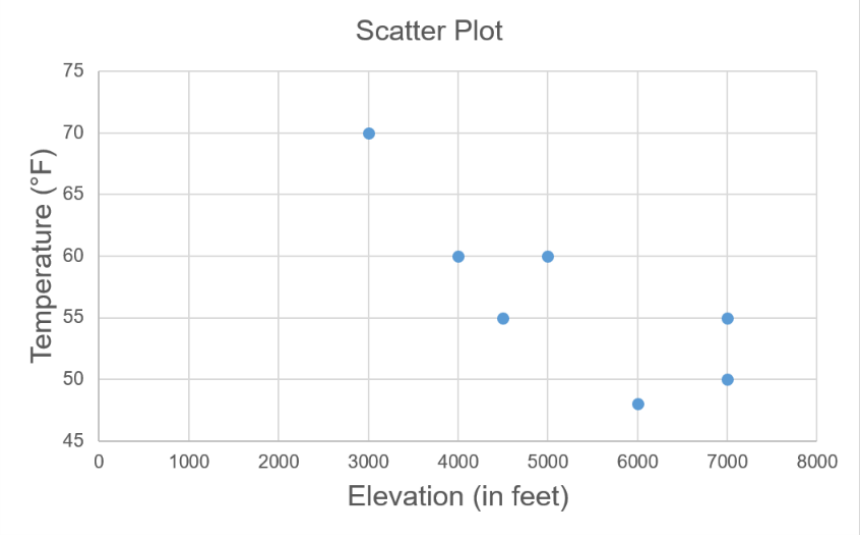
When you see the dots increasing from left to right then there is a positive relationship between the two quantitative variables.
If the dots are decreasing from left to right then there is a negative relationship.
If there is no apparent pattern going up or down, then we say there is no relationship between the two variables.

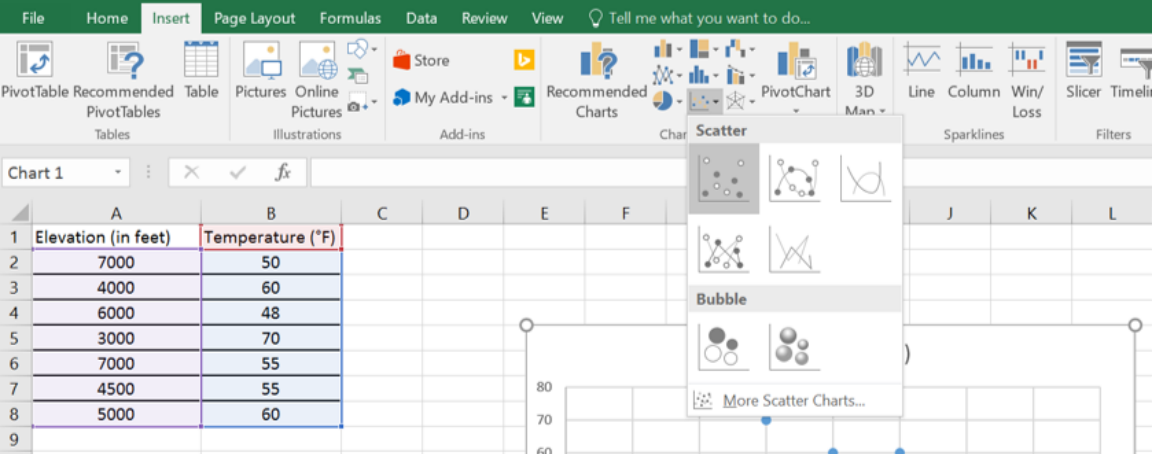
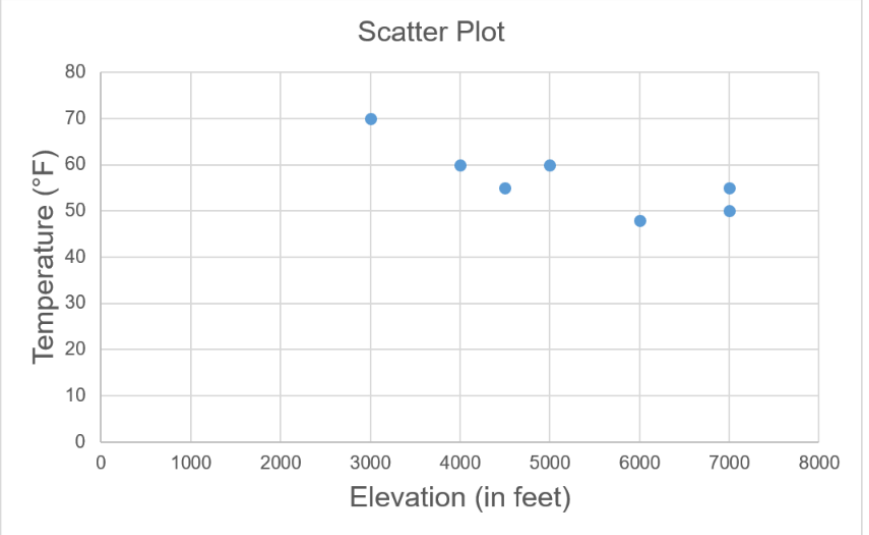
Is there any relationship between elevation and high temperature on a given day? The following data are the high temperatures at various cities on a single day and the elevation of the city.

Make a scatterplot to see what type of relationship exists.

Elevation (in feet) 7000 4000 6000 3000 7000 4500 5000 Temperature (°F) 50 60 48 70 55 55 60

Solution

Excel

Type the data into two columns next to each other. It is important not to have a blank column between the points or Excel may give you an error message. Once you type your data into columns A and B, use your mouse and highlight all the data including the labels. Select the Insert tab, and then select the first box under Scatter.

Add appropriate labels. The completed scatter plot is shown below.

TI-84: First, enter the data into lists 1 and 2. Press [STAT] the first option is already highlighted (1:Edit) so you can either press [ENTER] or 1.Type in the data pressing [ENTER] after each one. For x-y data pairs, enter all x -values in one list. Enter all corresponding y -values in a second list. Press [2nd] [QUIT] to return to the home screen. Make sure you turn off other stat plots or graphs in the y= menu. Press [2^nd] then the [y=] button. Select the first plot. Highlight On and press [Enter] so that On is highlighted. Arrow down to Type and highlight the first option that looks like a scatter plot. Make sure your x and y lists are using L₁ and L₂.

Select Zoom and arrow down to ZoomStat and press [Enter]. You will get the following scatterplot. Select Trace and use your arrow keys to see the values at different points.

TI-89: Press [♦] then [F1] (to get Y=) and clear any equations that are in the y-editor. Open the Stats/List Editor. Press [APPS], select FlashApps then press [ENTER]. Highlight Stats/List Editor then press [ENTER]. Press [ENTER] again to select the main folder. Type in the data pressing [ENTER] after each one. Enter all x-values in one list. Enter all corresponding y-values in a second list. In the Stats/List Editor, select [F2] for the Plots menu. Use cursor keys to highlight 1:Plot Setup. Make sure that the other graphs are turned off by pressing [F4] button to remove the check marks. Under “Plot 1” press [F1] Define.

In the “Plot Type” menu, select “Scatter.” Move the cursor to the “x” space press [2^nd] Var-Link, scroll down to list1, and then press [Enter]. This will put the list name in the dialogue box. Do the same for the y values, but this time choose list2. Press [ENTER] twice and you will be returned to the Plot Setup menu.

Press F5 ZoomData to display the graph.

Press F3 Trace and use the arrow keys to scroll along the different points.

Interpreting the scatter plot.

The graph indicates a linear relationship between temperature and elevation. If you were to hold a pencil up to cover the dots, note that you would see that the dots roughly follow a fat line downhill.

It also appears to be a negative relationship, thus as elevation increases, the temperature decreases.

Figure 2-25

Be careful with the vertical axis of both time-series and scatter plots. If the axis does not start at zero the slope of the line can be exaggerated to show more or less of increase than there really is. This is done in politics and advertising to manipulate the data.

For example, if we change the vertical axis of temperature to go between 45°F and 75°F we get the following scatter plot in Figure 2-26.

We have the same arrangements of dots, but the slope looks much steeper over the 30° range.

Figure 2-26

2.3.11 Misleading Graphs

One thing to be aware of as a consumer, data in the media may be represented in misleading graphs. Misleading graphs not only misrepresent the data, they can lead the reader to false conclusions. There are many ways that graphs can be misleading. One way to mislead is to use picture graphs or 3D graphs that exaggerate differences and should be used with caution. Leaving off units and labels can result in a misleading graph. Another more common example is to rescale or reverse the vertical axis to try to show a large difference between categories. Not starting the vertical axes at zero will show a more dramatic rate of change. Other ways that graphs can be misleading is to change the horizontal axis labels so that they are out of time sequence, using inappropriate graphs, not showing the base population.

What is misleading about the following graph?

An ad for a new diet pill shows the following time-series plot for someone that has lost weight over a 5-month period.

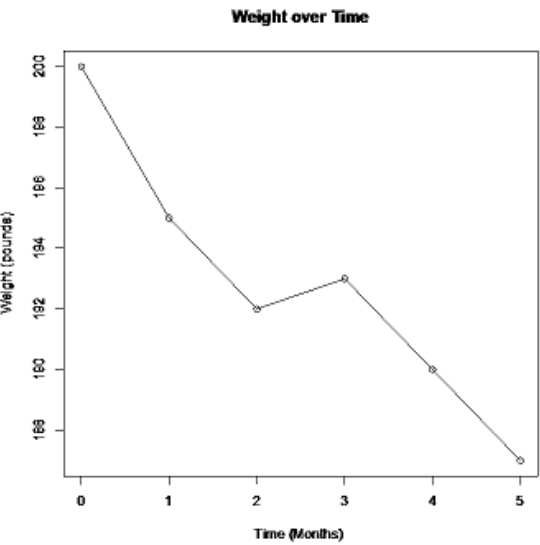
Solution

If you do not start the vertical axis at zero, then a change can look much more dramatic than it really is. Notice the decrease in weight looks much larger in Figure 2-27. The graph in Figure 2-28 has the vertical axis starting at zero. Notice that over the 5 months, the weight appears to be decreasing, however, it does not look like there is a large decrease.

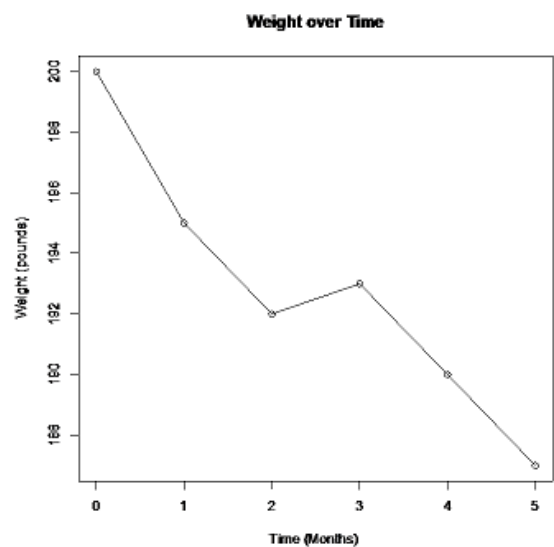
Figure 2-27

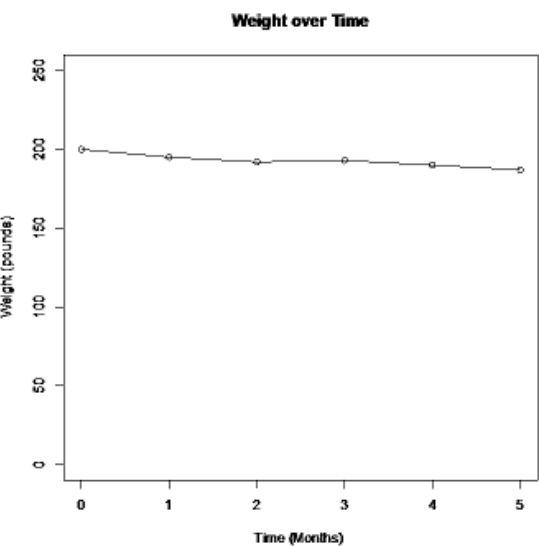
Figure 2-28

What is misleading about the graph in Figure 2-29?

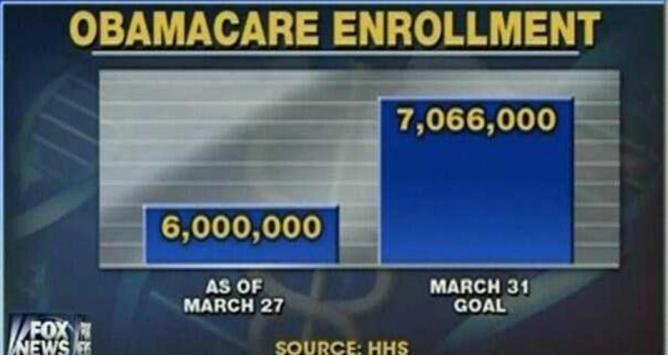
https://www.mediamatters.org/blog/2014/03/31/dishonest-fox-charts-obamacare-enrollment-editi/198679.

Figure 2-29

Solution

The y-axis scale is different for each bar and there are no units on the axis. The first bar has each tic mark as 2 billion, the second bar has each tick as less then 1 billion.

This exaggerates the difference. If they used square scaling as in Figure 2-30, there would not be such an extreme difference between the height of the bars.

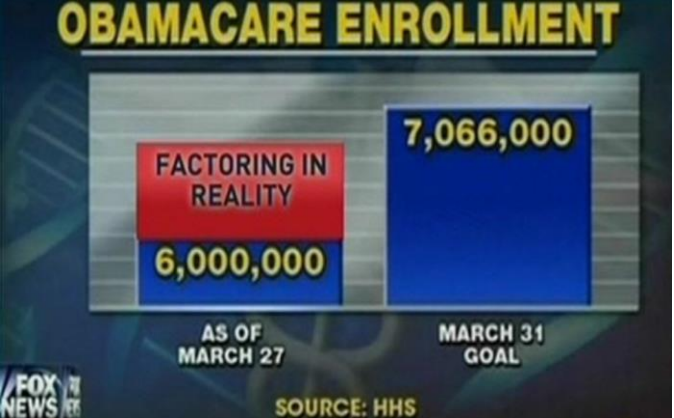
https://www.mediamatters.org/blog/2014/03/31/dishonest-fox-charts-obamacare-enrollment-editi/198679.

Figure 2-30

What is misleading about the graph in Figure 2-31?

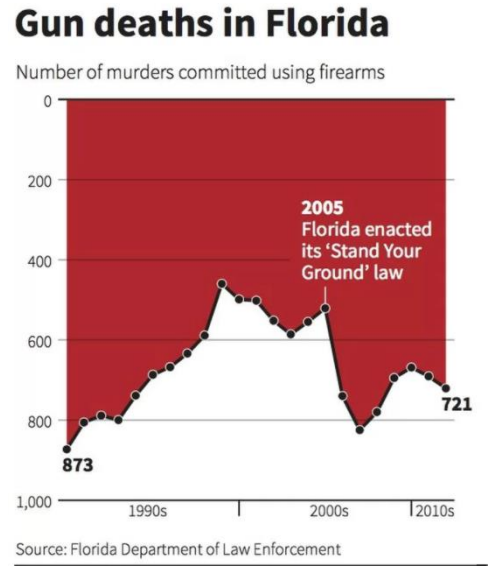
https://www.livescience.com/45083-misleading-gun-death-chart.html

Figure 2-31

Solution

The graph has the y-axis reversed. What looks like an increasing trend line really is decreasing when you correct the y-axis. The red background is also an effect to raise alarm, almost like a curtain of blood.

What is misleading about the graph shown in a Lanacane commercial in May 2012, shown in Figure 2-32?

Retrieved 7/2/2021 from https://youtu.be/I0DapkQ-c1I?t=17

Figure 2-32

Solution

It appears that Lanacane is better than regular hydrocorisone cream at releiving itching. However, note that there are no units or labels to the axis.

What is misleading about the graph published Georgia’s Department of Public Health website in May 2020, shown in Figure 2-33?

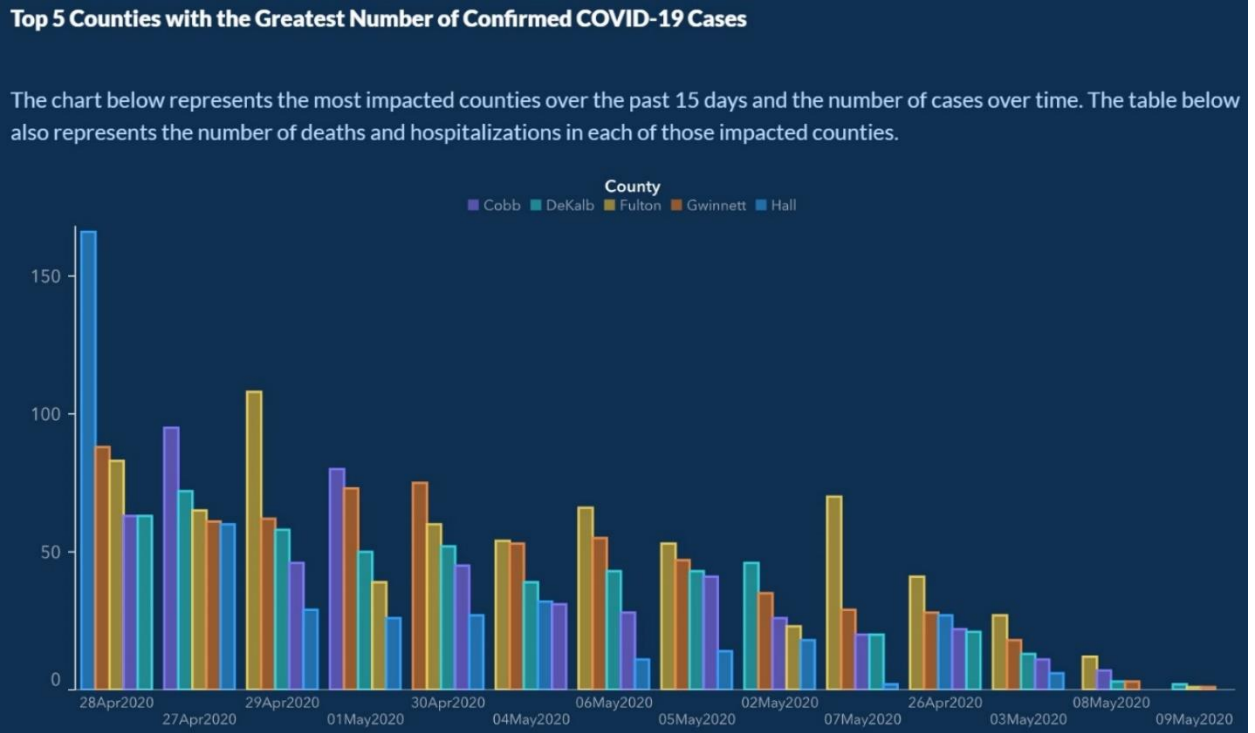
Retrieved 7/3/2021 from https://www.vox.com/covid-19-coronav...ning-reopening Figure 2-33

Solution

There are two misleading items for this graph. The horizontal axis is time, yet the dates are out of sequence starting with April 28, April 27, April 29, May 1, April 30, May 4, May 6, May 5, May 2, May 7, April 26, May 3, May 8, May 9. The first date of April 26 is presented almost at the end of the axis. The graph at first glance would deceive viewers in cases going down over time. A Pareto style chart should never be used for time series data.

The second misleading item is the graph’s title and no label on the y-axis. What does the height of each bar represent? Is the height the number of cases for each county, or is the height the number of deaths and hospitalizations? The website later corrected the graphic as shown in Figure 2-34.

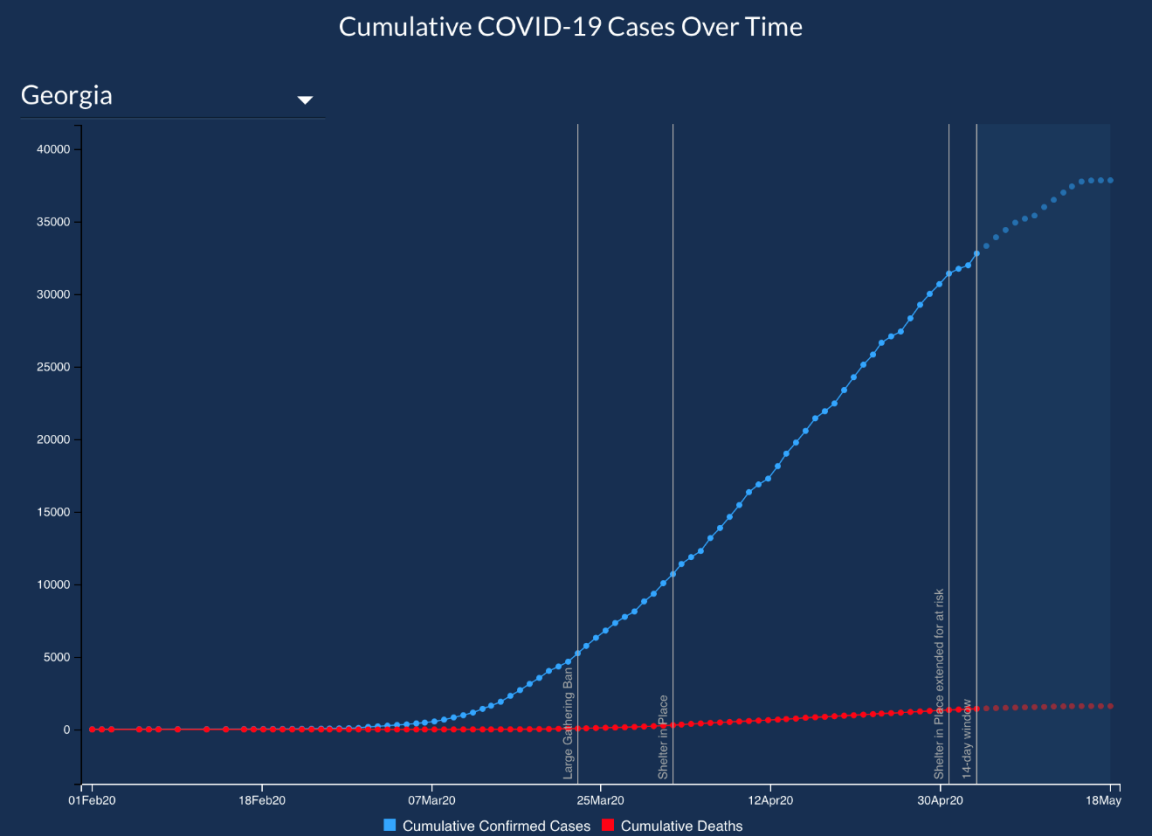
Retrieved 7/3/2021 from https://www.vox.com/covid-19-coronav...ning-reopening Figure 2-34

Large data sets need to be summarized in order to make sense of all the information. The distribution of data can be represented with a table or a graph. It is the role of the researcher or data scientist to make accurate graphical representations that can help make sense of this in the context of the data. Tables and graphs can summarize data, but they alone are insufficient. In the next chapter we will look at describing data numerically.

Search

Text Color

Text Size

Margin Size

Font Type

2.3.1 Stem-and-Leaf Plot

Solution

Solution

Solution

Solution

2.3.2 Histogram

Solution

Solution

Solution

Solution

Solution

Solution

Solution

Solution

Solution

Solution

Solution

Solution

Solution

Solution

Solution

Solution

Solution