6.1: Maximization Applications
- Page ID
- 26544
In this section, you will learn to:
- Recognize the typical form of a linear programing problem
- Formulate maximization linear programming problems
- Graph feasibility regions for maximization linear programming problems
- Determine optimal solutions for maximization linear programming problems.
Application problems in business, economics, and social and life sciences often ask us to make decisions on the basis of certain conditions. The conditions or constraints often take the form of inequalities. In this section, we will begin to formulate, analyze, and solve such problems, at a simple level, to understand the many components of such a problem.
A typical linear programming problem consists of finding an extreme value of a linear function subject to certain constraints. We are either trying to maximize or minimize the value of this linear function, such as to maximize profit or revenue, or to minimize cost. That is why these linear programming problems are classified as maximization or minimization problems, or just optimization problems. The function we are trying to optimize is called an objective function, and the conditions that must be satisfied are called constraints.
A typical example is to maximize profit from producing several products, subject to limitations on materials or resources needed for producing these items; the problem requires us to determine the amount of each item produced. Another type of problem involves scheduling; we need to determine how much time to devote to each of several activities in order to maximize income from (or minimize cost of) these activities, subject to limitations on time and other resources available for each activity.
In this chapter, we will work with problems that involve only two variables, and therefore, can be solved by graphing. In the next chapter, we’ll learn an algorithm to find a solution numerically. That will provide us with a tool to solve problems with more than two variables. At that time, with a little more knowledge about linear programming, we’ll also explore the many ways these techniques are used in business and wide variety of other fields.
We begin by solving a maximization problem.
Niki holds two part-time jobs, Job I and Job II. She never wants to work more than a total of 12 hours a week. She has determined that for every hour she works at Job I, she needs 2 hours of preparation time, and for every hour she works at Job II, she needs one hour of preparation time, and she cannot spend more than 16 hours for preparation.
If Nikki makes $40 an hour at Job I, and $30 an hour at Job II, how many hours should she work per week at each job to maximize her income?
Solution
We start by choosing our variables.
- Let \(x\) = The number of hours per week Niki will work at Job I.
- Let \(y\) = The number of hours per week Niki will work at Job II.
Now we write the objective function. Since Niki gets paid $40 an hour at Job I, and $30 an hour at Job II, her total income I is given by the following equation.
\[I = 40x + 30y \nonumber \]
Our next task is to find the constraints. The second sentence in the problem states, "She never wants to work more than a total of 12 hours a week." This translates into the following constraint:
\[x + y \leq 12 \nonumber \]
The third sentence states, "For every hour she works at Job I, she needs 2 hours of preparation time, and for every hour she works at Job II, she needs one hour of preparation time, and she cannot spend more than 16 hours for preparation." The translation follows.
\[2x + y \leq 16 \nonumber \]
The fact that \(x\) and \(y\) can never be negative is represented by the following two constraints:
\[x \geq 0 \text{, and } y \geq 0 \nonumber. \nonumber \]
Well, good news! We have formulated the problem. We restate it as
\begin{array}{ll}
\textbf { Maximize } & \mathrm{I}=40 \mathrm{x}+30 \mathrm{y} \\
\textbf { Subject to: } & \mathrm{x}+\mathrm{y} \leq 12 \\
& 2 \mathrm{x}+\mathrm{y} \leq 16 \\
& \mathrm{x} \geq 0 ; \mathrm{y} \geq 0
\end{array}
In order to solve the problem, we graph the constraints and shade the region that satisfies all the inequality constraints.
Any appropriate method can be used to graph the lines for the constraints. However often the easiest method is to graph the line by plotting the x-intercept and y-intercept.
The line for a constraint will divide the plane into two region, one of which satisfies the inequality part of the constraint. A test point is used to determine which portion of the plane to shade to satisfy the inequality. Any point on the plane that is not on the line can be used as a test point.
- If the test point satisfies the inequality, then the region of the plane that satisfies the inequality is the region that contains the test point.
- If the test point does not satisfy the inequality, then the region that satisfies the inequality lies on the opposite side of the line from the test point.
In the graph below, after the lines representing the constraints were graphed using an appropriate method from Chapter 1, the point (0,0) was used as a test point to determine that
- (0,0) satisfies the constraint \(x + y \leq 12\) because \(0 + 0 < 12\)
- (0,0) satisfies the constraint \(2x + y \leq 16\) because \(2(0) + 0 < 16\)
Therefore, in this example, we shade the region that is below and to the left of both constraint lines, but also above the x axis and to the right of the y axis, in order to further satisfy the constraints \(x \geq 0\) and \(y \geq 0\).
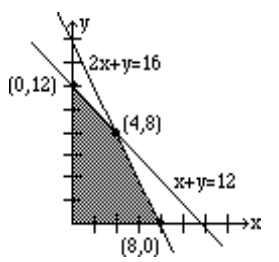
The shaded region where all conditions are satisfied is called the feasibility region or the feasibility polygon.
The Fundamental Theorem of Linear Programming states that the maximum (or minimum) value of the objective function always takes place at the vertices of the feasibility region.
Therefore, we will identify all the vertices (corner points) of the feasibility region. We call these points critical points. They are listed as (0, 0), (0, 12), (4, 8), (8, 0). To maximize Niki's income, we will substitute these points in the objective function to see which point gives us the highest income per week. We list the results below.
| Critical Points | Income |
|---|---|
| (0, 0) | 40(0) + 30(0) = $0 |
| (0, 12) | 40(0) + 30(12) = $360 |
| (4, 8) | 40(4) + 30(8) = $400 |
| (8, 0) | 40(8) + 30(0) = $320 |
Clearly, the point (4, 8) gives the most profit: $400.
Therefore, we conclude that Niki should work 4 hours at Job I, and 8 hours at Job II.
A factory manufactures two types of gadgets, regular and premium. Each gadget requires the use of two operations, assembly and finishing, and there are at most 12 hours available for each operation. A regular gadget requires 1 hour of assembly and 2 hours of finishing, while a premium gadget needs 2 hours of assembly and 1 hour of finishing. Due to other restrictions, the company can make at most 7 gadgets a day. If a profit of $20 is realized for each regular gadget and $30 for a premium gadget, how many of each should be manufactured to maximize profit?
Solution
We choose our variables.
- Let \(x\) = The number of regular gadgets manufactured each day.
- and \(y\) = The number of premium gadgets manufactured each day.
The objective function is
\[P = 20x + 30y \nonumber \]
We now write the constraints. The fourth sentence states that the company can make at most 7 gadgets a day. This translates as
\[x + y \leq 7 \nonumber \]
Since the regular gadget requires one hour of assembly and the premium gadget requires two hours of assembly, and there are at most 12 hours available for this operation, we get
\[x + 2y \leq 12 \nonumber \]
Similarly, the regular gadget requires two hours of finishing and the premium gadget one hour. Again, there are at most 12 hours available for finishing. This gives us the following constraint.
\[2x + y \leq 12 \nonumber \]
The fact that \(x\) and \(y\) can never be negative is represented by the following two constraints:
\[x \geq 0 \text{, and } y \geq 0 \nonumber. \nonumber \]
We have formulated the problem as follows:
\[\begin{array}{ll}
\textbf { Maximize } & \mathrm{P}=20 \mathrm{x}+30 \mathrm{y} \\
\textbf { Subject to: } & \mathrm{x}+\mathrm{y} \leq 7 \\
& \mathrm{x}+2\mathrm{y} \leq 12 \\
& 2\mathrm{x} +\mathrm{y} \leq 12 \\
& \mathrm{x} \geq 0 ; \mathrm{y} \geq 0
\end{array} \nonumber \]
In order to solve the problem, we next graph the constraints and feasibility region.
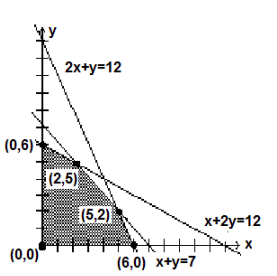
Again, we have shaded the feasibility region, where all constraints are satisfied.
Since the extreme value of the objective function always takes place at the vertices of the feasibility region, we identify all the critical points. They are listed as (0, 0), (0, 6), (2, 5), (5, 2), and (6, 0). To maximize profit, we will substitute these points in the objective function to see which point gives us the maximum profit each day. The results are listed below.
| Critical Point | Income |
|---|---|
| (0, 0) | 20(0) + 30(0) = $0 |
(0, 6) |
20(0) + 30(6) = $180 |
(2, 5) |
20(2) + 30(5) = $190 |
(5, 2) |
20(5) + 30(2) = $160 |
| (6,0) | 20(6) + 30(0) = $120 |
The point (2, 5) gives the most profit, and that profit is $190.
Therefore, we conclude that we should manufacture 2 regular gadgets and 5 premium gadgets daily to obtain the maximum profit of $190.
So far we have focused on “standard maximization problems” in which
- The objective function is to be maximized
- All constraints are of the form \(ax + by \leq c\)
- All variables are constrained to by non-negative (\(x ≥ 0\), \(y ≥ 0\))
We will next consider an example where that is not the case. Our next problem is said to have “mixed constraints”, since some of the inequality constraints are of the form \(ax + by ≤ c\) and some are of the form \(ax + by ≥ c\). The non-negativity constraints are still an important requirement in any linear program.
Solve the following maximization problem graphically.
\[\begin{array}{ll}
\textbf { Maximize } & \mathrm{P}=10 \mathrm{x}+15 \mathrm{y} \\
\textbf { Subject to: } & \mathrm{x}+\mathrm{y} \geq 1 \\
& \mathrm{x}+2\mathrm{y} \leq 6 \\
& 2\mathrm{x} +\mathrm{y} \leq 6 \\
& \mathrm{x} \geq 0 ; \mathrm{y} \geq 0
\end{array} \nonumber \]
Solution
The graph is shown below.
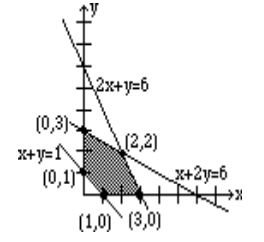
The five critical points are listed in the above figure. The reader should observe that the first constraint \(x + y ≥ 1\) requires that the feasibility region must be bounded below by the line \(x + y =1\); the test point (0,0) does not satisfy \(x + y ≥ 1\), so we shade the region on the opposite side of the line from test point (0,0).
| Critical point | Income |
|---|---|
| (1, 0) | 10(1) + 15(0) = $10 |
| (3, 0) | 10(3) + 15(0) = $30 |
| (2, 2) | 10(2) + 15(2) = $50 |
| (0, 3) | 10(0) + 15(3) = $45 |
| (0,1) | 10(0) + 15(1) = $15 |
Clearly, the point (2, 2) maximizes the objective function to a maximum value of 50.
It is important to observe that that if the point (0,0) lies on the line for a constraint, then (0,0) could not be used as a test point. We would need to select any other point we want that does not lie on the line to use as a test point in that situation.
Finally, we address an important question. Is it possible to determine the point that gives the maximum value without calculating the value at each critical point?
The answer is yes.
For example \(\PageIndex{2}\), we substituted the points (0, 0), (0, 6), (2, 5), (5, 2), and (6, 0), in the objective function \(P = 20x + 30y\), and we got the values $0, $180, $190, $160, $120, respectively.
Sometimes that is not the most efficient way of finding the optimum solution. Instead we could find the optimal value by also graphing the objective function.
To determine the largest \(P\), we graph \(P = 20x + 30y\) for any value \(P\) of our choice. Let us say, we choose \(P = 60\). We graph \(20x + 30y = 60\).
Now we move the line parallel to itself, that is, keeping the same slope at all times. Since we are moving the line parallel to itself, the slope is kept the same, and the only thing that is changing is the P. As we move away from the origin, the value of P increases. The largest possible value of P is realized when the line touches the last corner point of the feasibility region.
The figure below shows the movements of the line, and the optimum solution is achieved at the point (2, 5). In maximization problems, as the line is being moved away from the origin, this optimum point is the farthest critical point.
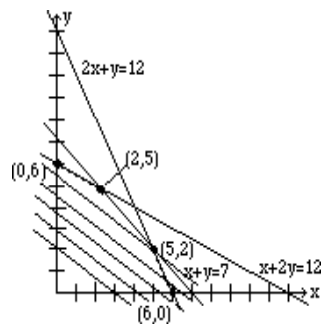
We summarize:
The Maximization Linear Programming Problems
- Write the objective function.
- Write the constraints.
- For the standard maximization linear programming problems, constraints are of the form: \(ax + by ≤ c\)
- Since the variables are non-negative, we include the constraints: \(x ≥ 0\); \(y ≥ 0\).
- Graph the constraints.
- Shade the feasibility region.
- Find the corner points.
- Determine the corner point that gives the maximum value.
- This is done by finding the value of the objective function at each corner point.
- This can also be done by moving the line associated with the objective function.


